F_n が n の倍数であるなら, n は 1 であるか, さもなくば 5 または 12 の倍数である
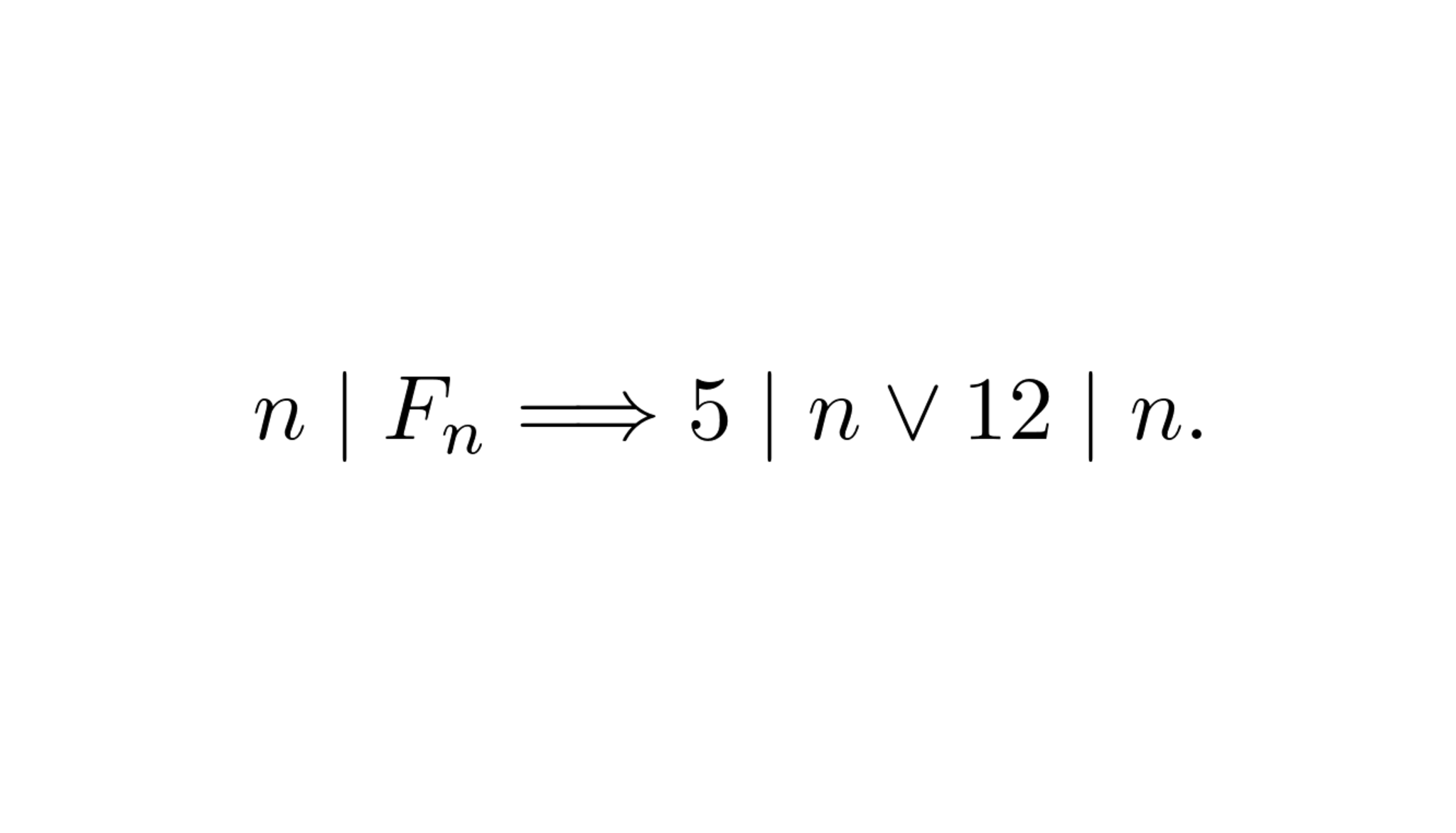 20210817
20210817
前提知識 : Fibonacci 数列, 加法定理, Euclid の互除法, 有限体, Fermat の小定理
Fibonacci 数列 :
https://mathlog.info/articles/191
加法定理 :
https://mathlog.info/articles/320
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
基本性質
先ず最大公約数についての命題から始める.
任意の正整数$n$に対して, $\gcd(F_{n+1},F_n)=1$が成りたつ.
漸化式$F_{n+1}=F_n+F_{n-1}$から
$$
\begin{align}
\gcd(F_{n+1},F_n)=\gcd(F_{n-1},F_n)=\gcd(F_n,F_{n-1})
\end{align}
$$が成りたつため, 再帰的に
$$
\begin{align}
\gcd(F_{n+1},F_n),\ \gcd(F_n,F_{n-1}),\ \ldots,\ \gcd(F_2,F_1)
\end{align}
$$は全て等しく, その値は$1$である. $\quad\Box$
Fibonacci 数の加法定理とは, あらゆる整数$m,n$について
$$
\begin{align}
F_{m+n}=F_mF_{n+1}+F_{m-1}F_n
\end{align}
$$という等式が成立することを主張するものであった. この等式を$F_m$の視点から観るに, $F_{m+n}$は自身の倍数$F_mF_{n+1}$と, 自身に互いに素なる整数と$F_n$の積$F_{m-1}F_n$との和として表現されており, 対$(F_{m+n},F_m)$の全ての公約数は$(F_n,F_m)$にも移る. また逆に, 対$(F_n,F_m)$の公約数は必ず$(F_{m+n},F_m)$の公約数にもなるようである. これは, 整数の割り算を表す等式
$$
\begin{align}
a=bq+r\quad(0\leqslant r< b)
\end{align}
$$において対$(a,b)$と対$(b,r)$の公約数の全体が相等しくなることに類似し, 互除法と同様なる議論を組みたてることができる.
任意の正整数$m,n$に対して, $\gcd(F_m,F_n)=F_{\gcd(m,n)}$が成りたつ.
先ず, 加法定理
$$
\begin{align}
F_{m+n}=F_mF_{n+1}+F_{m-1}F_n
\end{align}
$$において$\gcd(F_m,F_{m-1})=1$であることを用いて
$$
\begin{align}
\gcd(F_{m+n},F_m)=\gcd(F_n,F_m)
\end{align}
$$の成立が確かめられる. $m>n$なる正整数の対$(m,n)$に対して互除法の操作を実行して
$$
\begin{align}
m&=nq_1+r_1\quad(0< r_1< n),\\
n&=r_1q_2+r_2\quad(0< r_2< r_1),\\
&\quad\!\!\!\vdots\\
q_{\ell-1}&=r_{\ell-1}q_\ell+r_\ell\quad(0< r_\ell< r_{\ell-1}),\\
q_\ell&=r_\ell q_{\ell+1}
\end{align}
$$なる除算の列を得たとすると, 先の最大公約数の等式を繰りかえし適用することによって
$$
\begin{align}
\gcd(F_m,F_n)=\gcd(F_{r_1},F_n)=\gcd(F_n,F_{r_1})=\cdots=\gcd(F_{q_\ell},F_{r_\ell})
\end{align}
$$と変形することができ, 最大公約数の等式を再び用いれば
$$
\begin{align}
\gcd(F_{q_\ell},F_{r_\ell})=\gcd(F_{q_{\ell+1}r_\ell},F_{r_\ell})=\gcd(F_{(q_{\ell+1}-1)r_\ell},F_{r_\ell})=\cdots=\gcd(F_{r_{\ell}},F_{r_\ell})=F_{r_\ell}
\end{align}
$$と$\gcd$を外すことができる. $r_\ell$は$\gcd(m,n)$に等しいのであったから, 上記と合わせて
$$
\begin{align}
\gcd(F_m,F_n)=F_{r_\ell}=F_{\gcd(m,n)}
\end{align}
$$が導かれる. また$m< n$の場合は$(m,n)$に関する対称性から直ちに得られ, 残る$m=n$の場合には等式は自明であるため, あらゆる$(m,n)$について証明が完了した. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$p$の倍数
この節では$p$は素数を表すと約束し, 数列$(F_n)_{n>0}$における$p$の倍数の探索のため$p$を法として計算する. 詰まり, 有限体$\mathbb{F}_p=\mathbb{Z}/p\mathbb{Z}$あるいはその拡大系を全体として考察を進めてゆく.
数列$(F_n)$の一般項は, $\phi$と$\bar{\phi}$をそれぞれ黄金比と共役黄金比, 即ち二次方程式$x^2=x+1$の大小二解として
$$
\begin{align}
F_n=\frac{\phi^n-\bar{\phi}^n}{\sqrt{5}}=\frac{\sqrt{5}}{5}\left(\phi^n-\bar{\phi}^n\right)
\end{align}
$$という式によって表現することができるのであった. これに基づき, 有限体に$\sqrt{5}$に対応する概念を導入することによって, $p$の倍数であるような Fibonacci 数を第$p$項の付近で見つけることができる.
任意の$5$でない奇素数$p$について, $F_{p-1}$と$F_{p+1}$の内何れかは$p$の倍数である. また, $5$は$F_5$を割りきる.
$5$については$F_5=5$から明白である.
$p\neq5$で, かつ方程式$X^2-5=0$が$\mathbb{F}_p$に根を持つとき, その解の一つを取り$r$と置いて
$$
\begin{align}
f_n=r^{-1}\left((2^{-1}(1+r))^n-(2^{-1}(1-r))^n\right)\in\mathbb{F}_p
\end{align}
$$により剰余列$(f_n)_{n>0}$を定義すると, $f_n$は$F_n$を法${\rm mod}.p$によって還元したものに等しくなる. Fermat の小定理から
$$
\begin{align}
(2^{-1}(1+r))^{p-1}=1=(2^{-1}(1-r))^{p-1}
\end{align}
$$であるため, $f_{p-1}=0$が成りたち, 故に整数$F_{p-1}$は$p$の倍数である.
その他の場合には, $\mathbb{F}_p$に不定元$X$を付加して$X^2-5=0$が成立するようにした拡大体$L=\mathbb{F}_p[X]/(X^2-5)$において
$$
\begin{align}
f'_n=(5^{-1}t)\left((2^{-1}(1+t))^n-(2^{-1}(1-t))^n\right)\in L
\end{align}
$$により剰余列$(f'_n)_{n>0}$を定義すると, $f'_n$は$F_n$を${\rm mod}.p$と${\rm mod}.(X^2-5)$の両方によって還元したものに等しい. $L$の元を$p$乗する写像が加法と乗法を保つことから, $\varphi=2^{-1}(1+t), $$\bar\varphi=2^{-1}(1-t)$と書けば
$$
\begin{align}
&(\varphi^p)^2-\varphi^p-1=(\varphi^2-\varphi-1)^p=0,\\
&(\bar\varphi^p)^2-\bar\varphi^p-1=(\bar\varphi^2-\bar\varphi-1)^p=0
\end{align}
$$が成りたつため, $\varphi,\bar\varphi,\varphi^p,\bar\varphi^p$は全て同一の二次方程式$x^2-x-1=0$の根である. 所が, $L$の元を$p$乗する写像の不動点は方程式$x^p-x=0$の$p$個の解, 即ち$\mathbb{F}_p$の元に限られるため, $\varphi^p=\bar\varphi$かつ$\bar\varphi^p=\varphi$であり
$$
\begin{align}
\varphi^{p+1}=\varphi\bar\varphi=\bar\varphi^{p+1}
\end{align}
$$
の両辺は等しい. ここから$f'_{p+1}=0$が成りたつことが判り, 故に整数$F_{p+1}$は$p$の倍数である.
以上で命題の証明が完了した. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
主定理
ある正整数$n$に対して$F_n$が$n$の倍数であるならば, $n$は$1$と$5$の何れかであるか, 然もなくば$12$または$25$の正倍数である.
$n\mid F_n$なる関係が成立していることを仮定して$n$に関する必要性を導く. $n=1$に対して$1\mid F_1$が成立することは明白である. $n>1$のとき$n$は素因子を有するが, 若し$n$の最小なる素因子$p$が$2$でも$5$でもないとすれば, ある$\epsilon\in\{1,-1\}$を以て
$$
\begin{align}
p\mid\gcd(F_n,F_{p+\epsilon})=F_{\gcd(n,p+\epsilon)}
\end{align}
$$なる関係式の成立を得られる. $\epsilon\in\{1,-1\}$および$p$の最小性から$\gcd(n,p+\epsilon)=1$となるため, 上式は$p\mid F_1=1$を示すはずである. 所が$p$は素数であったから, これは不合理であり, $p$は$2$または$5$であらなければ成らない.
$p=2$のとき,
$p$の定義から$2\mid n$,
$n\mid F_n$から$2\mid F_n$,
数列$(F_n)$の性質から$3\mid n$,
$n\mid F_n$から$3\mid F_n$,
数列$(F_n)$の性質から$4\mid n$,
$n\mid F_n$から$4\mid F_n$,
数列$(F_n)$の性質から$6\mid n$,
$n\mid F_n$から$6\mid F_n$,
数列$(F_n)$の性質から$12\mid n$,
$n\mid F_n$から$12\mid F_n$,
数列$(F_n)$の性質から$12\mid n$
...
と云うことができるため, 結局$12\mid n$が少なくとも必要な条件である.
$p=5$かつ$n\neq5$のとき, $n/5$の最小なる素因子$q\geqslant5$が$5$でないとすれば, 先と全く同様にして$q\mid F_{\gcd(n,q+\epsilon)}$から$q\mid F_5=5$なる不合理な関係を導くことができるため$q=5$が必要であり, 従って$n$が$25$の倍数であると言える.
以上で命題の証明が完了した. $\quad\Box$
更に, $25$の倍数の中でも$5$の冪$5^e$については下に示すように充分性も成立し, Lucas 数との関係から容易に確かめることが可能である. 尚, $12$および$25$の正倍数についての充分性は何れも成りたたず, たとえば$n=50$のときと$n=84$のときには
$$
\begin{align}
&\frac{\,F_{50}\,}{\,50\,}=\frac{\,(F_{25}/25)L_{25}\,}{\,2\,}\downarrow,\\
&\frac{F_{84}}{84}=\frac{(L_{42}/3)(L_{21}/4)F_{21}}{7}\downarrow
\end{align}
$$で右辺は既約である.
任意の正の整数$n$に対して, $n$が$5$の冪であるならば, $F_n$は$n$の倍数である.
あらゆる非負整数$e$について$5^e\mid F_{5^e}$が成立すること再帰的に証明する. 初期命題として, $e=0$のときの$1\mid F_1$は明白である.
扨て, ある$e$について$5^e\mid F_{5^e}$が成立していることを仮定に置いて,
$5^{e+1}\mid F_{5^{e+1}}$即ち
$$
\begin{align}
5\mid\frac{F_{5^{e+1}}}{F_{5^e}}
\end{align}
$$を導くのであるが, より広く言って, 任意の整数$n$に対して
$$
\begin{align}
\frac{F_{5n}}{F_n}&=\frac{\phi^{5n}-\bar\phi^{5n}}{\phi^n-\bar\phi^n}\\
&=L_{4n}+(-1)^nL_{2n}+1
\end{align}
$$は$5$の倍数である. と言うのも, 数列$(L_n)$の${\rm mod}\ 5$による還元は
$$
\begin{align}
\ldots,2,1,3,4,2,1,3,4,\ldots
\end{align}
$$のような$4$項毎の周期列であり, $n$の偶奇で場合を分けてそれぞれ計算すると剰余が零に等しくなることが判るからである.
由って, 命題は再帰的に証明された. $\quad\Box$
$n$が$12$の倍数であるような場合について考察の余地は残るが, ここでは充分性を持つような$n$の無数性を証明するに留めておく.
$12$の正倍数$n$であって, $F_n$が$n$の倍数であるようなものは無数に存在する.
これは最大公約数の定理から導かれることであるが, 任意の正整数$m,n$について
$$
\begin{align}
m\mid n\Longrightarrow F_m\mid F_n
\end{align}
$$が成りたつ. 数列$(a_n)_{n>0}$を初期値と漸化式
$$
\begin{align}
a_1=12,\ a_{n+1}=F_{a_n}
\end{align}
$$によって定義すると, その全ての項は$12$の倍数であり, かつ関係式$a_n\mid F_{a_n}$を充たすことが再帰的に確かめられる. $(a_n)$は無限列であるため, 命題は証明された. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$5$や$12$といった数は, Lucas 数や Fibonacci 数に関する数論的な問題を考えてみるとよく出会う番号ではあります. これはこれで (数理的には当然ながらも) 不思議なことですが, とは言え, $5$と$12$の二つが一つの問題の解としてこのように表れてくれると, この問題のような黄金数列での整除性に, 更に妙々なる希少さを感じてしまうものです...
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
