黄金の加法定理

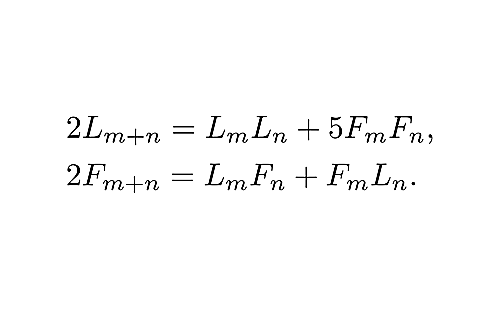加法定理の一
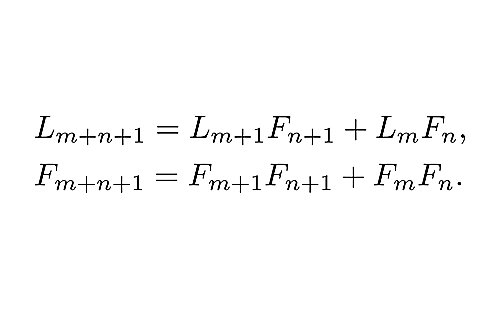加法定理の二
前提知識 : 数学的帰納法, Lucas 数列, Fibonacci 数列, 三角関数の加法定理, (有理) 整数環のイデアル
Fibonacci 数列 : https://mathlog.info/articles/191
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
修正版 : 黄金数の加法定理 ( https://mathlog.info/articles/2184 )
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

三角関数との類似性

加法定理の四つの等式は, その式形から再帰法を用いれば容易に証明することができるのであるが, 先ずはこれらのみかたを述べる.

第一種の加法定理
$$ \begin{align} &2L_{m+n}=L_mL_n+5F_mF_n\\ &2F_{m+n}=L_mF_m+F_mL_n \end{align}$$について, これらの等式は三角関数の加法定理
$$ \begin{align} &\cos{(x+y)}=\cos{x}\cos{y}-\sin{x}\sin{y}\\ &\sin{(x+y)}=\cos{x}\sin{y}+\sin{x}\cos{y} \end{align} $$と構造を同じくしていることが見て取れるであろう. この性質は, 黄金比の累乗を表す等式
$$ \begin{align} &2\phi^n=L_n+\sqrt{5}F_n\\ &2\bar{\phi}^n=L_n-\sqrt{5}F_n \end{align} $$が, Euler の公式
$$ \begin{align} &e^{ix}=\cos{x}+i\sin{x}\\ &e^{-ix}=\cos{x}-i\sin{x} \end{align} $$に似かようことに着眼すれば, 説明を付けることが可能である. ただし, $i$は虚数単位と見る.

ここで, 複素数の全体における三角関数の加法定理が, 複素三角関数の定義式, すなわち Euler の公式の単純な拡張から
$$ \begin{align} &e^{i(x+y)}=e^{ix}e^{iy}\\ \Longleftrightarrow&\;\cos{(x+y)}+i\sin{(x+y)}=(\cos{x}+i\sin{x})(\cos{y}+i\sin{y})\\ \Longleftrightarrow&\;\cos{(x+y)}+i\sin{(x+y)}\\ &\;\qquad=(\cos{x}\cos{y}-\sin{x}\sin{y})+i(\cos{x}\sin{y}+\sin{x}\cos{y})\\ \Longleftrightarrow&\;\begin{cases} \cos{(x+y)}=\cos{x}\cos{y}-\sin{x}\sin{y}\\ \sin{(x+y)}=\cos{x}\sin{y}+\sin{x}\cos{y} \end{cases} \end{align} $$と導出されることを確認しておく.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

組みあわせ論的なみかた

第二種の加法定理
$$ \begin{align} &L_{m+n+1}=L_{m+1}F_{n+1}+L_mF_n\\ &F_{m+n+1}=F_{m+1}F_{n+1}+F_mF_n \end{align} $$の第二式は Fibonacci 数のみによって記述される等式であり, $m,n$がともに正なるとき, 組みあわせ論的に解釈することが可能である. より詳しくは, $m+n$段の階段を一段上がりと二段上がりを用いて上る方法を考えるとき, その個数を二通りの手法によって総べれば得られる. 具体的な論証については, 次の記事を参照されたく思う.
Fibonacci 数の組みあわせ論的な性質とその応用 : https://mathlog.info/articles/210
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

整数論的なみかた

整数論的な立場では, たとえば, 第二種の加法定理の第二式にて$m$を$1$だけずらした等式
$$ \begin{align} F_{m+n}=F_{m}F_{n+1}+F_{m-1}F_{n} \end{align} $$および$$ \begin{align} F_{m-n}&=F_{m}F_{-n+1}+F_{m-1}F_{-n}\\ &=F_{m}F_{-n+1}+(-1)^{n+1}F_{m-1}F_{n} \end{align} $$は大いに顕著なる性質を映しだす. それは, 若し$(F_m,F_n)$の正なる公約数$d$を取れば, 上によって$F_{m+n},F_{m-n}$は何れも$F_m,F_n$の整数係数の線型結合に表されるため, これらにも$d$による整除性が移るということである. 従うに, 任意の正の整数$d$に対して, Fibonacci 数列の中で$d$の倍数であるような項のインデックスの成す集合*****
$$ \begin{align} I_F(d)=\{i\in\mathbb{Z}\mid F_i\in d\mathbb{Z}\} \end{align} $$は (有理) 整数環$\mathbb{Z}$のイデアルと成り, Fibonacci 数列中の$d$の倍数は$\mathbb{Z}$において均等に並ぶことが判る.
$\color{white}.\color{black}$
※これは, 任意の$d$に対して空でないことが知られている.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

帰納的証明

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$