Fibonacci 数を含む基礎的な無限級数 (2) 有名な無限和
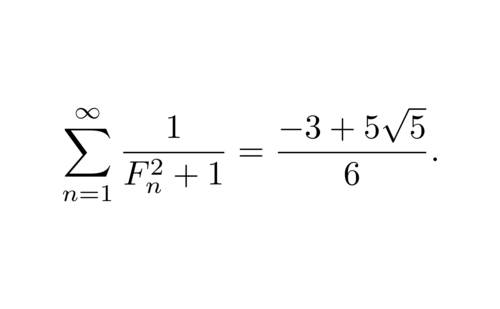 F_n^2 + 1 の逆数和
F_n^2 + 1 の逆数和
前提知識 : Lucas 数列, Fibonacci 数列
Lucas 数列, Fibonacci 数列 :
https://mathlog.info/articles/191
(1) の記事 :
https://mathlog.info/articles/1468
(3) の記事 : (準備中)
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
最新版 :
https://yu200489144.hatenablog.com/entry/2021/01/05/232023
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
Fibonacci 数の積の逆数和
$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_n}=1$が成りたつ.
$F_{n+1}=F_{n+2}-F_n$であることを用いれば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_n}&=\sum_{n\geqslant1}^n\frac{F_{n+2}-F_n}{F_{n+2}F_{n+1}F_n}\\
&=\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+1}F_n}-\frac{1}{F_{n+2}F_{n+1}}\right)\\
&=\frac{1}{F_1F_2}=1
\end{align}
$$と計算できる. $\quad\Box$
$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{n+3}F_{n+2}F_n}=1$が成りたつ.
$2F_{n+1}=F_{n+1}+F_{n+2}-F_n=F_{n+3}-F_n$であることを用いれば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{n+3}F_{n+2}F_n}&=\sum_{n\geqslant1}^n\frac{F_{n+3}-F_n}{2F_{n+3}F_{n+2}F_{n+1}F_n}\\
&=\frac{1}{2}\sum_{n\geqslant1}^n\left(\frac{1}{F_{n+2}F_{n+1}F_n}-\frac{1}{F_{n+3}F_{n+2}F_{n+1}}\right)\\
&=\frac{1}{2}\frac{1}{F_1F_2F_3}=\frac{1}{4}
\end{align}
$$と計算できる. $\quad\Box$
$\displaystyle\sum_{n\geqslant1}^n\frac{F_{n+1}}{F_{n+2}F_n}=2$が成りたつ.
(省略).
$\displaystyle\sum_{n\geqslant1}^n\frac{F_{n+1}}{F_{n+3}F_n}=\frac{5}{4}$が成りたつ.
(省略).
$\displaystyle\sum_{n\geqslant1}^n\frac{F_{4n+3}}{F_{2n+3}F_{2n+2}F_{2n+1}F_{2n}}=1$が成りたつ.
加法定理から
$$
\begin{align}
F_{4n+3}&=F_{4n+4}-F_{4n+2}\\
&=F_{(2n+2)+(2n+1)+1}-F_{(2n+1)+2n+1}\\
&=F_{2n+3}F_{2n+2}+F_{2n+2}F_{2n+1}-F_{2n+2}F_{2n+1}-F_{2n+1}F_{2n}\\
&=F_{2n+3}F_{2n+2}-F_{2n+1}F_{2n}
\end{align}
$$であることを用いれば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{F_{4n+3}}{F_{2n+3}F_{2n+2}F_{2n+1}F_{2n}}&=\sum_{n\geqslant1}^n\left(\frac{1}{F_{2n+1}F_{2n}}-\frac{1}{F_{2n+3}F_{2n+2}}\right)\\
&=\frac{1}{F_2F_1}=1
\end{align}
$$と計算できる. $\quad\Box$
続いて, 分子に$(-1)^n$が掛けられているような無限級数を扱う.
$\displaystyle\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+1}F_n}=\bar{\phi}$が成りたつ.
加法定理および符号の反転公式から
$$
\begin{align}
(-1)^n&=(-1)^n\frac{F_{(n+1-1)-n+1}}{F_1}\\
&=\frac{(-1)^n(F_{n+1}F_{-n+1}+F_{n+1-1}F_{-n})}{F_1}\\
&=F_{n+1}F_{n-1}-F_{n}F_{n}
\end{align}
$$であるので,
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+1}F_n}&=\sum_{n\geqslant1}^n\frac{F_{n+1}F_{n-1}-F_{n}F_{n}}{F_{n+1}F_n}\\
&=\sum_{n\geqslant1}^n\left(\frac{F_{n-1}}{F_n}-\frac{F_{n}}{F_{n+1}}\right)\\
&=\lim_{\ell\to\infty}\sum_{n=1}^{n=\ell}\left(\frac{F_{n-1}}{F_n}-\frac{F_{n}}{F_{n+1}}\right)\\
&=\lim_{\ell\to\infty}\left(\frac{F_0}{F_1}-\frac{F_{\ell}}{F_{\ell+1}}\right)\\
&=\lim_{\ell\to\infty}\left(-\frac{F_\ell}{F_\ell+1}\right)=-\frac{1}{\phi}
\end{align}
$$と纏められ, 最後に$\phi\bar\phi=-1$であることを適用すれば命題の式を得ることができる. $\quad\Box$
この結果の一つの拡張として, 次の定理を紹介する.
任意の正の整数$k$に対して,
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+k}F_n}=\frac{1}{F_k}\left(k\bar{\phi}+\sum_{n=1}^{n+1=k}\frac{F_n}{F_{n+1}}\right)
\end{align}
$$が成りたつ.
加法定理および符号の反転公式から
$$
\begin{align}
(-1)^n&=(-1)^n\frac{F_{(n+k-1)+(-n)+1}}{F_k}\\
&=\frac{(-1)^n(F_{n+k}F_{-n+1}+F_{n+k-1}F_{-n})}{F_k}\\
&=\frac{F_{n+k}F_{n-1}-F_{n+k-1}F_{n}}{F_k}
\end{align}
$$であるので,
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+k}F_n}&=\frac{1}{F_k}\sum_{n\geqslant1}^n\frac{F_{n+k}F_{n-1}-F_{n+k-1}F_{n}}{F_{n+k}F_n}\\
&=\frac{1}{F_k}\sum_{n\geqslant1}^n\left(\frac{F_{n-1}}{F_n}-\frac{F_{n+k-1}}{F_{n+k}}\right)\\
&=\frac{1}{F_k}\lim_{\ell\to\infty}\sum_{n=1}^{n=\ell}\left(\frac{F_{n-1}}{F_n}-\frac{F_{n+k-1}}{F_{n+k}}\right)\\
&=\frac{1}{F_k}\lim_{\ell\to\infty}\left(\sum_{n=1}^{n=k}\frac{F_{n-1}}{F_{n}}-\sum_{n=\ell+1}^{n=\ell+k}\frac{F_{n-1}}{F_n}\right)\\
&=\frac{1}{F_k}\sum_{n=1}^{n=k}\frac{F_{n-1}}{F_{n}}-\lim_{\ell\to\infty}\sum_{n=1}^{n=k}\frac{F_{n+\ell-1}}{F_{n+\ell}}\\
&=\frac{1}{F_k}\left(-k\frac{1}{\phi}+\sum_{n=1}^{n=k}\frac{F_{n-1}}{F_{n}}\right)
\end{align}
$$と纏められ, 最後に$\phi\bar\phi=-1$であることを適用すれば命題の式を得ることができる. $\quad\Box$
$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{2n+1}F_{2n-1}}=-\bar{\phi}$かつ$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{2n+2}F_{2n}}=\bar\phi^2$が成りたつ.
上記二つの無限級数の収束値をそれぞれ$S,T$と置くと
$$
\begin{align}
S+T&=\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_{n}}=1,\\
T-S&=\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+2}F_{n}}=\frac{1}{F_2}\left(2\bar{\phi}+\frac{F_1}{F_2}\right)\\
&=2\bar{\phi}^1+\bar{\phi}^0=\bar\phi^2+\bar{\phi}^1=\bar{\phi}^3
\end{align}
$$が先の定理により成りたつから, これらを$(S,T)$について変形して,
$$
\begin{align}
S&=\frac{1-\bar\phi^3}{2}=\frac{1-\bar\phi-\bar\phi^2}{2}=\frac{-2\bar\phi-(\bar\phi^2-\bar\phi-1)}{2}=-\bar{\phi},\\
T&=\frac{1+\bar{\phi}^3}{2}=\frac{\bar{\phi}^2-\bar{\phi}+\bar{\phi}^2+\bar{\phi}}{2}=\bar{\phi}^2
\end{align}
$$とそれぞれの値を得ることができる. $\quad\Box$
$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{n+1}F_n}=S_1$と置けば, $\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{2n}F_{2n-1}}=\frac{S_1-\bar\phi}{2}$かつ$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{2n+1}F_{2n}}=\frac{S_1+\bar\phi}{2}$が成りたつ.
(省略).
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
Fibonacci 数の多項式形の逆数和
$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}+1}=\phi$かつ$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}-1}=\phi^2$が成りたつ.
二つの無限級数をそれぞれ$S,T$と置く. Cassini の公式により$F_{2n-1}^2-1=F_{2n}F_{2n-2}$が成立することを用いると
$$
\begin{align}
S+T&=\sum_{n\geqslant2}^n\frac{2F_{2n-1}}{F_{2n-1}^2-1}=2\sum_{n\geqslant2}\frac{F_{2n}-F_{2n-2}}{F_{2n}F_{2n-2}}\\
&=2\sum_{n\geqslant2}\left(\frac{1}{F_{2n-2}}-\frac{1}{F_{2n}}\right)=2,\\
T-S&=\sum_{n\geqslant2}^n\frac{2}{F_{2n-1}^2-1}=2\sum_{n\geqslant2}\frac{1}{F_{2n}F_{2n-2}}\\
&=2\cdot\frac{1}{2}\left(\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_n}+\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+2}F_n}\right)\\
&=1+\frac{1}{F_2}\left(2\bar{\phi}+\frac{F_1}{F_2}\right)=2+2\bar\phi
\end{align}
$$が成りたつから, これらを$(S,T)$について変形して,
$$
\begin{align}
S&=\frac{2-(2+2\bar\phi)}{2}=-\bar{\phi},\\
T&=\frac{2+(2+2\bar{\phi})}{2}=1+(1+\bar{\phi})=1+\bar{\phi}^2=-({\phi}-\bar\phi)\bar{\phi}=-\sqrt{5}\bar{\phi}
\end{align}
$$とそれぞれの値を得ることができる. 但し, 途中で$\phi\bar{\phi}=-1$であることを適用した. $\quad\Box$
$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2+1}=-\bar\phi-\frac{1}{2}$かつ$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2-1}=\bar\phi^2$が成りたつ.
Cassini の公式により$F_{2n}^2+1=F_{2n+1}F_{2n-1}$かつ$F_{2n-1}^2-1=F_{2n}F_{2n-2}$が成立することを用いると
$$
\begin{align}
\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2+1}&=\sum_{n\geqslant2}\frac{1}{F_{2n+1}F_{2n-1}}\\
&=\frac{1}{2}\left(\sum_{n\geqslant2}^n\frac{1}{F_{n+2}F_n}-\sum_{n\geqslant2}^n\frac{(-1)^n}{F_{n+2}F_n}\right)\\
&=\frac{1}{2}\left(\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_n}-\frac{1}{2}-\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+2}F_n}-\frac{1}{2}\right)\\
&=\frac{1}{2}\left(1-\frac{1}{2}-\frac{1}{F_2}\left(2\bar{\phi}+\frac{F_1}{F_2}\right)-\frac{1}{2}\right)\\
&=-\bar\phi-\frac{1}{2},\\
\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2-1}&=\sum_{n\geqslant2}\frac{1}{F_{2n}F_{2n-2}}\\
&=\frac{1}{2}\left(\sum_{n\geqslant1}^n\frac{1}{F_{n+2}F_n}+\sum_{n\geqslant1}^n\frac{(-1)^n}{F_{n+2}F_n}\right)\\
&=\frac{1}{2}\left(1+\frac{1}{F_2}\left(2\bar{\phi}+\frac{F_1}{F_2}\right)\right)\\
&=1+\bar\phi=\bar\phi^2
\end{align}
$$と計算できる.
$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2-1}=\frac{8-3\sqrt{5}}{9}$かつ$\displaystyle\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2+1}=\frac{-3+2\sqrt{5}}{6}$が成りたつ.
Catalan の公式により$F_{2n}^2-1=F_{2n+2}F_{2n-2}$かつ$F_{2n-1}^2+1=F_{2n+1}F_{2n-3}$が成立することを用いると
$$
\begin{align}
\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2-1}&=\sum_{n\geqslant2}\frac{1}{F_{2n+2}F_{2n-2}}=\frac{1}{3}\sum_{n\geqslant2}\frac{3F_{2n}}{F_{2n+2}F_{2n}F_{2n-2}},\\
\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2+1}&=\sum_{n\geqslant2}\frac{1}{F_{2n+1}F_{2n-3}}=\frac{1}{3}\sum_{n\geqslant2}\frac{3F_{2n-1}}{F_{2n+1}F_{2n-1}F_{2n-3}}
\end{align}
$$のように変形でき, ここに漸化式$3F_{n}=F_{n+2}+F_{n-2}$を適用すれば
$$
\begin{align}
\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2-1}&=\frac{1}{3}\sum_{n\geqslant2}^n\frac{F_{2n+2}+F_{2n-2}}{F_{2n+2}F_{2n}F_{2n-2}},\\
&=\frac{1}{3}\left(\sum_{n\geqslant2}^n\frac{1}{F_{2n}F_{2n-2}}+\sum_{n\geqslant2}^n\frac{1}{F_{2n+2}F_{2n}}\right)\\
&=\frac{1}{3}\left(-\frac{1}{3}+2\sum_{n\geqslant2}^n\frac{1}{F_{2n}F_{2n-2}}\right),\\
\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2+1}&=\frac{1}{3}\sum_{n\geqslant2}^n\frac{F_{2n+3}+F_{2n-1}}{F_{2n+3}F_{2n+1}F_{2n-1}},\\
&=\frac{1}{3}\left(\sum_{n\geqslant2}^n\frac{1}{F_{2n+1}F_{2n-1}}+\sum_{n\geqslant2}^n\frac{1}{F_{2n+3}F_{2n+1}}\right)\\
&=\frac{1}{3}\left(-\frac{1}{2}+2\sum_{n\geqslant2}^n\frac{1}{F_{2n+1}F_{2n-1}}\right)
\end{align}
$$と纏められる. 一つ前の命題での議論を借りて計算すれば
$$
\begin{align}
\sum_{n\geqslant2}^n\frac{1}{F_{2n}^2-1}&=\frac{1}{3}\left(-\frac{1}{3}+2\bar\phi^2\right)=\frac{8-3\sqrt5}{9},\\
\sum_{n\geqslant2}^n\frac{1}{F_{2n-1}^2+1}&=\frac{1}{3}\left(-\frac{1}{2}-2\bar\phi\right)=\frac{-3+2\sqrt{5}}{6}
\end{align}
$$となる. $\quad\Box$
$\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^2+1}=\frac{-15+5\sqrt{5}}{6}$かつ$\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^2-1}=\frac{43-15\sqrt{5}}{43}$が成りたつ.
$n$を偶奇分けして足しあわせれば, 一つ前および二つ前の命題から計算することができる (省略).
$\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^4-1}=\frac{35-15\sqrt{5}}{18}$が成りたつ.
部分分数分解をすると
\begin{align}
\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^4-1}=\frac{1}{2}\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^2-1}-\frac{1}{2}\displaystyle\sum_{n\geqslant3}^n\frac{1}{F_n^2+1}
\end{align}
となること, および一つ前の命題から得られる (省略).
$\displaystyle\sum_{n\geqslant3}^n\frac{(-1)^n}{F_n^4-1}=-\frac{1}{18}$が成りたつ.
Catalan の等式から
$$
\begin{align}
F_n^4-1&=
\begin{cases}
(F_n^2+F_1^2)(F_n^2-F_2^2)\quad&(n:{\rm even})\\
(F_n^2+F_2^2)(F_n^2-F_1^2)\quad&(n:{\rm odd})
\end{cases}\\
&=
\begin{cases}
F_{n+1}F_{n-1}F_{n+2}F_{n-2}\quad&(n:{\rm even})\\
F_{n+2}F_{n-2}F_{n+1}F_{n-1}\quad&(n:{\rm odd})
\end{cases}\\
&=F_{n+2}F_{n+1}F_{n-1}F_{n-2},\\
(-1)^n&=(-1)^n\frac{F_{(n+1)+(-n+1)+1}}{F_3}\\
&=(-1)^n\frac{F_{n+2}F_{-n+2}+F_{n+1}F_{-n+1}}{2}\\
&=\frac{-F_{n+2}F_{n-2}+F_{n+1}F_{n-1}}{2}
\end{align}
$$であるため,
$$
\begin{align}
\sum_{n\geqslant3}^n\frac{(-1)^n}{F_n^4-1}&=\frac{1}{2}\sum_{n\geqslant3}^n\frac{F_{n+1}F_{n-1}-F_{n+2}F_{n-2}}{F_{n+2}F_{n+1}F_{n-1}F_{n-2}}\\
&=\frac{1}{2}\sum_{n\geqslant3}^n\left(\frac{1}{F_{n+2}F_{n-2}}-\frac{1}{F_{n+1}F_{n-1}}\right)
\end{align}
$$と分離することができる. 漸化式$3F_n=F_{n+2}+F_{n-2}$を用いてそれぞれの和を計算すれば
$$
\begin{align}
\sum_{n\geqslant3}^n\frac{1}{F_{n+2}F_{n-2}}&=\sum_{n\geqslant3}^n\frac{F_{n+2}+F_{n-2}}{3F_{n+2}F_nF_{n-2}}\\
&=\frac{1}{3}\sum_{n\geqslant3}^n\left(\frac{1}{F_nF_{n-2}}+\frac{1}{F_{n+2}F_n}\right)\\
&=\frac{1}{3}\left(1+1-\frac{1}{2}-\frac{1}{3}\right)=\frac{7}{18},\\
\sum_{n\geqslant3}^n\frac{1}{F_{n+1}F_{n-1}}&=1-\frac{1}{2}=\frac{1}{2}
\end{align}
$$と$\sum_{n\geqslant1}^n1/F_{n+2}F_n=1$から導かれ, 元の級数の収束値は
$$
\begin{align}
\sum_{n\geqslant3}^n\frac{(-1)^n}{F_n^4-1}&=\frac{1}{2}\sum_{n\geqslant3}^n\left(\frac{1}{F_{n+2}F_{n-2}}-\frac{1}{F_{n+1}F_{n-1}}\right)\\
&=\frac{1}{2}\left(\frac{7}{18}-\frac{1}{2}\right)=-\frac{1}{18}
\end{align}
$$であることが判る. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
Millin の級数
次に, $1/F_{2^n}$の無限和の幾通りかの計算手法を示す. 因みに, 級数の名称の由来となった D. A. Miller の本名は Millin ではなく Miller である.
$\displaystyle\sum_{n\geqslant1}^n\frac{1}{F_{2^n}}=-\sqrt{5}\bar\phi$が成りたつ.
収束範囲で
$$
\begin{align}
F(x)=\sum_{n\geqslant1}^n\frac{x^{2^{n-1}}}{F_{2^n}}
\end{align}
$$なる級数を考える. 数列$(L_n)$および$(F_n)$の一般項から
$$
\begin{align}
F(\phi x)+F(\bar\phi x)&=\sum_{n\geqslant1}^n\frac{\phi^{2^{n-1}}+\bar\phi^{2^{n-1}}}{F_{2^n}}x^{2^{n-1}}\\
&=\sum_{n\geqslant1}^n\frac{x^{2^{n-1}}}{F_{2^{n-1}}}\\
&=x+F(x^2)
\end{align}
$$が成立するので, $x=-\bar\phi$を代入して
$$
\begin{align}
F(1)+F(-\bar\phi^2)=-\bar\phi+F(\bar\phi^2)
\end{align}
$$即ち
$$
\begin{align}
F(1)&=-\bar\phi+F(\bar\phi^2)-F(-\bar\phi^2)\\
&=-\bar\phi+\sum_{n\geqslant1}^n\frac{(\bar\phi^2)^{2^{n-1}}}{F_{2^n}}-\sum_{n\geqslant1}^n\frac{(-\bar\phi^2)^{2^{n-1}}}{F_{2^n}}\\
&=-\bar\phi+\sum_{n=1}^{n=1}\left(\frac{(\bar\phi^2)^{2^{n-1}}}{F_{2^n}}-\frac{(-\bar\phi^2)^{2^{n-1}}}{F_{2^n}}\right)\\
&=-\bar\phi+2\bar\phi^2=1+\bar\phi^2\\
&=(\bar\phi-\phi)\bar\phi=-\sqrt{5}\bar\phi
\end{align}
$$を得る. $\quad\Box$
一般項を直接代入して進めると
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{2^n}}&=\sum_{n\geqslant1}^n\frac{\phi-\bar\phi}{\phi^{2^n}-\bar{\phi}^{2^n}}=\sum_{n\geqslant1}^n\frac{\phi-\bar{\phi}}{\phi^{2^n}-\phi^{-2^n}}\\
&=\sum_{n\geqslant1}^n\frac{\phi-\bar\phi}{\phi^{2^{n}}}\frac{1}{1-\phi^{-2^{n+1}}}\\
&=\sum_{n\geqslant1}^n\frac{\phi-\bar\phi}{\phi^{2^{n}}}\sum_{m\geqslant0}^m\phi^{-2^{n+1}m}\\
&=\sum_{n\geqslant1}^n\sum_{m\geqslant0}^m\frac{\phi-\bar\phi}{\phi^{2^{n}(2m+1)}}\\
&=\sum_{\ell\geqslant1}^\ell\frac{\phi-\bar\phi}{\phi^{2\ell}}\\
&=\frac{(\phi-\bar\phi)\phi^{-2}}{1-\phi^{-2}}=\frac{\phi-\bar\phi}{\phi^2-1}\\
&=\frac{\phi-\bar\phi}{\phi}=-\sqrt{5}\bar\phi
\end{align}
$$のように計算することができる. 但し, 途中で$\phi\bar\phi=-1$であることを適用した. $\quad\Box$
Millin の級数の部分和が, あらゆる正の整数$\ell$に対して
$$
\begin{align}
\sum_{n=1}^{n=\ell}\frac{1}{F_{2^n}}=3-\frac{F_{2^\ell+1}}{F_{2^\ell}}
\end{align}
$$のように簡約されることを証明する. ある$\ell$においてこのようであるのなら, 次の$\ell+1$においても
$$
\begin{align}
\sum_{n=1}^{n=\ell+1}\frac{1}{F_{2^n}}&=3-\frac{F_{2^\ell+1}}{F_{2^\ell}}+\frac{1}{F_{2^{\ell+1}}}\\
&=3-\frac{F_{2^\ell+1}F_{2^{\ell+1}}-F_{2^\ell}}{F_{2^\ell}F_{2^{\ell+1}}}\\
&=3-\frac{F_{e+1}F_{e+(e-1)+1}-F_{e}}{F_{e}F_{2e}}\qquad(2^\ell=e)\\
&=3-\frac{F_{e+1}(F_{e+1}F_e+F_eF_{e-1})-F_e}{F_eF_{2e}}\\
&=3-\frac{F_{e+1}^2+F_{e+1}F_{e-1}-1}{F_{2e}}\\
&=3-\frac{F_{e+1}^2+F_e^2}{F_{2e}}\\
&=3-\frac{F_{e+e+1}}{F_{2e}}=3-\frac{F_{2^{\ell+1}+1}}{F_{2^{\ell+1}}}
\end{align}
$$のようになる. $\ell=1$のときに等号は成りたっているから, 由って全ての$\ell$に対して部分和は上記のように書くことができ, $\ell\to\infty$の極限を取れば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{2^n}}&=3-\phi=2+\bar\phi\\
&=\cdots=-\sqrt{5}\bar\phi
\end{align}
$$と元の無限級数の収束値が判る. 但し, 途中で$\phi+\bar\phi=1$であること, および一つ前の命題での議論の結果を用いた. $\quad\Box$
$2$以上なる整数$n$に対して
$$
\begin{align}
a_n=\frac{1}{(1+\phi^4)(1+\phi^8)\cdots(1+\phi^{2^n})}
\end{align}
$$なる実数$a_n$を定義すると, $(a_n)$の階差は
$$
\begin{align}
a_{n+1}-a_n&=\frac{1}{(1+\phi^4)(1+\phi^8)\cdots(1+\phi^{2^n})(1+\phi^{2^{n+1}})}\\
&\qquad-\frac{1}{(1+\phi^4)(1+\phi^8)\cdots(1+\phi^{2^n})}\\
&=\frac{-\phi^{2^{n+1}}}{(1+\phi^4)(1+\phi^8)\cdots(1+\phi^{2^{n+1}})}\\
&=\frac{-\phi^{2^{n+1}}}{(\phi^{-2}+\phi^2)(\phi^{-4}+\phi^4)\cdots(\phi^{-2^n}+\phi^{2^n})\phi^{2+4+\cdots+2^n}}\\
&=\frac{-\phi^2}{(\phi^{-2}+\phi^2)(\phi^{-4}+\phi^4)\cdots(\phi^{-2^n}+\phi^{2^n})}\\
&=\frac{-(\phi^2-\bar\phi^2)\phi^2}{(\phi^2-\bar{\phi^2})(\phi^{-2}+\phi^2)(\phi^{-4}+\phi^4)\cdots(\phi^{-2^n}+\phi^{2^n})}\\
&=\frac{-(\phi^2-\bar\phi^2)\phi^2}{\phi^{2^{n+1}}-\phi^{-2^{n+1}}}=-\frac{\phi^2}{F_{2^{n+1}}}
\end{align}
$$のように整理されるため, 対象の級数は
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{1}{F_{2^n}}&=\frac{1}{F_2}+\frac{1}{F_4}+\sum_{n\geqslant2}^n\frac{1}{F_{2^{n+1}}}\\
&=\frac{4}{3}-\frac{1}{\phi^2}\sum_{n\geqslant2}^n(a_{n+1}-a_n)\\
&=\frac{4}{3}-\frac{1}{\phi^2}\lim_{n\to\infty}(a_{n+1}-a_2)\\
&=\frac{4}{3}-\frac{1}{\phi^2}\left(0-\frac{1}{1+\phi^4}\right)\\
&=\cdots=-\sqrt{5}\bar{\phi}
\end{align}
$$に収束する. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
参考文献 (リンク付き)
1( https://www.fq.math.ca/Scanned/7-2/brousseau1.pdf ) Brother Alfred Brousseau, "Summation of Infinite Fibonacci Series," The Fibonacci Quarterly, Vol.7 (1969), No.2; pp.143-168.
2( https://www.fq.math.ca/Scanned/7-2/brousseau3.pdf ) Brother Alfred Brousseau, "Fibonacci-Lucas Infinite Series Research Topic," The Fibonacci Quarterly, Vol.7 (1969), No.2; pp.211-217.
3( https://www.fq.math.ca/Problems/February2018AdvancedProblemREV.pdf ) Hideyuki Ohtsuka, "Advanced Problems and Solutions," H-783, The Fibonacci Quarterly, Vol.56 (2018), No.1; pp.90-91.
4( https://www.fq.math.ca/Scanned/14-2/advanced14-2.pdf ) D. A. Miller, "Advanced Problems and Solutions," H-237, The Fibonacci Quarterly, Vol.14 (1976), No.2; pp.186-187.
5( http://arxiv.org/abs/1603.03765v1 ) Chance Sanford, "Infinite Series Involving Fibonacci Numbers Via Apery-Like Formulae," (2016), CoRR; pp.1-15.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
