Fibonacci 数を含む基礎的な無限級数 (1) 母関数と一般項
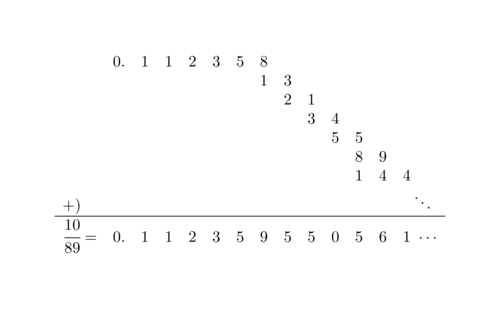 10/89
10/89
前提知識 : Lucas 数列, Fibonacci 数列
Lucas 数列, Fibonacci 数列 :
https://mathlog.info/articles/191
(2) の記事 :
https://mathlog.info/articles/1469
(3) の記事 : (準備中)
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
最新版 :
https://yu200489144.hatenablog.com/entry/2021/01/05/232023
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
準備
整数列$(L_n)_{n\in\mathbb{Z}},(F_n)_{n\in\mathbb{Z}}$であって, 漸化式および$L_0,F_0,L_1,F_1$の値
$$
\begin{align}
\begin{cases}
L_{n+2}=L_{n+1}+L_n,\quad L_0=2,\ L_1=1\\\\
F_{n+2}=F_{n+1}+F_n,\quad F_0=0,\ F_1=1
\end{cases}
\end{align}
$$によって定められるものそれぞれ Lucas 数列, Fibonacci 数列と呼ぶ.
任意の整数$n$に対して, $\left(\begin{array}{l}L_{-n}=(-1)^nL_n\\F_{-n}=(-1)^{n+1}F_n\end{array}\right.$が成りたつ.
$n=0,1$のときは正しい. それぞれの等式について, ある$n+1,n$について等式が成りたつならば, それらを辺々足しわせることで$n+2$の場合が得られ. また辺々を引けば$n-1$の場合が得られるので, 再帰的に命題は示された. $\quad\Box$
二次方程式$x^2=x+1$の二つの解のうち正なるものを黄金比, 負なるものを共役黄金比と呼んで, それぞれ$\phi,\bar{\phi}$と表す.
これに従えば
$$
\begin{align}
&\phi=\frac{1+\sqrt{5}}{2},&&\bar{\phi}=\frac{1-\sqrt{5}}{2},\\
&\phi+\bar{\phi}=1,&&\phi\bar{\phi}=-1
\end{align}
$$が成りたつ.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
母関数
数列$(L_n)_{n\geqslant0}$および$(F_n)_{n\geqslant0}$の収束範囲における母関数を, それぞれ
$$
\begin{align}
&l(x)=\sum_{n\geqslant0}^nL_nx^n,\\
&f(x)=\sum_{n\geqslant0}^nF_nx^n
\end{align}
$$という記号で表し, 右辺の級数の収束する$x$の領域を$I_l,I_f$と置く.
$l(x)$および$f(x)$は$\bar\phi< x<-\bar\phi$の範囲で収束し, その収束値は
$$
\begin{align}
l(x)=\frac{2-x}{1-x-x^2},\quad f(x)=\frac{x}{1-x-x^2}
\end{align}
$$である.
$x\in I_f$ならば
$$
\begin{align}
(1-x-x^2)f(x)&=(1-x-x^2)\sum_{n\geqslant0}^nL_nx^n\\
&=\sum_{n\geqslant0}^nF_nx^n-\sum_{n\geqslant0}^nF_nx^{n+1}-\sum_{n\geqslant0}^nF_nx^{n+2}\\
&=0+x+\sum_{n\geqslant2}^nF_{n}x^{n}-0x-\sum_{n\geqslant2}^nF_{n-1}x^{n}-\sum_{n\geqslant2}^nF_{n-2}x^{n}\\
&=x+\sum_{n\geqslant2}^n(F_n-F_{n-1}-F_{n-2})x^n=x
\end{align}
$$から$f(x)=x/(1-x-x^2)$が判り, 同様にして$x\in I_l$ならば$l(x)=(2-x)/(1-x-x^2)$であることが得られる. これらを部分分数分解し, $\phi\bar{\phi}=-1$を適用すると
$$
\begin{align}
\frac{2-x}{1-x-x^2}&=\frac{\phi}{\phi+x}+\frac{\bar\phi}{\bar\phi+x},\\
\frac{x}{1-x-x^2}&=\frac{1}{\phi-\bar\phi}\left(\frac{\bar\phi}{\bar\phi+x}-\frac{\phi}{\phi+x}\right)\\
\end{align}
$$となるため, 収束条件は何れも$|x|<|\phi|$かつ$|x|<|\bar{\phi}|$である. $0<-\bar\phi<\phi$であったから, これは
$$
\begin{align}
I_l=I_f=(\bar{\phi},-\bar\phi)
\end{align}
$$と書くことができる. $\quad\Box$
この命題から
$$
\begin{align}
\frac{19}{89}&=0.213483\cdots\\
\frac{10}{89}&=0.011235\cdots,\\
\frac{199}{9899}&=0.02010304071118\cdots,\\
\frac{100}{9899}&=0.00010102030508\cdots
\end{align}
$$などが判る. 因みに,
$$
\begin{align}
\frac{1}{89}=&0.\overline{0112359550561797752808}\\
&\color{white}0.\color{black}\overline{9887640449438202247191}
\end{align}
$$であり, 循環節の前半部$112359550561797752808$に$1$を足した数は
$$
\begin{align}
112359550561797752809\times99=11123595505617977528091
\end{align}
$$を充たす.
任意の整数$n$に対して, $\left(\begin{array}{l}L_n=\phi^n+\bar{\phi}^n\\F_n=\dfrac{\phi^n-\bar{\phi}^n}{\phi-\bar\phi}\end{array}\right.$が成りたつ.
母関数の収束値の部分分数分解の式は, $\phi\bar{\phi}=-1$を用いて
$$
\begin{align}
l(x)&=\frac{\phi}{\phi+x}+\frac{\bar{\phi}}{\bar{\phi}+x}\\
&=\frac{1}{1-\bar{\phi}x}+\frac{1}{1-\phi x}\\
&=\sum_{n\geqslant0}^n(\bar{\phi}^n+\phi^n)x^n,\\
(\phi-\bar\phi)f(x)&=\frac{\bar\phi}{\bar\phi+x}-\frac{\phi}{\phi+x}\\
&=\frac{1}{1-{\phi}x}-\frac{1}{1-\bar\phi x}\\
&=\sum_{n\geqslant0}^n({\phi}^n-\bar\phi^n)x^n
\end{align}
$$と更に変形することができ, 両辺で$x^n$の係数を比較すれば$n\geqslant0$の場合の得られる. $n\leqslant0$のときは, 符号の反転公式から
$$
\begin{align}
L_n&=(-1)^nL_{-n}\\
&=(\phi\bar\phi)^n(\phi^{-n}+\bar\phi^{-n})\\
&=\phi^n+\bar\phi^n,\\
F_n&=(-1)^{n-1}F_{-n}\\
&=-(\phi\bar\phi)^n\frac{\phi^{-n}-\bar\phi^{-n}}{\phi-\bar\phi}\\
&=\frac{\phi^n-\bar\phi^n}{\phi-\bar\phi}
\end{align}
$$
のように拡張されるため, 全ての整数$n$について証明が完了した.$\quad\Box$
$\displaystyle\lim_{n\to\infty}\frac{L_{n+1}}{L_n}=\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\phi$が成りたつ.
$-1<\bar{\phi}<0$に注意すれば, 一般項を代入して
$$
\begin{align}
&\lim_{n\to\infty}\frac{L_{n+1}}{L_n}=\lim_{n\to\infty}\frac{\phi^{n+1}+\bar{\phi}^{n+1}}{\phi^n+\bar{\phi}^n}=\phi,\\
&\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\lim_{n\to\infty}\frac{\phi^{n+1}-\bar{\phi}^{n+1}}{\phi^n-\bar{\phi}^n}=\phi
\end{align}
$$と計算できる. $\quad\Box$
$\displaystyle\lim_{n\to\infty}\frac{L_n}{F_n}=\sqrt5$が成りたつ.
$-1<\bar{\phi}<0$に注意すれば, 一般項を代入して
$$
\begin{align}
\lim_{n\to\infty}\frac{L_n}{F_n}=\lim_{n\to\infty}\sqrt{5}\frac{\phi^{n}+\bar{\phi}^{n}}{\phi^n-\bar{\phi}^n}=\sqrt{5}
\end{align}
$$と計算できる. $\quad\Box$
任意の整数$m,n$に対して, 以下が成りたつ.
$\quad({\rm 1L})\quad2L_{m+n}=L_mL_n+5F_mF_n.$
$\quad({\rm 1F})\quad2F_{m+n}=L_mF_n+F_mL_n.$
$\quad({\rm 2L})\quad L_{m+n+1}=L_{m+1}F_{n+1}+L_mF_n.$
$\quad({\rm 2F})\quad F_{m+n+1}=F_{m+1}F_{n+1}+F_mF_n.$
後ろの二式は, 漸化式を繰りかえし用いて得られる等式類
$$
\begin{align}
L_{n+2}&=L_{n+1}+L_n,\\
L_{n+3}&=L_{n+2}+L_{n+1}=2L_{n+1}+L_n,\\
L_{n+4}&=L_{n+3}+L_{n+2}=2L_{n+2}+L_{n+2}=3L_{n+1}+2L_n,\\
&\;\;\vdots\\
F_{n+2}&=F_{n+1}+F_n,\\
F_{n+3}&=F_{n+2}+F_{n+1}=2F_{n+1}+F_n,\\
F_{n+4}&=F_{n+3}+F_{n+2}=2F_{n+2}+F_{n+2}=3F_{n+1}+2F_n,\\
&\;\;\vdots
\end{align}
$$の一般化であり, このような再帰性を用いて帰納的に等号の成立を確かめるほうが簡明であるが, ここでは一般項および母関数を用いた証明を記す.
$(1)\quad$一般項から$\phi^n=(L_n+F_n\sqrt{5})/2$が導出されることを確かめておく. 指数の等式$\phi^{m+n}=\phi^m\phi^n$にこれを代入して展開すると
$$
\begin{align}
&\phi^{m+n}=\phi^m\phi^n\\
\Longleftrightarrow\;&\frac{L_{m+n}+F_{m+n}\sqrt{5}}{2}=\frac{L_m+F_m\sqrt{5}}{2}\frac{L_n+F_n\sqrt{5}}{2}\\
\Longleftrightarrow\;&2L_{m+n}+2F_{m+n}\sqrt{5}=(L_mL_n+5F_mF_n)+(L_mF_n+F_mL_n)\sqrt{5}
\end{align}
$$と同値変形され, $\sqrt{5}$の無理数性から, 有理数部分と無理数部分を比較して加法定理を得る. $\quad\Box$
$(2)\quad$閉区間$(\bar\phi,-\bar\phi)$上で母関数$f$の収束値から等式$(2{\rm F})$を確かめる. 先ず左辺について,
$$
\begin{align}
\sum_{m,n\geqslant0}^{m,n}F_{m+n+1}x^{m+n}&=\frac{1}{x}\sum_{m,n\geqslant0}^{m,n}F_{m+n+1}x^{m+n+1}\\
&=\frac{1}{x}\sum_{\ell\geqslant1}^\ell\ell F_\ell x^\ell\\
&=\frac{{\rm d}(f-F_0x^0)}{{\rm d}x}=\frac{{\rm d}f}{{\rm d}x}\\
&=\frac{1(1-x-x^2)-x(-1-2x)}{(1-xs-x^2)^2}\\
&=\frac{1+x^2}{(1-x-x^2)^2}
\end{align}
$$と分数式として表しなおすことができる. また右辺については
$$
\begin{align}
&\sum_{m,n\geqslant0}^{m,n}(F_{m+1}F_{m+1}+F_mF_n)x^{m+n}\\
=\;&\left(\frac{f-F_0x^0}{x}\right)^2+f^2\\
=\;&\frac{1}{(1-x-x^2)^2}+\frac{x^2}{(1-x-x^2)^2}\\
=\;&\frac{1+x^2}{(1-x-x^2)^2}
\end{align}
$$
となり, 上記二つは相等しいので等式は正しい. 等式$(2{\rm L})$についても同様であるので, その詳細は省略する. 最後に, 両辺に$(-1)^{m+n+1},(-1)^{m+n}$をそれぞれ乗じれば非負なる整数に対する加法定理が導かれる. $\quad\Box$
参考 : https://mathlog.info/articles/320
任意の整数$n$に対して, $F_{n+1}F_{n-1}-F_n^2=(-1)^n$が成りたつ.
符号の反転公式と加法定理から,
$$
\begin{align}
(-1)^n&=(-1)^n\frac{F_{(n+1)-n+1}}{F_2}\\
&=(-1)^n\frac{F_{n+2}F_{-n+1}+F_{n+1}F_{-n}}{F_2}\\
&=F_{n+2}F_{n-1}-F_{n+1}F_n
\end{align}
$$と変形でき, ここに$F_{n+2}=F_{n+1}+F_n$を代入すれば
$$
\begin{align}
(-1)^n&=F_{n+1}F_{n-1}+F_nF_{n-1}-F_{n+1}F_n\\
&=F_{n+1}F_{n-1}+F_n(F_{n-1}-F_{n+1})\\
&=F_{n+1}F_{n-1}-F_n^2
\end{align}
$$と命題の式に達する. $\quad\Box$
参考 : https://mathlog.info/articles/223
この手法を一般化して, 等式
$$
\begin{align}
F_{n+k}F_{n-k}-F_n^2=(-1)^{n-k+1}F_k^2
\end{align}
$$あるいは
$$
\begin{align}
(-1)^n=\frac{F_{n+k}^2-F_{n+2k}F_n}{F_k^2}
\end{align}
$$があらゆる整数$k,n$について成立することを証明することができ, Catalan の等式と呼ばれるこれらの式が, $(-1)^n$の形を含む無限級数の収束値の計算において大いに役立つということを後の記事にて見る.
任意の整数$k,n$に対して, $F_{n+k}F_{n-k}-F_n^2=(-1)^{n-k+1}F_k^2$が成りたつ.
Catalan の等式と同様にして証明することができる (省略).
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
おまけ
任意の正の整数$n$に対して, $F_{n+1}=\displaystyle\sum_{m=0}^{m=n}\binom{n-m}{m}$が成りたつ.
$x\in I_f$の区間において
$$
\begin{align}
f(x)&=\frac{x}{1-x(1+x)}\\
&=x\sum_{n\geqslant0}^nx^n(1+x)^n\\
&=x\sum_{n\geqslant0}^nx^n\sum_{m=0}^{m=n}\binom{n}{m}x^m\\
&=x\sum_{n\geqslant0}^n\sum_{m=0}^{m=n}\binom{n}{m}x^{m+n}\\
&=x\sum_{N\geqslant m}^N\sum_{m=0}^{m=n}\binom{N-m}{m}x^{N}=x\sum_{N\geqslant0}^N\sum_{m=0}^{m=n}\binom{N-m}{m}x^{N}\\
&=\sum_{n\geqslant0}^n\left(\sum_{m=0}^{m=n}\binom{n-m}{m}\right)x^{n+1}
\end{align}
$$が成立し, $x^{n+1}$の項の係数から命題の式が得られる. $\quad\Box$
この命題は, 下のようなPascalの三角形において右上がりの斜め和がFibonacci数列の項になることを主張しており, 実際に計算して確かめることができる.
$$
\begin{align}
\begin{array}{c|ccccccccccc}
&0&1&2&3&4&5&6&7&8&\cdots\\\hline
0&1&&&&&&&&&\\
1&1&1&&&&&&&&\\
2&1&2&1&&&&&&&\\
3&1&3&3&1&&&&&&\\
4&1&4&6&4&1&&&&&\\
5&1&5&10&10&5&1&&&&\\
6&1&6&15&20&15&6&1&&&\\
7&1&7&21&35&35&21&7&1&&\\
8&1&8&28&56&70&56&28&8&1&\\
\vdots&&&&&&&&&&\ddots
\end{array}
\end{align}
$$
$\bar\phi< x<-\bar\phi$ならば$\displaystyle\exp\left(\sum_{n\geqslant1}^n\frac{L_n}{n}x^n\right)=\sum_{n\geqslant0}^nF_{n+1}x^{n}$が成りたつ.
Lucas 数の母関数の収束値から$L_0x^0$を引くと
$$
\begin{align}
l(x)-L_0x^0=\frac{2-x}{1-x-x^2}-2=x\frac{2x+1}{1-x-x^2}=-x\frac{(1-x-x^2)'}{1-x-x^2}
\end{align}
$$
のようになり, 両辺を$x$で割って積分すれば
$$
\begin{align}
\int{\rm d}x\sum_{n\geqslant1}^nL_nx^{n-1}=-\ln(1-x-x^2)+C
\end{align}
$$すなわち
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{L_n}{n}x^{n}=\ln\frac{x}{x(1-x-x^2)}+C
\end{align}
$$が得られる. $x=0$の場合の成立から$C=0$が判り, $f(x)=x/(1-x-x^2)$であったことを用いれば
$$
\begin{align}
\sum_{n\geqslant1}^n\frac{L_n}{n}x^{n}=\ln\frac{f(x)}{x}
\end{align}
$$という等式に変形され, 両辺を$\exp$によって飛ばせば命題の式になる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
