A Combinatorial Interpretation of @apu_yokai's k-Lucas Number Identity

Introduction

The Fibonacci numbers admit a straight-forward generalisation by modifying the recurrence relation $F_{n+1} = F_{n-1} + F_{n}$
to $f_{n+1} = f_{n-k+1} + \cdots + f_{n}$, that is, we replace the sum of two previous terms by the sum of $k$ previous terms.
Another way to write this recursion is via matrix multiplication:

$$ \begin{pmatrix} f_{n-k+2} \\ \vdots \\ f_{n+1} \end{pmatrix} = \underset{M_k^T :=}{\underbrace{ \begin{pmatrix} 0 & 1 & & 0 \\ \vdots & \ddots & \ddots & \\ 0 & \cdots & 0 & 1 \\ 1 & \cdots & \cdots & 1 \\ \end{pmatrix} }} \begin{pmatrix} f_{n-k+1} \\ \vdots \\ f_{n} \end{pmatrix} $$

This matrix $M_{k}$ has characteristic polynomial $x^{k} - x^{k-1} - \cdots - 1$, and by Cayley-Hamilton we get the identity $ M^{k} = M^{k-1} + \cdots + M + I, $ which encodes the recurrence relation of the $f_{i}$.
Furthermore the polynomial has $k$ roots $a_{1}, ..., a_{k}$, which are the eigenvalues of $M_{k}$.

An important companion of the Fibonacci numbers are the Lucas numbers $L_{n}$, which can be seen as the trace of powers of $M_{2}$:
$$ L_{n} = \trace(M_{2}^{n}) $$
Accordingly we can define the $k$-Lucas numbers to be $ \ell_{n} := \trace(M_{k}^{n}) = a_1^n + ... + a_k^n $.

For small $n$ the $k$-Lucas numbers have a surprisingly simple form: $\ell_{n} = 2^{n}-1$ for $1 \leq n \leq k$.
This has been observed by @apu_yokai and proven in a collaborative effort on Twitter and Mathlog.
The proof is short and uses Newton's identities.
For this article I want to go in a different direction and ask: Why $2^{n} - 1$? I found a combinatorial answer which I will present two steps:

1. View the matrix $M_{k}$ as a directed graph
2. Build finite deterministic automata from this directed graph which together produce all non-zero binary numbers.

The Graph

The Matrix $M = M_k$ is defined by

$ M e_{1} = e_{2}, \quad \ldots, \quad M e_{k-1} = e_{k} $ and $ M e_{k} = e_{1} + \ldots + e_{k} $.

This matrix is an adjacency matrix for the directed graph on $k$ nodes $1,\ldots,5$ with edges
$ 1 \to 2, \quad \ldots, \quad k-1 \to k $ and $ k \to 1, \quad \ldots, \quad k \to k $.

Here is an example for $k=5$:
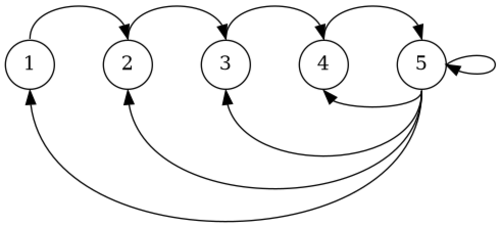Graph for k = 5

The powers of the adjacency matrix have a very useful interpretation, as explained in Wikipedia :
The $(i,j)$ entry in $M^{n}$ counts the number of paths of length $n$ to go from $j$ to $i$.

In particular, the trace counts the number of loops of length $n$ starting from any vertex.
(Caveat: two loops are considered different if their starting vertices are different, i.e. $1 \to 2 \to 3 \to 1 \neq 2 \to 3 \to 1 \to 2$)
The question now becomes: How many loops of length $n$ exist in this graph?

The Automaton

From the graph we obtain a machine which produces non-zero binary numbers by labeling the edges:

$$ \LABEL[i \to i+1] = 0, \quad (i = 1,...,k-1) $$
$$ \LABEL[k \to i] = 1, \quad (i = 1,...,k) $$

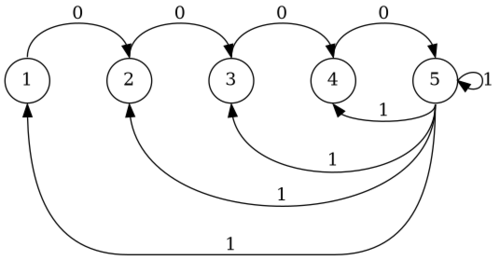Automaton for k = 5

To produce the binary number 00101 we use the loop $3 \overset{0}\to 4 \overset{0}\to 5 \overset{1}\to 4 \overset{0}\to 5 \overset{1}\to 3$

More examples:

00001: $1 \overset{0}\to 2 \overset{0}\to 3 \overset{0}\to 4 \overset{0}\to 5 \overset{1}\to 1$

1101: $5 \overset{1}\to 5 \overset{1}\to 4 \overset{0}\to 5 \overset{1}\to 5$

00100: $3 \overset{0}\to 4 \overset{0}\to 5 \overset{1}\to 1 \overset{0}\to 2 \overset{0}\to 3$

I think you can show by induction that every non-zero binary number of length $n$ is produced by a unique loop of length $n$ ($1 \leq n \leq k$).
The number of loops is therefore the number of non-zero binary numbers on $n$ bits, which is $2^n - 1$.