積分の続き
前回の記事(
https://mathlog.info/articles/1752
) では, Don@ld氏の問題,
$$\begin{eqnarray}
I=\int_{-\infty}^{\infty}\frac{e^{\pi/2}\left(2t\cos\left(e^{\pi t/2}+\frac{\pi}4\right)+(t^2+3)\sin\left(e^{\pi t/2}+\frac{\pi}4\right)\right)}{(t^2+1)(t^2+9)}\,dt
\end{eqnarray}$$
を
$$\begin{eqnarray}
I=\frac{\pi}{2\sqrt{2}}\int_0^{\infty}\frac{\sin x}{\ln^2 x+(\pi/2)^2}\,dx-\frac{\pi}{2e\sqrt{2}}
\end{eqnarray}$$
まで, 変形しました. 今回こそはこれを解いていきたいと思います. どうやらマイナーな定数が使われているらしいということが分かったんですが, まず, 前回の定理3を強くしていきたいと思います.
以下のように関数$\eta$を定義する. 定義域は右辺の積分が収束する範囲とする.
$$\begin{eqnarray}
\eta(\alpha,z):=\int_0^{\infty}\frac{e^{i\alpha x}}{\ln x- z}\,dx
\end{eqnarray}$$
$0\lt\alpha\in\mathbb{R}$のとき,
$$\begin{eqnarray}
\eta(\alpha, z)+\eta(-\alpha, z-i\pi)=\begin{cases}
2\pi i e^{z+i\alpha e^z},\quad (0\lt \Im z\lt \pi)\\
0,\quad (otherwise)
\end{cases}
\end{eqnarray}$$
これは前回の定理3とまったく同様なので証明は省略する.
$0\lt\Re{\alpha},\Im{\alpha}, 0\lt\beta\leq\frac{\pi}2$のとき,
$$\begin{eqnarray}
\eta(\alpha, z)-e^{i\beta}\eta(\alpha e^{i\beta}, z-i\beta)=\begin{cases}
2\pi i e^{z+i\alpha e^z},\quad (0\lt \Im z\lt \beta)\\
0,\quad (otherwise)
\end{cases}
\end{eqnarray}$$
被積分関数
$$\begin{eqnarray}
\frac{e^{i\alpha x}}{\ln x- z}
\end{eqnarray}$$
に対し, 以下のような積分路を考える.
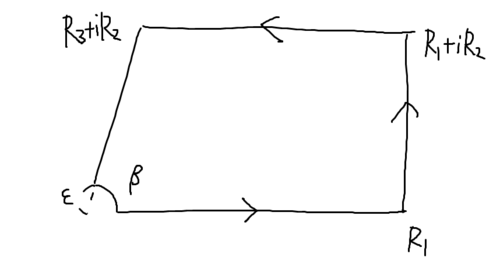 積分路
積分路
先に$R_1\to\infty$とするとして,
$$\begin{eqnarray}
\int_{R_3+iR_2}^{\infty+iR_2}\frac{e^{i\alpha x}}{\ln x- z}\,dx
\end{eqnarray}$$
が$R_2\to\infty$で$0$に収束することを示せば, あとは同様に留数定理から従う.
$$\begin{eqnarray}
\int_{R_3+iR_2}^{\infty+iR_2}\frac{e^{i\alpha x}}{\ln x- z}\,dx&=&e^{-\alpha R_2}\int_{R_3}^{\infty}\frac{e^{i\alpha x}}{\ln(x+iR_2)-z}\,dx
\end{eqnarray}$$
$0\lt\Im{\alpha}$ならば積分は収束し, $R_2\to\infty$のとき, $0$に収束する. また$0\lt\Re{\alpha}$より, $e^{-\alpha R_2}$も$0$に収束する. よって, 定理は示された.
$0\lt \alpha\in\mathbb{R}$のとき,
$$\begin{eqnarray}
\int_0^{\infty}\frac{\sin\alpha x}{\ln^2x+(\pi/2)^2}\,dx=\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2x+\pi^2}\,dx+e^{-\alpha}
\end{eqnarray}$$
定理1で$z=\frac{i\pi}{2}$として,
$$\begin{eqnarray}
\int_0^{\infty}\frac{\ln x\cos\alpha x-\frac{\pi}{2}\sin\alpha x}{\ln^2x+(\pi/2)^2}\,dx=-\pi e^{-\alpha}
\end{eqnarray}$$
また, 定理2で$\beta=\frac{\pi}{2},z=-\frac{i\pi}{2}$として, その実部をとって,
$$\begin{eqnarray}
\int_0^{\infty}\frac{\ln x\cos\alpha x+\frac{\pi}{2}\sin\alpha x}{\ln^2 x+(\pi/2)^2}\,dx=\pi\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+\pi^2}\,dx
\end{eqnarray}$$
2つ目の式から1つ目の式を引くことにより, 定理を得る.
ここで, 補題を用意しよう, と思ったんですが, 以下は証明ができなかったので予想としておいておきます.
$0\lt \alpha\in\mathbb{R}$,$\beta\in\mathbb{R}$のとき,
$$\begin{eqnarray}
\int_0^{\infty}\int_1^{\infty}x^{-y}e^{-\alpha x}\sin \beta y\,dxdy&=&\int_1^{\infty}\int_0^{\infty}x^{-y}e^{-\alpha x}\sin \beta y\,dydx\\
\int_0^{\infty}\int_0^1x^{y}e^{-\alpha x}\sin \beta y\,dxdy&=&\int_0^1\int_0^{\infty}x^{y}e^{-\alpha x}\sin \beta y\,dydx
\end{eqnarray}$$
予想が成立するならば, $0\lt \alpha\in\mathbb{R}$,$n\in \mathbb{N}$のとき,
$$\begin{eqnarray}
\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+(n\pi)^2}\,dx=\frac 1n\int_0^{\infty}\frac{\alpha^{x-1}}{\Gamma(x)}\frac{\sin n\pi x}{\sin\pi x}\,dx+\frac{(-1)^n}{n}e^{(-1)^{n-1}\alpha}
\end{eqnarray}$$
まず, よく知られたラプラス変換により,
$$\begin{eqnarray}
&&\frac 1{n\pi}\int_0^{\infty}x^{-y}\sin n\pi y\,dy=\frac{1}{\ln^2 x+(n\pi)^2},\quad (1\lt x)\\
&&\frac 1{n\pi}\int_0^{\infty}x^{y}\sin n\pi y\,dy=\frac{1}{\ln^2 x+(n\pi)^2},\quad (0\lt x\lt 1)\\
\end{eqnarray}$$
よって,
$$\begin{eqnarray}
&&\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+(n\pi)^2}\,dx\\
&=&\int_0^1\frac{e^{-\alpha x}}{\ln^2 x+(n\pi)^2}\,dx+\int_1^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+(n\pi)^2}\,dx\\
&=&\frac 1{n\pi}\left(\int_0^1\int_0^{\infty}x^{y}e^{-\alpha x}\sin n\pi y\,dydx+\int_1^{\infty}\int_0^{\infty}x^{-y}e^{-\alpha x}\sin n\pi y\,dydx\right)
\end{eqnarray}$$
ここで, 予想の式を用いると,
$$\begin{eqnarray}
&&\int_0^1\int_0^{\infty}x^{y}e^{-\alpha x}\sin n\pi y\,dydx+\int_1^{\infty}\int_0^{\infty}x^{-y}e^{-\alpha x}\sin n\pi y\,dydx\\
&=&\int_0^{\infty}\int_0^1x^{y}e^{-\alpha x}\sin n\pi y\,dxdy+\int_0^{\infty}\int_1^{\infty}x^{-y}e^{-\alpha x}\sin n\pi y\,dxdy
\end{eqnarray}$$
ここで, $0\lt y$に対し,
$$\begin{eqnarray}
\int_0^1x^ye^{-\alpha x}\,dx&=&\sum_{0\leq r}\frac{(-\alpha)^r}{r!(r+y+1)}\\
\int_1^{\infty}x^{-y}e^{-\alpha x}\,dx&=&\alpha^{y-1}\Gamma(1-y)-\sum_{0\leq r}\frac{(-\alpha)^r}{r!(r-y+1)}
\end{eqnarray}$$
であるから,
$$\begin{eqnarray}
&&\int_0^{\infty}\int_0^1x^{y}e^{-\alpha x}\sin n\pi y\,dxdy+\int_0^{\infty}\int_1^{\infty}x^{-y}e^{-\alpha x}\sin n\pi y\,dxdy\\
&=&\int_0^{\infty}\sum_{0\leq r}\frac{(-\alpha)^r}{r!(r+y+1)}\sin n\pi y\,dy+\int_0^{\infty}\left(\alpha^{y-1}\Gamma(1-y)-\sum_{0\leq r}\frac{(-\alpha)^r}{r!(r-y+1)}\right)\sin n\pi y\,dy\\
&=&\int_{r+1}^{\infty}\sum_{0\leq r}\frac{(-1)^{(r+1)n}(-\alpha)^r}{r!}\frac{\sin n\pi y}{y}\,dy+\int_{-\infty}^{r+1}\sum_{0\leq r}\frac{(-1)^{(r+1)n}(-\alpha)^r}{r!}\frac{\sin n\pi y}y\,dy\\
&+&\int_0^{\infty}\alpha^{y-1}\Gamma(1-y)\sin n\pi y\,dy\\
&=&(-1)^n\int_{-\infty}^{\infty}\frac{\sin n\pi y}{y}\,dy\sum_{0\leq r}\frac{((-1)^{n-1}\alpha)^r}{r!}+\pi\int_0^{\infty}\frac{\alpha^{y-1}}{\Gamma(y)}\frac{\sin n\pi y}{\sin\pi y}\,dy\\
&=&\pi\int_0^{\infty}\frac{\alpha^{y-1}}{\Gamma(y)}\frac{\sin n\pi y}{\sin\pi y}\,dy+(-1)^n\pi e^{(-1)^{n-1}\alpha}
\end{eqnarray}$$
よって,
$$\begin{eqnarray}
\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+(n\pi)^2}\,dx=\frac 1n\int_0^{\infty}\frac{\alpha^{x-1}}{\Gamma(x)}\frac{\sin n\pi x}{\sin\pi x}\,dx+\frac{(-1)^n}{n}e^{(-1)^{n-1}\alpha}
\end{eqnarray}$$
さて, 定理はそろったので問題を解いていきます. 定理3において, $\alpha=1$として用いることにより,
$$\begin{eqnarray}
I&=&\frac{\pi}{2\sqrt{2}}\int_0^{\infty}\frac{\sin x}{\ln^2 x+(\pi/2)^2}\,dx-\frac{\pi}{2e\sqrt{2}}\\
&=&\frac{\pi}{2\sqrt{2}}\int_0^{\infty}\frac{e^{-x}}{\ln^2 x+\pi^2}\,dx
\end{eqnarray}$$
定理4において, 特に$n=1$として,
$$\begin{eqnarray}
\int_0^{\infty}\frac{e^{-\alpha x}}{\ln^2 x+\pi^2}\,dx=\int_0^{\infty}\frac{\alpha^{x-1}}{\Gamma(x)}\,dx-e^{\alpha}
\end{eqnarray}$$
が成り立ちます. 上の式において, $\alpha=1$として,
$$\begin{eqnarray}
\frac{\pi}{2\sqrt{2}}\int_0^{\infty}\frac{e^{-x}}{\ln^2 x+\pi^2}\,dx=\frac{\pi}{2\sqrt{2}}\left(\int_0^{\infty}\frac{1}{\Gamma(x)}\,dx-e\right)
\end{eqnarray}$$
ここで,
$$\begin{eqnarray}
F=\int_0^{\infty}\frac 1{\Gamma(x)}\,dx
\end{eqnarray}$$
はFransén–Robinson constant(
https://en.wikipedia.org/wiki/Frans%C3%A9n%E2%80%93Robinson_constant
) として知られているので(いや, この定数は知らんかったわ), それを用いて,
$$\begin{eqnarray}
I=\frac{\pi}{2\sqrt{2}}(F-e)
\end{eqnarray}$$
と表すことができました. あの予想がそもそもあってるのかはおいといて, まあまあうまくいったと思いました.
