微分するとスケールが変化する関数(f'(x)=f(ax))を考えてみたが・・・

問題

前回、$t$を実数として、$f'(x)=f(x-t)$を満たす実関数を考えてみました。
一般解は求めることができなかったものの、$f(x)$が$\mathbb{R}$で解析的と仮定しても任意定数が無限に必要でした。
さらに、解析的でない関数もいろいろ考えられることがわかりました(前回記事内コメント欄参照)。

今回は$f'(x)=f(ax)$を考えてみましたが、やはり一般解はわかりませんでした。。。
(もちろん、WolframAlphaも求めてくれません。)
それどころか、$a$の値によっては、定数関数$f(x)=0$以外の特殊解がさっぱりわからないものまで・・・

一旦、わかる範囲のことを以下に書きます。

$f(x)$は微分可能なので、$f(ax)$も微分可能で、したがって$f'(x)$も微分可能です。
両辺微分して$f''(x)=af'(ax)$となり、$f'(ax)$も微分可能なので、$f''(x)$も微分可能です。
同様に繰り返せば、$f(x)$は無限回微分可能です。

具体的に一般解が求まる場合

$a=0$のとき

このときは、方程式は$f'(x)=f(0)\ (定数)$となるので、両辺を積分し、
$f(x)=f(0)x+C\ (C:定数)$となりますが、
$x=0$を代入すると$f(0)=C$になるので、
$f(x)=C(x+1)\ (C:定数)$が一般解となります。
これ、スケール変化というか、ただの$1$次関数です・・・

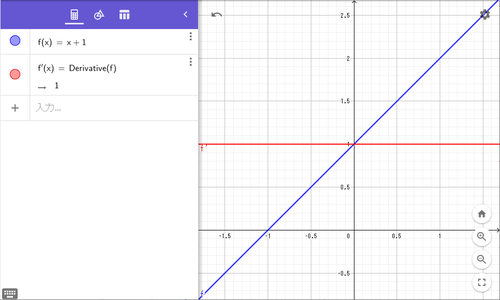a=0

$a=1$のとき

これはスケールが変わらないやつです。
このときは、$f'(x)=f(x)$となり、微分方程式の中でも一番基本的な変数分離の問題になります。
定数関数$f(x)=0$が特殊解になるのは明らかなので、
$f(x)\ne0$を仮定して、両辺$f(x)$で割ると、
$\frac{f'(x)}{f(x)}=1$
両辺積分して
$\log|f(x)|=x+c\ (c:定数)$
よって、$f(x)=\pm e^{x+c}$
$f(x)=0$の場合も含めて定数を置き換えると
$f(x)=Ce^x\ (C:定数)$という一般解が得られます。

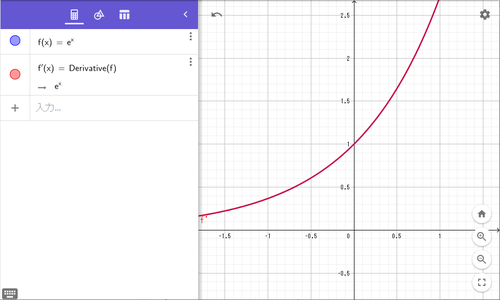a=1

$a=-1$のとき

このときは、$f'(x)=f(-x)$となりますが、 この微分方程式について、以前記事を作っています。
ざっくり説明すると、$f(x)$は$2$階微分可能なので、
$f'(x)=f(-x)$を両辺微分して、
$f''(x)=-f'(-x)=-f(x)$
これは$2$階斉次微分方程式で、解は
$f(x)=A\cos(x)+B\sin(x)\ (A,B:定数)$となりますが、
これが$f'(x)=f(-x)$を満たすためには$A=B$でなければならず、結局は
$f(x)=C(\cos(x)+\sin(x))\ (C:定数)$が一般解であることがわかります。

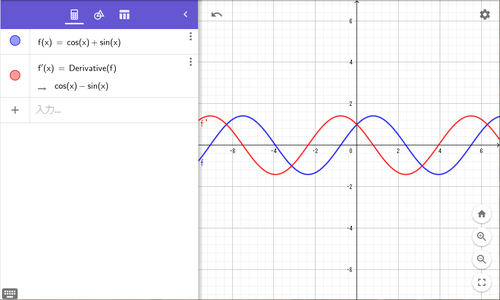a=-1

一般解がよくわからなかったやつについて解析的な解を調べる

$a=-1,0,1$以外の場合はよくわかりませんでした。
ひとまず、$f(x)$は無限回微分可能なので、$f(x)$は解析的だと仮定して解を調べてみます。

$f'(0),f''(0),f'''(0),\cdots$を求めます。
$f'(x)=f(ax)$より、$f'(0)=f(0)$
$f''(x)=af'(ax)=af(a^2x)$より、$f''(0)=af(0)$
$f'''(x)=a^2f''(ax)=a^3f(a^3x)$より、$f'''(0)=a^3f(0)$
$f^{(4)}(x)=a^3f'''(ax)=a^6f(a^4x)$より、$f^{(4)}(0)=a^6f(0)$
繰り返すと、$f^{(n)}(x)=a^{\frac{n(n-1)}{2}}f(a^nx)$より、$f^{(n)}(0)=a^{\frac{n(n-1)}{2}}f(0)$です。

したがって、
$\displaystyle f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n=f(0)\sum_{n=0}^{\infty}\frac{a^{\frac{n(n-1)}{2}}}{n!}x^n$
となります。($n=0,x=0$では$x^n=1$、$a=0,n=0,1$では$a^{\frac{n(n-1)}{2}}=1$と約束します。)

$|a|\leqq 1$のとき

$|a|\leqq 1$のとき、ダランベールの判定法から、$\displaystyle \sum_{n=0}^{\infty}\frac{a^{\frac{n(n-1)}{2}}}{n!}x^n$は収束します。
$f(0)=C$とすると、
$\displaystyle f(x)=C\sum_{n=0}^{\infty}\frac{a^{\frac{n(n-1)}{2}}}{n!}x^n\ (C:定数)$が解になります。

この冪級数を何かの初等関数や特殊関数で表せないのかな？と思ってWolframAlphaで調べましたが、何も出てきませんでした。残念・・・
さらに、$f(x)$が解析的であることを仮定してこの解が得られているので、他に非解析的な解がある可能性があります。

a=1/2

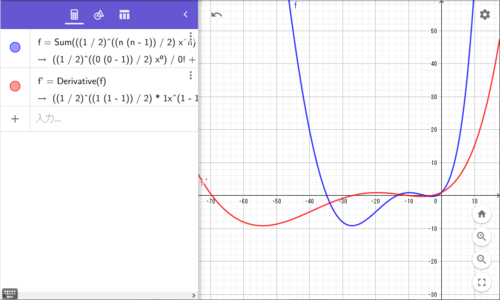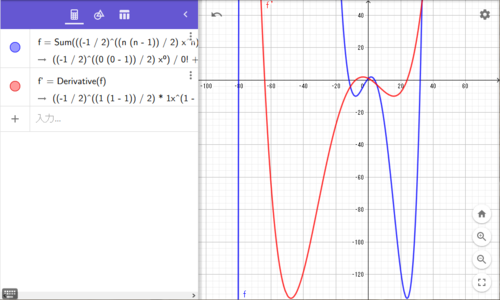a=-1/2

$|a|>1$のとき

$|a|>1$のとき、
$f(0)=0$ならば、$f(x)=0$が出ますが、
$f(0)\ne 0$のときは$\displaystyle \sum_{n=0}^{\infty}\frac{a^{\frac{n(n-1)}{2}}}{n!}x^n$の収束半径が$0$になります。
つまり、$f'(x)=f(ax)$を満たす解析的な解は$f(x)=0$しかありません。

非解析的な解ってあるんだろうか・・・

$0<|a|<1$または$|a|>1$のときは非解析的な解がある可能性があります。
$x=0$で冪級数展開できない解を構成するには、色々と変なことを考える必要が出てくるわけです。

$a=2$のときの非解析的な解を構成しようとしてみた

とりあえず、$a=2$としましょう。
まず、$[1,2]$の区間で、無限回微分可能関数$f(x)$を決めます。
すると、$[1,2]$で$f'(x)$が決まり、$f(2x)$が決まり、
$[2,4]$で$f(x)$が決まります。
同様に、$[4,8]$,$[8,16]$,$\cdots$と決まっていき、$[1,+\infty)$まで決まります。
逆に積分を考えることで、$[\frac{1}{2},1]$,$[\frac{1}{4},\frac{1}{2}]$,$\cdots$も決まります。
最終的に$(0,+\infty)$の範囲まで決定できます。
同じように$[-2,-1]$の区間で$f(x)$を決めることで、$(-\infty,0)$も決まり、$f(0)$は両側の極限で定義すればいいのです。
ただし、$x=\cdots,-4,-2,-1,-\frac{1}{2},-\frac{1}{4},\cdots,0,\cdots,\frac{1}{4},\frac{1}{2},1,2,4,\cdots$でも無限回微分可能になるように、いい感じにくっつける必要があります。
そのため、どう構成しようかと悩んでるのが現状です。

その他わかること

(証明)
まず、閉区間$[0,1]$において、恒等的に$f(x)=0$であることを背理法で証明します。

$f(x)$が閉区間$[0,1]$で$f(x)\not\equiv0$と仮定します。
すると、$f(s)\ne 0$となる$s\in(0,1]$がありますが、
$f'(x)=f(ax)$の解$f(x)$に対して、定数倍$Cf(x)$、特に$-1$倍の$-f(x)$もまた解になっているので、
$f(s)>0$としても一般性は失いません。

次に、区間$(0,s]$の部分集合で、$f(x)=f(s)$を満たす$x$の集合を用意します。
この集合$\{x\in(0,s]|f(x)=f(s)\}$は、必ず$s$を要素に持つので空集合ではありません。

$t=\inf\{x\in(0,s]|f(x)=f(s)\}$とすると、
$f(x)$は連続なので、$t>0$です。
さらに、$0< u< t\Rightarrow f(u)< f(t)$を満たします。

さて、
$f'(x)=f(ax)$は両辺積分して、
$f(x)=f(0)+\frac{1}{a}\int_{0}^{ax}f(u)du$と表すことができます。
ここでは$f(0)=0$なので、$f(x)=\frac{1}{a}\int_{0}^{ax}f(u)du$となります。

$f(t)$を不等式で評価すると、
\begin{align} f(t) & = \frac{1}{a}\int_{0}^{at} f(u) du \\ & < \frac{1}{a}\int_{0}^{at} f(t) du\ (\leftarrow f(u)< f(t))\\ & = \frac{1}{a}\times atf(t) \\ & = tf(t) \\ & \leqq f(t)\ (\leftarrow t\leqq1) \end{align}
つまり、$f(t)< f(t)$となって矛盾します。

したがって、閉区間$[0,1]$において、恒等的に$f(x)=0$です。

続いて、範囲を広げて$[0,\infty)$上の$x$で$f(x)=0$になることを証明します。

$f(x)=\frac{1}{a}\int_{0}^{ax}f(u)du$の$ax$を改めて$x$とすることで、
$f(\frac{x}{a})=\frac{1}{a}\int_{0}^{x}f(u)du$となります。

$x\in[0,1]$ならば、$\int_{0}^{x}f(u)du=0$なので、$f(\frac{x}{a})=0$です。
これは、$x\in[0,\frac{1}{a}]$において$f(x)=0$であることを意味します。

変数の置き換えを繰り返すことで、$f(x)=0$が言える範囲が$[0,\frac{1}{a^2}],[0,\frac{1}{a^3}],[0,\frac{1}{a^4}],\cdots$と広がり、
最終的に$[0,\infty)$上の$x$で$f(x)=0$になることがわかります。

さいごに

自分の予想としては、
$f(0)=0$となる非解析的な解はなく、
$f(0)\ne 0$ならば$a\ne -1,0,1$のときに非解析的な解がある
と思っています。
どなたかご存じの方は教えてください。