Grapharyに収録されているグラフを解説する(ID11~20)
前回の記事 の続きです。今回はID11~20を解説します。
前回よりも複雑な関数が多いので、記事の文章量が多くなっています。
元サイト(Graphary): https://teth-main.github.io/Graphary/
相互リンク
一覧
ID11: 逆三角関数を用いて表された半径が1の円
式: $ \sin^{-1}(|x|) + \sin^{-1}(|y|) = \frac{\pi}{2} $
難易度: ★☆☆☆☆
$ x $と$ y $にはともに絶対値記号がついているので、第1象限だけ考えればよいです。
また、$ \sin^{-1}{x} $の定義域は$ -1 \leq x \leq 1 $なので、第1象限でグラフが描画される範囲は$ x \leq 1, y \leq 1 $に制限されます。
残りはこれらの図を見てください。
![!FORMULA[6][923556884][0]が円内にあるとき、!FORMULA[7][-1178649829][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FBWWHWRVaHLcE5jvOwRjk.png?alt=media) $ (x, y) $が円内にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} < \frac{\pi}{2} $
$ (x, y) $が円内にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} < \frac{\pi}{2} $
![!FORMULA[8][923556884][0]が円周上にあるとき、!FORMULA[9][174659868][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F62XGh6dglb2skW1pByyl.png?alt=media) $ (x, y) $が円周上にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} = \frac{\pi}{2} $
$ (x, y) $が円周上にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} = \frac{\pi}{2} $
![!FORMULA[10][923556884][0]が円周上にあるとき、!FORMULA[11][1527969565][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FU5fjIR7nKxV4zbH0hRjP.png?alt=media) $ (x, y) $が円周上にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} > \frac{\pi}{2} $
$ (x, y) $が円周上にあるとき、$ {\color{blue}\sin^{-1}{x}} + {\color{orange}\sin^{-1}{y}} > \frac{\pi}{2} $
ID12: 1辺が2の正三角形
式: $ \left|\left|x\right|+\frac{2}{\sqrt{3}}y\right|+\left|x\right|=1 $
難易度: ★★★☆☆
全ての$ x $に絶対値記号がついているので、$ x \geq 0 $の範囲で考えればよいことが分かります。
ところで、絶対値とは何でしょう?
絶対値とは、その数と$ 0 $との距離のことです。
$ x $と$ y $は実数なので、数直線上での距離を考えることになります。
また、$ \left| a - b \right| $は、数直線上での$ a $と$ b $の距離といえます。
さて、もう一度元の式を見てみましょう。$ x \geq 0 $のとき、$ \left|x\right| = x $なので元の式はこのように書けます。
$ \left|x+\frac{2}{\sqrt{3}}y\right|+\left|x\right|=1 $
右側の絶対値記号を外さなかった理由は次に行う変形を見るとわかります。
$ \left|x - \left(-\frac{2}{\sqrt{3}}y\right) \right| + \left|x - 0\right| = 1 $
すなわち、$ y $を固定したとき$ x $座標の値は「数直線上に$ 3 $点$ A\left(-\frac{2}{\sqrt{3}}y\right), B(0), P(x) $を取ったとき、$ AP + BP = 1 $になる点$ P $の座標」であることがわかります。
そこで、$ y $を固定するごとに$ A $と$ B $がどこに位置するか調べるために、補助線を引いてみましょう。
![緑が!FORMULA[34][34263561][0]の位置、青が!FORMULA[35][34264522][0]の位置](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F6nfsez9ZMicgE2IiJTDO.png?alt=media) 緑が$ A $の位置、青が$ B $の位置
緑が$ A $の位置、青が$ B $の位置
$ y \geq 0 $のときは、$ P $は必ず$ A $と$ B $の右にあります。
$ y < 0 $で$ P $が$ A $と$ B $の間にあるとき、$ AP + BP = AB $なのでこれが条件を満たすのは$ AB = 1 $のときだけです。これは三角形の下の辺に対応します。
$ y < 0 $で$ P $が$ A $の右にあっても、$ PB \geq AB > 1 $であれば$ AP + BP > 1 $になるので条件を満たしません。
よって、$ y \geq -\frac{\sqrt{3}}{2} $でかつ$ P $が$ A $と$ B $の両方より右にあるときだけを考えればよいことが分かります。
$ P(x, y) $とおくと、
$ AP + BP = \left(x - \left( -\frac{2}{\sqrt{3}}y \right)\right) + (x - 0) = 2x + \frac{2}{\sqrt{3}}y $
なので、
$ AP + BP = 1 $
であることから
$ x = \frac{1}{2} - \frac{1}{\sqrt{3}} y $
であることがわかります。
これを$ y $について整理すると、
$ y = - \sqrt{3}x + \frac{\sqrt{3}}{2} $
となります。
$ x < 0 $(左の辺)に対応する式は$ y = \sqrt{3}x + \frac{\sqrt{3}}{2} $です。
これをもとに三角形の$ 3 $つの頂点の座標を計算すると、
$ \left(0, \frac{\sqrt{3}}{2}\right), \left(1, -\frac{\sqrt{3}}{2}\right), \left(-1, -\frac{\sqrt{3}}{2}\right) $
となります。
これら$ 3 $つの頂点の距離は全て$ 2 $なので、この三角形が正三角形であることがわかりました。
ID13: リボン
式: $ \left|2\left|x\right|-\left|y\right|-2\right|+\left|y\right|=2 $
難易度: ★★★☆☆
$ x $と$ y $に絶対値記号がついているので$ x, y \geq 0 $のときだけ考えると$ |2x-y-2|+|y|=2 $となりこれを変形すると$ |y-(2x-2)|+|y-0|=2 $となるのでID12と同じようにできます。
・・・だけでは面白くないので、いちおう別解法も載せておきます。オーソドックスでつまらない解法ですが、基本に忠実に解くこともできるという意味で載せました。
解法
与式は$ x \rightarrow -x, y \rightarrow -y $と置換しても左辺は変わらないので第1象限だけ考えればよい。この範囲で与式は
$ | 2x - y - 2 | + y = 2 $
となるので、$ 2x - y - 2 $の符号で場合分けする。
(i) $ 2x - y - 2 \geq 0 $すなわち$ y \leq 2x - 2 $のとき
与式は$ (2x - y - 2) + y = 2 $すなわち$ 2x - 2 = 2 $となるので、これを解いて$ x = 2 $を得る。
$ y \geq 0, y \leq 2x - 2 $であるから、この範囲のグラフは$ x = 2 (0 \leq y \leq 2) $である。
(ii) $ 2x - y - 2 < 0 $すなわち$ y > 2x - 2 $のとき
与式は$ -(2x - y - 2) + y = 2 $すなわち$ -2x + 2y + 2 = 2 $となるので、これを解いて$ y = x $を得る。
$ x \geq 0, y > 2x - 2 $であるから、この範囲のグラフは$ y = x (0 \leq x < 2) $である。
これらを合わせると、次のグラフが得られる:
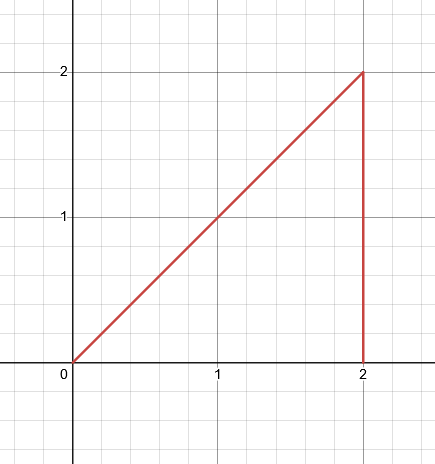 第1象限の範囲でのグラフ
第1象限の範囲でのグラフ
これに$ x $軸と$ y $軸とその両方に関して反転させたものを追加することで、座標平面全体でのグラフが得られる:
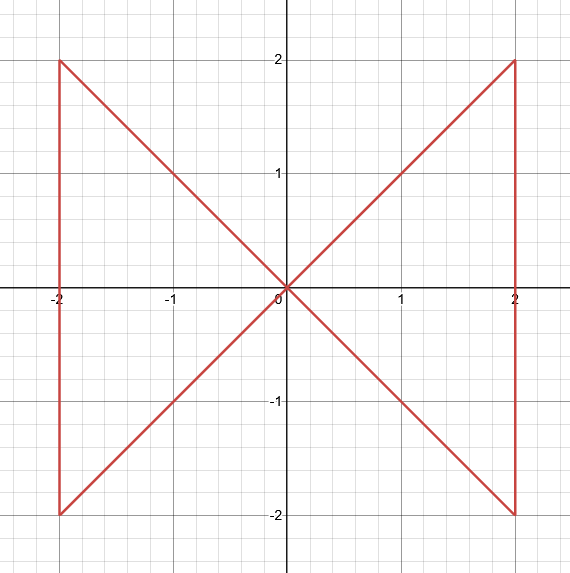 座標平面全体でのグラフ
座標平面全体でのグラフ
ID14: 市松模様
式: $ \frac{\sin\left(x\right)}{\cos\left(y\right)}>0 $
難易度: ★☆☆☆☆
$ \sin\left(x\right) $と$ \cos\left(y\right) $が同符号である領域に色がつきます。$ \sin $も$ \cos $も周期関数なので周期的な模様になります。
$ \sin\left(x\right) = 0 $と$ \cos\left(y\right) = 0 $が境界線になり、境界線を越えるごとに片方だけ符号が反転するので色が入れ替わります。境界線の交点を通った場合は縦と横の境界線を同時に通ったとみなし、$ 2 $回色が入れ替わって元と同じ色になります。
ところで、Grapharyの描画では縦と横で境界線の描かれ方が違うことに気づいたでしょうか? 縦線は点線で描かれていますが、横線は描かれていません。
これはDesmosのデフォルトの設定で、「不等式の両辺が同じになるときの境界線は点線で描く」ようになっているからです。縦線は$ \sin\left(x\right) = 0 $に対応し、このとき$ \frac{\sin\left(x\right)}{\cos\left(y\right)} = 0 $になるため点線が描かれています。
一方、横線は$ \cos\left(y\right) = 0 $に対応しますが、このとき$ \frac{\sin\left(x\right)}{\cos\left(y\right)} $は分母がゼロになるため値が定義されません。そのため、Desmosでは点線が描かれず、突然色のついた領域が終わるように描かれています。
受験数学ではこれらを区別せず、境界は全て実線で表記して図の近くに「境界線を含まない」と記述するのが一般的です。
ID15: ゼロの形をした少し四角めな円
式: $ \left(\cos t,2\sqrt[3]{\sin t}\right) $
難易度: ★★☆☆☆
$ -1 \leq x \leq 1 $のとき、$ |\sqrt[3]{x}| \geq |x| $が成り立ちます。そのため、点$ (1, 0) $付近では曲線が楕円より外側を通り、左右の端がより平坦になります。また、$ 1 - |\sqrt[3]{x}| \leq 1 - |x| $が成り立つので、同じように考えることで上下の端がより平坦になります。
![赤:!FORMULA[109][373853916][0] 青: !FORMULA[110][-1111375613][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FLBiPnkdH1mTDH2oL64TN.png?alt=media) 赤:$ y = 2\sin{x} $ 青: $ y = 2\sqrt[3]{\sin{x}} $
赤:$ y = 2\sin{x} $ 青: $ y = 2\sqrt[3]{\sin{x}} $
ID16: 1枚の花弁の花
式: $ r=2+\frac{\sin5\theta+\cos10\theta}{2} $
難易度: ★★★★☆
まず、三角関数の中身が全て$ 5 \theta $の倍数なのでグラフが$ 1 $周する間に同じ形が$ 5 $回繰り返されることがわかります。
そこで、$ \varphi = 5 \theta $とおいて、$ f(\varphi) = 2+\frac{\sin{\varphi}+\cos{2\varphi}}{2} $について調べましょう。$ 0 \leq \theta < \frac{2\pi}{5} $、すなわち$ 0 \leq \varphi < 2\pi $の範囲での挙動を調べれば、これを$ 5 $回繰り返すことで元の式のグラフが描けます。
この挙動を調べるために、$ f(\varphi) $を微分します。$ f(\varphi) $を微分した結果は次のように変形できます。
\begin{align*} & f'(\varphi) \\ =\,& \frac{\cos{\varphi} - 2\sin{2\varphi}}{2} \\ =\,& \frac{\cos{\varphi} - 4\sin{\varphi}\cos{\varphi}}{2} \\ =\,& \frac{1}{2} \cos{\varphi} (1 - 4\sin{\varphi}) \end{align*}
したがって、$ 1 - 4\sin{\varphi} = 0 $となる$ \varphi \in [0, 2\pi] $を$ \alpha, \beta (\alpha < \beta) $とすると、$ 0 < \alpha < \frac{\pi}{2} < \beta < \pi $であることから、$ 0 \leq \varphi < 2\pi $での増減表は次のようになります:
| $ \varphi $ | $ 0 $ | $ \cdots $ | $ \alpha $ | $ \cdots $ | $ \frac{\pi}{2} $ | $ \cdots $ | $ \beta $ | $ \cdots $ | $ \frac{3\pi}{2} $ | $ \cdots $ | $ 2\pi $ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $ f'(\varphi) $ | $ + $ | $ + $ | $ 0 $ | $ - $ | $ 0 $ | $ + $ | $ 0 $ | $ - $ | $ 0 $ | $ + $ | $ + $ |
| $ f(\varphi) $ | $ \frac{5}{2} $ | $ \nearrow $ | 極大 | $ \searrow $ | $ 2 $ | $ \nearrow $ | 極大 | $ \searrow $ | $ 1 $ | $ \nearrow $ | $ \frac{5}{2} $ |
ここで書いた2つの「極大」ですが、これらは$ \beta = \pi - \alpha $に注意すると
\begin{align*} & f(\beta) \\ =\,& 2+\frac{\sin{\beta}+\cos{2\beta}}{2} \\ =\,& 2+\frac{\sin{\alpha}+\cos{2(\pi - \alpha)}}{2} \\ =\,& 2+\frac{\sin{\alpha}+\cos{(2\pi - 2\alpha)}}{2} \\ =\,& 2+\frac{\sin{\alpha}+\cos{2\alpha}}{2} \\ =\,& f(\alpha) \end{align*}
であることから、これらは等しいことが分かります。よって、$ y = f(\varphi) $のグラフは次のようになることが分かります。
![!FORMULA[165][1538080751][0]のグラフ(横軸は!FORMULA[166][2010767822][0])](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fe55H2WNS9TSFHdsgO0ir.png?alt=media) $ y = f(\varphi) $のグラフ(横軸は$ \varphi $)
$ y = f(\varphi) $のグラフ(横軸は$ \varphi $)
あとは、これを$ 5 $周期分並べて丸めることで元の式のグラフが得られます。
・・・と書いたものの、微分を使う説明は「グラフの形状から式を導く」ことに適していないので、厳密ではないですが直感的な説明も書きます。参考としてどうぞ。
直感的な説明
$ \sin{\varphi} $と$ \cos{2\varphi} $のグラフを考えると、片方の傾きがもう片方の$ -1 $倍になるところが、$ f'(\varphi) = 0 $になる点です。
そのような点はグラフから$ 0 $と$ \frac{\pi}{4} $の間、$ \frac{\pi}{2} $、$ \frac{3\pi}{4} $と$ \pi $の間、そして$ \frac{3\pi}{2} $にあることが分かります。実際に、それらが上で求めた極大・極小を取る$ \varphi $の値に対応します。
グラフは$ \frac{\pi}{2} $に関して左右対称であることから、$ 2 $つの極大値が同じ値であることがわかります。
また、$ \frac{\pi}{2} $と$ \frac{3\pi}{2} $での値も、それぞれのグラフから読み取ることで計算できます。
これらの考察により、図5と同じ形状のグラフを得ることができます。
(これ以外の極値がないことを厳密に確認するためには微分が必要です)
![赤:!FORMULA[183][-916361858][0] 青:!FORMULA[184][920858937][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FR6svCGsOF7pHnzXx5SsH.png?alt=media) 赤:$ \sin{\varphi} $ 青:$ \cos{2\varphi} $
赤:$ \sin{\varphi} $ 青:$ \cos{2\varphi} $
ID17: おしべ付きの5枚花弁
式: $ r=1+2\sin5\theta $
難易度: ★★★☆☆
式はID16より単純ですが、$ r < 0 $になることがあるのが難しい点です。
それ以外は特に言うことも無いので、自作のDesmosツールを紹介します。
極座標ビジュアライザ
https://www.desmos.com/calculator/apyekeagic?lang=ja
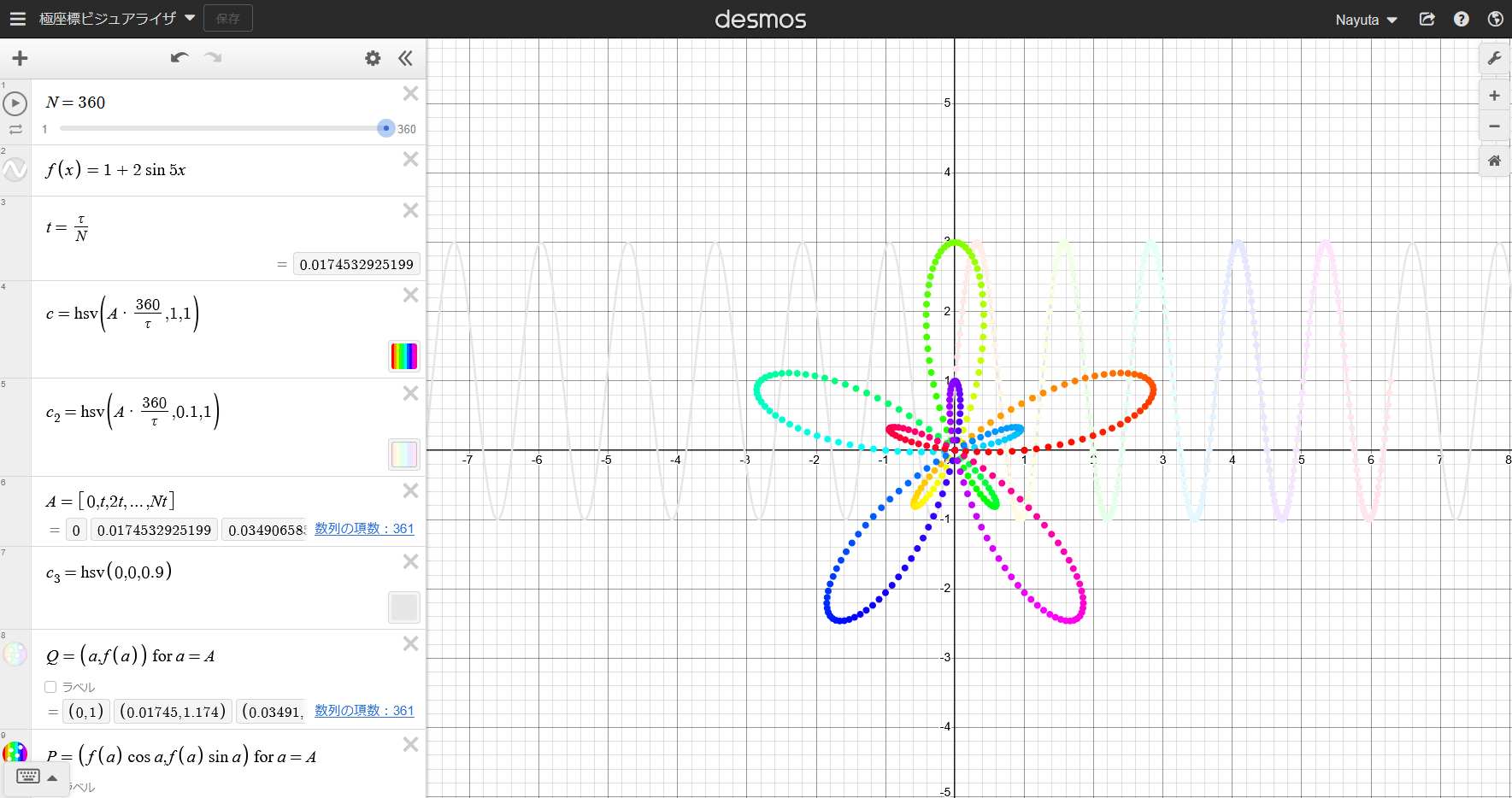 極座標ビジュアライザの画面
極座標ビジュアライザの画面
$ r = f(\theta) $に対して、「$ f(x) = $」以下に$ f(\theta) $の$ \theta $を$ x $に変えたものを入力してください。直交座標での薄い$ y = f(x) $のグラフと、極座標での濃い$ r = f(\theta) $のグラフが表示されます。
色は$ \theta $に対応しており、$ \theta $が$ 1 $周すると色相環も$ 1 $周するように色が割り振られています。また、薄いグラフでも$ 0 \leq x \leq 2\pi $の範囲で色が着くようになっています。
一番上にある$ N $は描画する点の個数で、値が大きいほど細かく描画されます。点がまばらになって線が見づらい場合は$ N $を大きくしてください。
このように図示すると、$ r < 0 $のときにどこに点が描画されるかが分かりやすいと思います。
ID18: ハート
式: $ 9x^{2}+\left(4y-5\cos\left(\left|x\right|-1\right)\right)^{2}=9 $
難易度: ★★★☆☆
$ (\text{定数})x^2+(y\text{に関する}1\text{次式})^2=(\text{定数}) $の形なので、楕円をベースにしていそうです。
実際に、楕円の標準形に近づけてみましょう。
\begin{align*} 9x^{2}+\left(4y-5\cos\left(\left|x\right|-1\right)\right)^{2} &= 9 \\ x^{2}+\frac{\left(4y-5\cos\left(\left|x\right|-1\right)\right)^{2}}{3^2} &= 1 \\ x^{2}+\frac{\left(y-\frac{5}{4}\cos\left(\left|x\right|-1\right)\right)^{2}}{\left(\frac{3}{4}\right)^2} &= 1 \\ \frac{x^2}{1^2}+\frac{\left(y-\frac{5}{4}\cos\left(\left|x\right|-1\right)\right)^{2}}{\left(\frac{3}{4}\right)^2} &= 1 \\ \end{align*}
最後に、$ \frac{5}{4}\cos\left(\left|x\right|-1\right)=A $とおくと、この式は
$$ \frac{x^2}{1^2}+\frac{\left(y-A\right)^{2}}{\left(\frac{3}{4}\right)^2} = 1 $$
となり、横幅$ 2 $、縦幅$ \frac{3}{2} $の楕円を$ y $軸方向にずらしたものであることがわかります。ただし、$ A $の値は$ x $に依存するので、ずらす量は$ x $ごとに異なります。
$ A $について考えると、$ -1 \leq x \leq 1 $であることから、$ x = 0 $のときが最小、$ x = \pm 1 $のときが最大であることが分かります。
$ 1 < \frac{\pi}{2} $なので、この範囲では必ず$ A > 0 $となります。
$ A $が$ x = 0 $で微分不可能であることを考えると、グラフはハート形になることが分かります。
![赤:与式 青:!FORMULA[221][1767775811][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FYuLPt0jXJcXkX1fizl5H.png?alt=media) 赤:与式 青:$ y = A(-1 \leq x \leq 1) $
赤:与式 青:$ y = A(-1 \leq x \leq 1) $
ID19: 丸みを帯びた1枚花弁の花
式: $ r=1+\sqrt{\left|\sin\frac{5}{2}\theta\right|}+\frac{\left|\sin5\theta\right|}{3} $
難易度: ★★★☆☆
ID16と同じように、$ \varphi = 5 \theta $とおきます。まずは、$ |\sin{5\theta}|=|\sin\varphi| $から調べてみましょう。
![!FORMULA[225][-1224540372][0](横軸は!FORMULA[226][2010767822][0])](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FxBYNZJd8lY0kC3jUGRlp.png?alt=media) $ y = |\sin\varphi| $(横軸は$ \varphi $)
$ y = |\sin\varphi| $(横軸は$ \varphi $)
$ \sin $と$ \cos $に絶対値をつけると、周期が半分になります。これは$ \sin(\pi + \alpha) = -\sin{\alpha}, \cos(\pi + \alpha) = -\cos{\alpha} $から従います。
では実際に、$ \sqrt{\left|\sin{\frac{\varphi}{2}}\right|}, \frac{|\sin\varphi|}{3}, r \left(= 1 + \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} + \frac{|\sin\varphi|}{3} \right) $のグラフを見てみましょう。
![赤:!FORMULA[231][-1519027473][0] 緑:!FORMULA[232][-1999585619][0] 青: !FORMULA[233][-138025524][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FWqYO2eIKVVdH5xVktuD1.png?alt=media) 赤:$ \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} $ 緑:$ \frac{|\sin\varphi|}{3} $ 青: $ r \left(= 1 + \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} + \frac{|\sin\varphi|}{3}\right) $
赤:$ \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} $ 緑:$ \frac{|\sin\varphi|}{3} $ 青: $ r \left(= 1 + \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} + \frac{|\sin\varphi|}{3}\right) $
これの$ 5 $周期分を並べて丸めることで、$ 5 $回対称の花弁ができることがわかります。また、$ \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} $が大きなへこみに対応し、$ \frac{|\sin\varphi|}{3} $が小さなへこみに対応していることもわかりますね。
ID20: 引き伸ばされた円
式: $ \left(\cos t,\sin t+\tanh\left(9\sin t\right)\right) $
難易度: ★★★★☆
$ \tanh $という見慣れない関数が出てきましたが、定義は
$$ \tanh{x} = \frac{\sinh{x}}{\cosh{x}} $$
です。
ではさっそく、$ \tanh $のグラフを見てみましょう。
![!FORMULA[242][-1054051609][0]のグラフ](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FBxgHFTV4dV6k9Esrk5db.png?alt=media) $ y = \tanh{x} $のグラフ
$ y = \tanh{x} $のグラフ
$ \tan $とは違って、グラフが横に伸びるのが特徴です。
また、$ x \leq -3 $では$ \tanh{x} \approx -1 $、$ x \geq 3 $では$ \tanh{x} \approx 1 $になっていますね。このグラフアートでは、この性質が利用されています。
この性質は機械学習においても利用されることがあります。
改めて元の式を見てみると、$ \tanh $の中身が$ 9\sin{t} $であり、大部分で$ -1 $または$ 1 $に近い値を取ることが分かります。実際に、それを使ってグラフを近似してみましょう。
$ x = \cos{t}, y = \sin t+\tanh\left(9\sin t\right) $とします。
- $ \sin{t} \geq \frac{1}{3} $のとき: $ \tanh{(9\sin{t})} \approx 1 $なので$ y \approx \sin{t} + 1 $となり、単位円の上部を$ y $軸方向に$ 1 $ずらした形で近似されます。
- $ \sin{t} \leq -\frac{1}{3} $のとき: $ \tanh{(9\sin{t})} \approx -1 $なので$ y \approx \sin{t} - 1 $となり、単位円の下部を$ y $軸方向に$ -1 $ずらした形で近似されます。
- $ -\frac{1}{3} < \sin{t} < \frac{1}{3} $のとき: $ \frac{\sqrt{8}}{3} < |\cos{t}| < 1 $なのでグラフの左右の部分に対応します。$ x $と$ y $はともに連続関数なので、$ \sin{t} \geq \frac{1}{3} $と$ \sin{t} \leq -\frac{1}{3} $に対応する曲線の間を線で結ぶことが分かります。$ \frac{\sqrt{8}}{3} > 0.94 $なので、この間の線はほぼ垂直であることが分かります。
これらを合わせると、Grapharyにある単位円を引き伸ばしたようなグラフが得られます。