Grapharyに収録されているグラフを解説する(ID21～30)

前回の記事 の続きです。今回はID21～30を解説します。

元サイト(Graphary): https://teth-main.github.io/Graphary/

相互リンク

• ID1～10
• ID11～20
• ID21～30 ←いまここ
• ID31～41

略記

円周と半径の比、すなわち$ 2 \pi $を記号$ \tau $で表すことにします。

一覧

ID21: 正n角形

式: $ \frac{\left(\cos t,\sin t\right)}{\cos\left(\frac{\cos^{-1}\left(\cos nt\right)}{n}\right)} $
難易度: ★★★☆☆

式の表記について

Desmosでは、$ \frac{(A, B)}{C} $で$ \left(\frac{A}{C}, \frac{B}{C} \right) $が表せる仕様になっています。たとえば、$ \frac{(1, 2)}{3} $は点$ \left(\frac{1}{3}, \frac{2}{3} \right) $を表します。

解説

このグラフは、単位円に外接する正$ n $角形になります。そのことを念頭に、まずは$ 0 \leq t \leq \frac{\tau}{2n} $の範囲において、座標の計算を行ってみましょう。

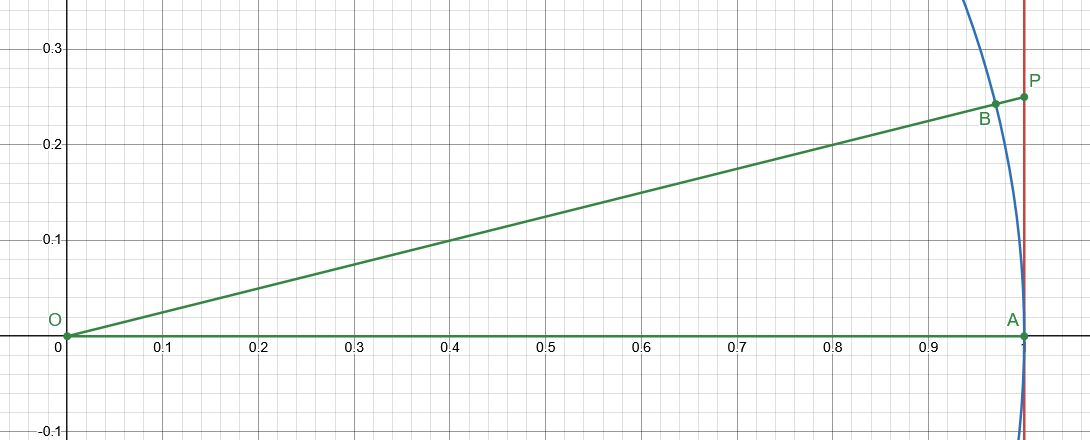
$ O(0, 0), A(1, 0) $とし、$ P $は直線$ x = 1 $上の$ y > 0 $の部分で$ \angle POA = t $を満たす点、$ B $は直線$ OP $と単位円の交点のうち$ x > 0 $である方とします。

このとき、$ OA = 1, \cos{t} = \frac{OP}{OA} $であることから、$ OP = \frac{1}{\cos{t}} $であることがわかります。
よって、$ P $の座標は$ t $を用いて

$$ \left( \frac{\cos{t}}{\cos{t}}, \frac{\sin{t}}{\cos{t}} \right) $$

と書けます。

$ 0 \leq t \leq \frac{\tau}{2n} $の範囲においてはこの分母は$ \cos{t} $ですが、正$ n $角形の各辺を$ 2 $分割したそれぞれについて考えると$ 0 \leq t \leq \tau $の範囲において分母は次のようになってほしいことが分かります。

• $ 0 \leq t \leq \frac{\tau}{2n} $のとき$ \cos{t} $
• $ \frac{\tau}{2n} \leq t \leq \frac{2\tau}{2n} $のとき$ \cos{\left(\frac{2\tau}{2n} - t\right)} $
• $ \frac{2\tau}{2n} \leq t \leq \frac{3\tau}{2n} $のとき$ \cos{\left(t - \frac{2\tau}{2n}\right)} $
• $ \frac{3\tau}{2n} \leq t \leq \frac{4\tau}{2n} $のとき$ \cos{\left(\frac{4\tau}{2n} - t\right)} $
• $ \frac{4\tau}{2n} \leq t \leq \frac{5\tau}{2n} $のとき$ \cos{\left(t - \frac{4\tau}{2n}\right)} $
• $ \hspace{35mm}\vdots $
• $ \frac{(2n-3)\tau}{2n} \leq t \leq \frac{(2n-2)\tau}{2n} $のとき$ \cos{\left(\frac{(2n-2)\tau}{2n} - t\right)} $
• $ \frac{(2n-2)\tau}{2n} \leq t \leq \frac{(2n-1)\tau}{2n} $のとき$ \cos{\left(t - \frac{(2n-2)\tau}{2n}\right)} $
• $ \frac{(2n-1)\tau}{2n} \leq t \leq \tau $のとき$ \cos{\left(\tau - t\right)} $

ここで、$ \cos $の中身を$ 0 \leq t \leq \tau $の範囲でグラフにすると、次のようになります。
(図は$ n = 7 $のとき)

この形、どこかで見ましたね。覚えていましたでしょうか? そう、ID10すなわち$ y = \arccos{(\cos{x})} $です。

$ y = \arccos(\cos{x}) $

これを縦横に$ n $分の$ 1 $にすると、元の式の$ \frac{\cos^{-1}\left(\cos nt\right)}{n} $の部分が得られます。

あとはこれを$ \cos $の中に入れて、$ ( \cos{t}, \sin{t} ) $の分母に置けば元の式の全体が得られますね。

ID29: 虚数を使った円

式: $ i^{t} $
難易度: ★☆☆☆☆

ID22の解説のために必要なので先に解説します。

Desmosの仕様

Desmosには「複素数モード」があり、これを有効にすると座標平面を複素数平面としてグラフを描くことができるようになります。

$ i^{t} $の場合は、

という問題の答えが図示されます。

解説

$ i^{t} = e^{\frac{\tau}{4}ti}.\ \ \square $

ID22: 正n角形

式: $ \frac{i^{t}}{\sqrt[n]{i^{nt}}.\operatorname{real}} $
難易度: ★★★☆☆

式の表記について

Desmosでは、複素数$ z $に対し$ z.\operatorname{real} $で$ z $の実部を表します。$ z $の虚部は$ z.\operatorname{imag} $で表します。

解説

ID21と同じものが複素数によって実現されています。

分母にある$ \sqrt[n]{i^{nt}} $は$ \sqrt[n]{\left(i^t \right)^n} $と変形できますが、これは$ i^t $と等しいとは限りません。なぜなら、$ i^{nt} $には「原点を何周したか」の情報が含まれておらず、常に$ -\pi < \arg{\left(i^{nt}\right)} \leq \pi $として扱われ、この偏角が$ \frac{1}{n} $倍になるからです。
この様子を、図にしてみましょう。

$ y = \arg{\left(\sqrt[n]{i^{nt}}\right)} $ ($ n = 7 $のとき)

$ i^4 = 1 $なので、$ t = 4 $が$ 1 $周に対応することに注意してください。

元の式に戻ると、分母にあるのは$ \sqrt[n]{i^{nt}}.\operatorname{real} $、すなわち$ \sqrt[n]{i^{nt}} $の実部です。ということは、$ \arg $は絶対値を取っても結果は変わらないですね。すると、

$ y = \left|\arg{\left(\sqrt[n]{i^{nt}}\right)}\right| $ ($ n = 7 $のとき)

見たことのある形が現れました。$ 1 $周すなわち$ 0 \leq t < 4 $の間で$ 7 $回線が上下することから、ID21とやっていることが本質的に同じであることがわかりますね。

この実部を取るということは、$ \cos $を外側に付けるということなので、これを分母に置くことでID21と同様の式が得られます。ちなみに、ID21の式にあった分母の$ n $は$ n $乗根として表現されています。

ID23: 三葉結び目

式: $ \left(\cos t+2\cos2t,\sin t-2\sin2t\right) $
難易度: ★★★☆☆

まずこのグラフが$ 3 $回対称であることを示します。そのために、複素数を使用します。

$ \alpha = e^{it} $とおくと、$ z(t) = \alpha + 2\alpha^{-2} $です。$ |\alpha| = 1, |2\alpha^{-2}| = 2 $なので、$ z(t) $は原点の周りを$ 2 $周します。
また、$ |z(t)|^2 $は次のように計算できます:

\begin{align*} |z(t)|^2 &= \left(\alpha + 2\alpha^{-2}\right)\left(\alpha^{-1} + 2\alpha^2\right) \\ &= 1 + 2\alpha^3 + 2\alpha^{-3}+4 \\ &= 5 + 2\left(\alpha^3 + \alpha^{-3} \right) \\ &= 5 + 4 \cos{3t} \end{align*}

よって、$ |z(t)| $は$ 1 $周の間に$ 3 $周期分値が増減することが分かります。

これをもとにグラフの概形を描くと、Grapharyにあるような形が得られます。

ID24: 欠番

ID24は欠番のようです。もともと現在のID39が入っていたようです。

ID25: 典型的な5つの5つの花弁を持つ花

式: $ r=\sin5\theta+\left|\cos5\theta\right|+1 $
難易度: ★★☆☆☆

また$ 5 \theta $が出てくる式です。

$ \left|\cos5\theta\right| $が微分不可能になるのは$ 5\theta = \left(n + \frac{1}{2}\right) \pi $($ n $は整数)なので、このタイミングでグラフが尖ります。
また、$ 5\theta = \frac{1}{2}\pi $のとき$ \sin{5\theta} $は極大値$ 1 $、$ 5\theta = \frac{3}{2}\pi $のとき$ \sin{5\theta} $は極小値$ -1 $を取るので、グラフのへこみに対応します。
とくに、$ 5\theta = \frac{3}{2}\pi $のとき$ r = -1 + 0 + 1 = 0 $なので、グラフは原点を通ります。

ID26: おしべ付きの切れ込みあり花

式: $ r=1+2\left|\cos5\theta\right|+3\sin5\theta $
難易度: ★★★☆☆

ID25とほぼ同じですが、$ r < 0 $になることがあるため、花弁の間の隙間の反対側に切れ込みが入ったように見えます。

ID27: キキョウの花

式: $ r=1+\sqrt{\left|\sin\frac{5}{2}\theta\right|}-\frac{\left|\sin5\theta\right|}{3} $
難易度: ★★★☆☆

ID19の符号を$ 1 $箇所変えただけですが、見た目は大きく異なります。$ \varphi = 5 \theta $とおくと、式の各部分のグラフは次のようになります。

赤:$ \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} $ 緑:$ -\frac{|\sin\varphi|}{3} $ 青: $ r \left(= 1 + \sqrt{\left|\sin{\frac{\varphi}{2}}\right|} - \frac{|\sin\varphi|}{3}\right) $

$ \varphi = 0, 2\pi $ではグラフが$ y $軸に平行な直線に近づく一方、$ \varphi = \pi $ではグラフが$ 0 $でない角度で折れ曲がっているのが特徴です。実際のID27のグラフでも、よく見たら内側と外側で尖り方が違っています。

ID28: てきちょくのふきだし

式: $ \left|x-y\right|+\left|\left|x+y+\left|x\right|\right|-x\right|=1 $
難易度: ★★★★☆

Grapharyの作成者である【彳▼亍 ▼てきちょく】さんが使っている吹き出しのアイコンです。
絶対値記号が$ 4 $組もあって解析が難しそうに見えますが、場合分けは意外と単純にできます。

とくに、場合分けごとに考えると絶対値が外れて$ x $と$ y $の$ 1 $次式になるため、各領域では線分、半直線、または直線となることがわかります。

各領域の境界線は、次のようになります。

これらを図示すると、こうなります。

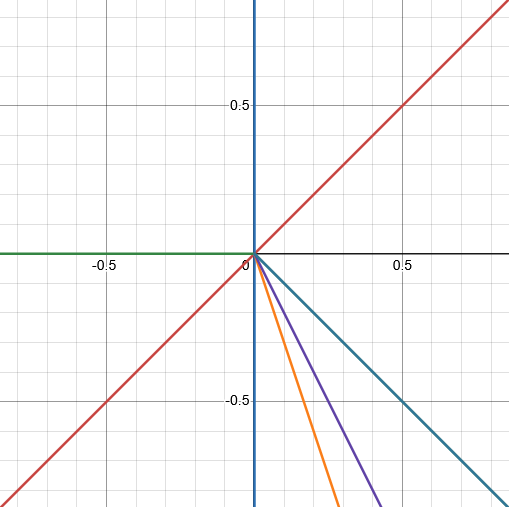全ての境界線

あとは、各領域(境界線上でもよい)に含まれる少なくとも$ 2 $点を見つければ、それらを線で結ぶことで最終的な図形が得られます。境界線上の点が見つかれば、それは境界の両側の線分に共通して存在する点なので必要な点の個数を減らせます。

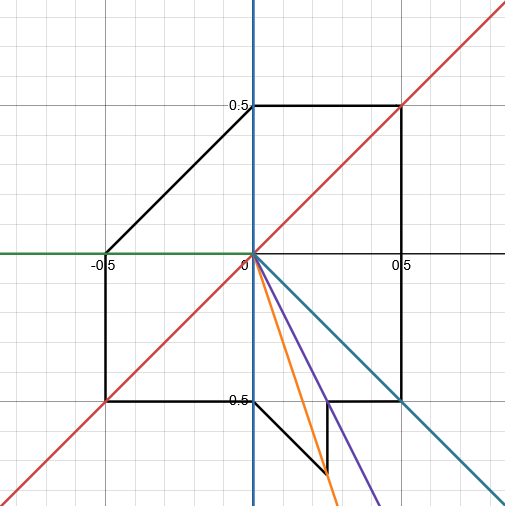最終的に得られる図形

ID30: 円で挟まれた領域

式: $ \left|x^{2}+y^{2}-2\right|<1 $
難易度: ★☆☆☆☆

絶対値を外すと$ 1 < x^2 + y^2 < 3 $になるので、円環状の領域(アニュラス)になります。不等号にイコールが付いていないので境界は含みません。