Grapharyに収録されているグラフを解説する(ID1～10)

この記事では、【彳▼亍 ▼てきちょく】さんの Graphary を題材に、「なぜその式からその形が得られるか」を解説します。

収録数が多いので、10個ごとに記事を区切って解説します。今回はID1～ID10を解説します。

基本的にグラフはこの記事に載せないので、Grapharyもご参照ください。

相互リンク

• ID1～10 ←いまここ
• ID11～20
• ID21～30
• ID31～41

一覧

ID1: 円

式: $ \left(\cos t,\sin t\right) $
難易度: ☆☆☆☆☆

もはや説明するまでもありません。むしろ、「こうすると円が描ける」ではなく、「こうなるように$ \cos $と$ \sin $が定義されている」と言った方が正しいです。

ID2: 楕円ほど細長くないが丸みを帯びた円

式: $ \left(\cos\left(t-\frac{\sin2t}{2}\right),2\left|\sin t\right|\sin t\right) $
難易度: ★★★★★

三角関数の中に三角関数が入っています。難しいので、$ x $座標と$ y $座標に分けて考えましょう。

$ x $座標

$ \frac{d}{dt}\frac{\sin{2t}}{2} = \cos{2t} $なので、$ x $座標の$ \cos $の中身は狭義単調増加です。
また、$ \sin{x} = x - \frac{x^3}{6} + \cdots $と展開できるので、$ t-\frac{\sin2t}{2} \approx \frac{2}{3}t^3 $と近似できます。とくに、$ t = 0 $での$ 2 $階までの微分係数は$ 0 $になるので、$ t $に対して$ x $座標が減少するのが遅くなります。
さらに、$ \cos{x} = 1 - \frac{x^2}{2} + \cdots $と展開できることに注意すると、$ \cos\left(t-\frac{\sin2t}{2}\right) $は$ t \approx 0 $のときに$ O\left( t^6 \right) $の速さで減少することが分かります。
一方、$ \sin{2t} $は$ t $が$ \frac{\pi}{2} $の整数倍のときには$ 0 $になるので、それまでに「追いつく」必要があるために。

$ y = \cos\left(x-\frac{\sin2x}{2}\right) $のグラフ

$ y $座標

$ 2\operatorname{sgn}(\sin{t}) \cdot \left| \sin^2{t} \right| $と書くことができます。$ t = 0 $では$ 2 $回までの微分係数が$ 0 $になります。

$ y = 2\left|\sin x\right|\sin x $のグラフ

$ x $座標と$ y $座標をまとめる

$ x $座標も$ y $座標も増加・減少の様子はそれぞれ$ \cos, \sin $と変わらないので、大まかには楕円と似た形であることが分かります。
一方、$ t \approx 0$のとき$ x $座標が$ 1 - O\left(t^6\right) $であるのに対し、$ y $座標は$ O\left(t^2\right) $なので、$ x - 1 = -O\left(y^3\right) $となります。係数を計算すると、$ x - 1 \approx -\frac{1}{36}y^3 $となります。実際、グラフを比較してみると、

黒:ID2のグラフ 紫:$ x - 1 = -\frac{1}{36}y^3 $

このように、$ -0.6 < y < 0.8 $くらいの範囲で目視では区別がつかないことが分かります。

また、楕円の場合は$ x - 1 = O\left(y^2\right) $のような形になるので、オーダーの議論からもこのグラフが楕円より外側に膨らんでいることが分かります。

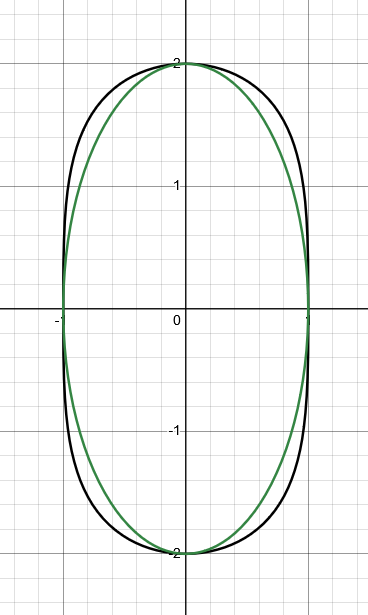黒:ID2のグラフ 緑:楕円

ID3: 1と0を繰り返す線

式: $ y = \operatorname{mod}\left(\operatorname{floor}\left(x-1\right),2\right) $
難易度: ★☆☆☆☆

式の中に$ \operatorname{mod} $と$ \operatorname{floor} $という見慣れない関数が出てきましたが、$ \operatorname{mod} $は「余り」、$ \operatorname{floor} $はガウス記号のことです。厳密な定義を書くと、こうなります。

これらの定義に従って、$ x - 1 = 2y + a + b $($ y $は整数、$ a $は$ 0 $または$ 1 $、$ z $は$ 0 \leq z < 1 $を満たす実数)とおいて式を変形すると、グラフの形は容易にわかります。

ID5: 対角線が2のひし形

式: $ \left|x\right|+\left|y\right|=1 $
難易度: ★☆☆☆☆

構成の都合上ID4よりID5を先に解説します。

式の形から$ x $軸と$ y $軸に関して対象であることが分かります。第1象限について考えるとこれは線分なので、あとはこの線分を折り返すことでひし形が完成します。
実際には正方形になりますが、正方形はひし形なのでひし形と言っても間違いではありません。

ID4: 1辺が1の正方形

式: $ \left|x+y\right|+\left|x-y\right|=1 $
難易度: ★★☆☆☆

$ X = x + y, Y = x - y $とおくことでこの式は1つ前の式と全く同じ形になります。

あとは$ X, Y $を$ x, y $に戻すだけですが、これは$ XY $平面上のグラフに

• $ Y = X $で反転させる
• 原点を中心に時計回りに$ \frac{\pi}{4} $回転させる
• 原点を中心に$ \frac{1}{\sqrt{2}} $倍に縮小する

の3つの操作を順に行ったときに得られます。

これは複素数を考えると直ちにわかり、
$ (x + yi)(1 + i) = (x - y) + (x + y)i = Y + Xi $
であることから従います。

ID6: 繋がった円

式: $ \left(\operatorname{mod}\left(x+1,2\right)-1\right)^{2}+y^{2}-1=0 $
難易度: ★★☆☆☆

整数$ a $ごとに、$ 2a - 1 \leq x \leq 2a + 1 $の範囲で考えると、この式は$ \left(x - 2a\right)^{2}+y^{2}=1^{2} $と変形でき、それぞれの$ a $で$ 1 $つの円を描くことがわかります。

ID7: ジグザグな線

式: $ y = \arcsin\left(\sin\left(x\right)\right) $
難易度: ★★☆☆☆

$ \arcsin $の値域が$ -\frac{\pi}{2} $以上$ \frac{\pi}{2} $以下であることに注意すると、実数$ a $に対する$ \arcsin\left(\sin\left(a\right)\right) $は次のように作図できます。

$ \arcsin\left(\sin\left(a\right)\right) $の作図

1. $ y = \sin{x} $のグラフを用意し、$ P(a, \sin{a}) $をとる。
2. $ P $を通り$ x $軸に平行な直線と、$ y = \sin{x} $の$ -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} $の部分との共有点がちょうど$ 1 $個存在するので、それを$ Q $とする。
3. $ Q $を通り$ y $軸に平行な直線と$ x $軸との交点を$ R $とする。
4. $ R $の$ x $座標が$ \arcsin\left(\sin\left(a\right)\right) $である。

このような作図をすると、ギザギザが出てくることは明らかですね。

ID10: ジグザグな線

式: $ y = \arccos\left(\cos\left(x\right)\right) $
難易度: ★★☆☆☆

$ \arccos\left(\cos\left(a\right)\right) $の作図

番号が前後しますが、関連性があるので隣同士に並べました。$ \arcsin\left(\sin\left(x\right)\right) $と同じように作図を考えることで、Grapharyにある線が描けることが分かります。

ID8, 9: ジグザグな線

(ID8)
式: $ y = \arcsin\left(\cos\left(x\right)\right) $
難易度: ★★☆☆☆

(ID9)
式: $ y = \arccos\left(\sin\left(x\right)\right) $
難易度: ★★☆☆☆

$ \cos{x} = \sin{\left( x + \frac{\pi}{2} \right)}, \sin{x} = \cos{\left( x - \frac{\pi}{2} \right)} $から即座に従います。