【超局所層理論第2回】層の演算に対するマイクロ台のふるまい
はじめに
こんにちは！超局所層理論の第2回です．今回はマイクロ台が様々な層の操作によってどのようにふるまうかを調べていきたいと思います．今回も証明はほとんどしないでお気持ちだけ説明します．
前回の復習
$\bfk$を有限な大域次元を持つ環，$X$を多様体とします． 前回 は$X$上の$\bfk$加群の層の複体$F \in \Db(\bfk_X)$に対して，そのコホモロジーが伝播しない余方向として層のマイクロ台$\MS(F)$という$X$の余接束$T^*X$の錐状閉集合を定義したのでした．マイクロ台に入っているかどうかは相対コホモロジーの茎$\RG_{\{ \varphi \ge \varphi(x_0) \}}(F)_{x_0}$によって決まっているのでした．そして様々な層についてそのマイクロ台がどうなっているのか見ました．また良い状況ではマイクロ台が層の形を強く制限することがあることも見ました．
層の演算とマイクロ台
層にはGrothendieckの六演算をはじめとする様々な演算があったのでした．これらの演算に対して層のマイクロ台がどのようにふるまうのか，特に操作を施した後のマイクロ台を元のマイクロ台で評価する方法について考えます．
順像と逆像のマイクロ台
多様体の射$f \colon X \to Y$による順像・逆像のマイクロ台について考えます．射$f$は次の可換図式を誘導します：
\begin{xy}
\xymatrix{
T^*X \ar[rd]_-{\pi_X} & X \times_Y T^*Y \ar[l]_-{f_d} \ar[r]^-{f_\pi} \ar[d] & T^*Y \ar[d]^-{\pi_Y} \\
& X \ar[r]_-{f} & Y.
}
\end{xy}
ここで，右の四角は引き戻しの図式（よって$f_\pi \colon X \times_Y T^*Y \to T^*Y$は標準的な射影）で$f_d \colon X \times_Y T^*Y \to T^*X$は微分写像$T_x f \colon T_xX \to T_{f(x)}Y$の転置から誘導される射です．
Sheaves on Manifoldsでは上の射$f_d$は${}^t f'$という記号で書かれていた．別の文献では$f_d$を$\rho_f$，$f_\pi$を$\varpi_f$と書くこともあるので注意せよ．
さて上の記号の準備の下で，まず順像のマイクロ台について考えます．
$F \in \Db(\bfk_X)$として，$f$が$\Supp(F)$上固有であると仮定する．このとき，
$$
\MS(Rf_*F) \subset f_\pi f_d^{-1}(\MS(F))
$$
が成立する．さらに$f$が閉埋め込みの場合は等式が成立する．
$y_0 \in Y$として$\psi \colon Y \to \bbR$を$\psi(y_0)=0$となる$C^\infty$級函数とすると，同形
\begin{align}
\RG_{\{\psi \ge 0 \}}(Rf_*F)_{y_0}
& \simeq
(Rf_* \RG_{\{\psi \circ f \ge 0 \}}(F))_{y_0} \\
& \simeq
\RG(f^{-1}(y_0);\RG_{\{\psi \circ f \ge 0 \}}(F)|_{f^{-1}(y_0)})
\end{align}
が得られる．ここで二つ目の同形に固有であることを用いた．よって包含が成立することが分かる．閉埋め込みの場合はゼロ拡張なのでもう少し頑張ればよい．
次に逆像について考えましょう．まずは沈めこみの場合を述べたいのですが，その前に前に本質的な例を見てみます．
$q_1 \colon \bbR^2 \to \bbR$を第一射影とする．このとき，$G \in \Db(\bfk_\bbR)$に対して
$$
\MS(q_1^{-1}G) \subset \{ (x,y;\xi,0) \mid (x,y) \in \bbR^2, \xi \in \bbR \}
$$
が成り立つ．$q_1^{-1}G$は第2成分の方向には同じものを並べているので，この方向に動かしても層は変化しないからである．
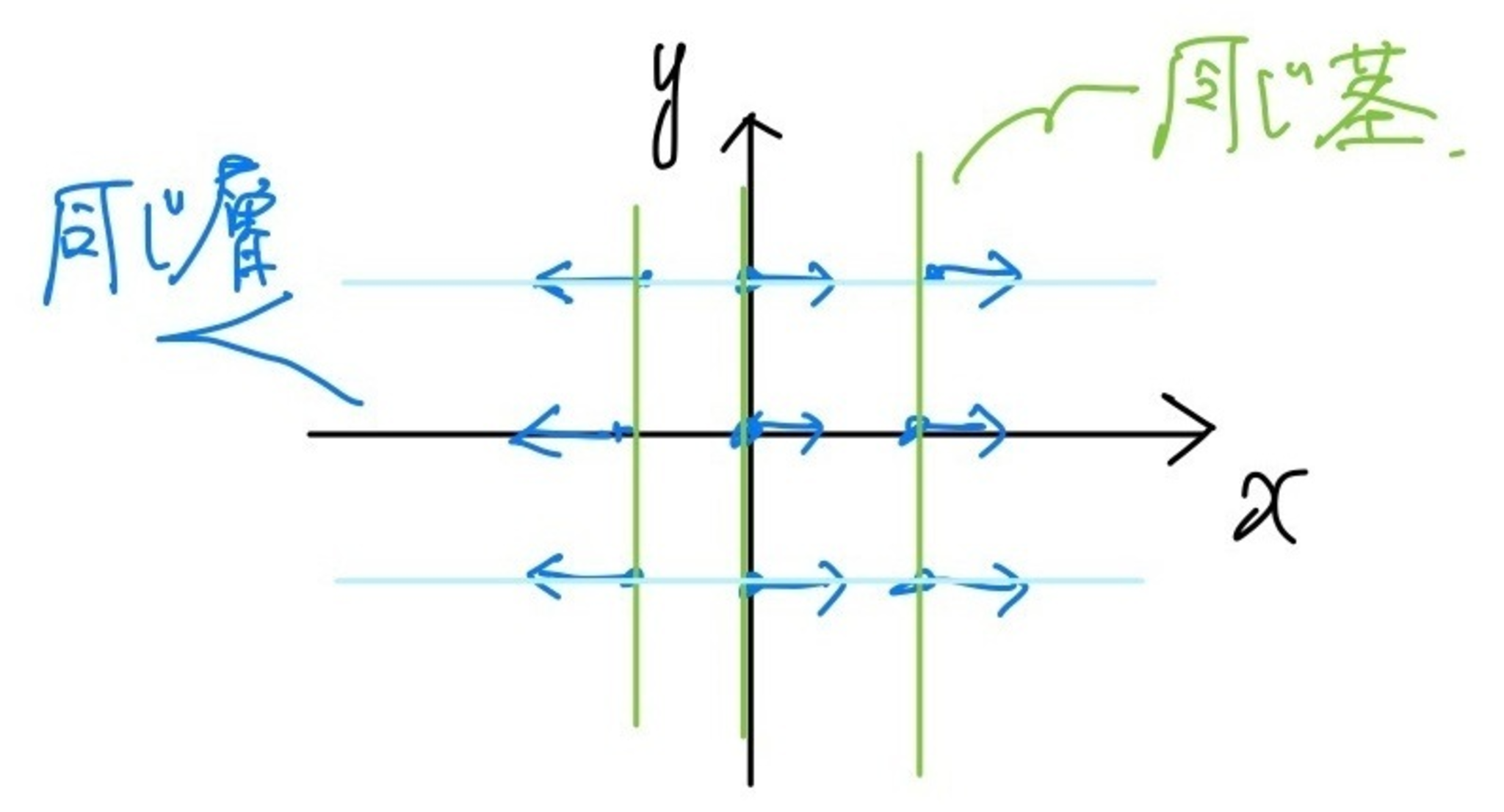第1射影による引き戻しのマイクロ台
大事なことは，ある意味でこの逆が成立することである．すなわち，$F \in \Db(\bfk_{\bbR^2})$が
$$
\MS(F)) \subset \{ (x,y;\xi,0) \mid (x,y) \in \bbR^2, \xi \in \bbR \}
$$
を満たせば，ある$G \in \Db(\bfk_\bbR)$が存在して$F \simeq q_1^{-1}G$を満たす．これもマイクロ台が層の形を制限するタイプの主張である．
上の例は次のように沈めこみに一般化できます．$f \colon X \to Y$が沈めこみの場合は$f_d \colon X \times_Y T^*Y \to T^*X$は単射であることに注意します．主張は沈めこみによる逆像はマイクロ台の定義に出てくる相対コホモロジーの茎が計算できることから示すことができますが詳細は省略します．
$f \colon X \to Y$が沈めこみであると仮定する．
(i) $G \in \Db(\bfk_Y)$に対して，
$$
\MS(f^{-1}G) = f_d f_\pi^{-1}(\MS(G))
$$
が成り立つ．
(ii) $F \in \Db(\bfk_X)$に対して次の3条件は同値である．
(1) $f$のファイバー上で$F$は局所定数層である．
(2) $X$上局所的に$G \in \Db(\bfk_Y)$が存在して$F \simeq f^{-1}G$が成り立つ．
(3) $\MS(F) \subset f_d(X \times_Y T^*Y)$が成り立つ．
(ii)もやはりマイクロ台が層の形を制限するというタイプの主張であることにも注目しましょう．
次に一般の射$f \colon X \to Y$に対する逆像を考えます．評価の主張を述べるためには次の非特性的という概念が必要になります．
$A$を$T^*Y$の錐状閉部分集合とする．このとき，$f \colon X \to Y$が$A$に対して非特性的であるとは
$$
f_\pi^{-1}(A) \cap f_d^{-1}(0_X) \subset X \times_Y 0_Y
$$
を満たすことをいう．$G \in \Db(\bfk_Y)$のとき，$f$が$G$に対して非特性的であるとは$\MS(G)$に対して非特性的であることをいう．$f$が埋め込みであるときは$X$が非特性的ともいう．
$f$が沈めこみならば$f_d^{-1}(0_X)=X \times_Y 0_Y$なので，$T^*Y$の任意の錐状閉部分集合$A$に対して非特性的であることに注意しましょう．$f$が$A$に対して非特性的ならば$f_d f_\pi^{-1}(A)$は$T^*X$の錐状閉部分集合であることが示せます．
次が射がマイクロ台に対して非特性的な場合の逆像の性質です．上付きびっくりの性質（ 層理論第8回 ）で見たように，$G \in \Db(\bfk_Y)$に対して標準的な射$f^{-1}G \otimes \omega_f \to f^!G$があることを思い出しましょう．
$G \in \Db(\bfk_Y)$として，$f$が$G$に対して非特性的であると仮定する．このとき，
(i) $\MS(f^{-1}G) \subset f_d f_\pi^{-1}(\MS(G))$が成り立つ．
(ii) 自然な射$G \in \Db(\bfk_Y)$に対して標準的な射$f^{-1}G \otimes \omega_f \to f^!G$は同形である．
$f$をグラフへの埋め込みと射影$X \xrightarrow{g} X \times Y \xrightarrow{h} Y, g(x)=(x,f(x))$に分解する．よく考えると，$f_d, f_\pi$と$g_d, g_\pi, h_d, h_\pi$に付随したファイバー積の図式があるので，$g$と$h$についてそれぞれ示せば十分である．$h$については命題2で示した．閉部分多様体の埋め込みの場合は，順像のマイクロ台の評価（命題1）を用いて頑張ることで示せる．
上の(ii)が 層理論第8回 で予告していた「上付きびっくりと逆像が（相対向き付け層の差を除いて）同形になる条件を層に応じて述べたもの」なのです．沈めこみは任意の層に対して非特性的なので以前見た主張はこの特殊な場合と思うこともできます．このようにして基本的な同形が成り立つ条件を述べる際にもマイクロ台の概念が必要なのです．
テンソル積とsheaf Homのマイクロ台
次にテンソル積とsheaf Homのマイクロ台について考えます．そのために外テンソル積と直積上のsheaf Homのマイクロ台はどうなるかを述べておきましょう．ここで余接束$T^*X$の錐状閉部分集合$A$に対して，$-A \subset T^*X$で対蹠写像$T^*X \to T^*X, (x;\xi) \mapsto (x;-\xi)$による$A$の像をあらわします．証明は$X$と$Y$の側で別々に分解されていることからできますが詳細は省略します．
$X,Y$を多様体，$q_X \colon X \times Y \to X, q_Y \colon X \times Y \to Y$をそれぞれ射影とし，$F \in \Db(\bfk_X), G \in \Db(\bfk_Y)$とする．
(i) $\MS(q_X^{-1}F \lten q_Y^{-1}G) \subset \MS(F) \times \MS(G)$.
(ii) $\MS(\cRHom_{X \times Y}(q_Y^{-1}G, q_X^!F)) \subset \MS(F) \times (-\MS(G))$.
さて上の直積上の評価に基づいてテンソル積とsheaf Homのマイクロ台の評価を与えましょう．余接束$T^*X$の二つの錐状閉部分集合$A, B$に対して，$T^*X$の部分集合$A+B$を
$$
A+B := \{ (x;a+b) \mid x \in \pi(A) \cap \pi(B), a \in A \cap \pi^{-1}(x), b \in B \cap \pi^{-1}(x) \}
$$
により定めます．もし$A \cap (-B) \subset 0_X$ならば，$A+B$も$T^*X$の錐状閉部分集合となることがチェックできます．
$F,G \in \Db(\bfk_X)$とする．
(i) $\MS(F) \cap (-\MS(G)) \subset 0_X$ならば，$\MS(F \lten G) \subset \MS(F)+\MS(G)$が成り立つ．
(ii) $\MS(F) \cap \MS(G) \subset 0_X$ならば，$\MS(\cRHom(F,G)) \subset (-\MS(F))+\MS(G)$が成り立つ．
$\delta \colon X \to X \times X, x \mapsto (x,x)$を対角射とする．すると，
\begin{align}
F \lten G
& \simeq
\delta^{-1}(q_1^{-1}F \lten q_2^{-1}G), \\
\cRHom(F,G)
& \simeq
\delta^! \cRHom(q_2^{-1}F,q_1^!G)
\end{align}
が成り立つ．ゆえに逆像のマイクロ台の評価（命題3）と上の命題4から結果が従う．
以上が基本的な層の演算に対するマイクロ台のふるまいです．しかしながら，上で見た主張たちには非特性的という条件に由来する仮定がついていました．一般の状況で逆像・テンソル積・sheaf Homのマイクロ台を知りたい場合もあり，そのときは$f_d, f_\pi$やファイバーごとの和$+$だけではない，もっと高度な余接束の部分集合に対する操作を考える必要があります．ここでは詳細は述べませんが，以降ではそれを使うことがあります（そのうち元気があれば書くかも）．なんにせよ大事なことは，層から基本演算の組合せで新しい層を作れば，その層のマイクロ台を評価することができるということです．またここでは説明しませんでしたが， 層理論第6回 で見た層の合成演算（積分変換）についても，非特性的な条件下でマイクロ台を評価することができることにも注意しておきましょう．
超局所切り落とし
上で層の演算を施した後のマイクロ台の評価を見てきました．これらに基づいて「マイクロ台を切り落とす」ことができないかということを考えます．すなわち，有限次元実ベクトル空間$E$と$E$の閉凸錐$\gamma$に対して，$X \times E$上の層に対する演算でマイクロ台が$T^*X \times E \times \gamma^\circ$に入るようになるものを作ることを考えます．ここで$\gamma^\circ := \{ \xi \in E^* \mid \langle \xi,v \rangle \ge 0 \ (v \in \gamma) \}$は双対錐でした．もしこれができれば層$F$に対して，閉部分集合$Z$への台の切り落とし$F_Z$が出来たように，余接束の中でマイクロ台の切り落としができることになります．このアナロジーで考えると切り落としの操作は$T^*X \times E \times \gamma^\circ$の中ではなるべく層を変更しないようにもなっていてほしいわけです．
上で述べたマイクロ台の切り落としは次のように実現することができます．$\tilde{q}_i \colon X \times E \times E \to M \times E \ (i=1,2)$を$E \times E$を第$i$成分に射影する射，$s \colon X \times E \times E \to X \times E, (x,v_1,v_2) \mapsto (x,v_1,v_2)$を$E$における加法による射とします．ここで$\bfk_\gamma \in \Db(\bfk_E)$のマイクロ台は$\MS(\bfk_\gamma) \subset E \times \gamma^\circ$であったことを思い出しましょう（
第1回
の例3）．すると，逆像・順像・テンソル積のマイクロ台の評価を用いると$F \in \Db(\bfk_{X \times E})$に対して
$$
Rs_*(\tilde{q}_1^{-1}F \lten \bfk_{X \times E \times \gamma} )
\subset T^*X \times E \times \gamma^\circ
$$
となることがチェックできます．ここで，順像は台の上で固有とは限らないので命題1をそのまま使うことはできないのですが，$s$が線形写像であることを使うと評価ができます．そこで$P_\gamma(F):=Rs_*(\tilde{q}_1^{-1}F \lten \bfk_{X \times E \times \gamma} ) \in \Db(\bfk_{X \times E})$と置きましょう．実はこの操作はマイクロ台の切り落としができるのみでなく，またしても「層のマイクロ台がこの錐状集合$T^*X \times E \times \gamma^\circ$に入っていればこの形に書ける」というタイプの命題が成り立ちます．任意の$E$の閉凸錐$\gamma$に対して$\bfk_{X \times E \times \gamma} \to \bfk_{X \times E \times \{0\}}$という標準的な射が存在して，しかも$Rs_*(\tilde{q}_1^{-1}F \lten \bfk_{X \times E \times \{0\}} ) \simeq F$が成り立つことに注意します．したがって，任意の$F \in \Db(\bfk_{X \times E})$に対して，標準的な射
$$
P_\gamma(F) \to F
$$
が存在します．
$F \in \Db(\bfk_{X \times E})$とする．
(i) $\MS(F) \subset T^*X \times E \times \gamma^\circ$であることと標準的な射$P_\gamma(F) \to F$が同形であることは同値である．
(ii) 完全三角$P_\gamma(F) \to F \to F' \to P_\gamma(F)[1]$であって$\MS(F') \cap (T^*X \times E \times \Int(\gamma^\circ))=\emptyset$となるものが存在する．ここで$\Int(A)$は$A$の内部をあらわす．
上の定理はSheaves on Manifoldsでは$\gamma$位相を用いて主張が述べられていたが，ここでは近年のシンプレクティック幾何学への応用で発展した層の畳み込みを用いた主張に書き直した．これは例えばGuillermou-Schapiraで見つけられる．
(ii)は$T^*X \times E \times \Int(\gamma^\circ)$だけで見て，それ以外のところのマイクロ台を無視してやれば標準的な射$P_\gamma(F) \to F$が同形のように思えるということを述べています．このように余接束$T^*X$の中である部分だけに着目して局所的に見ることを超局所的な考え方というのでした．こうして段々と超局所的な見方が現れてきたと思います．(ii)の証明は完全三角$\bfk_{\gamma \setminus \{0\}} \to \bfk_\gamma \to \bfk_{\{0\}} \to \bfk_{\gamma \setminus \{0\}}[1]$を考えて$\MS(\bfk_{\gamma \setminus \{0\}}) \subset E \times (E^* \setminus \Int(\gamma^\circ))$であることを使えば得られます．定理より$P_\gamma(F)$は余接束$T^*X$内でマイクロ台をうまく切り落としているため超局所切り落としと呼ばれています．函手$P_\gamma \colon \Db(\bfk_{X \times E}) \to \Db(\bfk_{X \times E})$は$P_\gamma \circ P_\gamma=P_\gamma$を満たし射影子となります．この射影子は近年（2021年現在）特にシンプレクティック幾何学との関係で有効に用いられています．
まとめ
今回は
- 様々な層の演算に対するマイクロ台のふるまい
- マイクロ台を閉凸錐状集合に切り落とす超局所切り落とし
について説明しました．次回は余接束の中で局所的に見る・ある部分の外のマイクロ台は無視するという考え方を推し進めて圏論的超局所化を導入したいと思います．それではまた！
