【超局所層理論第1回】層のマイクロ台の定義と例
はじめに
こんにちは！今回から超局所層理論について説明していきます．超局所層理論は柏原とSchapiraによって創始された理論で，層を方向も含めて解析する枠組みを提供します．これは様々な分野のいろいろな定理の統一的な理解はもちろん，解析学や幾何学における多くの応用も与えます．この理論について筆者が説明できる部分をゆっくり時間をかけて説明していきたいと思います．全般的に証明はあまりせずに気持ちだけを伝えるため，実際の証明ではあとで説明することを使うこともあり得ることを注意しておきます．
層とその導来圏のおさらい
$X$を位相空間，$\bfk$を有限な大域次元を持つ可換環とします．このとき，$X$上の$\bfk$加群の層の圏$\Mod(\bfk_X)$はアーベル圏になるのでした（ 層理論第2回 ）．ここから，層の導来圏$\D^*(\bfk_X):=\D^*(\Mod(\bfk_X))$を考えることができ，そこにはGrothendieckの六演算が定まって随伴の関係を満たすのでした（ 層理論第6回 ・ 第7回 ）．多様体だけを考えると六演算は有界導来圏$\Db(\bfk_X)$たちの間の函手に落ちるのでした（ 層理論第8回 ）．
さて，今回たくさん出てくる台の切り落としと相対コホモロジーについてもうちょっとだけ思い出しておきましょう．詳しくは
層理論第5回
・
第6回
を参照してください．$i \colon Z \hookrightarrow X$を$X$の局所閉部分集合の埋め込みとします．このとき，層$F \in \Dp(\bfk)$に対して
$$
F_Z := i_!i^{-1}F \ \in \Dp(\bfk_X)
$$
と定めたのでした．特に$F$が定数層$M_X \ (M \in \Dp(\bfk))$のときは$M_Z:=(M_X)_Z$と書いてしまうのでした．また，$Z$に台を持つ層を対応させる函手$\Gamma_Z$の右導来函手として$\RG_Z \colon \Dp(\bfk_X) \to \Dp(\bfk_X)$を定めると，同形$\RG(F) \simeq \cRHom(\bfk_Z,F)$が成り立つのでした．この相対コホモロジーで大事な完全三角は，$Z$が閉集合のときに$j \colon U:=X \setminus Z \hookrightarrow X$を開埋め込みとしてとして
$$
\RG_Z(F) \to F \to Rj_*j^{-1}F \to \RG_Z(F)[1]
$$
なるものでした．大域切断を取れば
$$
\RG_Z(X;F) \to \RG(X;F) \to \RG(U;F|_U) \to \RG_Z(X;F)[1]
$$
となるので，対象$\RG_Z(X;F)$を使って射$\RG(X;F) \to \RG(U;F|_U)$の同形が判定できるのでした．ひとつ前の完全三角はこれを層のまま扱っているので，層$\RG_Z(F)$は$F$の$U$への制限がどうなっているかを局所的にあらわすものだと思えます．
層のマイクロ台の定義
超局所層理論は何かというといろいろな答えがありうると思うのですが，一つの捉え方は「層に対するモース理論」（のようなもの）というものです．モース理論は多様体上のモース函数$\varphi \colon X \to \bbR$があったときに，その劣位集合$\{\varphi < c\}=\{x \in X \mid \varphi(x)< c \}$のトポロジーが$c \in \bbR$によってどのように変化するかを知ることができるものでした．そこでは$c$が$\varphi$の臨界値を越えるときのみにトポロジーの変化が起こるのでした．特に，モース理論によって$\bfk$係数のコホモロジー$H^n(\{\varphi < c\};\bfk)$の変化も知ることができます．ここで係数を定数層$\bfk_X$から一般の層（正確には層の導来圏の対象）$F \in \Db(\bfk)$に取り換えて，$F$係数の劣位集合のコホモロジー$H^n(\{\varphi < c\};F)$については何が分かるだろうか？という問いが考えられます．このとき，$c$がどんな値を越えるときにコホモロジーが変化しうるでしょうか？これを記述するのが層のマイクロ台というものなのです．
さてマイクロ台を定義するために，以下ずっと，おそらく超局所層理論の連載記事の最後まで$X$を境界のない$C^\infty$級多様体とします．このとき，$\pi \colon T^*X \to X$で$X$の余接束をあらわし，その局所斉次座標を$(x;\xi)$であらわします．「超局所 (microlocal)」という言葉は「余接束内で局所」という意味で佐藤幹夫一派が使いだしたと言われています．つまり超局所とは考えている多様体$X$内で局所的に考えるのみならず，その（余）方向である余接束も考えて解析することを言います．層$F \in \Db(\bfk_X)$のマイクロ台$\MS(F)$は余接束$T^*X$内の部分集合として定義されます．正確な定義を与える前に，マイクロ台の気持ちを説明しておきましょう．$X=\bbR$のとき，余接束の点$p=(x_0;\xi_0) \in T^*X$がマイクロ台に入っていない，つまり$p \not\in \MS(F)$であるとは$p$の方向にすべてのコホモロジー類が少しは一意に拡張できることをいいます．もっと正確に言うと，$p$が定める半空間$\Omega=\{x \in X \mid \langle \xi_0, x-x_0 \rangle <0 \}$上の任意のコホモロジー類が$x_0$を中心とした十分小さい球$B$を付け加えた空間に一意的に拡張できる，すなわち任意の$n \in \bbZ$に対して，制限写像
$$
\varinjlim_{x_0 \in B} H^n(\Omega \cup B;F) \to H^n(\Omega;F)
$$
が同形になることをいいます（図1参照）．
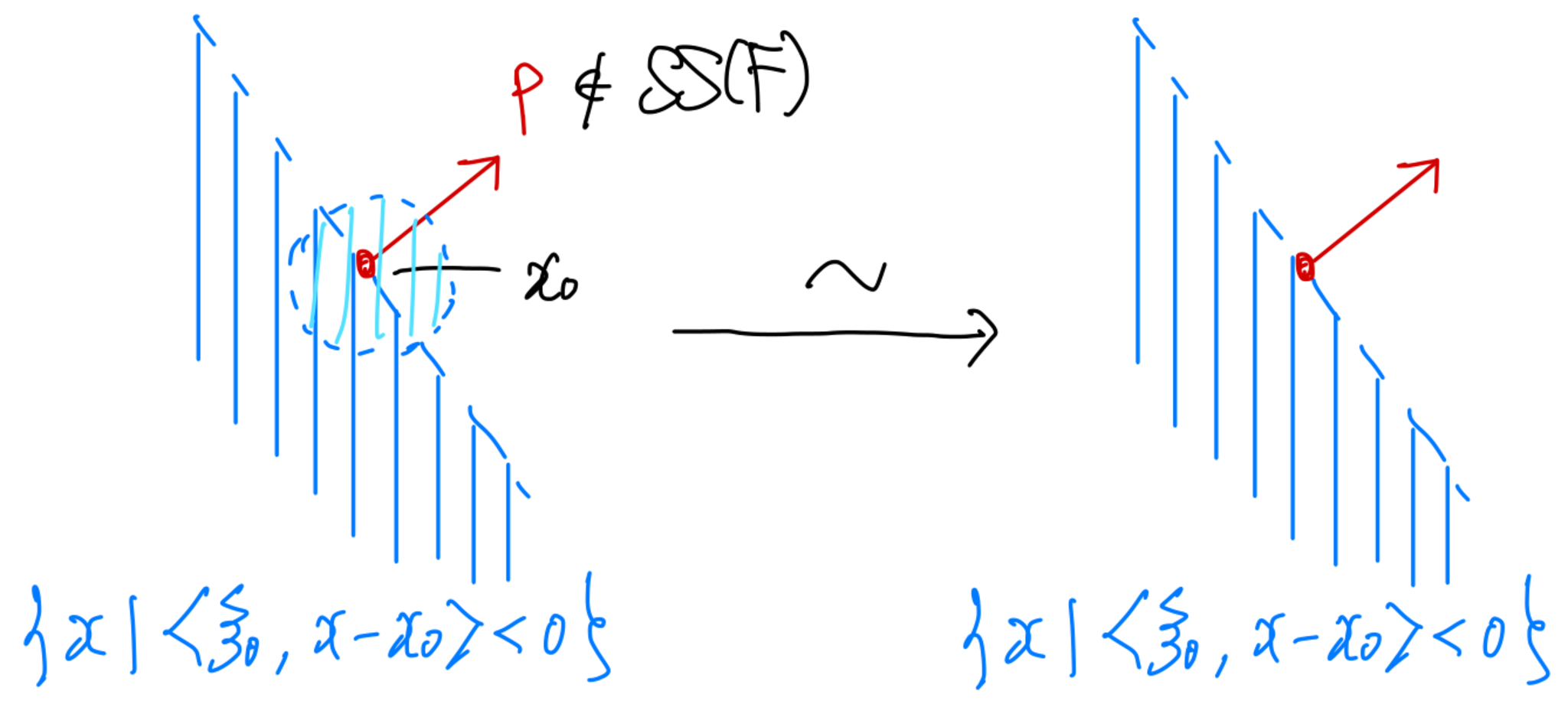マイクロ台の気持ち
気持ちとしては$p$の方向に"解析接続できる"といった感じでしょうか（実際マイクロ台の定義は微分方程式の解の解析接続がもともとの動機になっています）．柏原・Schapiraではマイクロ台は「コホモロジーが伝播しない（余）方向」と表現されています．上記の条件は開集合への制限が同形になることを判定すればよいので，相対コホモロジーで書き下すことができそうです．しかもごく小さい近傍に一意に拡張できるという話なので，おさらいのところでも述べたように層バージョンの相対コホモロジーを使って，その茎を調べればよさそうです．というわけで正確には次のように定義ができます．
$F \in \Db(\bfk_X)$に対して，そのマイクロ台$\MS(F) \subset T^*X$を次のように定める．
$p \not\in \MS(F)$であるとは，$T^*X$内の$p$の開近傍$U$が存在して，任意の$x_0 \in X$と任意の$C^\infty$級函数$\varphi \colon X \to \bbR$で$d\varphi(x_0) \in U$を満たすものに対して
$$
\RG_{\{ x \in X \mid \varphi(x) \ge \varphi(x_0) \}}(F)_{x_0} \simeq 0
$$
を満たすことをいう．
別の言い方をすると，
$$
\MS(F):=
\overline{\left\{
(x_0;\xi_0) \; \middle| \;
\begin{split}
& \text{$\exists \varphi \colon X \overset{C^\infty}{\to} \bbR$ s.t. $d\varphi(x_0)=\xi_0$,} \\
& \RG_{\{ x \in X \mid \varphi(x) \ge \varphi(x_0) \}}(F)_{x_0} \not\simeq 0
\end{split}
\right\}}
\subset T^*X
$$
である．
以下しばしば簡単のため$\{ x \in X \mid \varphi(x) \ge \varphi(x_0) \}$を単に$\{\varphi \ge \varphi(x_0) \}$などとも書いてしまいます．完全三角を考えると$j \colon\{\varphi<\varphi(x_0)\} \hookrightarrow X$を開部分集合の埋め込みとして
$$
\RG_{\{\varphi \ge \varphi(x_0) \}}(F)_{x_0} \to F_{x_0} \to (Rj_*j^{-1}F)_{x_0} \to \RG_{\{\varphi \ge \varphi(x_0) \}}(F)_{x_0}[1]
$$
という$\Db(\bfk)$における完全三角が得られます．よって，$p \not\in \MS(F)$の条件は射$F_{x_0} \to (Rj_*j^{-1}F)_{x_0}$が同形であることと同値です．コホモロジーを取って帰納極限で表示すれば，任意の$n \in \bbZ$に対して，射
$$
\varinjlim_{x_0 \in B} H^n(B;F) \to \varinjlim_{x_0 \in B} H^n(\{\varphi<0\} \cap B;F)
$$
が同形であることと同値です．切除を考えればこれは射$\varinjlim_{x_0 \in B} H^n(\{\varphi<0\} \cup B;F) \to H^n(\{\varphi<0\};F)$が同形ということと同じなので，上の説明と整合性が取れました．
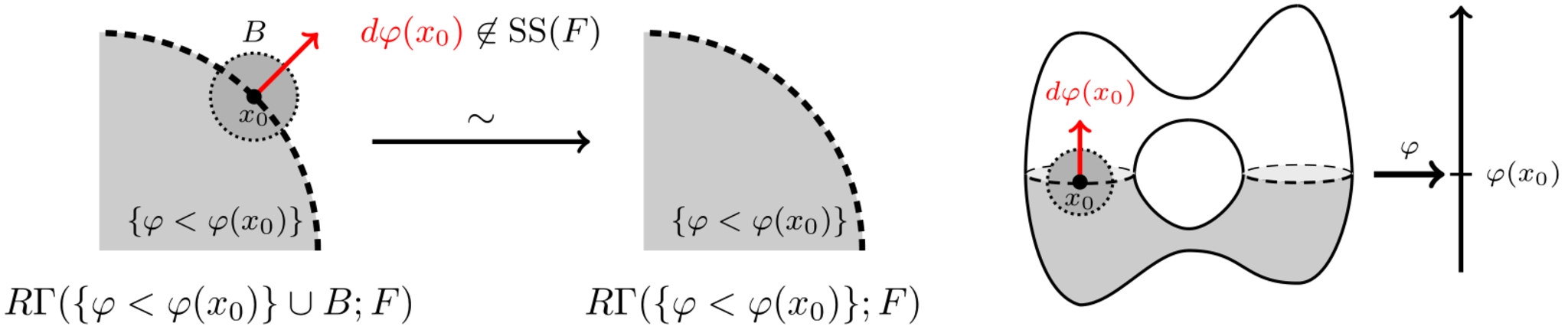マイクロ台の説明
上で見たようにマイクロ台の定義出てくる相対コホモロジー層の茎
$$
\RG_{\{ x \in X \mid \varphi(x) \ge \varphi(x_0) \}}(F)_{x_0} \in \Db(\bfk)
$$
はコホモロジーが同形に拡張されるための障害をあらわしています．$p$の方向に「壁」があってそれを$p$の方向にグッと押し出すことができるかというイメージを筆者は持っています．ここで「壁」という表現はSchapiraのノートから拝借しました．この障害をあらわす対象は結構大事で特性サイクルを考えるときにも出てきます．実はある条件のもとでは，函数$\varphi$から定まる適当な次数のシフトを施して$\RG_{\{\varphi \ge \varphi(x_0) \}}(F)_{x_0}[n_{\varphi,p}]$を考えると$\varphi$の取り方によらないことが分かるので，最近ではこれは$\phi_p(F)$とか$\mu_{p}(F)$などと書かれて$F$の$p$における超局所的茎 (microlocal stalk/microstalk) などと呼ばれています．Kashiwara-Schapiraでは（超局所的）タイプなどと呼ばれていました．
マイクロ台は柏原・Schapiraのもともとの呼称ではmicrosupportと呼ばれていた．何故$\MS$と書くかというと，もともと佐藤超函数の理論（ この記事 も参照）では，多様体$X$上の佐藤超函数$f$の方向別の特異性を調べるために余接束（またはその球面束）の部分集合である特異スペクトラム (singular spectrum) $\MS(f)$を定めてそれを調べていた（余談だがこれは$C^\infty$級超局所解析のwave front setに対応する）．この概念を函数ではなく層に対して定義したのが柏原とSchapiraであった．おそらく佐藤超函数理論に敬意を表して$\MS$と書かれていると思われる（著者の想像）．
しかしながら，近年は$\MS$という記号から逆にsingular support・特異台と呼ばれることも多い．数論幾何の分野でマイクロ台の類似物を研究している人々はほぼ特異台と呼んでいるように思われる．実はこの呼び方は佐藤超函数論での呼称と互換性がないのが問題である．佐藤超函数論では$f$の制限$f|_U$が実解析的になる最大の開部分集合$U$の補集合を特異台と呼んだ．すなわち，特異スペクトラムからゼロ集合を除いた$T^*X$の部分集合の$X$への射影の像$\pi(\MS(f) \setminus 0_X)$が特異台である．この名称と互換性を保つために「層$F$の特異台」で$\pi(\MS(F) \setminus 0_X)$を意味する人もいる（ほぼ特異台という語は使わないが使う場合は筆者もこの意味で使う）ため，呼称に混乱が生じている．
記号についても$\MS$のほかに$\mu \supp$や$\mu S$などといった記号も提案されているが，今だ定着したものはないように思われる．
マイクロ台の例を見る前にすぐに分かる性質について見ておきましょう．$0_X$または$T^*_XX$で余接束$T^*X$のゼロ切断をあらわします．
$F \in \Db(X)$とする．
(i) マイクロ台$\MS(F)$は$T^*X$内の閉錐状部分集合である．すなわち，閉部分集合であって$\bbR_{>0}$の作用で不変である．
(ii) $\MS(F) \cap 0_X = \Supp(F)$が成り立つ．
(iii) マイクロ台について三角不等式が成り立つ．すなわち，$F \to G \to H \to F[1]$を$\Db(\bfk_X)$の完全三角とするとき，$\MS(G) \subset \MS(F) \cup \MS(H)$が成り立つ．
(i) $p \not\in \MS(F)$の定義が開条件なので$\MS(F)$が閉部分集合であることが分かる．また$\MS(F)$の定義は方向だけを見ており$\bbR_{>0}$倍しても変わらないので，錐状であることも分かる．
(ii) $\varphi \equiv 0$と定数函数を取れば$\{ \varphi \ge \varphi(x_0) \}=X$であるから，相対コホモロジーの消滅条件は$F_{x_0} \simeq 0$となる．だいたいこのことから分かる．
(iii) $\RG_{\{ \varphi \ge \varphi(x_0) \}}(\ast)_{x_0}$を施すと完全三角
$$
\RG_{\{ \varphi \ge \varphi(x_0) \}}(F)_{x_0} \to \RG_{\{ \varphi \ge \varphi(x_0) \}}(G)_{x_0} \to \RG_{\{ \varphi \ge \varphi(x_0) \}}(H)_{x_0} \to \RG_{\{ \varphi \ge \varphi(x_0) \}}(F)_{x_0}[1]
$$
が得られる．$F$の項と$H$の項が消滅すれば$G$の項も消滅するので結論が得られる．
層のマイクロ台の例
それではいくつか層のマイクロ台の例を見てみましょう．
$F \in \Db(\bfk_X)$として任意の$n \in \bbZ$に対して$H^n(F) \in \Mod(\bfk_X)$が局所定数層であるとする．以降はこの条件を満たす導来圏の対象を単に局所定数層と呼ぶことにする．$F \neq 0$ならば，$F$のマイクロ台はゼロ切断，すなわち
$$
\MS(F)=0_X
$$
である．
実際このとき，函数$\varphi$が$d\varphi(x_0) \not\in 0_X$を満たすならば$\RG_{\{ \varphi \ge \varphi(x_0) \}}(F)_{x_0} \simeq 0$である．局所的なので定数層について考えればよいが，そのときはどの小さい開集合上の切断も同形であるからである．言い換えると局所定数層はどの方向にも同形に拡張することができるのでゼロ切断の外にはマイクロ台は現れない．
マイクロ台を使うことでうれしい点の一つはマイクロ台が層の形を決めてしまう場合があることです．層の形が分かっていれば，その相対コホモロジーを計算すればよいのでマイクロ台の形は分かるのは良いでしょう．大事なのはこの逆でマイクロ台が分かると層自体の形が制限されてしまう場合があります．これを使って，マイクロ台を知ることで層のことを知り層の様々な性質を引き出そうというのが超局所層理論の基本的なアプローチです．このタイプの主張の最初で最も簡単なものは次のもので，ある意味で上の例の逆が成り立つというものです．証明は次節の超局所的モースの補題を使いますのであとで概略を説明します．
$F \in \Db(\bfk_X)$とする．$\MS(F) \subset 0_X$ならば$F$は局所定数層である．
次に$X$の部分集合に台がある定数層（のゼロ拡張）のマイクロ台を考えましょう．$X$の閉部分多様体$M$に対して，$T^*_MX$で$M$に対する$X$内の余法束をあらわします．
$M$を$X$の閉部分多様体として，$M$上の定数層のゼロ拡張$\bfk_M \in \Db(\bfk_X)$を考える．このとき，$\bfk_M$のマイクロ台は$M$に対する$X$内の余法束，すなわち
$$
\MS(\bfk_M)=T^*_MX
$$
である．これは$M$に沿って動いても層は変わらないが，$M$から法方向に動くと茎が$\bfk$だったものが急に$0$に変化することを反映している．
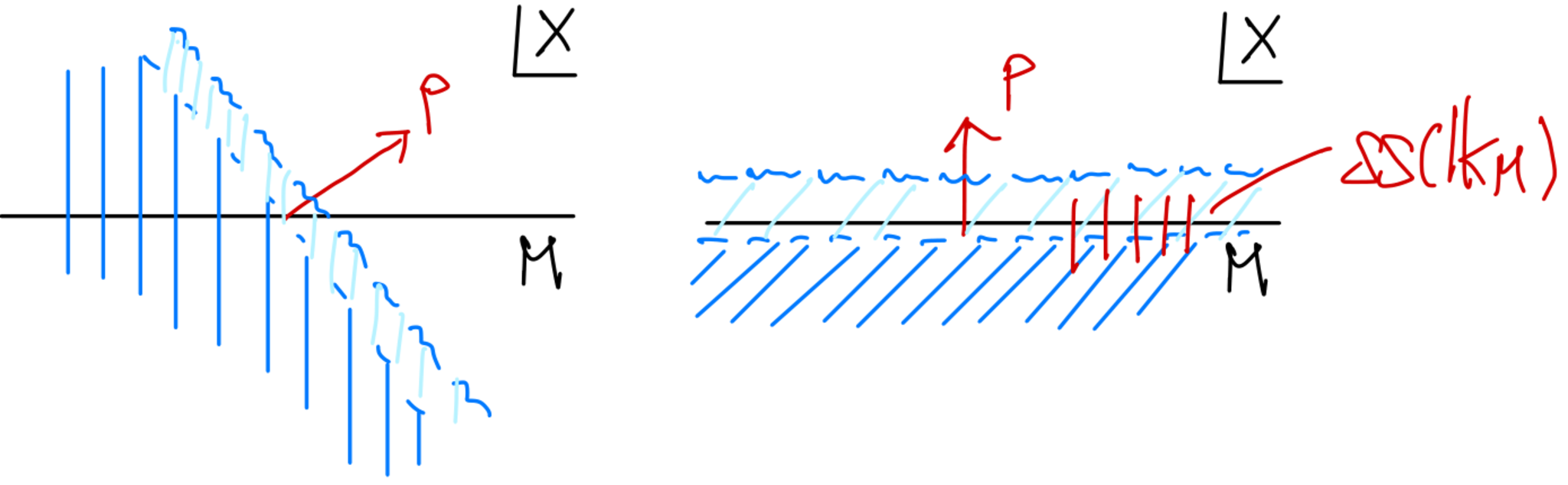閉部分多様体に台を持つ層のマイクロ台
これは局所的に相対コホモロジーを計算すればよい．局所的なので$X$がベクトル空間で$M$が部分ベクトル空間となるときを考えればよい．本質的な$X=\bbR^2, M=\{x_2=0\}$の場合を考えよう．まず$\{x_2=0\}$の外では$0$なので相対コホモロジーの茎も$0$でありマイクロ台はない．$p=(x_1,0;\xi_1,\xi_2) \in T^*\bbR^2$とする．$\xi_1 \neq 0$ならば$\Omega=\{ (y_1,y_2) \mid \langle (y_1-x_1,y_2), (\xi_1,\xi_2) \rangle <0 \}$は図3左のように斜めになっているので，ここに$M$の一部が含まれている．よって，$\RG(\Omega;\bfk_M) \simeq \bfk$であり$p$の方向に少しずらしても切断は変わらず同形である．しかし，$\xi_1=0$ならば$\Omega$は図3右のようになり$M$を含まないので$\RG(\Omega;\bfk_M) \simeq 0$となり，$p$の方向に少しでもずらすと切断は$\bfk$になって同形ではなくなってしまう．この考察からマイクロ台は$\{ (x_1,0;0,\xi_2) \}$という部分であることが分かり，これは余法束なのであった．
ベクトル空間内の閉凸錐に台を持つ層のマイクロ台を考えてみましょう．$E$をベクトル空間としたとき，部分集合$\gamma$が錐であるとは$\bbR_{>0}$の作用で閉じていることをいうのでした．$E$内の閉錐$\gamma$に対して，その双対錐 (dual cone) $\gamma^\circ$を
$$
\gamma^\circ := \{ \xi \in E^* \mid \langle \xi, v \rangle \ge 0 \ (v \in \gamma) \}
$$
で定めます．
$E$を有限次元ベクトル空間，$\gamma$を$E$の閉凸錐として$\bfk_\gamma \in \Db(\bfk_E)$を考える．このとき，
$$
\MS(\bfk_\gamma) \cap \pi^{-1}(0) = \gamma^\circ
$$
が成り立つ．
閉凸錐に台を持つ定数層のマイクロ台
これも上の例と同様に$p \in T^*E$に対して内積して$0$より小になる空間を考えてやれば議論は同様である．$p$の方向にその半空間をずらしたときに$\gamma$に侵入してしまう方向が$\gamma^\circ$だからである．
次はもう少し面白味がある例です．
$\Db(\bfk_\bbR)$の二つの対象$\bfk_{[0,1]}$と$\bfk_{[0,1)}$を考えよう．前者は閉区間$[0,1]$上の定数層のゼロ拡張であり，後者は半開区間$[0,1)$上の定数層のゼロ拡張である．これらのマイクロ台は以下の図5のようになる．
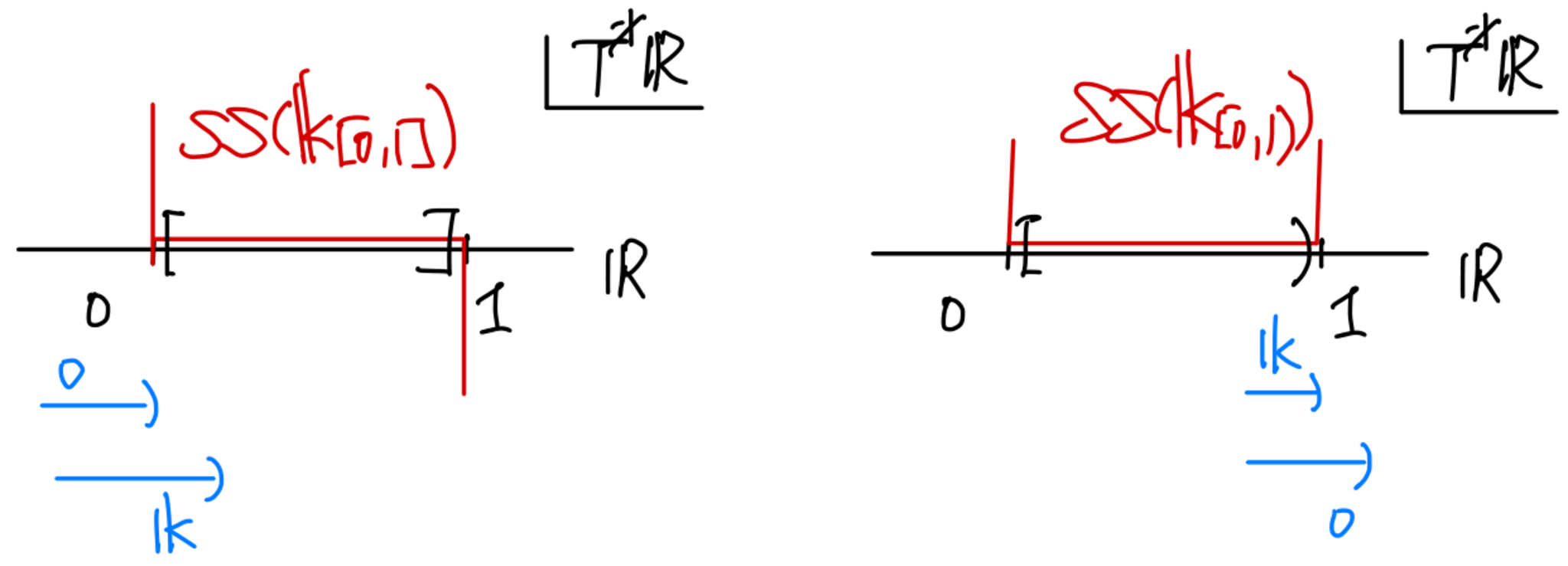区間上の定数層のゼロ拡張のマイクロ台
まず$F=\bfk_{[0,1]}$のマイクロ台を考えよう．ゼロ切断との共通部分に関しては命題2の(ii)から得られる．$0$のファイバーにおけるマイクロ台について考える．$(0;1)$がマイクロ台$\MS(F)$に入っているかどうか確認するには十分小さい$\varepsilon >0$に対して，切断の間の制限射
$$
\RG((-\infty,\varepsilon);F) \to \RG((-\infty,0);F)
$$
が同形であるかどうか調べればよい．$\RG((-\infty,\varepsilon);F) \simeq \bfk \ (0<\varepsilon<1)$であり$\RG((-\infty,0);F) \simeq 0$なので，上の制限射は同形ではなく$(0;1)$の方向には障害があり$(0;1) \in \MS(F)$である．一方で，$(0;-1)$については，制限射
$$
\RG((-\varepsilon,\infty);F) \to \RG((0,\infty);F)
$$
を考えればよい．これらはどちらも$\bfk$で射は恒等射と同一視できるので，$(0;-1)$の方向には障害がなく$(0;-1) \not\in \MS(F)$である．全く同様に考えると$1$のファイバーについても得られる．
次に$G=\bfk_{[0,1)}$のマイクロ台を考える．マイクロ台は局所的な概念なので$0$におけるファイバーについては$\bfk_{[0,1]}$の場合と同様である．$1$のファイバーについて考えよう．$(1;-1)$について見るために制限射
$$
\RG((1-\varepsilon, \infty);G) \to \RG((1,\infty);G)
$$
を調べると，$\RG((1-\varepsilon,\infty);G) \simeq 0, \RG((1,\infty);G) \simeq 0$なのでこれは同形である．実際，完全三角$\bfk_{[0,1)} \to \bfk_{[0,\infty)} \to \bfk_{[1,\infty)} \to \bfk_{[0,1)}[1]$の切断を考えると
$$
\RG((1-\varepsilon,\infty);G) \to \bfk \overset{\id}{\to} \bfk \to \RG((1-\varepsilon,\infty);G)[1]
$$
なる完全三角が得られるので$\RG((1-\varepsilon,\infty);G) \simeq 0$である．一方で，$\RG((-\infty,1);G) \simeq \bfk$であり$\RG((-\infty,1+\varepsilon);G) \simeq 0$なので，制限射
$$
\RG((-\infty,1+\varepsilon);G) \to \RG((-\infty,1);G)
$$
は同形ではない．実際，上でも見た完全三角に$\RG((-\infty,1+\varepsilon);\ast)$を施すと
$$
\RG((-\infty,1+\varepsilon);G) \to \bfk \overset{\id}{\to} \bfk \to \RG((-\infty,1+\varepsilon);G)[1]
$$
が得られるので，$\RG((-\infty,1+\varepsilon);G) \simeq 0$となることが分かる．したがって，$(1;1)$の方向には障害があり$(1;1) \in \MS(G)$となる．
上の例を一般化すると次のようになります．証明は上の議論をもっと精密にやることでできますが，ここでは省略します．
$\psi \colon X \to \bbR$を$C^\infty$級函数として，任意の$x \in \psi^{-1}(0)$に対して$d\psi(x) \neq 0$であると仮定する．このとき，$X$の閉部分集合$\{\psi \ge 0\}$と開部分集合$\{ \psi>0 \}$上の定数層のゼロ拡張のマイクロ台について
\begin{align}
\MS(\bfk_{\{\psi \ge 0\}}) & = \{ (x;\lambda d\psi(x)) \mid \lambda \psi(x)=0, \lambda \ge 0, \psi(x) \ge 0 \} \\
\MS(\bfk_{\{\psi > 0\}}) & = \{ (x;\lambda d\psi(x)) \mid \lambda \psi(x)=0, \lambda \le 0, \psi(x) \ge 0 \}
\end{align}
が成り立つ．式で書くと分かりづらいが，図は以下のようになる．ここで2次元空間の余接束はそのままでは図示できないので，各点でファイバーのどの方向にマイクロ台があるかを表示した．
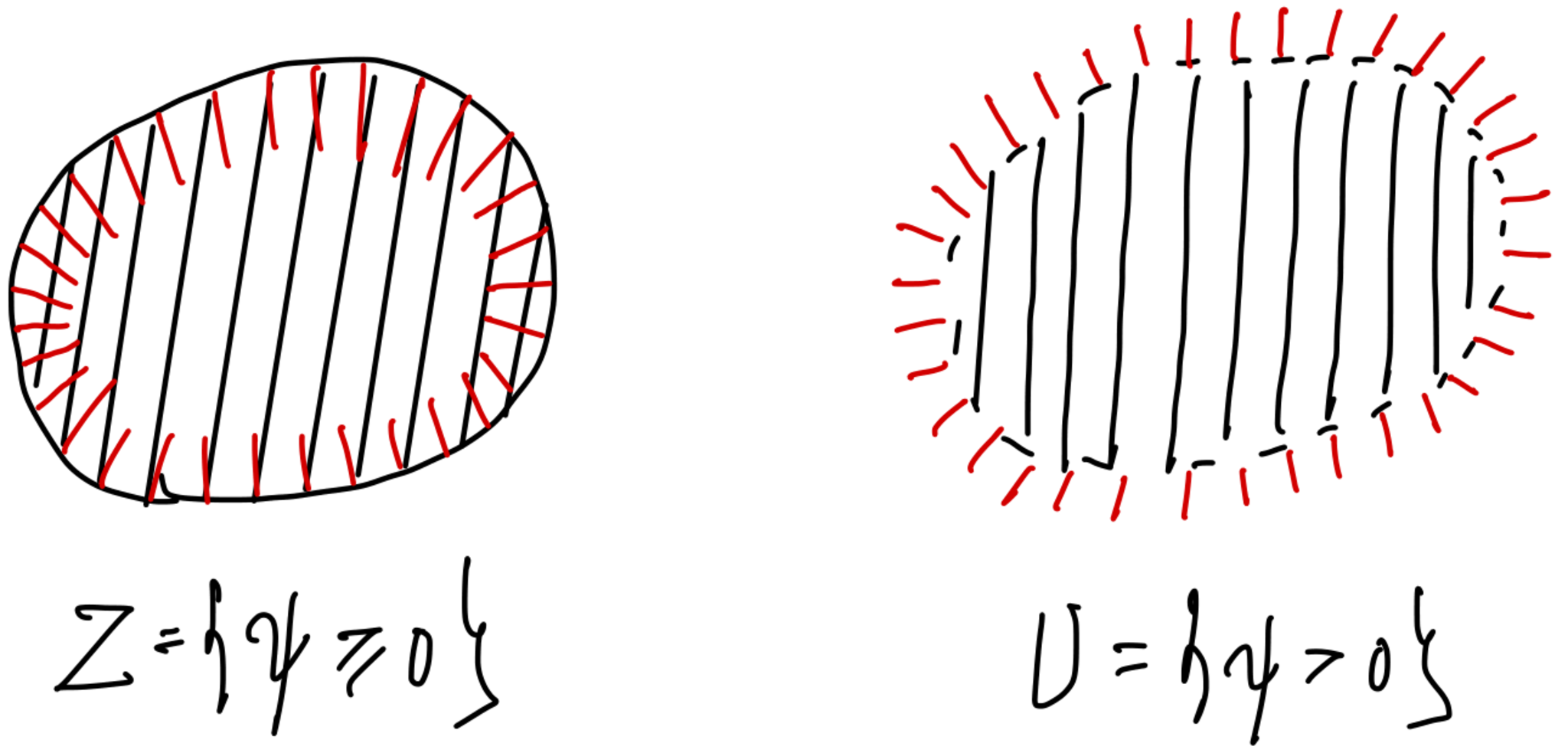閉集合と開集合上の定数層のゼロ拡張のマイクロ台
大事なことは，閉集合は境界でマイクロ台が内向きにあり，開集合は境界でマイクロ台が外向きにあるということである．上の$\bfk_{[0,1]}, \bfk_{[0,1)}$の例でもそのようになっている．
最後に$\cD$加群との関わりを述べておきます．$\cD$加群を知らない人は飛ばしてください．
$X$を複素多様体，$\cM$を連接$\cD_X$加群とする．このとき，$\cM$の解複体$\cRHom_{\cD_X}(\cM,\cO_X) \in \Db(\bbC_X)$のマイクロ台は$\cM$の特性多様体と一致する．すなわち，
$$
\MS(\cRHom_{\cD_X}(\cM,\cO_X))=\char(\cM)
$$
が成り立つ．これにより，$\cM$の解は特性多様体に入っていない方向に解析接続できることが分かる．
筆者は歴史のことは良く知らないのですが，おそらく上記のマイクロ台と特性多様体の一致がマイクロ台導入のきっかけになったものと思われます．もともと先に$\cD$加群の理論があって特性多様体も定義されていて，ホロノミー加群の解複体の構成可能性定理や解の解析接続に関する定理などに使われていたはずです．これら定理の証明を通して，一般の実多様体上の層に対してその特異性をあらわす余接束内の部分集合を定義しようとしたのだと思われます．
超局所的モースの補題
さて，上のたくさんの例からマイクロ台は層のコホモロジーの同形拡張の方向をあらわしていることがよくわかったと思います．しかし，もともとマイクロ台を導入した動機は「層に対する臨界点」を記述したいということでした．次の定理は超局所層理論の根幹をなす重要なもので，超局所的モースの補題 (microlocal Morse lemma) とか（もっと一般の主張として）非特性変形補題 (non-characteristic deformation lemma) と呼ばれています．
$F \in \Db(\bfk_X)$，$\varphi \colon X \to \bbR$を$C^\infty$級写像とする．さらに$a,b \in \bbR, a< b$とする．ここで次の二つを仮定する．
(1) $\varphi$は$\Supp(F)$上固有である．
(2) 任意の$x \in \varphi^{-1}([a,b))$に対して$d\varphi(x) \not\in \MS(F)$である．
このとき，劣位集合上の切断の間の制限射
$$
\RG(\varphi^{-1}((-\infty,b));F) \to \RG(\varphi^{-1}((-\infty,a));F)
$$
は同形である．
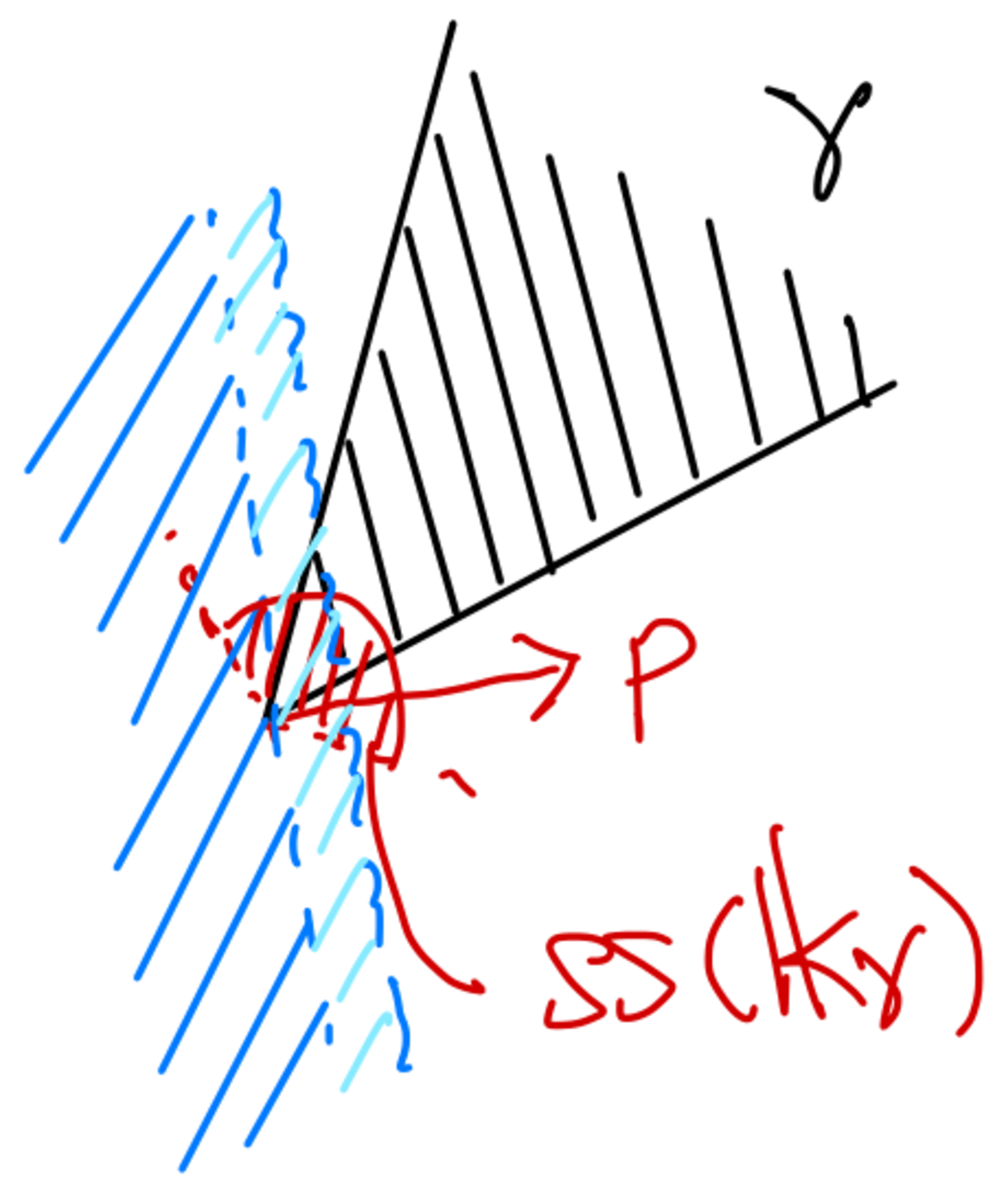
証明をちゃんとやるにはいろいろと必要なので気持ちだけ説明する．(2)の条件からレベル集合$\varphi^{-1}(a)$の各点$x$において$d\varphi(x)$はマイクロ台$\MS(F)$に属していないので，$\varphi^{-1}((-\infty,a))$上の切断はこの方向に同形に拡張できる．非常に雑には各点で拡張できるので，切断は$\varphi^{-1}((-\infty,a+\varepsilon))$まで同形に拡張できる．今度はレベル集合$\varphi^{-1}(a+\varepsilon)$で同じ議論をすればさらに同形に拡張していくことができる．これを繰り返して$\varphi^{-1}((-\infty,b))$上の切断まで到達する．
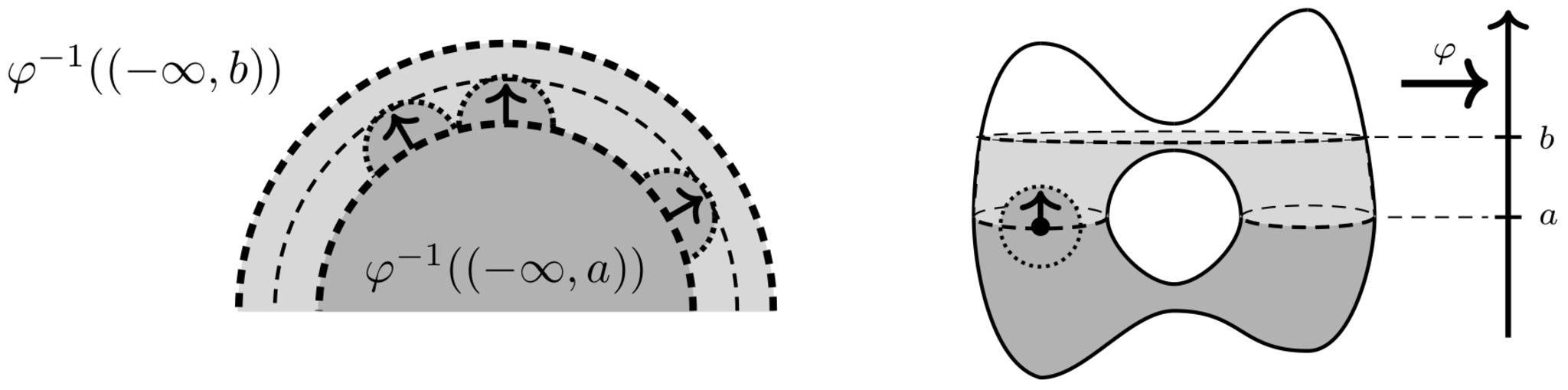超局所的モースの補題の証明の気持ち
実際の証明には上でごまかした$\varepsilon$延ばせるという部分を正確にするための帰納極限と逆極限を用いた同形の判定法および非ゼロの次数の下からの帰納法という柏原による巧妙な議論を用いる．この議論では帰納法を回すために下に有界であることが必要であったが，近年では帰納法に頼らない議論（Robalo-Schapiraを参照）が確立されたので非有界導来圏の対象に対しても適用可能になった．
$X$上の定数層$\bfk_X$に対して，超局所的モースの補題を適用するとどうなるか考えてみる．(1)の条件は$X$がコンパクトであることに対応する．上の例で見たように定数層のマイクロ台はゼロ切断なので，(2)の条件は区間$[a,b)$に$\varphi$の臨界値がないことに対応する．したがって，この場合は臨界値を越えない限り定数層のコホモロジーは同形のままであるという普通の古典的なモース理論（のコホモロジーに関する部分）を回復する．
こうしてマイクロ台が「層に対する臨界点」を記述するものだと確認できました．この定理は局所から大域へという層の基本方針をさらに推し進めて，超局所的な情報から大域的な情報を引き出せる点で非常に有用です．ここからも方向まで含めて解析するという超局所解析的な考え方が層と非常に相性が良いことが分かるでしょう．
マイクロ台を越える際のコホモロジーの挙動も層に対するモース不等式という形でとらえることができますが，それについては今回は説明しません．境界付き多様体$M$を境界のない多様体$X$の部分集合とみなして$\bfk_M \in \Db(\bfk_X)$に層に対するモース不等式を使うことで，境界付き多様体に対するモース不等式も直ちに得られることだけ述べておきます．
さて，最後に命題2の証明の概略を述べておきましょう．
各点$x_0 \in X$に対してある近傍$U$が存在して$x \in U$に対して$\RG(U;F) \to F_x$が同形であることを示せばよい．十分小さい近傍上で局所的に考えればよいのでユークリッド空間としてよい．$U$を$x_0$を中心とする十分小さい開球とする．すると任意の$x$に対して$C^\infty$球函数$\varphi \colon X \to \bbR$であって
(1) $\varphi(x)=0$,
(2) 任意の$y \neq x$に対して$\varphi(y) > 0$,
(3) $\varphi^{-1}((-\infty,1))=U$,
(4) 任意の$y \in \varphi^{-1}((0,1))$に対して$d\varphi(y) \neq 0$
となるものが存在する．$x_0$中心の十分大きな半径を持つ開球$B(x_0;R)$で台を切り落として$F$を取り換えることで初めから$\varphi$は$\Supp(F)$上固有であるとしてよい．$\MS(F) \subset 0_X$なので$\varphi$に対して超局所的モースの補題を適用できて
$$
\RG(U;F) \simto \RG(\varphi^{-1}((-\infty,\varepsilon));F)
$$
が十分小さい$\varepsilon>0$に対して成立する．よって，同形$\RG(U;F) \simto F_x$が成り立つ．
まとめ
今回は
- 層のマイクロ台の定義・超局所的な障害の捉え方
- マイクロ台の例
- 超局所的モースの補題・層に対する臨界点としての見方
について説明しました．超局所層理論はあんまり一気に書かないで小出しにしてゆっくり書いていこうと思います．次回は層の演算とマイクロ台との関係について説明したいと思います．それではまた！