保型形式の基礎のキソ:モジュラー形式とモジュラー群Γ
はじめに
この記事では保形形式のという大きな理論の一端であるモジュラー形式に焦点を当てて、その基本的な性質について解説していきます。
ここではモジュラー形式の基本的な理論についてを小難しく解説するだけなので応用的な話を知りたい人は
次回の記事
を参照してこの記事は読み飛ばしてもらってかまいません。
(追記)この記事はまだ私が初学者であったときに書いたものとなるので、色々と遠回りしているところがあります。また最近モジュラー形式の基礎理論についてもう少しちゃんとした記事を書きましたのでよければそちらもご参照ください。詳しくは
記事一覧
の「保型形式」の項をご覧ください。
モジュラー形式とは
$$SL(2,\Z)=\l\{\begin{pmatrix}a&b\\c&d\end{pmatrix}\Bigg|\;a,b,c,d\in\Z,\;ad-bc=1\r\}$$
の元$\g$と複素数$z$に対して作用$\g z$を
$$\g z=\frac{az+b}{cz+d}\qquad(\g=\begin{pmatrix}a&b\\c&d\end{pmatrix})$$
と定める。これによって定まる写像
$$\ol\g:\C\to\C\quad z\mapsto\g z$$
のことを一次分数変換、あるいはメビウス変換と言う。
また$SL(2,\Z)$が定める一次分数変換のなす群
$$\G=SL(2,\Z)/\{\pm I\}$$
のことをモジュラー群という。
以下、行列$\g$と一次分数変換$\ol\g$を同一視して考える。つまり符号の差を無視して$\g=-\g$とみなすことに注意する。
上半平面
$$\H=\{z\in\C\mid\Im(z)>0\}$$
上の関数$f$であって次の条件を満たすもののことを重さ$k$の(正則)モジュラー形式という。
- $f$は$\H$上正則である
- $f$は$\g\in\G$の作用に対して等式
$$f\l(\frac{az+b}{cz+d}\r)=(cz+d)^kf(z)\qquad(\g=\begin{pmatrix}a&b\\c&d\end{pmatrix})$$
を満たす。 - $f$はカスプ$z=i\infty$においても正則である(この意味については後で述べる)。
また$\H\cup\{i\infty\}$上有理型で$\G$の作用に対して不変(つまり重さ$0$)なる関数をモジュラー関数と言います。
いま重さ$k$のモジュラー形式$f$に対し
$$f(z)=f(\M{-1}00{-1}z)=(-1)^kf(z)$$
が成り立つことから$k$が奇数のときは$f(z)=0$となるので以下$k$は偶数であるものとします。
$\G$の$\H$への作用について
上半平面の点$z$の一次分数変換は再び上半平面の点となることは
\begin{eqnarray}
\farc{az+b}{cz+d}
&=&\frac{(az+b)(c\ol z+d)}{|cz+d|^2}=\frac{a|z^2|+adz+bc\ol z+bd}{|cz+d|^2}
\\&=&\frac{a|z^2|+bc(z+\ol z)+bd}{|cz+d|^2}+\frac{z}{|cz+d|^2}\quad(\because ad=bc+1)
\end{eqnarray}
より
$$\Im\l(\farc{az+b}{cz+d}\r)=\farc{\Im(z)}{|cz+d|^2}>0$$
とわかります。
カスプでの挙動について
モジュラー形式は
$$f(\M1101z)=f(z+1)=f(z)$$
という周期性を持つのでフーリエ級数展開
$$f(z)=\sum^\infty_{n=-\infty}c_ne^{2\pi inz}$$
を持つことになります。このとき
$$g(w)=\sum^\infty_{n=-\infty}c_nw^n$$
によって定まる関数が$w=0$において正則となることを$f$はカスプ$z=i\infty$において正則であると言います。
特にカスプでの正則性と
- 負の項$c_{-n}$が全て$0$となること
- $\Im(z)\to\infty$における極限$f(z)\to f(i\infty)\quad(=c_0)$が存在すること
は同値であることに注意しましょう。
またカスプにおいて$0$になる(つまり$c_0=0$となる)モジュラー形式のことをカスプ形式と言います。更に$g(w)$が$w=0$を$m$位の零点に持つ、つまり
$$f(z)=\sum^\infty_{n=m}c_ne^{2\pi inz}\quad(c_m\neq0)$$
が成り立つとき、$f$はカスプ$z=i\infty$を$m$位の零点に持つと言います。
$f$がカスプにおいて有理型であることや極を持つことについても同様に定義されます。
$q$-展開
いまカスプでの正則性からモジュラー形式$f$は
$$f(z)=\sum^\infty_{n=0}c_ne^{2\pi inz}$$
と表せるのでした。このとき$q=e^{2\pi iz}$と置き換えた
$$f(z)=\sum^\infty_{n=0}c_nq^n$$
という表示のことを$f$の$q$-展開と言います。
ちなみにモジュラー関数の$q$-展開は有限個の負の指数の項を許した
$$f(z)=\sum^\infty_{n=-m}c_nq^n$$
という形になっています。
モジュラー群の構造
モジュラー形式を考えていくにあたって先にモジュラー群の構造について触れておきます。
モジュラー群の分解
モジュラー群$\G$は$SL(2,\Z)/\{\pm I\}$と同型である。
常々暗黙の了解として認められている事実ですがちゃんと確かめておきましょう。
$SL(2,\Z)$の$\G$の対応$\g\mapsto\g$が準同型となること、つまり$\g,\g'\in\G$に対して一次分数変換としての合成$\g\circ\g'$と行列としての積$\g\g'$が等しいことを示せばよい。
そのことは
\begin{align}
\M abcd(\M efghz)&=\frac{\dis a\frac{ez+f}{gz+h}+b}{\dis c\frac{ez+f}{gz+h}+d}\\
&=\frac{a(ez+f)+b(gz+h)}{c(ez+f)+d(gz+h)}\quad\cdots(\bigstar)\\
&=\frac{(ae+bg)z+(af+bh)}{(ce+dg)z+(cf+dh)}\\
&=\M{ae+bg}{af+bh}{ce+dg}{cf+dh}z\\
&=(\M abcd\M efgh)z
\end{align}
とわかる。
$(\bigstar)$の式がまさに行列の積って感じで面白いですよね。
モジュラー群$\G$は$2$つの行列
$$\M1101,\M0{-1}10$$
によって生成される。
行列
$$\M abcd$$
に対し$c$についての数学的帰納法で示す。
いま$\g=-\g$とみなしていたことに注意する。
$c=0$のとき
$ad-bc=ad=1$より$a=d=\pm1$なので
$$\M1b01=\M1101^b$$
と主張を得る。
$c=1$のとき
$ad-bc=ad-b=1$より$b=ad-1$なので
$$\M a{ad-1}1d=\M1a01\M0{-1}10\M1d01$$
であり、$c=0$のときと合わせて主張を得る。
$c\geq2$のとき
$ad-bc=1$より$\gcd(c,d)=1$であることに注意すると
$$d=cq+r\quad(q\in\Z,1\leq r< c)$$
と表せ、このとき
$$\M abcd\M1{-q}01\M0{-1}10=\M{-aq+b}{-q}r{-c}$$
なので数学的帰納法により主張を得る。
モジュラー群を生成する$2$つの行列
$$\M1101,\M0{-1}10$$
はそれぞれ平行移動$z\mapsto z+1$と反転$z\mapsto-\farc1z$という変換に対応しています。
(厳密には反転ではなく反転$\times$虚軸対称という変換ですが個人的な好みで単に反転と呼ぶことにしています。)
この"平行移動"と"反転"というキーワードは今後しばしば出てくるのでよく覚えておいてください。
関数$f$が
$$f(z+1)=f(z),\quad f\l(-\frac1z\r)=z^kf(z)$$
を満たせば$\G$の$f$への作用に対して
$$f\l(\farc{az+b}{cz+d}\r)=(cz+d)^kf(z)$$
が成り立つ。
行列
$$\g=\M abcd$$
に対して$j(\g,z)=cz+d$とおくと仮定の式は
$$\s_1=\M1101,\quad\s_2=\M0{-1}10$$
を用いて
$$f(\s_1z)=j(\s_1,z)^kf(z),\quad f(\s_2z)=j(\s_2,z)^kf(z)$$
と表せる。つまり命題2によって$\g\in\G$を$\s_1$と$\s_2$の積$\g_1\g_2\cdots\g_n$に分解したとき
\begin{eqnarray}
f(\g z)&=&f(\g_1(\g_2\g_3\cdots\g_nz))
\\&=&j(\g_1,\g_2\g_3\cdots\g_nz)^kf(\g_2(\g_3\cdots\g_nz))
\\&=&j(\g_1,\g_2\g_3\cdots\g_nz)^kj(\g_2,\g_3\cdots\g_nz)^kf(\g_3\cdots\g_nz)
\\&&\quad\quad\quad\quad\vdots
\\&=&\l(\prod^n_{k=1}j(\g_k,\g_{k+1}\cdots\g_nz)\r)^kf(z)
\end{eqnarray}
となるので
$$j(\g,z)=\prod^n_{k=1}j(\g_k,\g_{k+1}\cdots\g_nz)$$
が成り立つことを示せればよい。実際には$\g,\g\in\G$に対して
$$j(\g\g,z)=j(\g,\g z)j(\g,z)$$
が成り立つことを示せば十分である。
そしてそれは
$$\g=\M abcd,\g'=\M efgh$$
とおくと
\begin{eqnarray}
j(\g,\g'z)j(\g',z)
&=&(c\frac{ez+f}{gz+h}+d)(gz+h)
\\&=&c(ez+f)+d(gz+h)
\\&=&(ce+dg)z+(cf+dh)
\\&=&j(\g\g',z)
\end{eqnarray}
とわかる。
基本領域
上半平面$\H$の元$z,w$に対して同値関係$\sim$を
$z\sim w\iff\exists\g\in\G,\;w=\g z$
と定め、$\G$に対する$\H$の基本領域$D$を$D=\H/\sim$と定める。
慣例として基本領域$D$は上半平面$\H$をモジュラー群$\G$で左から割ったものという意味で
$$D=\G\backslash\H$$
と書かれます。
また基本"領域"と名にある通り$D$は各同値類から適当に代表元を取り$\H$内の領域とみなしたものであり
- $\forall z\in\H,\;\exists w\in D,\;\exists\g\in\G,\;z=\g w$
($\H$の任意の点は$D$のある点の一次分数変換として表せれるということ) - $\forall z,w\in D\;[\exists\g\in\G,\;z=\g w\Rightarrow z=w]$
($D$の任意の点はその一次分数変換によって$D$の別の点を表すことはないということ)
という性質を満たすものとして特徴づけられる領域となります。
具体的にどのような領域になるのかは以下の命題で記述されます。
基本領域$D$は
$y>\sqrt{1-x^2}\quad(-\frac12\leq x<\frac12)$
または
$y=\sqrt{1-x^2}\quad(-\frac12\leq x\leq0)$
を満たす複素数$z=x+iy$全体の集合に一致する。
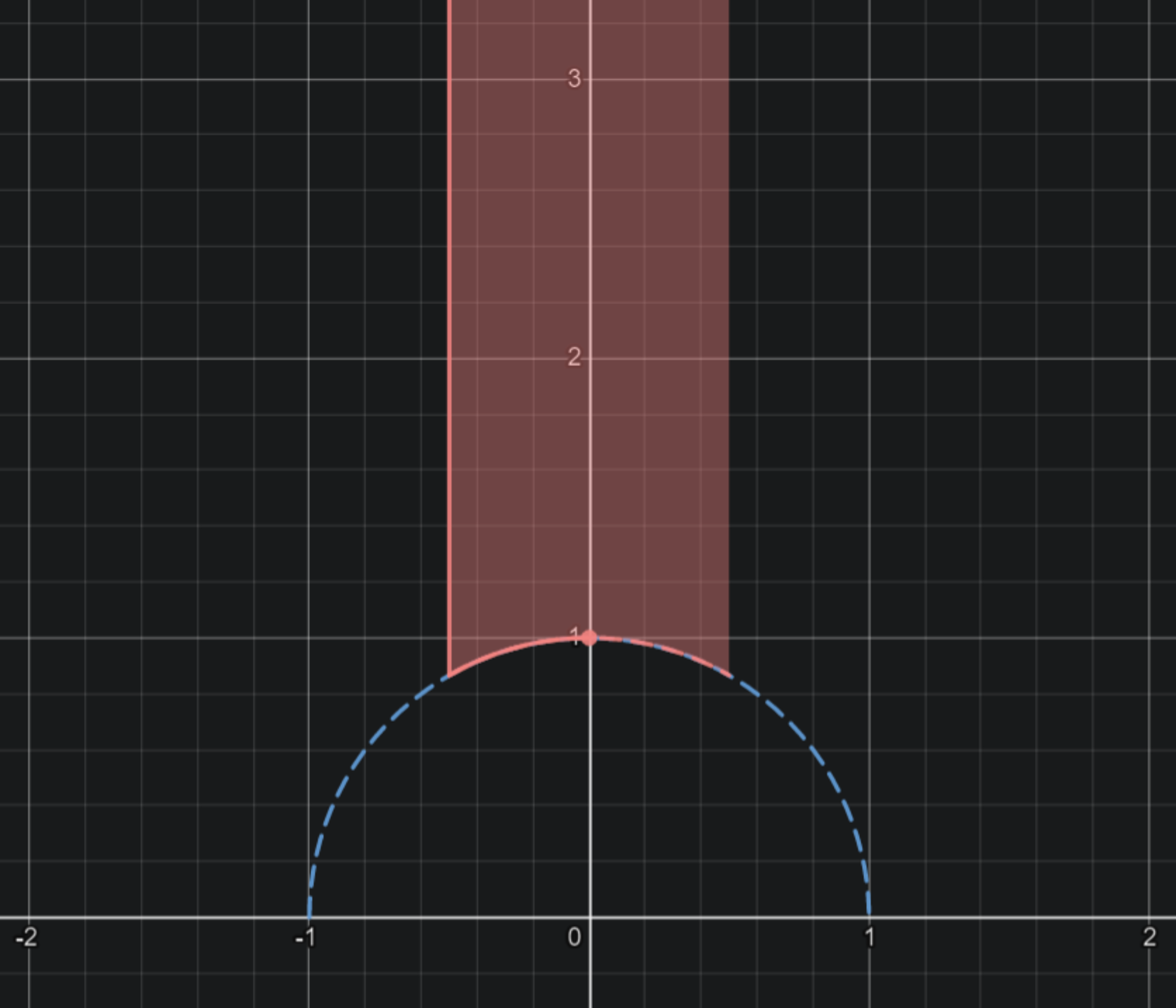 複素数平面における基本領域の図
複素数平面における基本領域の図
主張のような領域を$D'$とおいたとき
$(\mathrm{i})$任意の$z\in\H$に対してある$w\in D'$と$\g\in\G$があって$w=\g z$
$(\mathrm{ii})$任意の$z\in D',\;\g\in\G$に$\g z\in D'$ならば$\g z=z$
が成り立つことを示せばよい。
$(\mathrm{i})$の証明
$$\g=\M abcd\in\G$$
について上の方で示した通り
$$\Im(\g z)=\frac{\Im(z)}{|cz+d|^2}$$
が成り立っていたので$\Im(\g z)$が最大(つまり$|cz+d|$が最小)となるような$c,d$が取れ、そのような$\g$に対し
$$-\frac12\leq\Re(\g z+n)<\frac12$$
なる整数$n$を取って
$$\g'=\M 1n01\g$$
とおく。
このとき$\g$の取り方から
$$\Im(\M 0{-1}10\g'z)=\Im\l(-\frac1{\g'z}\r)=\farc{\Im(\g'z)}{|\g'z|^2}\leq\Im(\g'z)$$
でなければならない、つまり$|\g'z|\geq1$なので$\g'z\in D'$を得る。
($|\g'z|=1$かつ$0<\Re(\g'z)<\frac12$のときは$\g''=({}^0_1{}^{-1}_{\;\,0})\g'$とおけば$\g''z\in D'$がわかる。)
$(\mathrm{ii})$の証明
$z,\g z\in D'$に対して一般性を失わずに$\Im(z)\leq\Im(\g z)$としてよい。
($\Im(z)>\Im(\g z)$のときは$z=\g^{-1}(\g z)$より$\g^{-1},\g z$と改めて$\g,z$とおけばよい。)
このとき$\g=(\substack{a\;b\\c\;d}),\;z=x+iy\;(x,y\in\R)$とおくと
$$\Im(z)\leq\Im(\g z)=\frac{\Im(z)}{|cz+d|^2}$$
つまり$|cz+d|^2\leq1$から$x^2+y^2\geq1,\;|x|\leq\frac12$に注意すると
\begin{eqnarray}
1&\geq&|cz+d|^2=c^2(x^2+y^2)+2cdx+d^2
\\&\geq&c^2-|cd|+d^2=(|d|-\frac12|c|)^2+\farc34c^2
\\&\geq&\frac34c^2
\end{eqnarray}
なので$c\in\Z$に注意すると$c=0,\pm1$でなければならない。
($c=-1$の場合は$c=1$の場合に帰着するので考える必要はないことに注意する。)
- $c=0$のとき
$ad-bc=ad=1$より$a=d=\pm1$なので
$$\g z=\pm\M1b01z=z+b$$
であり、$-\frac12\leq \Re(z),\Re(\g z)<\frac12$に注意すると$b=0$でなければならず
$\g z=z$
を得る。 - $c=1$のとき
$1\geq|cz+d|=|z+d|$なのでそのような$z\in D',d\in\Z$の取り方は
$d=0$かつ$|z|=1$かつ$-\frac12\leq x\leq0$
または
$d=1$かつ$\dis z=\o=\frac{-1+\sqrt3i}{2}$
に限られる。(上の図1をよく見てもらうとわかると思う。)- $d=0$のとき
$ad-bc=-b=1$より
$$\g z=\M a{-1}10z=\farc{az-1}{z}=a-\frac1z\in D'$$
であるが、そのような$a\in\Z,z\in D'\;(|z|=1)$の取り方は
$(a,z)=(0,i),(-1,\o)$
に限られ、どちらの場合も
$\dis\g z=a-\frac1z=z$
が成り立っていることがわかる。 - $d=1$のとき
$ad-bc=a-b=1$なので($\o^2+\o+1=0$より)$\o+1=-\o^{-1}$に注意すると
$$\g z=\M a{a-1}11\o=\frac{a(\o+1)-1}{\o+1}=a+\o\in D'$$
であり、そのような$a\in\Z$の取り方は$a=0$に限られ、
$\g z=\o=z$
を得る。
- $d=0$のとき
重さ$0$のモジュラー形式
次にモジュラー形式の理論で最も重要な命題の一つである次の主張を紹介しておきます。
重さ$0$の正則モジュラー形式は定数関数に限る。
重さ$0$のモジュラー形式$f$は$D$上正則で、$z=i\infty$においても発散しないので連続関数$|f(z)|$は$D$上か$z=i\infty$において最大値を取る(重さ$0$という条件よりこれは$\H\cup\{i\infty\}$上の最大値となる)。また$f(z)-f(i\infty)$を再び$f(z)$とおくことで$|f(z)|$は$z=i\infty$で最大値を持たないものとしてよい。
このとき$|f(z)|$は$z=z_0\in D$で最大値を取ることになるが、$\H$における$z=z_0$の近傍で最大値の原理(開領域上(定数関数でない)正則な関数の絶対値はその領域の内部で最大値を取ることはない)を適用することで$f$は定数関数でなければならないことがわかる。
また命題5はコンパクトリーマン面上のリウヴィルの定理を使っても証明されます。
コンパクトリーマン面上正則な関数は定数関数に限る。
コンパクトリーマン面$M$上正則な関数$f$について$M$のコンパクト性から連続関数$|f(z)|$はある点$z=z_0\in M$で最大値を取る。このとき($M$がリーマン面であることから)$z_0\in M$の開近傍から$\C$の開領域(もしくは開単位円盤)$D$への同相写像$\phi$であって$f(\phi^{-1}(z))$が$D$上正則となるようなものが存在するが、$|f(\phi^{-1}(z))|$は$D$の内部の点$z=\phi(z_0)$で最大値を取ることになり最大値の原理からそのような$f$は定数関数に限ることがわかる。
$D\cup\{i\infty\}$がコンパクトリーマン面であることは こちらの記事 などを見てみるとわかりやすいと思います。
モジュラー形式の特殊な零点
重さ$k$のモジュラー形式$f$はある一次分数変換に対して不変、つまり
$$\a=\frac{a\a+b}{c\a+d}$$
を満たす$\a\in\H$に対して
$$f(\a)=f\l(\frac{a\a+b}{c\a+d}\r)=(c\a+d)^kf(\a)$$
が成り立つのでもし$(c\a+d)^k\neq1$ならば$f(\a)=0$となることがわかります。
そのような$\a$としてはどのようなものが取れるのか以下で見てみましょう。
ある$\g\in\G$の作用に対して不変な$\a\in\H$は
$$\a=\farc{-d+i}{c}\quad(c|(d^2+1),c>0)$$
または
$$\a=\frac{-2d\pm1+\sqrt3i}{2c}\quad(c|(d^2\mp d+1),c>0)$$
と表されるもので尽くされる。
いま$z$についての方程式
$$z=\frac{az+b}{cz+d}$$
つまり$cz^2-(a-d)z-b=0$の解が虚数解を持つためには$ad-bc=1$に注意すると
\begin{align}
0&>(a-d)^2+4bc\\
&=(a-d)^2+4(ad-1)\\
&=(a+d)^2-4
\end{align}
となることが必要十分であり、$a+d$は整数であること注意すると
$$|a+d|=0,1$$
の二通りに分けられる。
また適当に符号を取り換えることで$c>0$としてよく、このとき$z\in\H$なる解は
$$z=\frac{a-d+\sqrt{4-(a+d)^2}i}{2c}$$
と求まることに注意する。
$|a+d|=0$のとき
$|a+d|=0$つまり$a=-d$のときは
$$z=\frac{-d+i}{c}$$
と求まる。
またこのとき
$$bc=ad-1=-(d^2+1)$$
より$c\mid(d^2+1)$が成り立つ。
$|a+d|=1$のとき
$|a+d|=1$つまり$a=-d\pm1$のときは
$\dis z=\frac{-2d\pm1+\sqrt3i}{2c}$
と求まる。
またこのとき
$$bc=ad-1=-(d^2\mp d+1)$$
より$c\mid(d^2\mp d+1)$が成り立つ。
\begin{align}
z_4&=\farc{-d+i}{c}&&(c|(d^2+1),c>0)\\
z_3&=\frac{-2d-1+\sqrt3i}{2c}&&(c|(d^2+d+1),c>0)\\
z_6&=\frac{-2d+1+\sqrt3i}{2c}&&(c|(d^2-d+1),c>0)
\end{align}
とおくと重さ$k$のモジュラー形式$f(z)$は
・$4\nmid k$のとき$z=z_4$
・$6\nmid k$のとき$z=z_3,z_6$
を零点に持つ。
上で見たように適当な$a,b$に対して$z=z_n\;(n=3,4,6)$は
$$f(z_n)=f\l(\frac{az_n+b}{cz_n+d}\r)=(cz_n+d)^kf(z_n)$$
を満たし、
\begin{align}
\z_4&=cz_4+d=i\\
\z_3&=cz_3+d=\farc{-1+\sqrt3i}2\\
\z_6&=cz_6+d=\frac{1+\sqrt3i}2
\end{align}
はそれぞれ$1$の原始$n$乗根$\z_n=e^{\frac{2\pi i}n}$であるので$n\ndiv k$において$$(cz_n+d)^k=\z_n^k\neq1$$
となり$f(z_n)=0$を得る。
($k$は偶数としていたので$3\nmid k\iff6\nmid k$が成り立つことに注意する。)
$\z_n$の最小多項式(円分多項式)を$\Phi_n(x)$とおくと
$$z_n=\frac{\z_n-d}{c}\quad(c\mid\Phi_n(d),c>0)$$
という形になっているのが面白いですね。また$d=0,c=1$としたとき以下の系が得られます。
重さ$k$のモジュラー形式$f(z)$は$n\nmid k\;(n=3,4,6)$のとき$z=\z_n$を零点に持つ。
逆に$k$が$4,6$の公倍数、つまり$12$の倍数であるとき$f(z)$はこのような、いわゆる自明な零点を持たないことになります。
次回の記事
ではラマヌジャンのデルタという重さ$12$の特別なモジュラー形式が活躍しますが、ラマヌジャンのデルタが特別である所以は初めて自明な零点を持たない重さが$12$であることにもあるように思えます。
