高校数学から始める数値計算(1):補間多項式
目次
本稿は「1. はじめに」と「2. 補間多項式」に当たります.なお,本稿はこの PDF版 を元に,Mathlogの仕様に合わせて一部の文言・体裁を変更したものです.内容は変わりません.
はじめに
計算機上で関数を扱うには,関数をよく知られた扱いやすい関数で近似できると何かと便利である.中でも扱いやすい関数は多項式関数であろう.$+$と$\times$の2つの演算さえ実行できれば計算でき,しかも,曲線として表現できる幅もそれなりに広い.本稿では,この多項式関数によって,種種の計算を近似的に行う方法を紹介する.
ラグランジュ補間
次の定理は,本稿を通して重要な役割を担うものである.
実数の組$P_1 = (p_1, q_1), \dots, P_n = (p_n, q_n)$は,$i \neq j$なら必ず$p_i \neq p_j$を満たすとする.このとき,任意の$i = 1,\dots,n$について変数$x$に$p_i$を代入した値が$q_i$であり,かつ次数が$n-1$以下である多項式$f(x)$がただ1つ存在する.
まず存在性を示す.$i=1,\dots,n$に対し,多項式$g_i(x)$を
$$
g_i(x) = (x-p_1) \cdots (x-p_{i-1})(x-p_{i+1}) \cdots (x-p_n)
$$
で定義する.このとき
$$
g_i(p_j) = {
\begin{cases}
(p_j-p_1) \cdots (p_j-p_{i-1})(p_j-p_{i+1}) \cdots (p_j-p_n) & (j = i) \\
0 & (j \neq i)
\end{cases}
\quad
(j = 1,\dots,n)
}
$$
である.仮定により$i \neq j$なら$p_i \neq p_j$なので,$g_i (p_i) \neq 0$である.したがって
$$
f(x) = q_1h_1(x) + \cdots + q_nh_n(x),
\quad
h_i(x) = \frac{1}{g_i(p_i)} g_i(x)
$$
により多項式$f(x), h_1(x), \dots, h_n(x)$を定義すれば
\begin{align*}
f(p_i)
&= q_1h_1(p_i) + \cdots + q_nh_n(p_i) \\
&= q_10 + \cdots + q_{i-1}0 + q_i\pqty{\frac{1}{g_i(p_i)} g_i(p_i)} + q_{i+1}0 + \cdots + q_n0 \\
&= q_i
\end{align*}
となる.$h_1(x), \dots, h_n(x)$の次数は$n-1$次なので,これらの定数倍の和である$f(x)$の次数は最大でも$n-1$である.
次に一意性を示す.多項式$f_1(x), f_2(x)$はともに次数が$n-1$以下であり,かつすべての$i = 1, \dots, n$に対して$q_i = f_1(p_i) = f_2(p_i)$を満たすとする.$g(x) = f_1(x) - f_2(x)$で多項式$g(x)$を定義すると,$g(x)$の次数も$n-1$以下である.また,$x = p_1, \dots, p_n$のとき$g(x) = 0$であり,$p_1,\dots,p_n$はどの2つも相異なるので,因数定理により$g(x)$は$x-p_1,\dots,x-p_n$を因数に持つ.すなわち,$g(x)$は多項式$A(x)$によって
$$
g(x) = A(x)(x-p_1) \cdots (x-p_n)
$$
と書ける.$g(x)$の次数は$n-1$以下なので,この等式が成り立つには$A(x) = 0$でなければならない.よって$g(x) = 0$であるので,$f_1(x) = f_2(x)$が示された.
定理1の多項式$f(x)$をラグランジュの補間多項式(あるいは単に補間多項式)という.
$f(x)$は次のように表せる.
$$
f(x) = \sum_{i=1}^n q_i \prod_{k\neq i} \frac{x - p_k}{p_i - p_k}
$$
$\prod$は総乗記号であり,$\sum$の$+$を$\times$に置き換えたものである.この場合は$k=1,\dots,i-1,i+1,\dots,n$について積をとる.
$(p_1,q_1)=(1,4),(p_2,q_2)=(3,0),(p_3,q_3)=(4,1)$のとき,補間多項式は
$$
f(x)
= 4\cdot\frac{(x-3)(x-4)}{(1-3)(1-4)} + 0\cdot\frac{(x-1)(x-4)}{(3-1)(3-4)} + 1\cdot\frac{(x-1)(x-3)}{(4-1)(4-3)}
= x^2-6x+9
$$
である.
$(p_1,q_1)=(1,6),(p_2,q_2)=(5,2),(p_3,q_3)=(4,3)$のとき,補間多項式は
$$
f(x)
= 6\cdot\frac{(x-5)(x-4)}{(1-5)(1-4)} + 2\cdot\frac{(x-1)(x-4)}{(5-1)(5-4)} + 3\cdot\frac{(x-1)(x-5)}{(4-1)(4-5)}
= -x+7
$$
である.このように,$n$個の点に関する補間多項式の次数は必ずしも$n-1$にならない.
 点と補間多項式の関係
点と補間多項式の関係
ニュートン補間
この節では,補間多項式が通るべき点を追加したとき,補間多項式はどう変化するか考える.
定理1の状況で,$k=1,\dots,n$に対して,点$P_1,\dots,P_k$に関する補間多項式を$f_k(x)$とする.
$g_k(x) = f_k(x) - f_{k-1}(x)$とおくと,$i = 1,\dots,k-1$について$g_k(p_i)=0$である.$g_k(x)$の次数は最大でも$k-1$なので,因数定理により
$$
g_k(x) = A_{k-1}(x-p_1)\cdots (x-p_{k-1})
$$
を満たす実数$A_{k-1}$が存在する.
したがって
\begin{align*}
f_n(x) - f_{n-1}(x) &= A_{n-1}(x-p_1)\cdots (x-p_{n-2})(x-p_{n-1}) \\
f_{n-1}(x) - f_{n-2}(x) &= A_{n-2}(x-p_1)\cdots (x-p_{n-2}) \\
&\vdots \\
f_2(x) - f_1(x) &= A_1(x-p_1) \\
f_1(x) &= q_1
\end{align*}
である.すべて足すことで
$$
f(x) = f_n(x) = q_1 + \sum_{k=1}^{n-1} A_k(x-p_1)\cdots (x-p_k)
$$
を得る.以上により,定義1の補間多項式$f(x)$は,$n-1$個の実数$A_1,\dots,A_{n-1}$により上のように表せることが分かる.また,この式に現れる$\sum$を$k=l-1$までで打ち切った多項式は$f_l(x)$であり,点$P_1,\dots,P_l$に関する補間多項式になっている.このことをまとめると次のようになる.
定理1の状況で,任意の$l=1,\dots,n$について多項式
$$
q_1 + \sum_{k=1}^{l-1} A_k(x-p_1)\cdots (x-p_k)
$$
が点$P_1,\dots,P_l$に関する補間多項式となるような実数$A_1,\dots,A_{n-1}$が存在する.
あとは$A_1,\dots,A_{n-1}$が$P_1,\dots,P_n$を用いて具体的に書ければよい.差商はこの簡便な表記を与える.
定理1の状況で,差商$[q_1, \dots, q_n]$を次のように定義する.
\begin{align} &[q_1] = q_1\\ &[q_1,\dots,q_k] = \frac{[q_1,\dots,q_{k-1}]-[q_2,\dots,q_k]}{p_1-p_k} \quad (k \geqq 2) \end{align}
関数$g(x)$が$q_1=f(p_1),\dots,q_n=f(p_n)$を満たす場合,$[q_1,\dots,q_n]$を$g[p_1,\dots,p_n]$とも表記する.
$(p_1,q_1)=(1,6),(p_2,q_2)=(5,2),(p_3,q_3)=(4,3)$のとき
$$
[q_1, q_2] = \frac{6-2}{1-5} = -1,\,
[q_2, q_3] = \frac{2-3}{5-4} = -1,\,
[q_1,q_2,q_3] = \frac{-1-(-1)}{1-4} = 0
$$
である.
定理1の状況で,$f(x)$は次のように表せる.
$$
f(x) = q_1 + \sum_{k=1}^{n-1} [q_1,\dots,q_{k+1}] (x-p_1) \cdots (x-p_k)
$$
帰納法により示す.$n=1$のときは$f(x)=q_1$なので明らかに成り立つ.次に,$n-1$個以下の点に関する補間多項式について成立を仮定する.点$P_1,\dots,P_n$に関する補間多項式を$f(x)$とする.点$P_1, \dots, P_{n-1}$に関する補間多項式を$g(x)$,$P_2, \dots, P_n$に関する補間多項式を$h(x)$とおくと,多項式
$$
\frac{(x-p_1)h(x) - (x-p_n)g(x)}{p_n-p_1}
$$
は次数が$n-1$以下であり,かつ点$P_1,\dots,P_n$を通る.定理1により補間多項式は一意なので,これは補間多項式$f(x)$である.右辺の$n-1$次の項の係数($0$であることもある)は,帰納法の仮定により
$$
\frac{[q_2,\dots,q_n]-[q_1,\dots,q_{n-1}]}{p_n-p_1} = [q_1,\dots,q_n]
$$
である.定理2により,$f(x)$は実数$A_1,\dots,A_{n-1}$によって
$$
f(x) = q_1 + \sum_{k=1}^{n-1} A_k(x-p_1)\cdots (x-p_k)
$$
と書けるが,この$n-1$次の項の係数は$A_{n-1}$であるので
$$
f(x) = \pqty{q_1 + \sum_{k=1}^{n-2} A_k(x-p_1)\cdots (x-p_k)} + [q_1,\dots,q_n](x-p_1)\cdots (x-p_{n-1})
$$
である.上の第1項は$g(x)$に等しいので,帰納法の仮定により
\begin{align*}
f(x)
&= \pqty{q_1 + \sum_{k=1}^{n-2} [q_1,\dots,q_{k+1}](x-p_1)\cdots (x-p_k)} + [q_1,\dots,q_n](x-p_1)\cdots (x-p_{n-1}) \\
&= q_1 + \sum_{k=1}^{n-1} [q_1,\dots,q_{k+1}](x-p_1)\cdots (x-p_k)
\end{align*}
である.よって,$n$個の点に関する補間多項式についても命題は成り立つ.
このように,多項式$(x-p_1) \dots (x-p_k)\,(k=1,\dots,n-1)$の定数倍の和によって,点$P_1,\dots,P_n$に関する補間多項式を得る方法をニュートン補間という.
例3により,点$(1,6),(5,2),(4,3)$に関する補間多項式は
$$
6+(-1)(x-1)+0(x-1)(x-5) = -x+7
$$
である.定理1からも分かるように,これは例2と一致している.
補間多項式による近似の誤差
補間多項式はしばしば,関数を近似するために用いられる.この節では,補間多項式による近似がどの程度妥当であるか分析する方法について考察する.
$n$は$2$以上の整数とする.$f(x)$を関数とし,曲線$y=f(x)$上の点$P_1=(x_1, f(x_1)),\dots,P_n=(x_n, f(x_n))$は$x_1<\dots< x_n$を満たすとする.点$P_1,\dots,P_n$に関する補間多項式を$p(x)$とおくと,$f(x)$が十分に滑らかであれば,$x$が$x_1,\dots,x_n$に近いとき$f(x)$の値と$p(x)$の値はごく近いことが期待できる.次の定理はこのことを保証するものである.
上の状況で,関数$f(x)$は$n$階微分可能であるとする.このとき,任意の$t\in (x_1,x_n)$に対し
$$
f(t)-p(t) = \frac{f^{(n)} (\xi)}{n!} (t-x_1)\cdots (t-x_n)
$$
を満たす$\xi \in (x_1, x_n)$が存在する.これにより,$\abs{f^{(n)}(x)}$が区間$[x_1, x_n]$で最大値を持てば
$$
\abs{f(t)-p(t)}
\leqq \max_{x_1\leqq\xi\leqq x_n} \frac{\abs{f^{(n)}(\xi)}}{n!} \abs{(t-x_1)\cdots (t-x_n)}
\leqq \max_{x_1\leqq\xi\leqq x_n} \frac{\abs{f^{(n)}(\xi)}}{n!} (x_n-x_1)^n
$$
である.
この定理は次の補題から導かれる.
閉区間$I=[a,b]$で定義された関数$g(x)$は$I$における$n+1$個の点で$0$であり,かつ$I$で$n$階微分可能であるとする.このとき$g^{(n)}(\xi) = 0$を満たす$\xi \in (a,b)$が存在する.
どの2つも相異なる$n+1$個の実数$x_1,\dots,x_{n+1} \in I$について$g(x_1) = \cdots = g(x_{n+1}) =0$であるとする.$j=1,\dots,n$に対し,$I_{1,j}=[x_j,x_{j+1}], \mathring{I}_{1,j}=(x_j,x_{j+1})$とおく.関数$g(x)$は$I_{1,j}$で連続かつ$\mathring{I}_{1,j}$で微分可能なので,平均値の定理により
$$
g^{(1)}(\xi_{1j}) = \frac{g(x_j)-g(x_{j+1})}{x_j-x_{j+1}} = \frac{0-0}{x_j-x_{j+1}}=0
$$
を満たす$\xi_{1,j} \in \mathring{I}_{1,j}$が存在する.これにより,$n$個の実数$\xi_{1,1} < \dots < \xi_{1,n}$を$g^{(1)}(x)$の値が$0$であるように取れる.この$n$項数列を$\xi_1 = \{ \xi_{1,n} \}$とする.
同様に,$j=1,\dots,n-1$に対して,$I_{2,j}=[\xi_{1,j},\xi_{1,j+1}], \mathring{I}_{2,j}=(\xi_{1,j},\xi_{1,j+1})$とおく.再び平均値の定理により
$$
g^{(2)}(\xi_{2,j}) = \frac{g^{(1)}(\xi_{1,j})-g^{(1)}(\xi_{1,j+1})}{\xi_{1,j}-\xi_{1,j+1}} = \frac{0-0}{\xi_{1,j}-\xi_{1,j+1}} = 0
$$
を満たす$\xi_{2,j} \in \mathring{I}_{2,j}$が存在する.$\xi_{2,1},\dots,\xi_{2,n-1}$により,さきほどと同様に$n-1$項数列$\xi_2 = \{ \xi_{2,n} \}$を定義する.
以下,これを繰り返すことによって数列$\xi_3,\dots,\xi_n$を定義する.$\xi_j$は$n+1-j$項数列であり,その項に現れる任意の数$a$は$g^{(j)}(a)=0$を満たす.よって,特に$j=n$のとき$\xi_n$は項をただ1つもち,その項$\xi$は$g^{(n)}(\xi)=0$を満たす.
以上の補題により,定理4は次のように証明される.
$t=x_2,\dots,x_{n-1}$のときは$(t-x_1)\cdots (t-x_n)=0$であるから,$\xi$は区間$(x_1,x_n)$上の任意の値にしてよい(たとえば$\xi=(x_1+x_n)/2$とすればよい).そこで,$t$が$x_2,\dots,x_{n-1}$のいずれとも等しくない場合について示す.
$$
g(x) = f(x)-p(x)-a(x-x_1)\cdots (x-x_n)
$$
とおく.ただし$a$は$g(t)=0$であるように取る.すなわち
$$
a = \frac{f(t)-p(t)}{(t-x_1)\cdots (t-x_n)}
$$
とする.
$x=x_1,\dots,x_n,t$のとき$g(x)=0$であり,かつ関数$g(x)$は仮定により$n$階微分可能である.よって,補題5により$g^{(n)}(\xi)=0$を満たす$\xi\in (x_1,x_n)$が存在する.ここで
$$
g^{(n)}(\xi) = f^{(n)}(\xi)-p^{(n)}(\xi)-an! = 0\quad\therefore\, a = \frac{f^{(n)}(\xi)-p^{(n)}(\xi)}{n!}
$$
である.$p(x)$の次数は最大でも$n-1$なので$p^{(n)}(\xi)=0$であり
$$
a = \frac{f^{(n)}(\xi)}{n!}
\quad\therefore\, f(t)-p(t)-\frac{f^{(n)}(\xi)}{n!}(t-x_1)\cdots (t-x_n) = g(t) = 0
$$
となる.したがって
$$
f(t)-p(t) = \frac{f^{(n)}(\xi)}{n!}(t-x_1)\cdots (t-x_n)
$$
である.後半は明らか.
$\sin \degree{10.5}$の近似値を求めよう.数表により,近似値
$$
\sin \degree{10}=0.1736,\quad \sin \degree{11}=0.1908,\quad \sin \degree{12}=0.2079
$$
が分かっているとする.このとき,点$(10,0.1736),(11,0.1908),(12,0.2079)$に関する補間多項式は$p(x) = -0.00005 x^2 + 0.01825x - 0.0039$である.よって
$$
\sin \degree{10.5} \fallingdotseq p(10.5) = 0.182213
$$
となる.
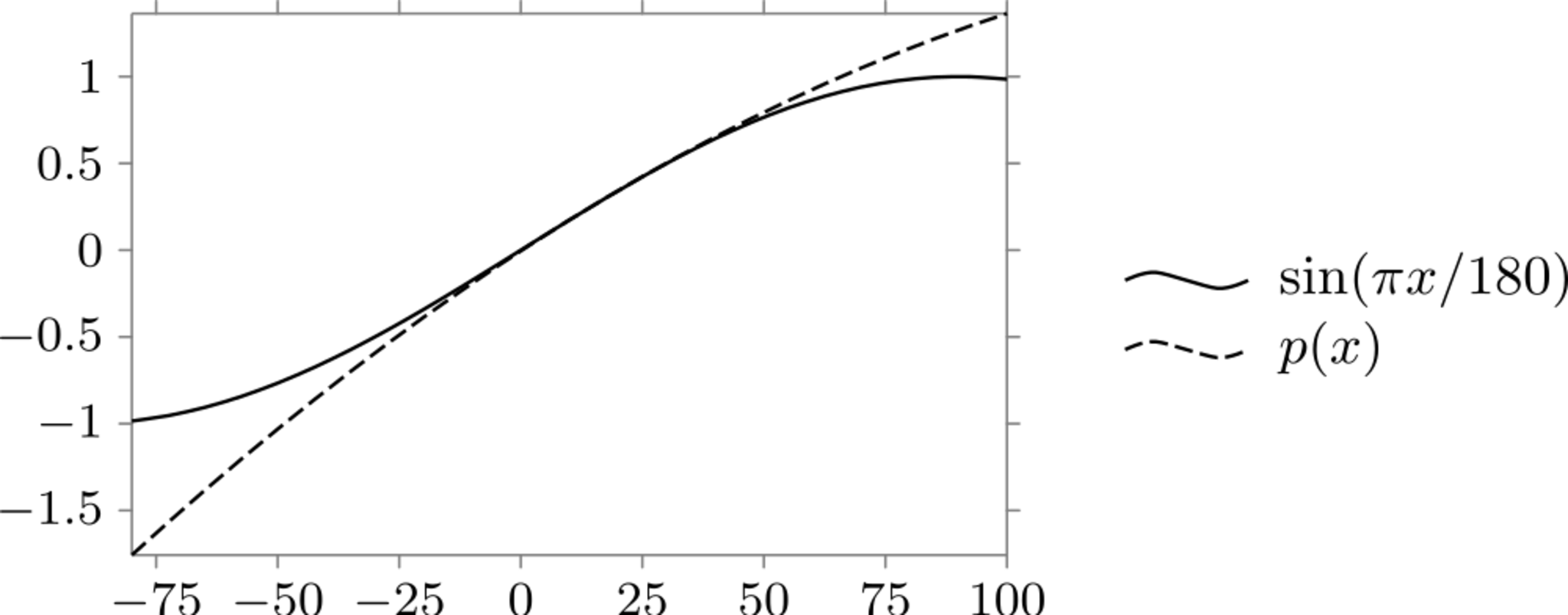 sin(πx/180)とp(x)の比較
sin(πx/180)とp(x)の比較
この近似の妥当性を考える.定理4,および
$$
\abs{\frac{\mathrm{d}^3}{\mathrm{d}x^3} \sin\pqty{\frac{\pi}{180} x}} = \abs{\pqty{\frac{\pi}{180}}^3\cos\pqty{\frac{\pi}{180} x}} \leqq \pqty{\frac{\pi}{180}}^3
$$
により
$$
\abs{\sin \degree{10.5} - p(10.5)} \leqq \pqty{\frac{\pi}{180}}^3 \frac{1}{3!} \abs{(12-10)}^3 \fallingdotseq 7.08\times 10^{-6}
$$
である.これは利用した近似値の有効数字である$4$桁よりも十分に小さいので,$\sin \degree{10.5} = 0.1822$は有効数字$4$桁で正しいと考えられる.実際,$\sin \degree{10.5} = 0.182236\dots$なので,確かに有効数字$4$桁で正しい値が得られている.また,有効数字$4$桁の数表に基づく限り,補間多項式の次数をこれ以上増やす必要は無いことも分かる.
