高校数学から始める数値計算（２）：数値微分・数値積分
目次
本稿は「3. 数値微分」と「4. 数値積分」に当たります．なお，本稿はこの PDF版 を元に，Mathlogの仕様に合わせて一部の文言・体裁を変更したものです．内容は変わりません．
数値微分
関数を補間多項式で近似できるのなら，ある点における微分係数もまた，補間多項式の微分係数で近似できると考えられる．すなわち，実数$x_1,\dots,x_n$はどの２つも相異なり，$t$が$x_1,\dots,x_n$に十分近いとき，点$(x_1,f(x_1)),\dots,(x_n,f(x_n))$に関する補間多項式を$p(x)$とすると$f'(t) \fallingdotseq p'(t)$であると考えられる．
このような微分の近似を数値微分という．数値微分をするときは$x_1,\dots,x_n$を等間隔に取ることが多い．以下にこの場合の例を示す．
$n=2$かつ$(x_1,x_2)=(t,t+h)$のとき
$$
p(x) = f(t) + f[t,t+h](x-t)
$$
である．よって
$$
f'(t) \fallingdotseq {\dv{p}{x}}(t) = f[t,t+h] = \frac{f(t+h)-f(t)}{h}
$$
である．$h\to 0$においては，この式の右辺は厳密に$f'(t)$と等しくなる．
$n=3$かつ$(x_1,x_2,x_3)=(t-h,t,t+h)$のとき
$$
p(x) = f(t-h) + f[t-h,t]\pqty{x-(t-h)} + f[t-h,t,t+h]\pqty{x-(t-h)}(x-t)
$$
である．よって
\begin{gather*}
{\dv{p}{x}}(x) = f[t-h,t] + f[t-h,t,t+h](2x-2t+h) \\
f'(t) \fallingdotseq \frac{f(t)-f(t-h)}{h} + \frac{h^{-1}\pqty{f(t)-f(t-h)}-h^{-1}\pqty{f(t+h)-f(t)}}{(t-h)-(t+h)}h
= \frac{f(t+h)-f(t-h)}{2h}
\end{gather*}
である．この式についても，$h\to 0$においては
$$
\frac{f(t+h)-f(t-h)}{2h} = \frac{f(t+h)-f(t)}{2h} + \frac{f(t)-f(t-h)}{2h} \to \frac{f'(t)}{2} + \frac{f'(t)}{2} = f'(t)\quad (h\to 0)
$$
が成立する．
数値微分の比較
図は，２つの直線
\begin{align*}
l_1 &\colon\, y = \frac{f(t+h)-f(t)}{h} (x - t) + f(t) \\
l_2 &\colon\, y = \frac{f(t+h)-f(t-h)}{(t+h)-(t-h)} (x - (t-h)) + f(t-h)
\end{align*}
を$f(x)=\sin(x), t=\pi/3, h=0.2$の場合について示したものである．図によれば，$l_2$は$l_1$よりも傾きが$1/2 = \cos(\pi/3)$に近い．したがって，$(\sin(x))'$の$x=\pi/3$における近似に関しては，例1よりも例2のほうが真値に近い値を与えている．より一般に，$h$を変えない場合，高次の補間多項式を利用した公式ほど近似値は真値に近づく傾向にある．
ニュートン・コーツの公式
関数$f(x)$の区間$I = [a, b]\,(a< b)$における定積分を考える．実数$x_1,\dots,x_n \in I$は$a \leqq x_1 < \dots < x_n \leqq b$を満たすとし，点$(x_1,f(x_1)),\dots,(x_n,f(x_n))$に関する補間多項式を$p(x)$とおく．このとき，$p(x)$で$f(x)$がよく近似できていれば
$$
\int_a^b f(x) \dd{x} \fallingdotseq \int_a^b p(x) \dd{x}
$$
となることが期待できる．
右辺について，
補間多項式の公式
を利用すると
$$
\int_a^b p(x) \dd{x}
= \int_a^b \pqty{\sum_{i=1}^n f(x_i) \prod_{k\neq i} \frac{x - x_k}{x_i - x_k}} \dd{x}
= \sum_{i=1}^n f(x_i) \int_a^b \prod_{k\neq i} \frac{x - x_k}{x_i - x_k} \dd{x}
$$
である．よって
$$
w_i = \int_a^b \prod_{k\neq i} \frac{x - x_k}{x_i - x_k} \dd{x} \quad (i=1,\dots,n)
$$
とおくと，冒頭の近似式は
$$
\int_a^b f(x) \dd{x} \fallingdotseq \sum_{i=1}^n w_i f(x_i)
$$
という形に書ける．
点$x_1,\dots,x_n$のことを標本点，実数$w_1,\dots,w_n$のことを重みという．上の式から，重み$w_1,\dots,w_n$は積分区間$I$と標本点$x_1,\dots,x_n$の取り方のみに依存し，関数$f(x)$によらないことが分かる．
特にここで，実数$x_1,\dots,x_n$を区間$[a,b]$上で均等に取り
$$
x_i = a + (b-a)\frac{i-1}{n-1} \quad (i = 1,\dots,n)
$$
として定積分を近似する方法を閉じたニュートン・コーツの公式という（注：端点を含めず，$x_i = a + (b-a)i/(n+1)$とする方法を開いたニュートン・コーツの公式という．性質は閉じたニュートン・コーツの公式とほとんど同様である）．
閉じたニュートン・コーツの公式の誤差は，
補間多項式による近似の誤差
の不等式を両辺ともに積分することで評価できる．実際
\begin{align*}
\abs{\int_a^b f(x) \dd{x} - \int_a^b p(x) \dd{x}}
&\leqq \int_a^b \abs{f(x) - p(x)} \dd{x} \\
&\leqq (b-a)\max_{a\leqq t\leqq b} \abs{f(t) - p(t)} \\
&\leqq (b-a)\pqty{\max_{a\leqq\xi\leqq b} \frac{\abs{f^{(n)}(\xi)}}{n!} (b-a)^n} \\
&= \max_{a\leqq\xi\leqq b} \frac{\abs{f^{(n)}(\xi)}}{n!} (b-a)^{n+1}
\end{align*}
である（ただし，この評価は最良ではない．ニュートン・コーツの公式に関しては，より良い評価方法が知られている）．
以下では$n=2,3$について，$w_1,\dots,w_n$を計算し誤差を見積もる．
$n=2$のとき
\begin{align*}
w_1
&= \int_a^b \frac{x-x_2}{x_1-x_2} \dd{x}
= \int_a^b \frac{x-b}{a-b} \dd{x}
= \frac{b-a}{2} \\
w_2
&= \int_a^b \frac{x-x_1}{x_2-x_1} \dd{x}
= \int_a^b \frac{x-a}{b-a} \dd{x}
= \frac{b-a}{2}
\end{align*}
である．つまり，$n=2$のときの閉じたニュートン・コーツの公式は
$$
\int_a^b f(x) \dd{x} \fallingdotseq \frac{b-a}{2} \pqty{f(a)+f(b)}
$$
と表される．この公式を台計則という．台計則の誤差は
$$
\abs{\int_a^b f(x) \dd{x} - \int_a^b p(x) \dd{x}}
\leqq \max_{a\leqq\xi\leqq b} \frac{\abs{f^{(2)}(\xi)}}{2} (b-a)^3
$$
と評価できる．なお，台計則は２点$(a,f(a)),(b,f(b))$に関する補間多項式を利用しているので，$1$次以下の多項式関数に関しては（
補間多項式の一意性
により）厳密な値を与える．
なお，本稿では示さないが，もう少し厳しく
$$
\abs{\int_a^b f(x) \dd{x} - \int_a^b p(x) \dd{x}} \leqq \max_{a\leqq\xi\leqq b} \frac{\abs{f^{(2)}(\xi)}}{12} (b-a)^3
$$
と評価できることが知られている[3]．
$n=3$のとき
\begin{align*}
w_1
&= \int_a^b \frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} \dd{x}
= \int_a^b \frac{\pqty{x-2^{-1}(a+b)}(x-b)}{\pqty{a-2^{-1}(a+b)}(a-b)} \dd{x}
= \frac{b-a}{6} \\
w_2
&= \int_a^b \frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)} \dd{x}
= \int_a^b \frac{(x-a)(x-b)}{\pqty{2^{-1}(a+b)-a}\pqty{2^{-1}(a+b)-b}} \dd{x}
= \frac{2(b-a)}{3} \\
w_3
&= \int_a^b \frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} \dd{x}
= \int_a^b \frac{(x-a)(x-2^{-1}(a+b))}{(b-a)(b-2^{-1}(a+b))} \dd{x}
= \frac{b-a}{6}
\end{align*}
である．つまり，$n=3$のときの閉じたニュートン・コーツの公式は
$$
\int_a^b f(x) \dd{x} \fallingdotseq \frac{b-a}{6}\pqty{f(a) + 4f\pqty{\frac{a+b}{2}} + f(b)}
$$
と表される．この公式をシンプソン則という．シンプソン則の誤差は
$$
\abs{\int_a^b f(x) \dd{x} - \int_a^b p(x) \dd{x}}
\leqq \max_{a\leqq\xi\leqq b} \frac{\abs{f^{(3)}(\xi)}}{6} (b-a)^4
$$
と評価できる．
台計則と同様に考えれば，シンプソン則は$2$次以下の多項式関数について厳密な値を与えることが分かる．ところが，シンプソン則はさらに性質が良い．$f(x)=x^3$のときを考えると，このとき
$$
\frac{b-a}{6}\pqty{f(a) + 4f\pqty{\frac{a+b}{2}} + f(b)}
= \frac{b-a}{6}\pqty{a^3 + 4\pqty{\frac{a+b}{2}}^3 + b^3}
= \frac{b^4-a^4}{4}
= \int_a^b f(x) \dd{x}
$$
である．つまり，シンプソン則は$3$次多項式関数についても厳密な値を与える．
実は，シンプソン則の誤差は
$$
\abs{\int_a^b f(x) \dd{x} - \int_a^b p(x) \dd{x}} \leqq \max_{a\leqq\xi\leqq b} \frac{\abs{f^{(4)}(\xi)}}{2880} (b-a)^5
$$
と評価できることが知られている[3]．この式からも，シンプソン則が$3$次以下の多項式関数について厳密な値を与えることが分かる．
台形則とシンプソン則
図は，定積分$\displaystyle \int_{-3}^1 e^x \dd{x}$の台形則とシンプソン則による近似で利用される補間多項式を示したものである．この場合，シンプソン則では$e^x$の下側を通る部分と上側を通る部分がちょうど相殺され，より真値に近い値が得られると期待できる．実際，この真値は
$$
\int_{-3}^1 e^x \dd{x} = 2.6685\dots
$$
であり，台形則とシンプソン則による近似値はそれぞれ
\begin{align*}
\frac{1-(-3)}{2} \pqty{e^{-3}+e^1} &= 5.5361\dots \\
\frac{1-(-3)}{6} \pqty{e^{-3} + 4e^{-1} + e^1} &= 2.8263\dots
\end{align*}
である．
閉じたニュートン・コーツの公式はたいてい，積分区間を複数の小区間に区切ってから，その各区間に対して適用される．この場合，台計則は複合台計則，シンプソン則は複合シンプソン則と呼ばれる（単に台形則，シンプソン則とも呼ばれる）．例で見たように，閉じたニュートン・コーツの公式の誤差は$b-a$に依存する．したがって，複合台形公式と複合シンプソン則の誤差は，$b-a$を小さく取るほど，すなわち，区間を多く分割するほど改良されると考えられる．
ガウス・ルジャンドル公式
ニュートン・コーツの公式では標本点を均等に取って定積分を近似した．この節では，標本点の取り方を工夫することで，ニュートン・コーツの公式と比べて少ない標本点で良い近似を得る方法を示す．
正の整数$n$に対し
$$
L_n(x) = \frac{1}{2^n n!} \ndv{n}{x} \bqty{(x^2 -1)^n}
$$
で定義される多項式を$n$次のルジャンドル多項式という（注：正確には，この式における$\mathrm{d}/\mathrm{d}x$は形式微分である．本稿では普通の微分と特に区別せず扱う）．
\begin{align*}
L_1(x) &= \frac{1}{2} \cdot 2x = x
& L_2(x) &= \frac{1}{8} (12x^2-4) = \frac{1}{2} (3x^2 - 1) & \\
L_3(x) &= \frac{1}{48} (120 x^3 - 72x) = \frac{1}{2} (5x^3 - 3x)
& L_4(x) &= \frac{1}{8} (63x^5-70x^3+15x)
\end{align*}
である．
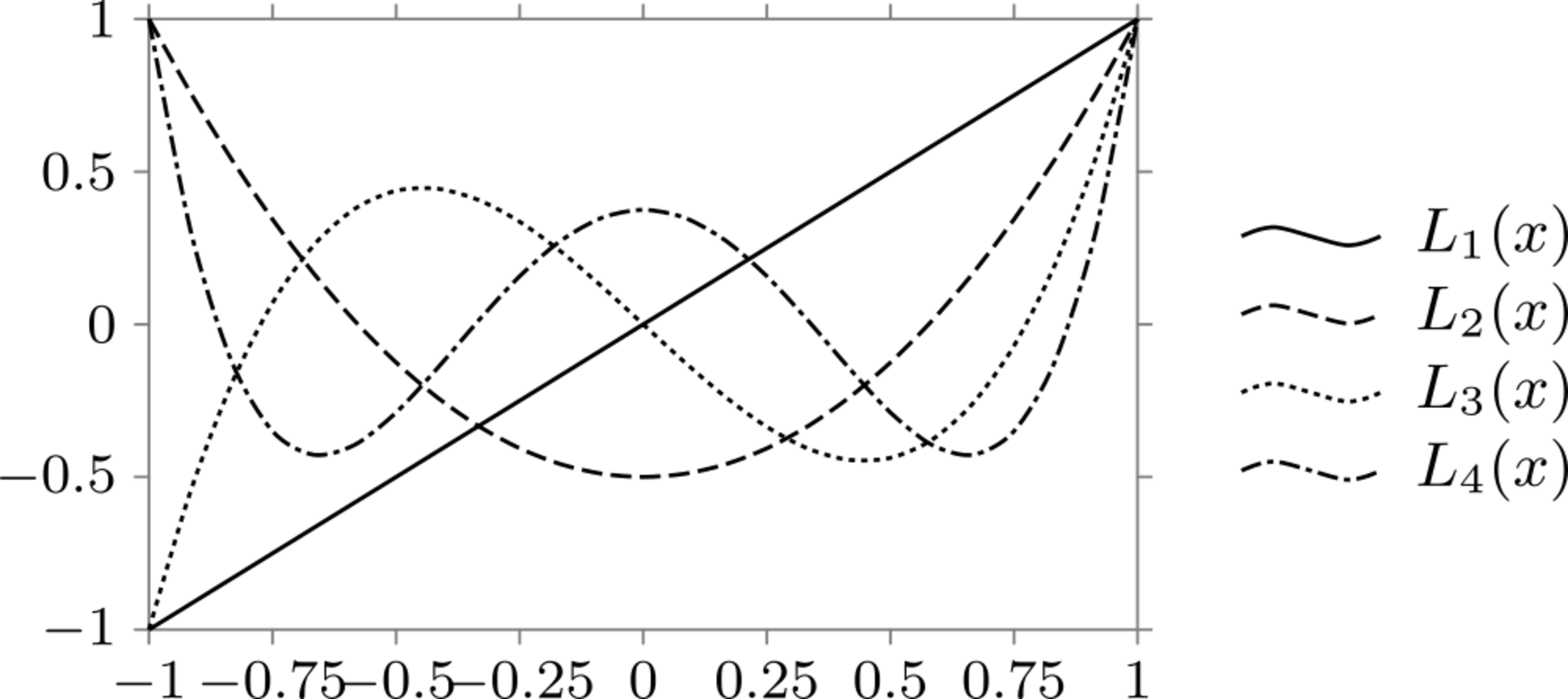ルジャンドル多項式
$L_n(x)$は区間$\mathring{I} = (-1,1)$に$n$個の相異なる根を持つ．
なお，多項式$f(x)$の根とは$f(\alpha)=0$を満たす値$\alpha$のことである．この定理を示す前に，次の補題を示す．
関数$f(x), g(x)$は$n$階微分可能とする．このとき，正の整数$n$に対して
$$
\ndv{n}{x} \pqty{f(x)g(x)} = \sum_{k=0}^n \binom{n}{k} f^{(k)}(x) g^{(n-k)}(x)
$$
である．ただし$\binom{n}{k}$は二項係数である．
帰納法により示す．$n=1$のとき，積の微分法則により
$$
\dv{}{x} \pqty{f(x)g(x)} = f(x)g'(x) + f'(x)g(x)
$$
であり成り立つ．また，ある$n$での成立を仮定すると
\begin{align*}
\ndv{n+1}{x} \pqty{f(x)g(x)}
&= \dv{}{x} \pqty{\ndv{n}{x} f(x)g(x)} \\
&= \dv{}{x} \sum_{k=0}^n \binom{n}{k} f^{(k)}(x) g^{(n-k)}(x) \\
&= \sum_{k=0}^n \binom{n}{k} \pqty{f^{(k)}(x) g^{(n-k+1)}(x) + f^{(k+1)}(x) g^{(n-k)}(x)} \\
&= \sum_{k=0}^{n} \binom{n}{k} f^{(k)}(x) g^{(n+1-k)}(x) + \sum_{k=1}^{n+1} \binom{n}{k-1} f^{((k-1)+1)}(x) g^{(n-(k-1))}(x) \\
&= f(x)g^{(n+1)}(x) + \pqty{\sum_{k=1}^{n} \pqty{\binom{n}{k} + \binom{n}{k-1}} f^{(k)}(x) g^{(n+1-k)}(x)} + f^{(n+1)}(x)g(x) \\
&= \sum_{k=0}^{n+1} \binom{n+1}{k} f^{(k)}(x) g^{(n+1-k)}(x) \quad \pqty{\because\, \binom{n}{k} + \binom{n}{k-1} = \binom{n+1}{k}}
\end{align*}
となり，成立が確かめられる．
補題2により，定理1は以下のように証明できる．
$x^n$を$k$階微分したときの係数を$A_k$とする．
$$
f(x) = \pqty{x^2-1}^n = (x-1)^n (x+1)^n
$$
とおく．補題1により，$l=1,\dots,n-1$について
\begin{align*}
f^{(l)}(x)
&= \sum_{k=0}^l \binom{l}{k} \pqty{\ndv{k}{x} (x-1)^n} \pqty{\ndv{l-k}{x} (x+1)^n} \\
&= \sum_{k=0}^l \binom{l}{k} A_{k} (x-1)^{n-k} A_{l-k} (x+1)^{n-(l-k)} \\
&= (x-1)^{n-l} (x+1)^{n-l} \sum_{k=0}^l \binom{l}{k} A_{k} A_{l-k} (x-1)^{l-k} (x+1)^k
\end{align*}
である．よって，$f^{(1)}(x),\dots,f^{(n-1)}(x)$の$x=-1,1$における値は$0$である．
このことを用い，$l=1,\dots,n$について$f^{(l)}(x)$が区間$\mathring{I}$上に$l$個の相異なる根を持つことを示す．まず，$l=1$のときは平均値の定理により
$$
f'(\xi) = \frac{f(1)-f(-1)}{1-(-1)} = \frac{0-0}{1-(-1)}=0
$$
を満たす$\xi \in \mathring{I}$が存在する．
次に，ある$l< n$での成立を仮定する．すなわち，$l$個の実数$\xi_1, \dots, \xi_l \in \mathring{I}$（ただし$\xi_1 < \cdots < \xi_l$とする）が存在して，$f^{(l)}(\xi_1) = \cdots = f^{(l)}(\xi_l) = 0$を満たすとする．このとき，$\xi_0 = -1, \xi_{l+1} = 1$とおくと，平均値の定理により$k=0,\dots,l$に対し
$$
f^{(l+1)}(\xi'_k) = \frac{f^{(l)}(\xi_k) - f^{(l)}(\xi_{k+1})}{\xi_k - \xi_{k+1}} = \frac{0 - 0}{\xi_k - \xi_{k+1}} = 0
$$
を満たす$\xi'_k \in (\xi_k, \xi_{k+1}) \subset \mathring{I}$が存在する．よって，$f^{(l+1)}(x)$もまた$l+1$個の相異なる根を$\mathring{I}$上に持つ．
以上により，帰納的に$f^{(n)}(x)$は$\mathring{I}$上に$n$個の相異なる根を持つ．$2^n n! L_n(x) = f^{(n)}(x)$なので，$L_n(x)$もまた$\mathring{I}$上に$n$個の相異なる根を持つ．
$k = 1,\dots,n-1$なら
$$
\int_{-1}^1 x^k L_n(x) \dd{x} = 0
$$
である．
定理1の証明と同様に
$$
f(x) = \pqty{x^2-1}^n = (x-1)^n (x+1)^n
$$
とおく．このとき
$$
\int_{-1}^1 x^k L_n(x) \dd{x}
= \int_{-1}^1 x^k \frac{1}{2^n n!} f^{(n)}(x) \dd{x}
= \frac{1}{2^n n!} \int_{-1}^1 x^k f^{(n)}(x) \dd{x}
$$
である．部分積分により
$$
\int_{-1}^1 x^k f^{(n)}(x) \dd{x}
= \bqty{x^k f^{(n-1)}(x)}_{-1}^1 - \int_{-1}^1 kx^{k-1} f^{(n-1)}(x) \dd{x}
$$
であるが，定理1の証明で見たように，$l=1,\dots,n-1$に対して
$$
f^{(l)}(-1) = f^{(l)}(1) = 0
$$
なので
$$
\int_{-1}^1 x^k f^{(n)}(x) \dd{x}
= -k\int_{-1}^1 x^{k-1} f^{(n-1)}(x) \dd{x}
$$
である．同様に部分積分を繰り返すことで
$$
\abs{\int_{-1}^1 x^k f^{(n)}(x) \dd{x}}
= \abs{\int_{-1}^1 k! x^0 f^{(n-k)}(x) \dd{x}}
= k! \abs{f^{(n-k-1)}(1) - f^{(n-k-1)}(-1)}
= 0
$$
が得られる．よって
$$
\int_{-1}^1 x^k L_n(x) \dd{x}
= \frac{1}{2^n n!} \int_{-1}^1 x^k f^{(n)}(x) \dd{x}
= 0
$$
である．
以上により，次の定理がしたがう．
$\mathring{I} = (-1,1)$とし，$x_1,\dots,x_n$を$\mathring{I}$上にある$L_n(x)$の相異なる$n$個の根とする．このとき，$f(x)$が$2n-1$次以下の多項式関数であれば，点$(x_1,f(x_1)),\dots,(x_n,f(x_n))$に関する補間多項式$p(x)$は
$$
\int_{-1}^1 f(x) \dd{x} = \int_{-1}^1 p(x) \dd{x}
$$
を満たす．言い換えると，重み$w_1,\dots,w_n$を
$$
w_i = \int_a^b \prod_{k\neq i} \frac{x - x_k}{x_i - x_k} \dd{x}
\quad (i = 1,\dots,n)
$$
で定めると
$$
\int_{-1}^1 f(x) \dd{x} = \sum_{i=1}^n w_i f(x_i)
$$
が成り立つ．
$L_n(x)$の相異なる$n$個の根を$x_1,\dots,x_n$とおく．関数$f(x)$に対し
$$
G[f(x)] = \sum_{i=1}^n w_i f(x_i) \quad
\pqty{w_i = \int_a^b \prod_{k\neq i} \frac{x - x_k}{x_i - x_k} \dd{x}}
$$
とする．ニュートン・コーツの公式で見たように，$G[f(x)]$は点$(x_1,f(x_1)),\dots,(x_n,f(x_n))$に関する補間多項式を区間$[-1, 1]$で定積分した値である．
$G[\cdot]$の定義により，$I$で定義される任意の関数$f(x), g(x)$に関して
$$
G[f(x) + g(x)] = G[f(x)] + G[g(x)]
$$
が成立する．
$f(x)$を$2n-1$次以下の多項式関数とすると，$f(x)$は（多項式の意味で）$L_n(x)$により割れる．商を$q(x)$，余りを$r(x)$とすると
$$
f(x) = q(x)L_n(x) + r(x)
$$
となる．したがって
$$
G[f(x)] = G[q(x)L_n(x)] + G[r(x)]
$$
であるが，$x_1,\dots,x_n$は$L_n(x)$の根であるから
$$
G[q(x)L_n(x)]
= \sum_{k=1}^n w_k q(x_k) L_n(x_k)
= \sum_{k=1}^n w_k q(x_k) \cdot 0
= 0
$$
である．したがって$G[f(x)] = G[r(x)]$である．$r(x)$の次数は$L_n(x)$の次数を超えないので，$r(x)$の次数は最大でも$n-1$である．よって，
補間多項式の一意性
により点$(x_1,r(x_1)),\dots,(x_n,r(x_n))$に関する補間多項式は$r(x)$に一致する．すなわち
$$
G[f(x)] = G[r(x)] = \int_{-1}^1 r(x) \dd{x}
$$
である．
一方，$q(x)$の次数は$n-1$以下なので，定理3により
$$
\int_{-1}^1 f(x) \dd{x}
= \int_{-1}^1 q(x)L_n(x) \dd{x} + \int_{-1}^1 r(x) \dd{x}
= \int_{-1}^1 r(x) \dd{x}
$$
である．よって
$$
G[f(x)] = \int_{-1}^1 r(x) \dd{x} = \int_{-1}^1 f(x) \dd{x}
$$
が成り立つ．
定理4により，関数$f(x)$が$2n-1$次以下の多項式関数でよく近似できるときは，標本点をルジャンドル多項式$L_n(x)$の$n$個の根にすることで，より正確な近似値が得られると考えられる．この方法をガウス・ルジャンドル公式という．
定積分$\displaystyle \int_{-3}^1 e^x \dd{x}$をガウス・ルジャンドル公式によって近似する．
定積分$\displaystyle \int_{-3}^1 e^x \dd{x}$は積分区間が$[-1, 1]$でない．そこで，置換積分により変数を
$$
t = \frac{x+1}{2},\, \dd{x} = 2\dd{t}
$$
に変え$\displaystyle \int_{-1}^1 2e^{2t-1} \dd{t}$を計算する．$L_3(x)$の根$x_1,x_2,x_3\,(x_1< x_2< x_3)$は，方程式$L_3(x)=0$を解くことで
$$
\frac{1}{2} (5x^3 - 3x) = 0 \quad\therefore\,
x_1 = -\sqrt{\frac{3}{5}}, x_2 = 0, x_3 = \sqrt{\frac{3}{5}}
$$
と分かる．$x_1,x_2,x_3$に対応する重みはそれぞれ
$$
w_1 = \frac{5}{9}, w_2 = \frac{8}{9}, w_3 = \frac{5}{9}
$$
である．したがって，ガウス・ルジャンドル公式によれば$f(x)=2e^{2x-1}$とすると
$$
\int_{-1}^1 2e^{2t-1} \dd{t}
\fallingdotseq \frac{5}{9}f\pqty{-\sqrt{\frac{3}{5}}} + \frac{8}{9}f\pqty{0} + \frac{5}{9}f\pqty{\sqrt{\frac{3}{5}}}
= 2.6651\dots
$$
である．これは例5で見たシンプソン則による近似値$2.8263\dots$よりも真値$2.6685\dots$に近い．
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
