高校数学から始める数値計算（３）：ルンゲ現象・補間多項式とテイラー多項式の関係
目次
本稿は「5. 補遺」に当たります．なお，本稿はこの PDF版 を元に，Mathlogの仕様に合わせて一部の文言・体裁を変更したものです．内容は変わりません．
ルンゲ現象
定理1.4
の状況で，$f(x)=(25x^2+1)^{-1}$のときを考える．
$$
x_i = -1 + 2\frac{i-1}{n-1} \quad (i=1,\dots,n)
$$
とおき，$p_n(x)$を点$(x_1, f(x_1)),\dots,(x_n,f(x_n))$に関する補間多項式としたとき，その様子は下図のようになる．
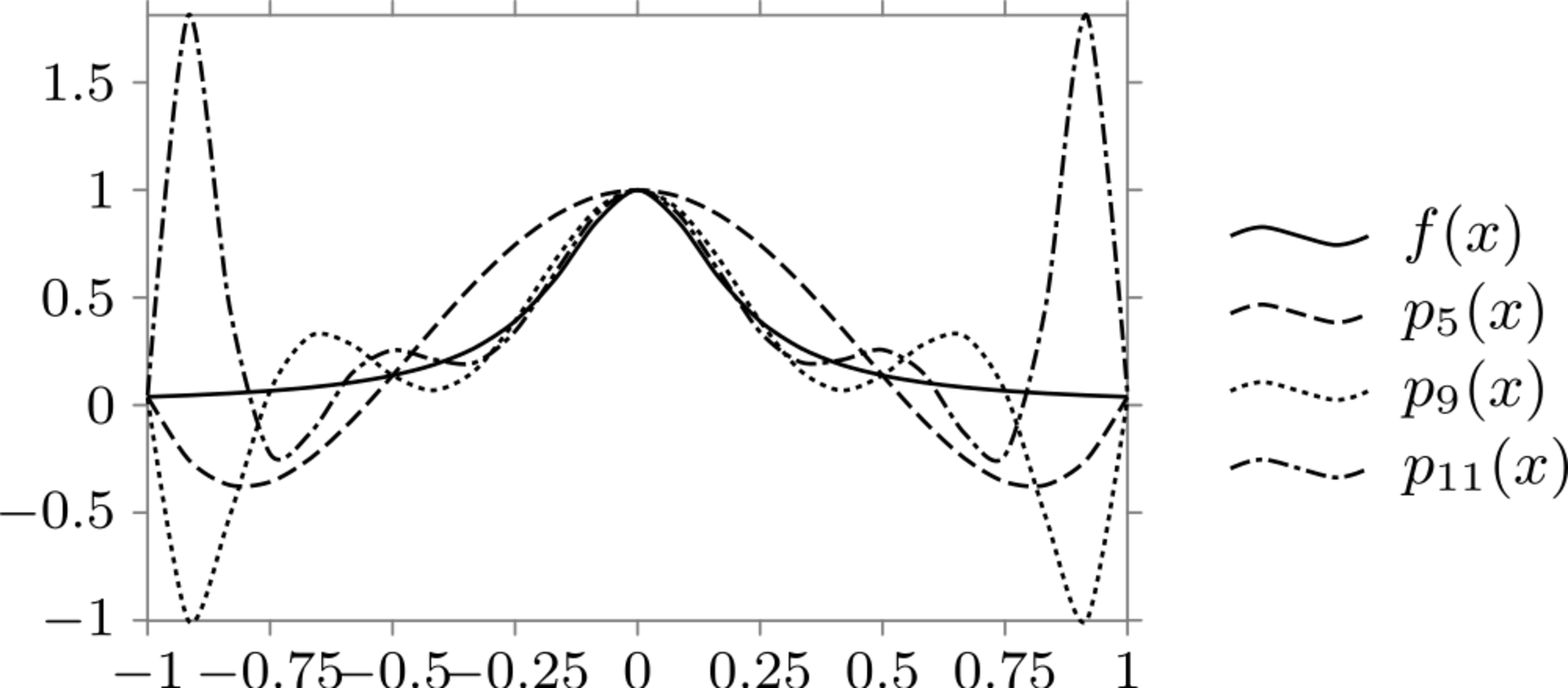ルンゲ現象
図によれば，補間多項式が通るべき点の個数$n$を増やすほど，$p_n(x)$は$f(x)$からかけ離れている．その様子は特に$x=\pm 1$付近で顕著である．このような現象をルンゲ現象という．
ルンゲ現象により，ニュートン・コーツの公式においてただ次数を増やしても，積分の近似値は改良されないと考えられる．複合台形則，複合シンプソン則などが利用されるのはこのためである．
ルンゲ現象を回避するには，補間多項式が通るべき点の$x$座標をチェビシェフノード
$$
x_i = \cos\pqty{\frac{2i-1}{2n} \pi}\quad (i = 1, \dots, n)
$$
にすると良いことが知られている[1]．このとき，$n=9$の下で補間多項式$p(x)$は下図のようになる．確かに$x=\pm 1$付近における振動が抑制されていることが分かる．
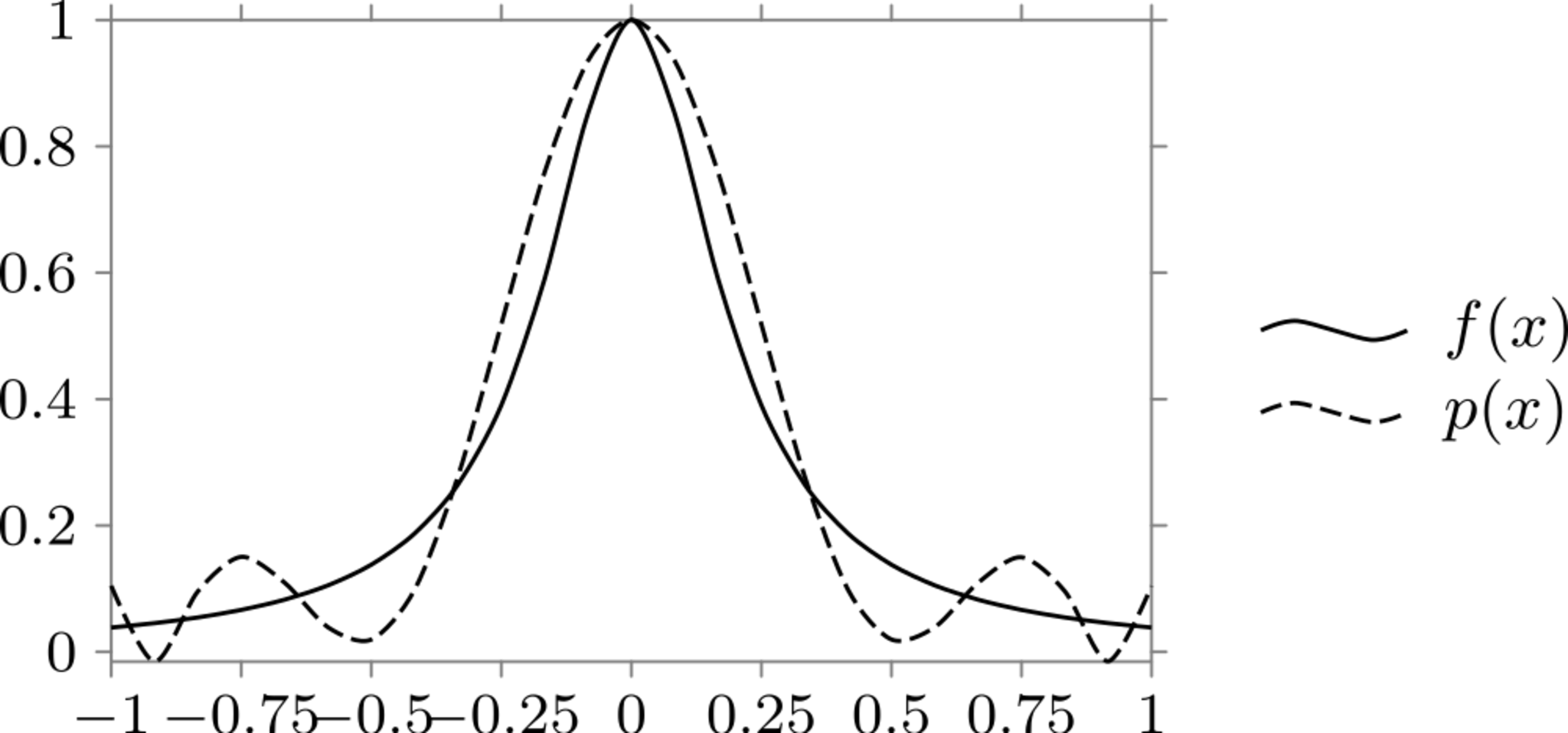チェビシェフノードを利用した補間多項式
補間多項式とテイラー多項式の関係
この節では，補間多項式がテイラー多項式の近似と見なせることを述べる．
点$t$のまわりで$n$階微分可能な関数$f(x)$に対して，次の多項式を$n$次のテイラー多項式という．
$$
p_n(x)=\sum_{k=0}^n \frac{f^{(k)}(t)}{k!} (x-t)^k=f(t)+f'(t)(x-t)+\cdots+\frac{f^{(n)}(t)}{n!} (x-t)^n
$$
関数$f(x)$が点$t$のまわりでテイラー展開可能であるとは，定義域における任意の$x$で
$$
f(x)=\lim_{n\to\infty} p_n(x)=\sum_{n=0}^\infty\frac{f^{(n)}(t)}{n!} (x-t)^n
$$
が成立することをいい，この級数で元の関数を表現することをテイラー展開という．
一般には，関数が何回でも微分可能であってもテイラー展開可能とは限らない．しかし，実用上よく表れる関数はしばしばテイラー展開可能である．たとえば，関数$\cos x,\sin x,e^x$は定義域における任意の点でテイラー展開可能である．
まず$n=2$のときについて考える．$2$次のテイラー多項式
$$
p_2(x)=f(t)+f'(t)(x-t)+\frac{f''(t)}{2}(x-t)^2
$$
について，この式に表れる微分係数を
$$
f'(t)\fallingdotseq\frac{f(t+h)-f(t)}{h},\quad f''(t)\fallingdotseq\frac{\pqty{f(t+h)-f(t)}h^{-1}-\pqty{f(t)-f(t-h)}h^{-1}}{h}
$$
のように，十分小さな$h$で近似することを考える．この近似は次のように書き換えられる．
$$
f'(t)\fallingdotseq f[t+h,t],\quad f''(t)\fallingdotseq 2\cdot\frac{f[t+h,t]-f[t,t-h]}{(t+h)-(t-h)}=2f[t+h,t,t-h]
$$
すると，これを$p_2(x)$に代入すれば
$$
p_2(x)\fallingdotseq f(t)+f[t,t-h](x-t)+f[t+h,t,t-h](x-t)^2
$$
となり，さらに，$h$が十分小さければ$x-(t+h)\fallingdotseq x-t$であるので
$$
p_2(x)\fallingdotseq f(t)+f[t+h,t](x-(t+h))+f[t+h,t,t-h](x-(t+h))(x-t)
$$
である．
定理1.3
により，右辺は点$(t-h,f(t-h)),(t,f(t)),(t+h,f(t+h))$に関する補間多項式である．
以下では一般の$n$についても，補間多項式がテイラー多項式の近似と見なせることを示す．
実数$x_1,\dots,x_{n+1}$はどの２つも相異なるとし，$x_1,\dots,x_{n+1}$の中で最小のものを$m$，最大のものを$M$とおく．また，関数$f(x)$は区間$I = [m, M]$で$n$階微分可能であるとする．このとき，次式を満たす$\xi \in (m, M)$が存在する．
$$
f[x_1,\dots,x_{n+1}] = \frac{f^{(n)}(\xi)}{n!}
$$
点$(x_1,f(x_1)),\dots,(x_{n+1},f(x_{n+1}))$に関する補間多項式を$p(x)$とおくと，関数$g(x)=f(x)-p(x)$は$x_1,\dots,x_{n+1}$を零点に持つ．したがって，
補題1.5
により$g^{(n)}(\xi)=0$を満たす$\xi\in (m, M)$が存在する．ここで，$p(x)$は
定理1.3
により
$$
p(x) = f(x_1) + \sum_{k=1}^{n} f[x_1,\dots,x_{k+1}] (x-x_1) \cdots (x-x_k)
$$
と表せる．よって$p^{(n)}(x) = f[x_1,\dots,x_{n+1}]n!$であり
$$
f^{(n)}(\xi) - f[x_1,\dots,x_{n+1}]n! = 0
\quad\therefore\,
f[x_1,\dots,x_{n+1}] = \frac{f^{(n)}(\xi)}{n!}
$$
が成立する．
なお，関数$f(x)$の零点とは$f(\alpha)=0$を満たす値$\alpha$のことである．
関数$f(x)$はある開区間$\mathring{I}$で$n$階微分可能かつ，$n$次導関数$f^{(n)}(x)$は$\mathring{I}$で連続とする．$t=x_{n+1}\in\mathring{I}$をある定数とし，実数$s=x_1\in\mathring{I}$は$s< t$を満たすとする．$J=[s,t]$とおく．$n$個の実数$x_1,\dots,x_n \in J$はすべて$s$の関数であり，任意の$s$について$x_1,\dots,x_{n+1}$はどの２つも相異なるものとする．
点$(x_1,f(x_1)),\dots,(x_{n+1},f(x_{n+1}))$に関する補間多項式を$p(x)$とおくと，$p(x)$は
$$
p(x) = f(x_1) + \sum_{k=1}^n f[x_1,\dots,x_{k+1}] (x-x_1) \cdots (x-x_k)
$$
と書ける．定理1により，各$f[x_1,\dots,x_{k+1}]$に対して
$$
f[x_1,\dots,x_{k+1}] = \frac{f^{(k)}(\xi_k)}{k!}
$$
を満たす$\xi_k\in J$が存在する．
関数$f^{(k)}(x)$は閉区間$J$で連続なので，$J$における最小値$m_k$，最大値$M_k$が存在する．また，$f^{(k)}(x)$は$\mathring{I}$で連続なので$m_k, M_k\to f^{(k)}(t)\quad (s\to t-0)$である．よって，はさみうちの原理により
$$
f[x_1,\dots,x_{k+1}] \to \frac{f^{(k)}(t)}{k!}\quad (s\to t-0)
$$
が成り立つ．したがって，任意の実数$x$について
$$
p(x)=f(x_1)+\sum_{k=1}^n f[x_1,\dots,x_{k+1}](x-x_1)\cdots (x-x_k)\to f(t)+ \sum_{k=1}^n \frac{f^{(k)}(t)}{k!} (x-t)^k \quad (s\to t-0)
$$
である．これにより$p(x)\to p_n(x)\quad (s\to t-0)$であるので，$s$と$t$が十分に近ければ$p(x)\fallingdotseq p_n(x)$であり，補間多項式をテイラー多項式の近似と見なせることが確かめられた．
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
