偏差値erからの手紙(問題編)

165

2021/08/24追記

　解答編を投稿しました。それなりに長かった以前の記事よりもさらに長いので、時間のあるときにお読みください。

　数学者Aからこのような手紙が送られてきた。

　先日、僕はあるゲームに参加した。そのゲームの参加者は僕を含めて4人で、僕は2位だった。
　ゲームにはスコアというものがあって、スコアが高ければ順位が上になる。
　ゲーム終了後、僕自身のスコアの偏差値を計算してみたんだ。そのとき、ふと気づいた。
　僕の偏差値を知るだけならば、3位と4位のスコアを完全に知る必要はなく、その積$P$だけを知っていればよい、と。
　1位と僕のスコア、それから$P$の値がうまく噛み合った上に、同順位の参加者がいなかったからね。

　Aの偏差値はいくらか。ただし、スコアは任意の実数値をとる。

　偏差値クイズ第2弾(第1弾はこちらを参照)。今回は、本記事の筆者である私が実際に受け取った手紙の送信者と内容を若干脚色してお届けする。~~ちなみに脚色前の内容は「暑中お見舞い申し上げます」だった。~~

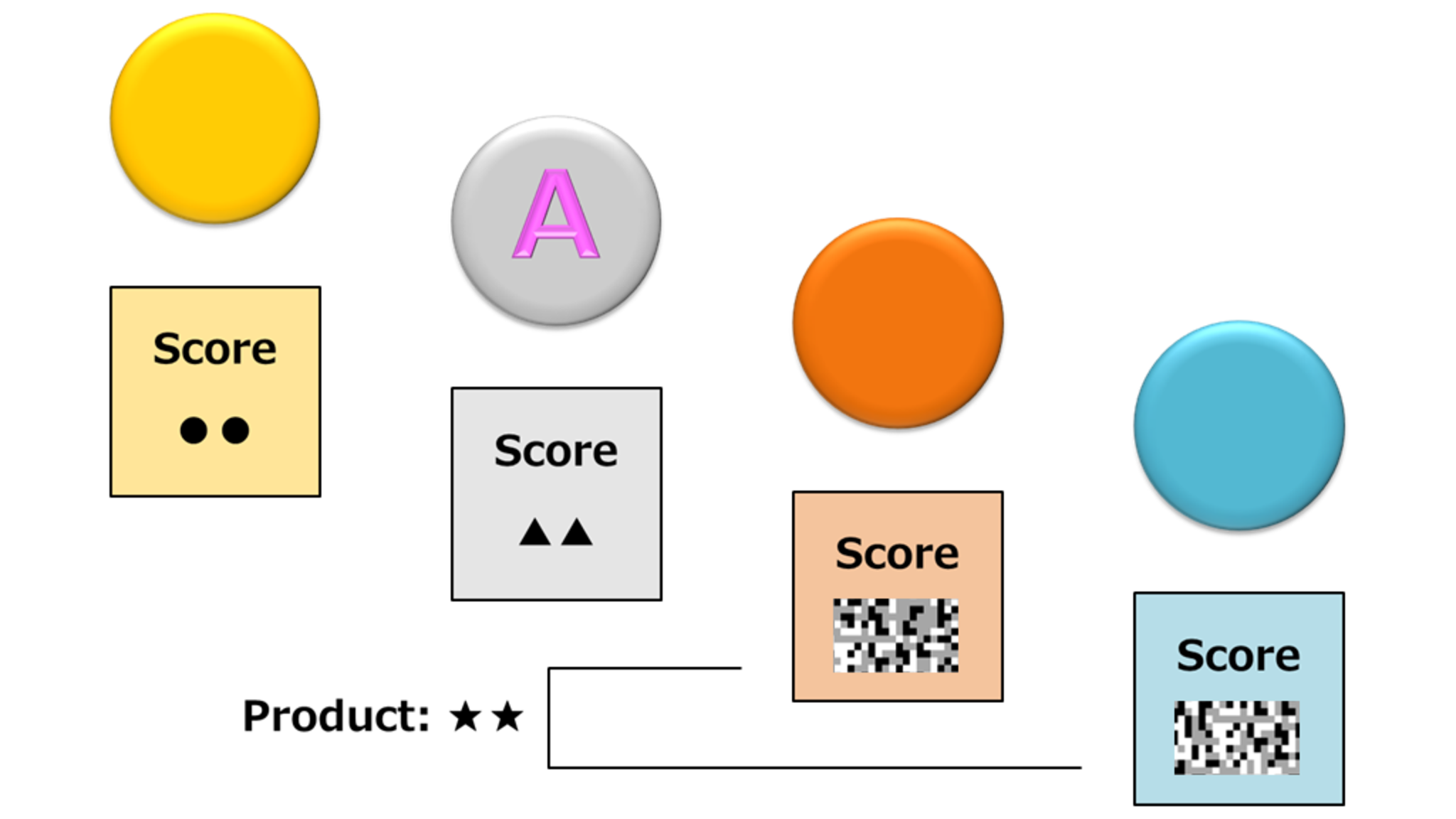
　さて、問題を見てみよう。1文目から唐突に現れた数学者Aなる人物が、どうやら当方に手紙を送り付けてきたらしい。Aの一人称は「僕」であるようだ。曰く、Aはこの手紙をしたためるより前に、何らかのゲームに参加した。そして、数学者としての性分からか、参加者のスコアデータを用いてA自身の偏差値を算出したとのこと。ここで「ふと気づいた」。
『1位のスコア』、『2位(つまりA)のスコア』、それから『3位と4位のスコアの積P』。この3つを知った時点で、Aの偏差値を求められたことに。通常であれば、全員のスコアの平均と分散を求め、標準偏差を計算し、偏差値の公式に代入して、ようやくAの偏差値が判る。しかしながらこのAという人物は、下位50％のスコアデータが欠落した状況においても自らの偏差値を確定させられる、という超レアな体験をしたそうだ。何とも羨ましい。

　……手紙を受け取った以上、とにかく彼(これは「彼もしくは彼女(they)」の略であり、性別の判明していないAを2021年8月時点における数学者のジェンダー・ステレオタイプから男性と決めつけているわけではないことを強調しておく)の偏差値を暴かねばならない。さあ、読者ならば本問をどのように解くだろうか。
　本問の解説記事は近日公開する、とだけ述べて、久々の記事執筆を終えることにする。解答は本記事のコメント欄、 Twitter のDMなど各所で受け付けている。

　(余談だが、巷では「〇〇を嗜む人」という意味で「〇〇er」なる単語が生成されていると聞く。例えば、「競プロer」で「競技プログラミングを嗜む人」、「数オリer」で「数学オリンピックを嗜む人」、「September」で「Septembを嗜む人」、といった風に。その慣習に従って、数学者Aを「偏差値を嗜む人」、すなわち「偏差値er」と評し、本記事のタイトルとした。)

投稿日：2021年8月22日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

匿(Tock)

168

22436

主に初等幾何・レムニスケート。時々偏差値・多重根号。「たとえ作曲家が忘れ去られた日であっても、彼の旋律が街並みを縫って美しく流れていますように。」

他の人のコメント

コメントはありません。

読み込み中

匿(Tock)

偏差値erからの手紙(問題編)