ゲージ対称性とは何か(10): 拘束を無闇に使うと誤る系

この記事は「 ゲージ対称性とは何か(9):なぜ「Diracの予想」を"信奉"するのか？ 」の続きです。

Notationをまとめておきます：

• $\{\cdot,\cdot\}$はPoisson bracketを表す
• 一般に、空間ベクトル$\vec \alpha=(\alpha_x,\alpha_y,\alpha_z)$は上付き添字$\alpha^i:(\alpha^1,\alpha^2,\alpha^3)$に対応。微分は下付き添字$\partial_i:(\partial_1,\partial_2,\partial_3)$が$(\partial/\partial x,\partial/ \partial y,\partial/ \partial z)$に対応
• 運動方程式をEoM（Equation of Motion）と表す
• E-L eq.はオイラー・ラグランジュ方程式のこと（Euler-Lagrange equation）
• 「拘束の時間発展に対する無矛盾性」＝「拘束が時間発展で保たれる」ことをc.t.e.（consistency of time evolution）と表す

  ---

慎重な扱いを必要とする特異系

次のLagrangianに従う系を考えます(Ref.[1])：

後述しますが、この系は、磁場中の荷電粒子の運動に対応します。
まずはDiracの方法に則った正しい正準形式の議論を展開します。次に、この系では無闇に拘束を使うと間違った答えを導くことを述べます。
その後「第１類拘束条件はゲージ変換の生成子」であることに言及し、最後に物理的背景を述べて終わりにします。

Lagrange形式

最初にE-L eq.を導いておきます：
\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot q^1}-\frac{\partial L}{\partial q^1}=0\ &\leftrightarrow \ \dot q^2=-q^1\\ \frac{d}{dt}\frac{\partial L}{\partial \dot q^2}-\frac{\partial L}{\partial q^2}=0\ &\leftrightarrow \ \dot q^1=q^2 \end{align}

これは正しい運動方程式です。
拘束の取り扱いに悩んだら、Lagrange形式に戻りましょう。

正準形式：Diracの方法を用いた正しい議論

次に正準形式で議論します。
まずは拘束系の取り扱いに基づいて議論します。

第１次拘束条件とHamiltonian

拘束条件とHamiltonianを導きます。canonical momentumは
\begin{align} p_1&=\dfrac{\partial L}{\partial \dot q^1}=-q^2,\\ p_2&=\dfrac{\partial L}{\partial \dot q^2}=q^1 \end{align}
です。この2式は位置の時間微分$\dot q^1,\dot q^2$を含みません。つまり拘束条件です。これらを
\begin{align} \phi^1:&=p_1+q^2,\\ \phi^2:&=p_2-q^1 \end{align}
とします。

Hamiltonianはcanonical momentumを用いて
\begin{align} H&=p_1\dot q^1+p_2\dot q^2-L\\ &=-q^2\dot q^1+q^1\dot q^2-(q^1\dot q^2-q^2\dot q^1 +(q^1)^2+(q^2)^2)\\ &=-({q^1})^2-({q^2})^2 \end{align}
となります。

$\tilde H$による時間発展

拘束条件間のPoisson bracketは
\begin{align} \{\phi_1,\phi_1\}&=\{\phi_2,\phi_2\}=0,\\ \{\phi_1,\phi_2\}&=2 \end{align}
よってこれらは第２類拘束条件です。

いま
$$\tilde H:=H+\lambda^1\phi_1+\lambda^2\phi_2$$
とすると
\begin{align} \dot\phi_1&=\{\phi_1,\tilde H\}=\{\phi_1,H\}+\lambda^2\{\phi_1,\phi_2\},\\ \dot\phi_2&=\{\phi_2,\tilde H\}=\{\phi_2,H\}+\lambda^1\{\phi_2,\phi_1\} \end{align}
ここで
\begin{align} \{\phi_1,H\}&=2q^1,\\ \{\phi_2,H\}&=2q^2 \end{align}
以上から未定係数は
\begin{align} \dot \phi_1&=2q^1+2\lambda^2\approx 0,\\ \dot \phi_2&=2q^2-2\lambda^1\approx 0.\\ \therefore \lambda^1&=q^2, \ \lambda^2=-q^1 \end{align}
と定まります。これはまた、$\phi^1,\phi^2$のc.t.e.が成立し、他に拘束が存在しないことを意味します。
この系には第１次拘束しか存在しないので、$\tilde H=H_E=H_T$です。$\tilde H$は上で求めた$\lambda$より
\begin{align} \tilde H=q^2p_1-q^1p_2 \end{align}
となります。

$\tilde H$よりcanonical EoMは
\begin{align} \dot q^1&=\{q^1,\tilde H\}=q^2,\\ \dot q^2&=\{q^2,\tilde H\}=-q^1,\\ \dot p_1&=\{p_1,\tilde H\}=p_2,\\ \dot p_2&=\{p_2,\tilde H\}=-p_1 \end{align}
下2つの運動方程式は、$p_1=-q^2, \ p_2=q^1$より、上2つの方程式とconsistentです。また、最初に導いたE-L equationともconsistentであることはすぐにわかります。

Dirac brackets

Dirac bracketを計算しておきましょう。
\begin{align} C&=\{\phi^i,\phi^j\}\\ &=\begin{pmatrix} 0 & 2\\ -2 & 0 \end{pmatrix} \\ \therefore C^{-1}&= \begin{pmatrix} 0 & -1/2\\ 1/2 & 0 \end{pmatrix} \end{align}
つぎに$\{q^i,\phi^\alpha\}$を計算します:
\begin{align} \bullet \ &\{q^1,\phi^1\}=\{q^1,p_1+q^2\}=1,\\ \bullet \ &\{q^1,\phi^2\}=\{q^1,p_2-q^1\}=0,\\ \bullet \ &\{q^2,\phi^1\}=\{q^2,p_1+q^2\}=0,\\ \bullet \ &\{q^2,\phi^2\}=\{q^2,p_2-q^1\}=1\\ &\therefore \{q^i,\phi^\alpha\}= \begin{pmatrix} 1&0\\ 0&1 \end{pmatrix} \end{align}
さらに$\{p_i,\phi^\alpha\}$を計算します：
\begin{align} \bullet \ &\{p_1,\phi^1\}=\{p_1,p_1+q^2\}=0,\\ \bullet \ &\{p_1,\phi^2\}=\{p_1,p_2-q^1\}=1,\\ \bullet \ &\{p_2,\phi^1\}=\{p_2,p_1+q^2\}=-1,\\ \bullet \ &\{p_2,\phi^2\}=\{p_2,p_2-q^1\}=0,\\ &\therefore \{p_i,\phi^\alpha\}= \begin{pmatrix} 0&1\\ -1&0 \end{pmatrix} \end{align}
よってDirac bracketsは以下のようになります:
\begin{align} \{q^i,p_j\}_D&=\{q^i,p_j\}-\{q^i,\phi^\alpha\}C^{-1\alpha\beta}\{\phi^\beta,p_j\}\\ &= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} - \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & -1/2\\ 1/2 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}\\ &= \begin{pmatrix} 1/2 & 0\\ 0 & 1/2 \end{pmatrix} \end{align}
\begin{align} \{q^i,q^j\}_D&=-\{q^i,\phi^\alpha\}C^{-1\alpha\beta}\{\phi^\beta,q^j\}\\ &=- \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & -1/2\\ 1/2 & 0 \end{pmatrix} \begin{pmatrix} -1 & 0\\ 0 & -1 \end{pmatrix}\\ &= \begin{pmatrix} 0 & -1/2\\ 1/2 & 0 \end{pmatrix} \end{align}
\begin{align} \{p_i,p_j\}_D&=-\{p_i,\phi^\alpha\}C^{-1\alpha\beta}\{\phi^\beta,p_j\}\\ &=- \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix} \begin{pmatrix} 0 & -1/2\\ 1/2 & 0 \end{pmatrix} \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix}\\ &= \begin{pmatrix} 0 & 1/2\\ -1/2 & 0 \end{pmatrix} \end{align}

以上より、Dirac bracketsから導かれるEoMは
\begin{align} \dot q^1&=\{q^1,H\}_D=\{q^1,-(q^1)^2-(q^2)^2\}\\ &=-2q^1\{q^1,q^1\}_D-2q^2\{q^1,q^2\}_D\\ &=q^2,\\ \dot q^2&= \{q^2,H\}_D=-q^1,\\ \dot p_1&= \{p_1,H\}_D=q^1,\\ \dot p_2&= \{p_2,H\}_D=q^2 \end{align}
となります。

Dirac bracketの中では、弱い等式を強い等式として扱ってよい（つまりは拘束をゼロにしてよい）ので、$H$も$\tilde H$も等価であることに注意してください。
これらのEoMは、これまで導いたEoMとconsistentです。

$H$による間違った時間発展

ここで、$\tilde H$ではなく$H$からEoMを導いてみます。
\begin{align} \dot q^1=\{q^1,H\}=\{q^1,-(q^1)^2-(q^2)^2\} \end{align}
これは、拘束を使わなければ0だし、拘束を使うと
\begin{align} =\{q^1,-p_2^2-p_1^2\}=-2p_1 \end{align}
となり、おかしな結果を導きます。$q^2$も拘束条件を使うと
\begin{align} \dot q^2&=\{q^2,H\}=\{q^2,-(q^1)^2-(q^2)^2\}\\ &=\{q^2,-p_2^2-p_1^2\}=-2p_2 \end{align}
となりおかしいです。

このような混乱を起こさないためには、拘束を用いて変数を書き換えるようなことをせず、$\tilde H$を構成してそれによる時間発展を計算する。またはDirac bracketを導いておき、これを使って時間発展を計算するのが良いです。

第１類拘束とゲージ対称性

ところで、この系にはゲージ対称性は存在しません。
実際探してみると無さそうのはわかります。
しかし具体的に探さなくても、存在しないことが言えます。
それは、この系の拘束$\phi_1,\phi_2$は第２類：
$$ \{\phi_1,\phi_2\}=\{p_1+q^2,p_2-q^1\}=2\not \approx 0 $$
であり、第１類拘束条件ではないからです。

なぜゲージ対称性は第１類拘束に関わるかというと、$H_E$形式では、ゲージ対称性は定まらない未定係数と第１類拘束で生成されるからです（Ref.[2]）。
$H_E$は以下のように表せます：
$$ H_E=H'+\phi^a_{\rm 1cl}\lambda_{{\rm 1cl},a} $$
ここで$H'$は、元の$H$と、第２類拘束を含む部分です:
$$ H':=H+\lambda_{{\rm2cl},a}\phi_{\rm 2cl}^a $$
$\lambda_{{\rm 2cl},a}$はc.t.e.より定まるので、$H'$は$H_E$の確定している部分です。一方で$\lambda_{{\rm 1cl},a}$は定まりません。

$H_E$による$q^i,p^i$の時間発展は
\begin{align} \dot q^i&=\{q^i,H'\}+\{q^i,\phi^a_{\rm 1cl}\}\lambda_{{\rm 1cl},a},\\ \dot p^i&=\{p^i,H'\}+\{p^i,\phi^a_{\rm 1cl}\}\lambda_{{\rm 1cl},a} \end{align}
ですが、$\lambda_{{\rm 1cl},a}$が定まっていないため、
$$ \delta q_i(t)=\{q^i,\phi^a_{\rm 1cl}\}, \ \ \ \delta p_i(t)=\{p^i,\phi^a_{\rm 1cl}\} $$
の方向には運動が定まりません（これらPoisson bracketは一般にはゼロではない）。
つまり、系はこれら変換の係数$\lambda_{{\rm 1cl},a}(t)$という任意関数に対する不変性を持ちます。
これはゲージ対称性に他なりません。

物理的側面

2次元内の荷電粒子が磁場中に存在するとき、Lagrangianは以下のように書けます(Ref.[3])：
\begin{align} L(q,\dot q)=\frac{1}{2}m (\dot q^i)^2+e A^i(q)\dot q^i-V(\vec q) \ \ \ (i=1,2) \tag{1} \end{align}
$A^i$は電磁場のベクトルポテンシャル、$V$はなんらかの外的なポテンシャルです。電場が存在しない系を考えるので、$A$は顕わには時間に依存しません（$E^i$は$\partial A^i/\partial t$を含むことに注意）。$eA^i\dot q^i$がいわゆるLorentz力に対応します（Appendixにそれらの対応を記しておきます）。

磁場が$z$方向を向いているとします。$\vec A$を
\begin{align} \vec A=\left(-\frac{B}{2}q^2,\frac{B}{2}q^1,0\right) \end{align}
とすると、磁場$\vec B$は
\begin{align} \vec B={\rm rot}\vec A=(0,0,B) \end{align}
となります。確かに$z$方向を向いています。

この$\vec A$をEq.(2)に入れれば
\begin{align} L=\frac{m}{2}((\dot q^1)^2+(\dot q^2)^2)+\frac{eB}{2}(q^1\dot q^2-q^2\dot q^1)-V(q^1,q^2) \end{align}
を得ます。

ここで、この系では磁場が非常に強く、運動項$\frac{m}{2}((\dot q^1)^2+(\dot q^2)^2)$を無視できるとします。そして
\begin{align} V=-((q^1)^2+(q^2)^2) \end{align}
（anti-harmonic potential）とします（図２参照）。あとは$eB/2$を1にしたら、冒頭のLagrangianになります。

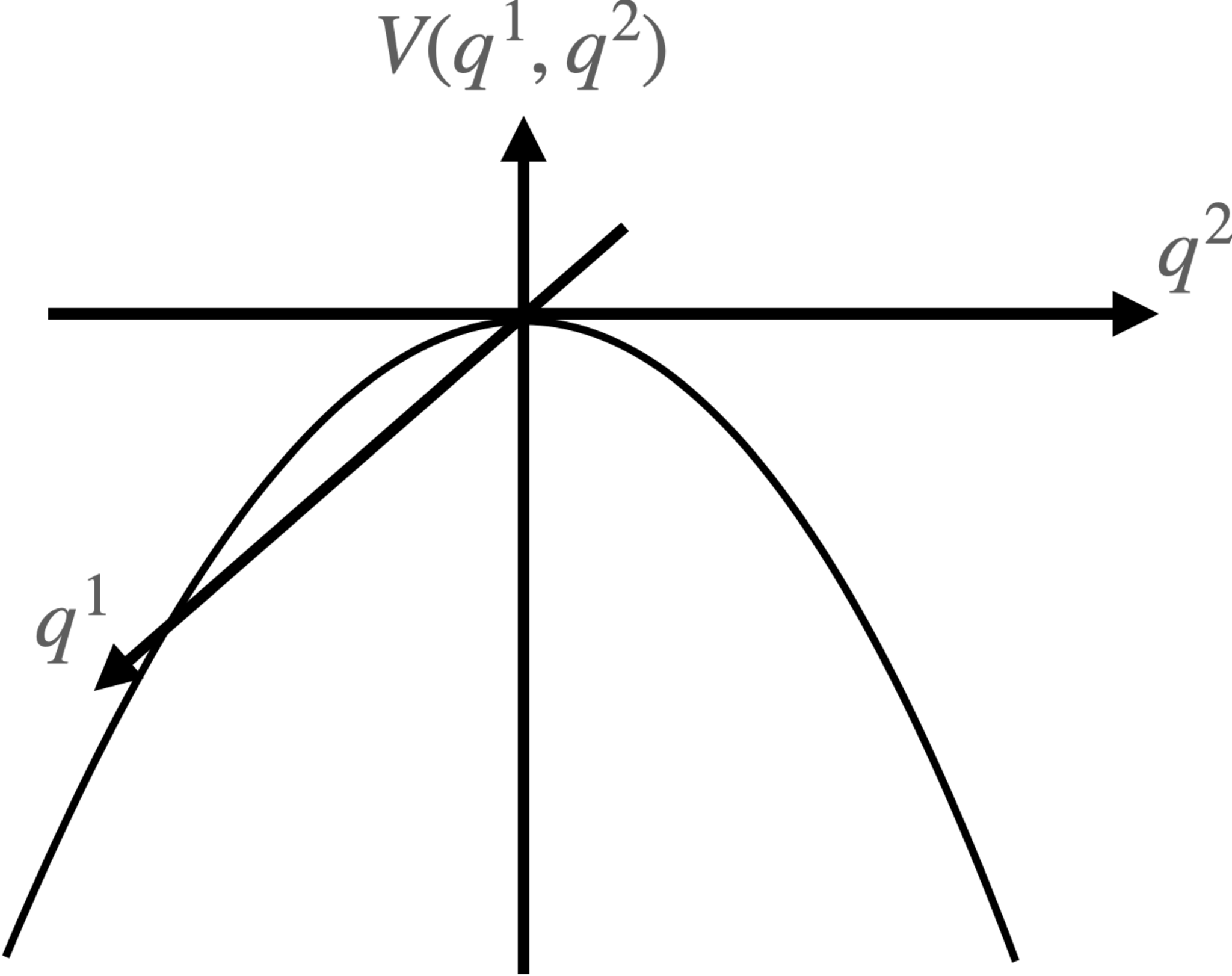外的ポテンシャルの形

この系の運動方程式をLagrange形式で書くと
\begin{align} \dot q^1=q^2,\\ \dot q^2=-q^1 \end{align}
でしたが、これの解は円運動です：
\begin{align} q^1&=A\sin(t+\delta),\\ q^2&=A\cos(t+\delta) \end{align}
このように$q^1,q^2$は独立ではなく拘束されています。対応して、初期条件に対応するパラメータもが2つしかありません。
これらは、相空間で2つ、位置・速度空間で1つの拘束が存在することを表しています。

上記の運動は、粒子の初期位置を通り、ポテンシャルの原点を中心とする円運動です。つまり初期位置のみで運動が定まります。
この事情は、運動項を無視すると、E-L eq.は力の釣り合いの式になることに由来します。

粒子に働く力はLorentz力$\vec F_L=(2\dot q^2,-2\dot q^1)$と外的ポテンシャルによる力$\vec F_V=(2q^1,2q^2)$です。E-L eq.はこれらが打ち消し合うことを要求します。よって、Lorentz力$\vec F_L$は円の中心を向いています（図２参照）。ここで、磁場は$z$軸正の方向、力は円の中心を向いているので、速度の方向はそれらに垂直すなわち円の接線方向になります。さらに、右ねじの法則から、速度は接線方向右回り（$z$軸負の方向に見て）であることもわかります（図２参照）。実際、上記の円運動の解は右回りです。また、円運動になるためには、角速度にも制限がつきます。

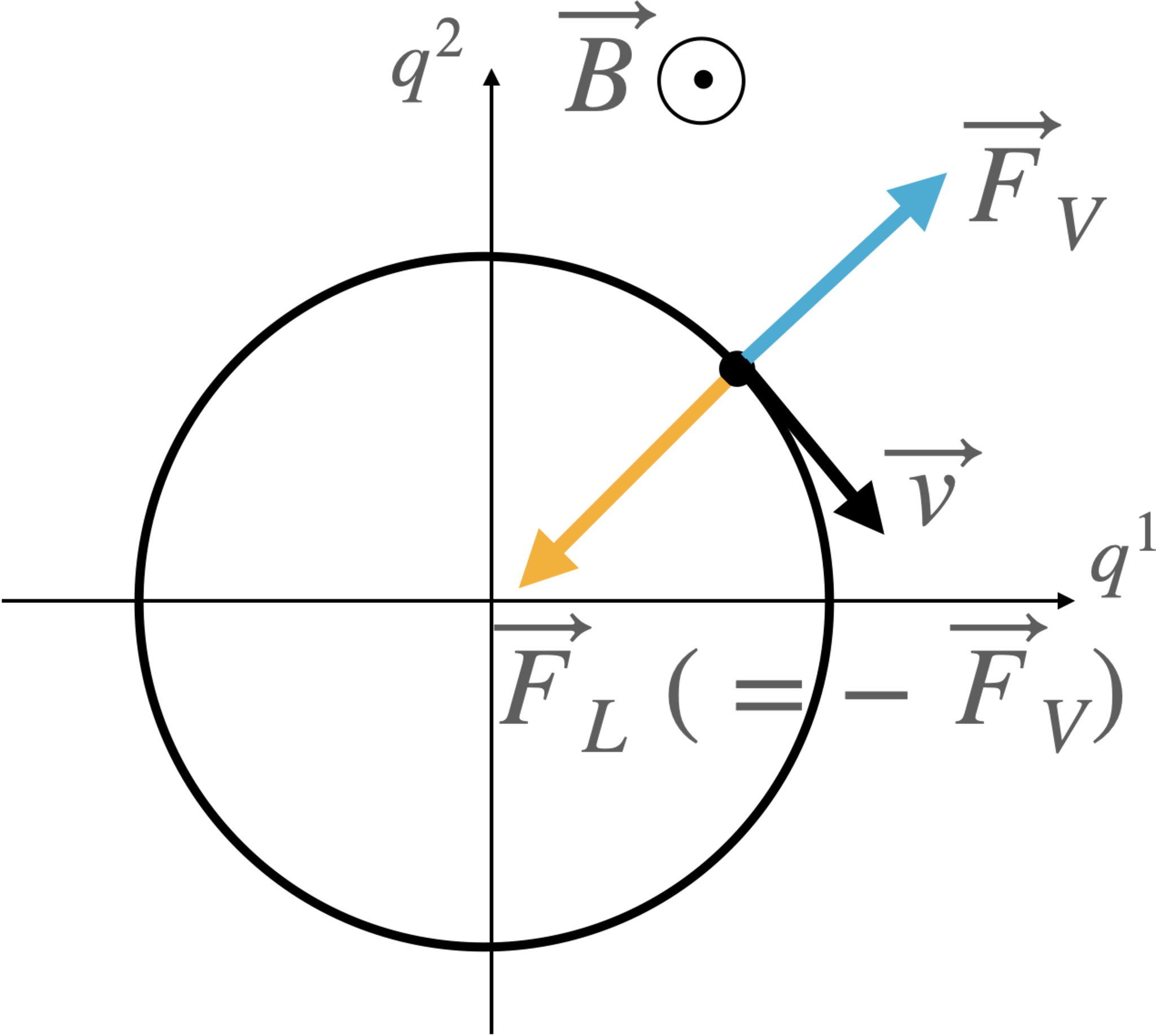力の釣り合いと速度の方向

この運動は、サイクロトロン運動のような「自然に起こる円運動」とは違うように思います。
物理的には、実際に起こる運動というより、
「この系の運動としてconsistentなのは、上記の円運動だ」
程度に解釈したほうがよいように思います。

まとめ

今回は磁場中の荷電粒子に対応するLagrangianを考察しました。
まとめると

という感じです。

最後に、この系が拘束系である原因は、時間微分と位置座標がカップルした$q^1\dot q^2-q^2\dot q^1$のような項が存在するからです。このような項は、自由Fermion $\psi$のLagrangianに含まれる
$$ \bar \psi\gamma^\mu i\partial_\mu \psi $$
（$\gamma_\mu$はDirac行列と呼ばれる、Clifford代数の元）にも現れます。

おしまい。${}_\blacksquare$

☆次の記事： ゲージ対称性とは何か(11)：経路積分量子化におけるFaddeev-Popovの方法

Appendix: Eq.(1)が磁場中の荷電粒子の運動に対応する事の説明

Eq.(2)からE-L eq.を導いてみます：
\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot q^i}&=m\ddot q^i+e\dot A^i(q)=m\ddot q^i+e\dot q^j (\partial_j A^i),\\ \frac{\partial L}{\partial q^i}&=e\dot q^j\partial_i A^j-\partial_i V \end{align}
ただし、$\partial_jA^i, \partial_i V$は$\frac{\partial}{\partial x^j}A_i(x)|_{x=q}, \frac{\partial}{\partial x_i}V(x)|_{x=q}$のこと。よって
\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot q^i}-\frac{\partial L}{\partial q^i}=m\ddot q^i+e\dot q^j(\partial_j A^i)-e\dot q^j\partial_i A^j+\partial_i V \tag{A1} \end{align}

さて、磁場中の荷電粒子が受けるLorentz力は、時刻$t$において
$$ (\vec F(t))^i=e(\vec v(t)\times \vec B(q(t))^i $$
です。「Lorentz力は、速度と磁場の方向に垂直である」というやつですね。
これは
\begin{align} (\vec F(t))^i&=e(\vec v(t)\times \vec B(q(t))^i\\ &=e(\vec v\times({\rm rot} \vec A))^i\\ &=e\epsilon_{ijk}\dot q^j(\epsilon_{klm}\partial_lB^m) \\ &=e[\dot q^j(\partial_i A^j)-\dot q^j(\partial_jA^i)] \end{align}
と書けます。よって、Eq.(A1)は
\begin{align} m\ddot q^i-e(\vec v\times B)^i +\partial_i V \end{align}
なので、EoMは
\begin{align} m\ddot q^i-e(\vec v\times B)^i +\partial_i V=0\\ \leftrightarrow m\ddot q^i=e(\vec v\times B)^i -\partial_i V \end{align}
となります。確かに磁場中（および外的ポテンシャル中）の荷電粒子の運動方程式と一致しています。${}_\blacksquare$