ゲージ対称性とは何か(11)：経路積分量子化におけるFaddeev-Popovの方法

本記事は「 ゲージ対称性とは何か(10): 拘束を無闇に使うと誤る系 」の続きです。

今回は、経路積分におけるゲージ理論の量子化のひとつの方法である

（以下FP, FPの方法と略す）

に関して述べようと思います。
基本どんな場の量子論の教科書にも書いてあることではあるのですが、この後Gribov問題に関して触れるのに言及しておいたほうがいいので、書いておこうかなと思った次第です。

参考文献としてRef.[1-3]を挙げておきました。また、以下Yang-Mills理論を扱いますが、これに関してはこれら参考文献、または「 ゲージ対称性とは何か(８)：Yang-Mills理論とDiracの方法 」を御覧ください。

申し訳ないですが、経路積分の知識は基本的に既知とします。参考文献やネット上の記事を御覧ください。
その直感的理解はAppendix(b)に少しだけ解説しておきます。

また今回、小話から始まります。
これを飛ばして「Faddeev-Popovの方法」から読んでいただいても、たぶん大丈夫です。
もちろん小話だけ読んで頂いても...

人類金太郎飴平面

20〇〇年、とうとう人類は地球外知的生命体Xとの通信に成功しました。
遠い星にいるので直接会うことは叶いませんが、データを送受信することはできます。
人類は様々なデータをXに送りました。

遠い星にいる宇宙人Xとのコンタクトに成功！

ある日Xから「人類全員の顔の画像を送ってほしい」と言われました。
そこで、宇宙担当大臣の進○郎さんは、「人類金太郎飴平面」を作るというアイディアを考えました。

進次○さんと典型的な金太郎飴

「人類金太郎飴平面（以下人金面と略す）」とは、人類全員の"金太郎飴"を作り、それをならべて"平面"を作ったものです。

図3が人金面の図です。細長い方向を横にして、それぞれの人の金太郎飴を縦方向に並べます。顔が似た人は近いところに配置します。そしてこの"金太郎飴"は、普通のとは異なり、各断面の表情が違います。ある所で切れば笑顔、ある所では怒り顔、ある所では泣き顔のように、どんどん表情が変わります。

人金面の図

そして○次郎さんは、この人金面を以下のオレンジ色の線=笑顔の線で切り、その切断面の画像をXに送りました。

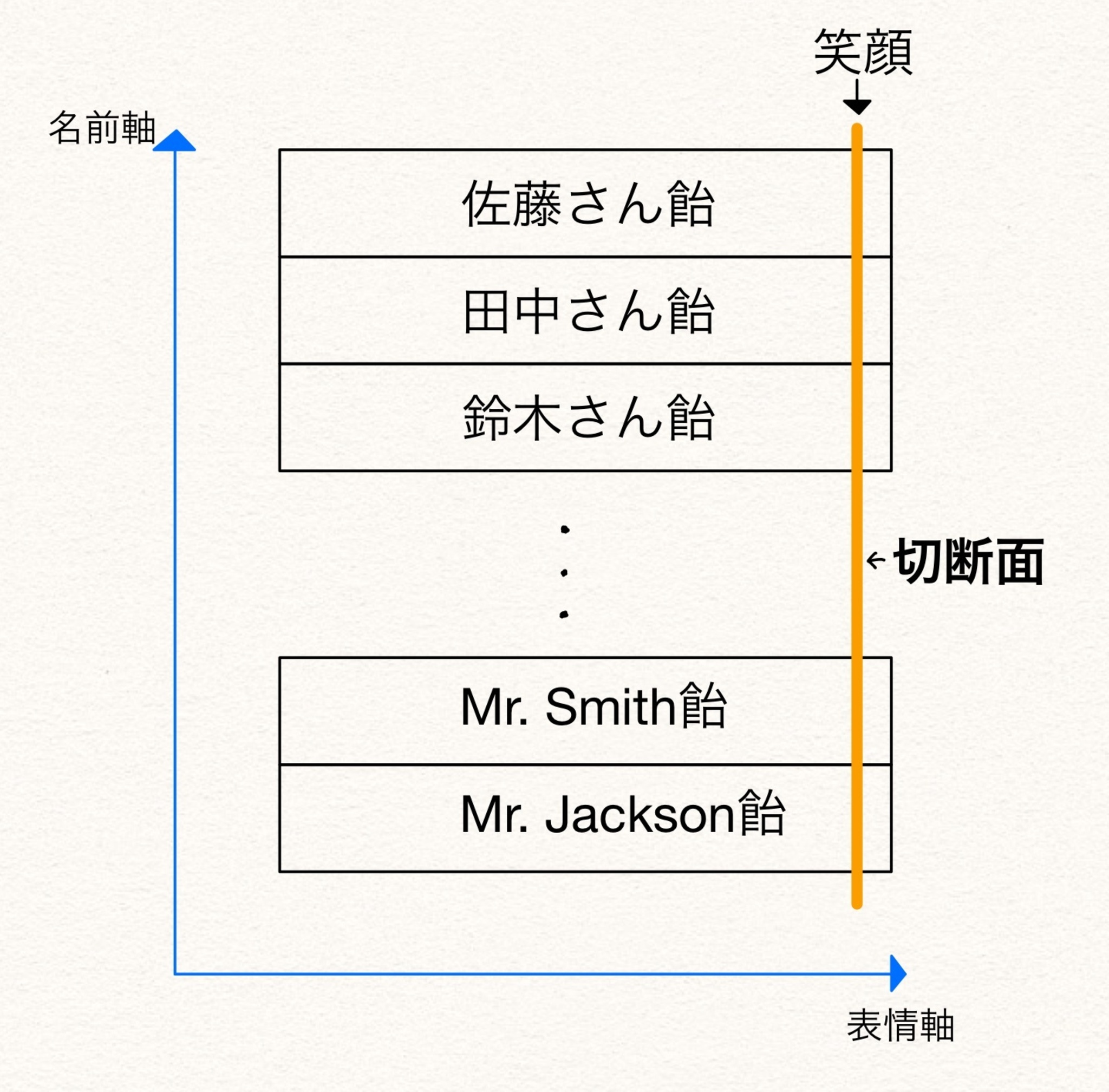人金面：笑顔の切断面

人金面の、表情軸に沿った情報は冗長です。笑顔も泣き顔も怒り顔も、どれであれ「その人」であることは変わりません。宇宙人の要求に応えるには、どれか１つの表情で十分です。

FPの方法と人金面の類似性

FPの方法でも同じようなことをします。

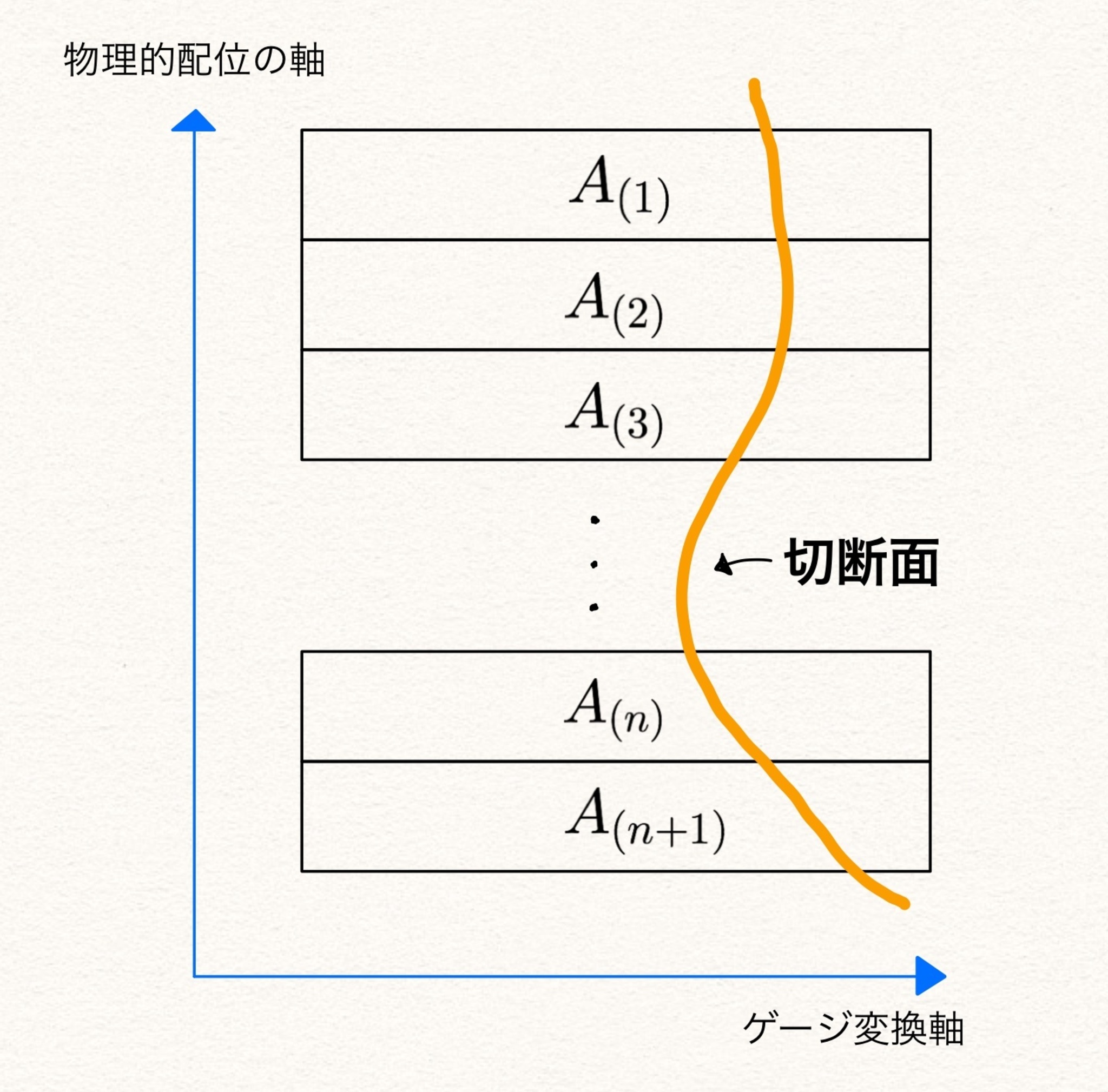FPの方法...ゲージ場の汎関数空間を切断する

人金面との類似性を保つため、ゲージ場$A$の汎関数空間を離散化します（実際にはFPは連続極限での話です）。
$A$の空間を「物理的に異なる配位」と「ゲージ変換」の軸で記述します。
(「物理的に異なる配位」とは、すなわち「ゲージ変換で結びつかない配位」のことです)
そして物理的に異なる配位の足を$i$、ゲージ変換の足を$\theta$とします。
これによりゲージ場$A$を$A^\theta_{(i)}$とラベルします。
また、各$i$におけるオレンジの線での$A^\theta_{(i)}$の切断面を$\tilde A^\theta_{(i)}$とします。
すると、ゲージ不変な何らかの汎関数$f$の汎関数空間での和（〜汎関数積分）は
$$ \sum_{\{A\}} f(A)=\sum_\theta \sum_i f(\tilde A^\theta_{(i)}) \Delta_i $$
と書けます。ここで$\Delta_i$は$A_{(i)}$における切断面の傾きを補正するファクターです。また実際のFPの方法では、切断面をデルタ関数で指定します。

和の中は$\theta$の依存性のないように書くことができます（次の章で述べます）。よって$\sum_\theta$の和がくくりだせます。この和は冗長だし、そして発散しています。あとはこれを捨てるなりなんなりすればよいです。

これがFPの方法の精神です。

Faddeev-Popovの方法

FPの方法を述べます。以下Yang-Mills理論における分配関数
\begin{align} &\int {\cal D}A \exp(i S) \end{align}
を考えます。この量に馴染みの無い方は、Appendix(a-1)を御覧ください。また$\int {\cal D}A$の意味は参考文献、ネット上の記事、またはAppendix(b)をご参照ください。

ゲージ場の汎関数積分を、ゲージ変換方向と、物理的に異なる状態に分解するため、その分け方（=図5のオレンジの曲線）をデルタ関数$\delta (F(A^\theta))$で指定します：
$$\int {\cal D}A \exp(S) \rightarrow \int {\cal D}\theta \int {\cal D}A^\theta \ \delta (F(A^\theta)) \exp(S) \tag{1}$$
$A^\theta(x)$は$A(x)$を$U(\theta)=\exp(ig \theta(x))$によりゲージ変換した量で
$$ A^{\theta} = \frac{i}{g}U\partial_\mu U^{-1}+UA_\mu U^{-1} $$
です。ここで課した条件$F(A^\theta)=0$は、すなわちゲージ固定条件です。

このままだとEq.(1)の矢印の左右の式はイコールではありません。等しくするためには、Jacobianをかける必要があります。これは、図5で言えば、オレンジの曲線が物理的に異なる状態を横切る角度の違いを調整するファクターです。
次の公式

を用いて変形します。ここで$\Delta_F(A)$がJacobianです。

改めて
$$ \int {\cal D}A \ \exp(iS) $$
に
$$ \Delta_F(A)\int{\cal D}\theta\delta(F(A^\theta)) \ (=1) $$
をかければ
$$\int {\cal D}A \ \exp(i S) = \int {\cal D}\theta \int {\cal D}A^\theta \ \exp(i S)\delta (F^\theta)\Delta_F(A)$$
が成立します。

ここで${\cal D}A$はゲージ変換で不変:
$$ {\cal D}A={\cal D}A^\theta $$
です。また${\cal D}\theta$も$\theta$のシフトに対し不変：${\cal D}(\theta\theta')={\cal D}\theta$です。
そして$\Delta_F(A)$もゲージ変換で不変です。なぜなら
\begin{align} (\Delta_F(A^\phi))^{-1}&=\int {\cal D}\theta \delta(F(A^{\theta+\phi}))\\ &=\int {\cal D}(\theta\phi) \delta(F(A^{\theta+\phi}))\\ &=\int {\cal D}(\theta') \delta(F(A^{\theta'}))\\ &=(\Delta_F(A))^{-1} \end{align}
だからです。さらに$\exp(i S)$もゲージ不変です。よって$A^\theta\rightarrow A$の変換を施せば
$$\int {\cal D}A \exp(S) = \int {\cal D}\theta \int {\cal D}A \ \exp(S)\delta (F)\Delta_F(A)$$
となります。

つぎに$\Delta_F(A)$を計算します。ここで$F$として、共変的な形
\begin{align} F=\partial_\mu A^{\mu a}-B^a \end{align}
を採用します。$B^a$はなんらかの場です。
このとき
\begin{align} \Delta_F(A)&= {\rm Det}(M^{ab}(x,y)),\\ M_{ab}(x,y)&=\partial^\mu D^{a}_{b\mu}\delta(y-x)|_{F(A)=0} \end{align}
となります。

以上から

と書けます。

重要なのは、$\int{\cal D}\theta$以外の部分
\begin{align} \int{\cal D}A \ {\rm Det}(M^{ab}(x,y))\delta(\partial A-B)\exp(iS) \end{align}
は$\theta$非依存なので、$\int {\cal D}\theta$が自明に積分できることです。この「ゲージ体積」を$V$とすれば
$$ \int {\cal D}A \ \exp(iS)=V\int{\cal D}A \ {\rm Det}(M^{ab}(x,y))\delta(\partial A-B)\exp(iS) $$
となります。
$V$は発散しています。

これらの作業は結局

ということをしています。

このように変形したのは、単に便利な表式だからではありません。実はゲージ体積を外にくくりださないと、その無限大性のために、そもそも積分がきちんと定義されません。これは重要なことなのですが、本文に入れると話が長くなるため、Appendix(a)で言及します。

局所場の形で書き直す

ということでめでたしめでたし、と言いたいとこなのですが、この形だとまだ使いにくいです。

場の理論のスタンダードな計算方法は摂動論です。摂動論は、ある理論のHamiltonianを、すでに解けている部分（〜対角化可能な部分、無摂動部分）とそれ以外にわけ、「それ以外」の部分の影響が無摂動部分に対して小さいとして、展開を用いて近似的に計算する手法です。この手法が使えるためには、計算に必要なパーツがすべてLagrangian・Hamiltonianの形で書けていなければなりません。つまりはすべてのファクターを場の形に、かつできれば局所的な場の形に書き直すのが理想です。

そのために、両因子をexpの肩にのせます。すなわち
$$ \int {\cal D}A \exp (iS)=V\int{\cal D}A \ {\rm Det}(M^{ab}(x,y))\delta(\partial A-B)\exp(iS)=V\int{\cal D}A\exp(i\tilde S) $$
のように、新たに生まれた因子を$\tilde S$という形で作用に含めることを試みます。

$\delta (\partial A-B)$に関しては
$$ 1=\int {\cal D}f \exp i\int d^4x\left[-\frac{1}{2\alpha} (f^a(x))^2\right] $$
を用い、これを$Z$にかけ、$\delta(\partial A-B)$の$B$を$f$と同一視し、$f$で汎関数積分します（分配関数は$B$に依存しないことに注意。分配関数は切断の仕方には依存しない。さらに$B$は$\theta$や$A$にも依存していない）。するとデルタ関数の部分は
$$ \exp i\int d^4x \left(-\frac{1}{2\alpha}(\partial_\mu A^{\mu a})^2 \right)$$
になります。

一方$({\rm Det}M^{ab}(x,y))$に関しては
$$ ({\rm Det}M^{ab}(x,y))=\int{\cal D}c{\cal D}\bar c\exp i\int d^4x(i\bar c(x)^aM^{ab}(x,y)c^b(y)) $$
と書けることを用います。ここで$c^a,\bar c^a$はGrassmann数であり、反可換であることに注意してください。この式は、$M$を対角化してガウス積分すると$M$の固有値の積が現れ、これが${\rm Det}(M)$であることから証明できます（大変大雑把ですが...）。$c, \bar c$が普通の数だと、上式左辺が$({\rm Det}(M))^{-1}$になってしまうことに注意してください。

この$c,\bar c$をghost, anti-ghostと呼びます。

最終的に、FPの方法での分配関数は以下のように書けます：

ということで、ゲージ体積をくくりだし、さらに新たに生じた因子を局所場の形で作用に取り込むことに成功しました。

まとめと次回（又はもう少し先）への布石

FPの方法を用いると、ゲージ固定やJacobianがすべてlocalな場の形でLagrangian・Hamiltonianに取り入れられ、摂動論で扱いやすくなりました。かつその構成も直感的にわかりやすく、それほど難しい計算もありません。

しかしながら、ちょっと疑問が残ります。

以前Diracの方法をYang-Mills(YM)理論に適用しました（ ゲージ対称性とは何か(８)：Yang-Mills理論とDiracの方法 参照のこと)。
そこで学んだことに「ゲージ固定は第１種拘束条件の数だけ必要」というのがありました。YMでは第１種拘束条件は2つあり
$$ \pi^{0a}=0, \ D^a_{bi}\pi^{ib}=0 $$
でした。そしてこれらに対応して2つのゲージ固定（たとえば$A^{0a}=0,\ \partial_i A^{ia}=0$）を施しました。

対して、FPの方法を振り返ってみると、

• $D^a_{bi}\pi^{ib}=0$が課されていない
• ゲージ固定が1つしか課されていない ($\partial_\mu A^{\mu a}=B^a$のみ)

ように思えます。

次回は（またはもう少し先）これらの"問題"

を解決したいと思います。

ちなみに結論を言ってしまえば、FPの方法はDiracの方法と無矛盾です。

おしまい。

☆次の記事： ゲージ対称性とは何か(12): Faddeev-Popovの方法とDiracの方法の整合性

Appendix(a): ゲージ体積をくくりだすことの必要性

議論の本質はU(1)ゲージ理論で尽きているので、以下U(1)の議論をします。

(a-1): 分配関数・生成汎関数

多くの素粒子実験では、粒子同士を衝突させ、そこから放出される粒子を調べます。検出器のどの場所に、どんな角度・運動量で、どんな粒子が入ってきたかという情報が大切です。
この情報はいわゆるS行列というもので記述されます。粒子同士の相互作用の切れた場を漸近場といいますが、S行列は、ある時刻$t_I$（すべての粒子の相互作用が切れているとする）におけるある漸近場の状態$\alpha$から、未来のある時刻$t_F$（やはり相互作用は切れているとする）におけるある漸近場の状態$\beta$への遷移振幅のことです：
$$ \begin{align} S_{\beta\alpha}=\langle \beta,t_F|\alpha,t_I\rangle \end{align} $$
通常$t_I,t_F$はそれぞれ$-\infty,+\infty$とします。

以下簡単のためスカラーボソン場$\phi$の系を考えます。
かなり話を省きますが、$S$行列はn点関数
$$ \begin{align} G^{(n)}(x_1,x_2,\ldots,x_n):=\langle \phi(x_1)\phi(x_2)\ldots\phi(x_n)\rangle \end{align} $$
により計算することができます。ここで$\langle {\cal O}(\phi)\rangle$は
$$ \begin{align} \langle{\cal O}(\phi)\rangle&:=\frac{1}{\cal N}\int {\cal D}\phi\ {\cal O}(\phi) \exp(iS),\\ {\cal N}&:=\int {\cal D}\phi\exp(iS) \end{align} $$
のことです。
（$\int {\cal D}\phi$の意味するところはAppendix(b)でお話します）

n点関数は以下の生成汎関数と呼ばれる量
$$ \begin{align} Z[J]:=\frac{1}{\cal N}\int D\phi \exp\left(iS+i\int d^4x J_\mu \phi^\mu\right) \end{align} $$
から、これを外場$J$で汎関数微分することで計算できます。次の式
$$ \begin{align} \langle \phi(x_1)\phi(x_2)\ldots \phi(x_n)\rangle=\left.\frac{\delta}{\delta J(x_1)}\frac{\delta}{\delta J(x_2)}\ldots \frac{\delta}{\delta J(x_n)}Z[J]\right|_{J=0} \end{align} $$
はすぐに確認できます。

上記の${\cal N}$
$$ \int {\cal D}\phi\exp(iS) $$
は分配関数と呼ばれます。これは、無限の過去で真空だった状態が、無限の未来で真空になる遷移振幅です。

(a-2): U(1)ゲージ理論における生成汎関数とその問題点

場の量子論は本来はMinkowski空間における話なのですが、一方取り扱いが（比較的）正確にできるEuclid空間で議論することもよくあります。このパート(a-2)ではEuclid空間で議論します（Appendix(b)ではまたMinkowskiに戻ります）。

U(1)ゲージ理論の生成汎関数を計算します。
これは
$$ \begin{align} Z[J]=\frac{1}{N}\int DA\exp\left[-\int d^4x (\frac{1}{4}F_{\mu\nu} F^{\mu\nu}-J_\mu A^\mu)\right] \end{align} $$
と書けます。
ここで
$$ M_{\mu\nu}=(\partial_\mu\partial_\nu -\partial^2\delta_{\mu\nu}) $$
とします。
$$ \begin{align} -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}+J_\mu A^\mu =-\frac{1}{2}(A_\mu-J_\nu (M^{-1})^\nu_\mu)M^{\mu\rho}(A_\rho-(M^{-1})^\sigma_\rho J_\sigma)+\frac{1}{2}J_\mu(M^{-1})^{\mu\nu}J_\nu \end{align} $$
のように$\exp$の肩を平方完成し、$A\rightarrow \tilde A=A-J(M^{-1})$と変数変換すれば、経路積分を実行できて
$$ \begin{align} Z[J]=\frac{1}{N}({\rm Det}(M))^{-1}\exp(\int d^4x \frac{1}{2}J_\mu(M^{-1})^{\mu\nu}J_\nu) \end{align} $$
となります。

しかしこの表式には問題があります。なぜなら$M$がゼロ固有ベクトル
$$ \begin{align} M_{\mu\nu}\partial^\nu \theta=(\partial_\mu\partial_\nu -\partial^2\delta_{\mu\nu})\partial^\nu\theta=0 \end{align} $$
（$\theta$は任意関数）を持つので、${\rm Det} (M)=0$であり、逆がとれないからです。

このゼロ固有ベクトルの由来は、
$$ M_{\mu\nu}A^\nu $$
にゲージ変換を施すと
$$ M_{\mu\nu}(A^\nu-\frac{i}{e}\partial^\nu\theta)=M_{\mu\nu}A^\nu $$
となり不変になることによります。
つまりはゲージ変換の方向への汎関数積分がゼロ固有値の由来です。

これを避けるには、FPの方法のように、ゲージ固定を行い、ゲージ変換の積分をisolateさせることが必要です。

Appendix(b): 場の量子論における経路積分の直感的理解

ゲージ理論におけるn点関数

$$ \langle A^a_\mu(x_1)A^b_\nu(x_2)\ldots A^e_\lambda(x_n)\rangle=\frac{1}{\cal N}\int {\cal D}A \ A^a_\mu(x_1)A^b_\nu(x_2)\ldots A^e_\lambda(x_n) \exp(iS) $$

が何を意味するか以下見ていきます。

この表式の右辺の積分は
$$\int {\cal D}A=\int \prod_x\prod_\mu\prod_a dA^{a\mu}(x)$$
のことです。$dA^a_\mu(x)$は各$x,a,\mu$における$A^a_\mu(x)$の通常の積分測度です。これはつまりは$A^a_\mu(x)$の汎関数積分です。

汎関数積分を直感的に理解するには、汎関数の空間を離散化するのがいいです。まず、連続的な時空点$x=(t,\vec x)$を離散化します。また$A$の値域も離散化します。そのうえで、時空および$A$の値域を有限区間に限れば、汎関数空間の自由度が有限になります。このようにして有限になった$A$の配位の集合を$\{A\}$とすると、経路積分は
$$ \int {\cal D}A\xrightarrow{離散化}\sum_{\{A\}} $$
と書けます。つまりは「可能な$A$の配位で和を取れ」というのが汎関数積分の意味です。
この議論は数学的には非常にいいかげんだと思うのですが、ご容赦ください。

改めて上記のn点関数が何かということを考えてみると

です。 これは言い換えると

とも言えます。ただし、$\exp(iS(A))$は絶対値1の複素数であって($S(A)$はふつうは実数)、確率とは解釈できないですが、類似性があります。ちなみに、Minkowski空間からEuclid空間に移ると
$$\exp(iS)\xrightarrow{Euclid化}\exp(-S_E) \ \ (S_E\ge 0)$$
と書くことができて、$\langle {\cal O} \rangle$は本当の期待値と解釈できます（特殊な系では$S_E$が複素数になることがありますが、例外的です）。すなわちEuclid空間での場の量子論は、統計力学系とみなせます。

このように、経路の積分（=汎関数積分、様々な場の配位による和）により、量子力学的な確率を理論に取り込むのが「経路積分法」です。

n点関数の物理的な描像は、ゲージ群のadjointの足およびLorentzの足が$(a,\mu),(b,\nu),\ldots,(e,\lambda)$である光子が、それぞれ$x_1,x_2,\ldots,x_n$で見いだされる確率振幅です（図６）。大きな斜線つきの丸は、可能な任意の相互作用を表します。

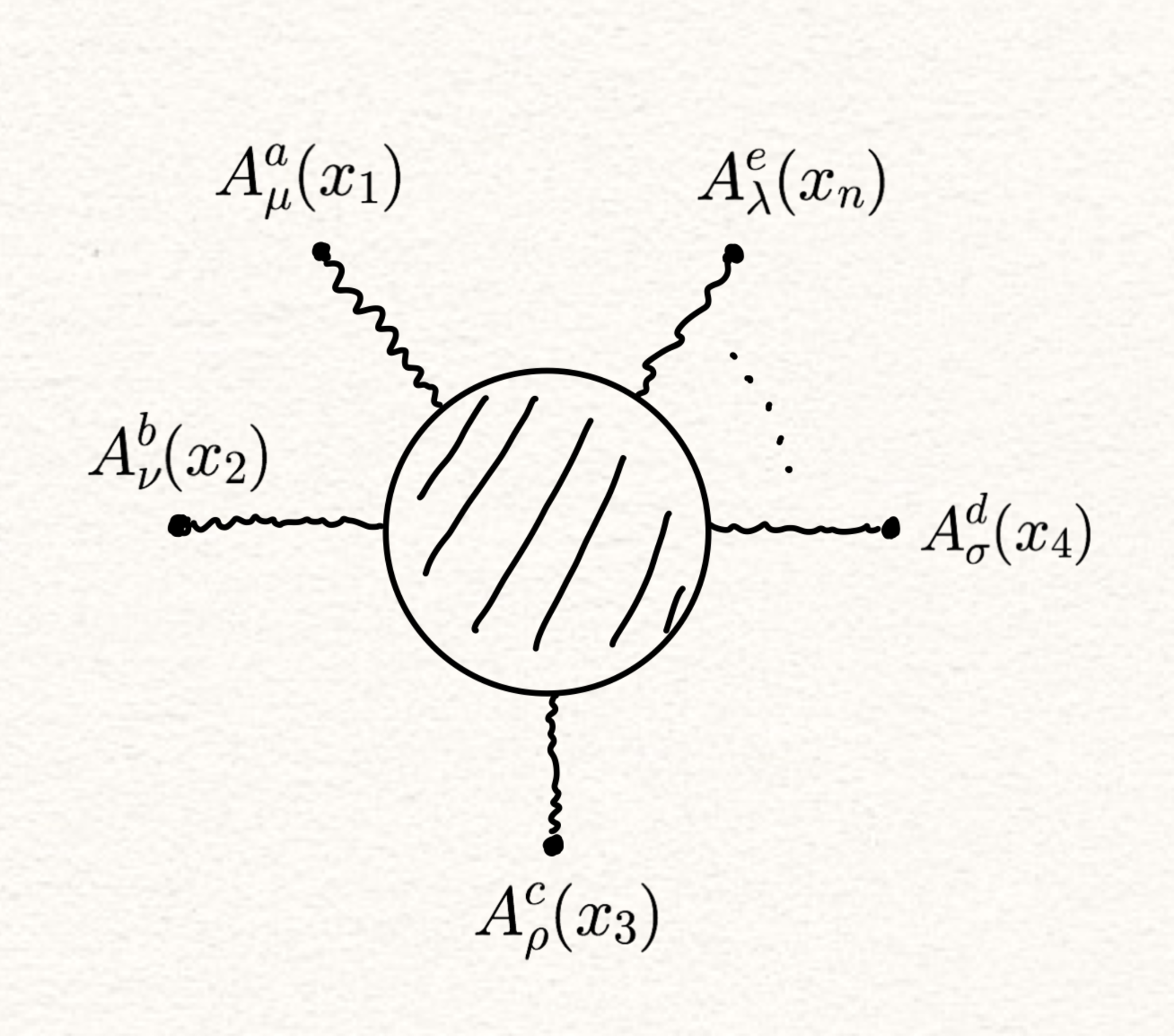n点関数の物理的な描像