Re:パワーな定積分

はじめに

今回は昔計算した次の積分を，前回とは少し異なる方法で積分しようと思います．今回の方が計算量は少なくなると期待していたのですが，結局あまり変わらない気がします．

前回の記事は コチラからどうぞ

解答

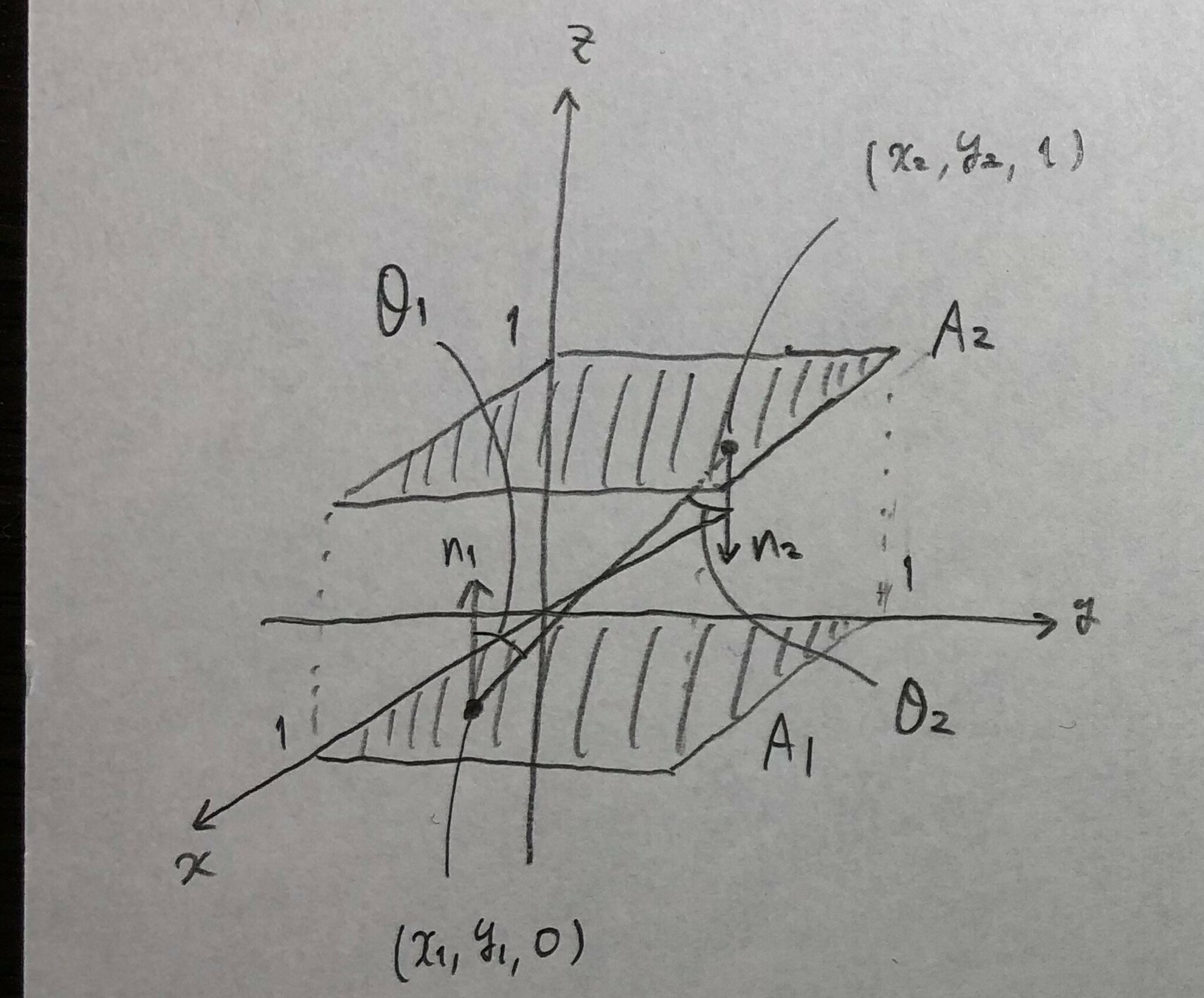唐突な設定

唐突ですが，
$$A_1=\{(x,y,z) \in \mathbb{R}^3 \, | \, 0 \leq x,y \leq 1, \, z=0\}$$
$$A_2=\{(x,y,z) \in \mathbb{R}^3 \, | \, 0 \leq x,y \leq 1, \, z=1\}$$
とし，$A_1,A_2$の面の向き(単位法線ベクトル)はそれぞれ$n_1=(0,0,1), \, n_2=(0,0,-1)$であるとします．また，$A_1$内の点は$(x_1,y_1,0)$という座標で，$A_2$内の点は$(x_2,y_2,1)$という座標で表されるとし，$r=(x_2-x_1, y_2-y_1, 1)$，$S=|r|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+1}$とおきます．すると，内積を用いることで
$$\cos\theta_1=\frac{r \cdot n_1}{|r||n_1|}=\frac{1}{S}$$
$$\cos\theta_2=\frac{(-r) \cdot n_2}{|r||n_2|}=\frac{1}{S}$$
と計算できます．

このとき，
$$\begin{split} \int_{A_1}\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_1dA_2 &= \int_{A_1}\int_{A_2}\frac{1}{S^4}\,dx_1dy_1dx_2dy_2 \\ &= \int_0^1dx_1\int_0^1dy_1\int_0^1dx_2\int_0^1dy_2\,\cfrac{1}{\{(x_2-x_1)^2+(y_2-y_1)^2+1\}^2} \end{split}$$
となるので，最左辺の面積分が求める値です(実は元々最左辺の面積分があって，それを座標によって書き直したものを問題としていました)．以下，この面積分について考えていきます．

$A_2$に関する面積分

またまた唐突ですが，
$$\left\{\begin{array}{l} P=\frac{y_2-y_1}{2S^2} \\ Q=\frac{-(x_2-x_1)}{2S^2} \\ R=0 \\ \end{array}\right.$$
という$x_2,y_2$を変数に持つ3つの関数$P,Q,R$を考えます．すると，実は
$$\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_2=\int_Cv \cdot t\, dC$$
が成り立つことが知られています．ここで，$C$は$A_2$の境界，$v=(P,Q,R)$，$t$は$C$の接ベクトルで，$C$の向きは$A_2$の向きと右手系をなす方向です．特に今回の場合$C$の向きは正方形$A_2$の周を時計回りに周る方向です．これにより，面積分を線積分に変換することができます．まず，この線積分を求めましょう．そのために$C$を次のように分割します．

$C$の分割

さて，$C_1$は$(1-x_2,0,0) \, (0 \leq x_2 \leq 1)$と媒介変数表示されるので，特に$t=(-1,0,0)$です．よって線積分は
$$\begin{split} \int_{C_1}v \cdot t\,dC = \int_0^1(-P|_{y_2=0})\, dx_2 &=\frac{1}{2}\int_0^1\frac{y_1}{(x_2-x_1)^2+y_1^2+1}\, dx_2 \\ &= \frac{y_1}{2}\left[\frac{1}{\sqrt{y_1^2+1}}\,{\rm Arctan}\left( \frac{x_2-x_1}{\sqrt{y_1^2+1}}\right) \right]_0^1 \\ &= \frac{y_1}{2\sqrt{y_1^2+1}}\left\{{\rm Arctan}\left( \frac{1-x_1}{\sqrt{y_1^2+1}}\right)+{\rm Arctan}\left( \frac{x_1}{\sqrt{y_1^2+1}}\right) \right\} \end{split}$$
と計算できます．ここで， コチラの記事 内にある2次多項式の逆数の積分を用いました．

$C_2,C_3,C_4$における線積分も少し値が変わるだけで全く同様にできます．結果は次の通りです．
$$\begin{split} \int_{C_2}v \cdot t\,dC = \int_0^1(Q|_{x_2=0})\, dy_2= \frac{x_1}{2\sqrt{x_1^2+1}}\left\{{\rm Arctan}\left( \frac{1-y_1}{\sqrt{x_1^2+1}}\right)+{\rm Arctan}\left( \frac{y_1}{\sqrt{x_1^2+1}}\right) \right\} \end{split}$$
$$\begin{split} \int_{C_3}v \cdot t\,dC = \int_0^1(P|_{y_2=1})\, dx_2= \frac{1-y_1}{2\sqrt{(1-y_1)^2+1}}\left\{{\rm Arctan}\left( \frac{1-x_1}{\sqrt{(1-y_1)^2+1}}\right)+{\rm Arctan}\left( \frac{x_1}{\sqrt{(1-y_1)^2+1}}\right) \right\} \end{split}$$
$$\begin{split} \int_{C_4}v \cdot t\,dC = \int_0^1(-Q|_{x_2=1})\, dy_2= \frac{1-x_1}{2\sqrt{(1-x_1)^2+1}}\left\{{\rm Arctan}\left( \frac{1-y_1}{\sqrt{(1-x_1)^2+1}}\right)+{\rm Arctan}\left( \frac{y_1}{\sqrt{(1-x_1)^2+1}}\right) \right\} \end{split}$$

これより，$A_2$に関する面積分は次のように計算できます．
$$\begin{split} \int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_2 &= \frac{y_1}{2\sqrt{y_1^2+1}}\left\{{\rm Arctan}\left( \frac{1-x_1}{\sqrt{y_1^2+1}}\right)+{\rm Arctan}\left( \frac{x_1}{\sqrt{y_1^2+1}}\right) \right\}\hspace{0.2in} \cdots \hspace{0.1in} {\rm (i)} \\ &+ \frac{x_1}{2\sqrt{x_1^2+1}}\left\{{\rm Arctan}\left( \frac{1-y_1}{\sqrt{x_1^2+1}}\right)+{\rm Arctan}\left( \frac{y_1}{\sqrt{x_1^2+1}}\right) \right\} \hspace{0.2in} \cdots \hspace{0.1in} {\rm (ii)}\\ &+ \frac{1-y_1}{2\sqrt{(1-y_1)^2+1}}\left\{{\rm Arctan}\left( \frac{1-x_1}{\sqrt{(1-y_1)^2+1}}\right)+{\rm Arctan}\left( \frac{x_1}{\sqrt{(1-y_1)^2+1}}\right) \right\} \hspace{0.2in} \cdots \hspace{0.1in} {\rm (iii)}\\ &+ \frac{1-x_1}{2\sqrt{(1-x_1)^2+1}}\left\{{\rm Arctan}\left( \frac{1-y_1}{\sqrt{(1-x_1)^2+1}}\right)+{\rm Arctan}\left( \frac{y_1}{\sqrt{(1-x_1)^2+1}}\right) \right\} \hspace{0.2in} \cdots \hspace{0.1in} {\rm (iv)} \end{split}$$

$A_1$に関する面積分

ここから先は$A_1$の面積分を普通に逐次積分していきます．関数が多くて大変なように見えますが，どれも似た形をしているので，実は1つ計算すると後は変数変換で同じように計算できます．

まず(i)を$y_1$で積分しましょう．部分積分から
$$\begin{split} \int_0^1\frac{y_1}{\sqrt{y_1^2+1}}{\rm Arctan}\left( \frac{x_1}{\sqrt{y_1^2+1}}\right)dy_1 &= \left[\sqrt{y_1^2+1}{\rm Arctan}\left( \frac{x_1}{\sqrt{y_1^2+1}}\right)\right]_0^1+x_1\int_0^1\frac{y_1}{y_1^2+x_1^2+1}\,dy_1 \\ &= \sqrt{2}{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)-{\rm Arctan}(x_1)+x_1\left[\frac{1}{2}\log(y_1^2+x_1^2+1) \right]_0^1 \\ &= \sqrt{2}{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)-{\rm Arctan}(x_1)+\frac{x_1}{2}\log\frac{x_1^2+2}{x_1^2+1} \end{split}$$
と計算されるので，
$$\begin{split} \int_0^1\frac{y_1}{\sqrt{y_1^2+1}}{\rm Arctan}\left( \frac{1-x_1}{\sqrt{y_1^2+1}}\right)dy_1 = \sqrt{2}{\rm Arctan}\left(\frac{1-x_1}{\sqrt{2}}\right)-{\rm Arctan}(1-x_1)+\frac{1-x_1}{2}\log\frac{(1-x_1)^2+2}{(1-x_1)^2+1} \end{split}$$
も分かります．従って，
$$\begin{split} F(x):=&\sqrt{2}{\rm Arctan}\left(\frac{x}{\sqrt{2}}\right)-{\rm Arctan}(x)+\frac{x}{2}\log\frac{x^2+2}{x^2+1} \\ &+ \sqrt{2}{\rm Arctan}\left(\frac{1-x}{\sqrt{2}}\right)-{\rm Arctan}(1-x)+\frac{1-x}{2}\log\frac{(1-x)^2+2}{(1-x)^2+1} \end{split}$$
とおけば，(i)を$y_1$で積分した結果は$\frac{F(x_1)}{2}$となります．(ii)は(i)の場合と$x_1,y_1$が入れ替わっていることから，(ii)を$x_1$で積分すると$\frac{F(y_1)}{2}$となります．更に，任意の関数$g(x)$に対して等式
$$\int_0^1g(x)\, dx=\int_0^1g(1-x)\,dx$$
が成り立つことから，(iii)を$y_1$で積分すると$\frac{F(x_1)}{2}$を，(iv)を$x_1$で積分すると$\frac{F(y_1)}{2}$を得ることも分かります．従って，次が成り立ちます．
$$\begin{split} &\int_{A_1}\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_1dA_2 \\ &= \frac{1}{2}\left\{\int_0^1F(x_1)\, dx_1+\int_0^1F(y_1)\,dy_1+\int_0^1F(x_1)\, dx_1+\int_0^1F(y_1)\, dy_1\right\} \\ &= 2\int_0^1F(x_1)\,dx_1 \\ &= 2\int_0^1\left\{\sqrt{2}{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)-{\rm Arctan}(x_1)+\frac{x_1}{2}\log\frac{x_1^2+2}{x_1^2+1}\right\}dx_1 \\ &\hspace{0.5in} + 2\int_0^1\left\{\sqrt{2}{\rm Arctan}\left(\frac{1-x_1}{\sqrt{2}}\right)-{\rm Arctan}(1-x_1)+\frac{1-x_1}{2}\log\frac{(1-x_1)^2+2}{(1-x_1)^2+1} \right\}dx_1 \\ &= 4\int_0^1\left\{\sqrt{2}{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)-{\rm Arctan}(x_1)+\frac{x_1}{2}\log\frac{x_1^2+2}{x_1^2+1}\right\}dx_1 \end{split}$$
後は各項を積分するだけです．最初の2項は
$$\int_0^1\sqrt{2}{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)\,dx_1=\left[\sqrt{2}x_1{\rm Arctan}\left(\frac{x_1}{\sqrt{2}}\right)-\log\left(1+\frac{x_1^2}{2}\right) \right]_0^1=\sqrt{2}{\rm Arctan}\left(\frac{1}{\sqrt{2}}\right)-\log\frac{3}{2}$$
$$\int_0^1{\rm Arctan}\left(x_1\right)\,dx_1=\left[x_1{\rm Arctan}\left(x_1\right)-\frac{1}{2}\log\left(1+x_1^2\right) \right]_0^1=\frac{\pi}{4}-\frac{1}{2}\log2$$
と直ぐに求められます．最後の項は，部分積分から
$$\begin{split} \int_0^1x_1\log(x_1^2+1)\, dx &= \left[\frac{x_1^2}{2}\log(x_1^2+1) \right]_0^1-\int_0^1\frac{x_1^3}{x_1^2+1}\, dx_1 \\ &=\frac{1}{2}\log2-\int_0^1\left(x_1-\frac{x_1}{x_1^2+1} \right) dx_1 \\ &= \frac{1}{2}\log2-\frac{1}{2}+\left[\frac{1}{2}\log(x_1^2+1)\right]_0^1 = \log 2-\frac{1}{2} \end{split}$$
$$\begin{split} \int_0^1x_1\log(x_1^2+2)\, dx &= \left[\frac{x_1^2}{2}\log(x_1^2+2) \right]_0^1-\int_0^1\frac{x_1^3}{x_1^2+2}\, dx_1 \\ &=\frac{1}{2}\log3-\int_0^1\left(x_1-\frac{2x_1}{x_1^2+2} \right) dx_1 \\ &= \frac{1}{2}\log3-\frac{1}{2}+\left[\log(x_1^2+2)\right]_0^1 = \frac{3}{2}\log 3-\log2-\frac{1}{2} \end{split}$$
と計算されるので
$$\begin{split} \int_0^1\frac{x_1}{2}\log\frac{x_1^2+2}{x_1^2+1}\, dx_1 &= \frac{1}{2}\int_0^1x_1\log(x_1^2+2)\, dx-\frac{1}{2}\int_0^1x_1\log(x_1^2+1)\, dx \\ &= \frac{3}{4}\log3-\log2 \end{split}$$
となります．以上より，求める値は
$$4\left(\sqrt{2}{\rm Arctan}\left(\frac{1}{\sqrt{2}}\right)-\log\frac{3}{2}-\frac{\pi}{4}+\frac{1}{2}\log2+\frac{3}{4}\log3-\log2\right) = 4\sqrt{2}{\rm Arctan}\left(\frac{1}{\sqrt{2}}\right)+\log\frac{4}{3}-\pi$$
となります．これは 前に求めた値 と一致していますね．

背景とからくり

上で出現した面積分
$$\int_{A_1}\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_1dA_2$$
は，より一般には「形態係数」という値を求める際に立ちはだかります．そして，参考文献[1]では，$A_1$が向きを持った微小面である場合の値，即ち面積分
$$\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_2$$
を線積分に変換する次のような方法が示されています．

ユークリッド空間$\mathbb{R}^3$内で考えます．点$A_1=(x_1,y_1,z_1)$を始点とするベクトル$n_1$を考え，$A_2$は有限の面積$A_2$と向きを持つ曲面とします．但し，点$A_1$は$A_2$上にないとします．$A_2$内の点を$(x_2,y_2,z_2)$という座標で表し，$r=(x_2-x_1,y_2-y_1,z_2-z_1)$とおきます．また，$S=|r|$とおきます．$r$と$n_1$がなす角を$\theta_1$，$A_2$内の点$(x_2,y_2,z_2)$における$A_2$の単位法線ベクトル$n_2$がなす角を$\theta_2$とすると，上でやったように内積を用いることで
$$\cos\theta_1=\frac{r \cdot n_1}{|r||n_1|}=\frac{r \cdot n_1}{S}$$
$$\cos\theta_2=\frac{(-r) \cdot n_2}{|r||n_2|}=-\frac{r \cdot n_2}{S}$$
と計算できます．

このとき次の面積分を考えます．
$$\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_2=\int_{A_2}\frac{r \cdot n_1}{S^4}\,((-r) \cdot n_2)\,dA_2=\int_{A_2}(-fr) \cdot n_2 \, dA_2$$
但し，$f=\frac{r \cdot n_1}{S^4}$とおいています．ここで，$x_2,y_2,z_2$を変数に持つ関数$P,Q,R$を考え，これらを成分に持つベクトル$v$を${\rm rot}\,v=-fr$を満たすように定めることができたとします．即ち，
$$\left\{\begin{array}{l} \frac{\partial R}{\partial y_2}-\frac{\partial Q}{\partial z_2}=(x_1-x_2)f \\ \frac{\partial P}{\partial z_2}-\frac{\partial R}{\partial x_2}=(y_1-y_2)f \\ \frac{\partial Q}{\partial x_2}-\frac{\partial P}{\partial y_2}=(z_1-z_2)f \end{array}\right.$$
を満たすような$x_2,y_2,z_2$の関数$P,Q,R$が見つかったとします．すると，ストークスの定理から
$$\int_{A_2}\frac{\cos\theta_1\cos\theta_2}{S^2}\,dA_2=\int_{A_2}(-fr) \cdot n_2 \, dA_2=\int_{C}v \cdot t\, dC$$
が成り立ちます．ここで$C$は$A_2$の境界であり，その向きは$A_2$の向きと右手系をなすように定められているとします．また，$t$は$C$の接ベクトルを表します．これにより面積分を線積分に変換することができます．

ただ，そのためには上の関係を満たす$P,Q,R$を探さなければなりません．参考文献[1]には，そのような$P,Q,R$として次の形のものが示されていました．ここで$n_1=(\alpha_1,\beta_1,\gamma_1)$とおいています．
$$\left\{\begin{array}{l} P=\frac{-\beta_1(z_2-z_1)+\gamma_1(y_2-y_1)}{2S^2} \\ Q=\frac{\alpha_1(z_2-z_1)-\gamma_1(x_2-x_1)}{2S^2} \\ R=\frac{-\alpha_1(y_2-y_1)+\beta_1(x_2-x_1)}{2S^2} \\ \end{array}\right.$$
これらを上の偏微分方程式から求める方法は載っていなかった(し，自分でも思いつかない)ので分かりませんが，これらがその偏微分方程式を満たすことは計算すれば分かります．

上の計算で唐突に姿を現した$P,Q,R$は，この事実から計算されていたのです．

さいごに

面積分より線積分の方が楽だろうと思っていたのですが，積分する項が増えてしまったので見た目の作業量に変化は無い気がしますね．線積分に変換する恩恵をもっと受けられる面積分を考えていきたいです．

今回の記事は以上です．
お読み頂きありがとうございました．