走る結合定数の計算(1/5): くりこみ概論
★ 本記事では、以下の規約を採用します（4次元の場合）：
- 自然単位系を用いる：$c=\hbar=1$
- $\mu,\nu,\rho,\sigma$等ギリシャ文字はLorentzの足で、$0$から$3$をとる。$0$が時間成分、$1$-$3$は空間成分
- $(x^0,x^1,x^2,x^3)=(t,x,y,z)$、$(\partial_0,\partial_1,\partial_2,\partial_3)=(\partial/\partial t,\partial/\partial x,\partial/\partial y, \partial/\partial z)$、$(p^0,p^1,p^2,p^3)=(E,p_x,p_y,p_z)$ ($E$: エネルギー、$p_x,p_y,p_z$: 運動量の$x,y,z$成分)とする。
- 繰り返した記号は和をとるルール、いわゆるEinsteinの規約を採用する。例えば$A^\mu B_\mu=\sum_{\mu=0}^3 A^\mu B_\mu$である。
- metricは$g_{\mu\nu}:={\rm diag}(1,-1,-1,-1)$とする。Lorentzの足の上げ下げはこれで行う。例えば$A^\mu=g^{\mu\nu}A_\nu$
- 運動量$p^\mu$に対し、$p^2$は次のように定義される：
\begin{align} p^2&:=p^\mu p_\mu=({p^0})^2-({p^1})^2-({p^2})^2-({p^3})^2=E^2-p_x^2-p_y^2-p_z^2 \end{align}
走る結合定数の計算
これから5回の記事で、Yang-Mills(YM)理論の漸近的自由性の証明:「連続極限・次元正則化・minimal subtraction schemeにおいて、YM理論の走る結合定数$g_r(\mu)$を求め、$g_r(\mu\rightarrow \infty)=0$を示す」に関して述べようと思います。
こちらの記事 では、YM理論において、格子正則化での格子間隔$a$に対する裸の結合定数$g_0(a)$を計算しました。そして$\lim_{a\rightarrow 0}g_0(a)=0$であることを見ました。これはYM理論が漸近的自由であることを意味します。ただ、これはスタンダードな漸近的自由性の証明ではありません。また$g_0(a)$を得るのに必要なクォーク間ポテンシャルの計算はせず、文献から引用しました。さらに、くりこまれた結合定数のrunning$g_r(\mu)$（$\mu$はthree gluon vertexに入り込む典型的なエネルギースケール）は導きませんでした（ただし$g_0(a)$と$g_r(\mu)$は結合定数のleading orderでは等しくなることが示せます（Ref.[1]P88-90））。そこで、スタンダードな漸近的自由性の証明を述べておくことにしました。
本記事では、くりこみの概要の説明のため、スカラー場を例にとり、くりこみに至る道筋を非常に簡単に述べます。次回はYM理論におけるくりこみ定数の決定、および走る結合定数の計算に関して述べます。3回目は計算に必要な数学の公式を導入し、4回目でYM理論における具体的なダイアグラムの計算を行います。5回目で走る結合定数を計算して漸近的自由性に関し議論し、終わりにしたいと思います。
本記事は主にRef.[2][3]を元に書かれています。後に説明するGreen関数の位相やファインマン則の規約はRef.[2]に基づきます。
ちなみに、第1回目の本記事を飛ばして2回目から読んでも、YM理論のくりこみ・走る結合定数の計算はできるようにしてあります。
スカラー場におけるくりこみの概要
スカラー場$\phi$の理論
\begin{align} {\cal L}=\frac{1}{2}\partial_\mu \phi\partial^\mu\phi -\frac{1}{2}m^2\phi^2 +{\cal L}_{\rm int}(\phi) \end{align}
を例にとり、$n$点Green関数・摂動論・くりこみの概要を簡単に述べます。スカラー場以外の場が入っていても、以下の議論は同様です。
$n$点Green関数
次の$J(x)$の汎関数を考えます：
\begin{align}
Z[J]=\int {\cal D}\phi
\left.\exp\left(
i\int d^4x {\cal L}+i\int d^4x J(x)\phi(x)
\right)\right/\int {\cal D}\phi
\exp\left(
i\int d^4x {\cal L}
\right)
\end{align}
$J(x)$は場$\phi$に対するsource functionと呼ばれる量です。
$Z(J)$に関して、以下が成立します。
$Z$を$J(x), J(y)$で汎関数微分し、$J=0$とした量
$$
\left.\frac{\delta Z[J]}{\delta J(x) \delta J(y)}\right|_{J=0}
$$
は、$\phi$の場が表す粒子が$y$から$x$まで伝播する確率振幅$^{(*)}$$(i)^2\langle 0|T\hat\phi(x)\hat\phi(y)|0\rangle$に等しい：
$$
\langle 0|T\hat\phi(x)\hat\phi(y)|0\rangle
=(-i)^2\left.\frac{\delta Z[J]}{\delta J(x) \delta J(y)}\right|_{J=0}
$$
ここで$|0\rangle$は理論の真空状態、$\hat \phi$は正準量子化で量子化された場の演算子、$T$はtime-orderd productと呼ばれ、時間が大きい順に演算子を左から並べる演算子である。例えば2つの演算子の場合、以下のようになる：
\begin{align}
T\hat\phi(x)\hat\phi(y)
=
\begin{cases}
\hat\phi(x)\hat\phi(y) & x_0>y_0\\
\hat\phi(y)\hat\phi(x) & y_0>x_0
\end{cases}
\end{align}
$\hat\phi(x)$は状態に作用して、粒子を1つ作る、または消す演算子ですが、ここでは説明は省きます。$\langle 0|T\hat\phi(x)\hat\phi(y)|0\rangle$はFeynman propagatorと呼ばれます。
一般に$J(x_1),J(x_2),\cdots,J(x_n)$で$Z[J]$を微分した量は、粒子$\phi$が$x_1,x_2,\cdots ,x_n$に伝播する確率振幅と等しいです。すなわち以下が成立します：
$$
\langle 0|T\hat\phi(x_1)\hat\phi(x_{2})\cdots \hat\phi(x_{n})|0\rangle
=
(-i)^n\left.\frac{\delta Z[J]}{\delta J(x_1) \delta J(x_2)\cdots \delta J(x_n)}\right|_{J=0}
$$
左辺を$n$点Green関数$G^{(n)}(x_1\cdots x_m)$と呼ぶ。これはまた$Z[J]$が以下のように書けることを意味する：
\begin{align}
Z[J]=\sum_{n=0}^\infty \frac{i^n}{n!}\int d^4x_1 \cdots d^4 x_n J(x_1)\cdots J(x_n) G^{(n)}(x_1\cdots x_n)
\end{align}
場の量子論では、この$G^{(n)}(x_1\cdots x_n)$を計算することが主な作業になります。
摂動論
しかしながら、$n$点Green関数の計算を近似無しで実行するのは一般には不可能です。そこで
摂動論 ＝ 理論の結合定数$g$の展開の次数ごとに計算する手法
を使います。
次のような期待値の記号$\langle\cdots\rangle_0$を導入します：
\begin{align}
\exp
\left[
\frac{1}{2}\frac{\delta}{\delta\phi}\cdot\Delta_F\frac{\delta}{\delta\phi}
\right]
F[\phi]
:=\langle F[\phi]\rangle_0
\end{align}
ここで$F[\phi]$は$\phi$の任意の関数、$\Delta_F$は自由場の2点Green関数、すなわち$i(\partial^2_x+m^2)\Delta_F(x-y)=\delta^4(x-y)$の解です。これは自由粒子が$x$から$y$まで伝播する確率振幅を表します。
このとき次が成立します：
$Z[J]$は次のように表せる：
\begin{align}
Z[J]
=
\sum_{m=0}^\infty
\frac{1}{m!}
\int \left. d^4y_1\cdots d^4y_m
\langle
i{\cal L}_{\rm int}(y_1)\cdots i{\cal L}_{\rm int}(y_m)
e^{iJ\cdot \phi}
\rangle_0
\right/(\text{denominator}). \tag{1}
\end{align}
ここで${\cal L}_{\rm int}$はLagrangianの相互作用項を表す。また$J\cdot \phi:=\int d^4x J(x)\phi(x)$。denominatorはある定数。
$n$点関数を計算したいなら、Eq.(1)において、$e^{iJ\cdot \phi}$を展開し、$J\cdot \phi$の$n$次の項をとってきます。$m$次の摂動では、この${\cal L}_{\rm int}$を$m$個までとってきて、上記計算を行います。${\cal L}_{\rm int}$には結合定数$g$が含まれているので、これはすなわち$g$による展開です。すると$n$点Green関数を摂動で計算することは、以下のような期待値の計算に還元されます：
$$
J(x_1)J(x_2)\cdots J(x_n)\int d^4y_1\cdots \int d^4y_m\langle \phi(x_1)\phi(x_2)\cdots\phi(x_n)\phi(y_1)\phi(y_2)\cdots\phi(y_m)\rangle_0
$$
$\langle\cdots\rangle_0$の計算は、例えば以下のようになります：
\begin{align}
\langle \phi(x_1)\phi(x_2)\rangle_0
&=
\Delta_F(x_1-x_2),\\
\langle\phi(x_1)\phi(x_2)\phi(x_3)\phi(x_4)\rangle_0
&=\Delta_F(x_1-x_2)\Delta_F(x_3-x_4)
+\Delta_F(x_1-x_3)\Delta_F(x_2-x_4)+\Delta_F(x_1-x_4)\Delta_F(x_2-x_3)
\end{align}
容易に想像がつくように、これは、$\phi$のペアを作りそれらを$\Delta_F$にして、これをすべての可能なペアに関して足し合わせたものになっています。わかりやすく記せば以下のようになります：
\begin{align}
\langle\phi(x_1)\phi(x_2)\phi(x_3)\phi(x_4)\rangle_0
&=\phi^A(x_1)\phi^A(x_2)\phi^B(x_3)\phi^B(x_4)
+\phi^A(x_1)\phi^B(x_2)\phi^A(x_3)\phi^B(x_4)
+\phi^A(x_1)\phi^B(x_2)\phi^B(x_3)\phi^A(x_4)\\
&=\Delta_F(x_1-x_2)\Delta_F(x_3-x_4)
+\Delta_F(x_1-x_3)\Delta_F(x_2-x_4)+\Delta_F(x_1-x_4)\Delta_F(x_2-x_3)
\end{align}
$\phi$の上につけた$A,B$は、どの$\phi$がペアになるかを表しています。
ファインマン・ダイアグラム、ファインマン則
$\langle\cdots\rangle_0$の計算をルール化し、さらにダイアグラムを用いてわかりやすく計算する方法が、ファインマン・ダイアグラムを用いた計算法です。
粒子の伝播を表す$\Delta_F$に対応するダイアグラムは線で表します。相互作用項は同じ点の場がいくつかかかるので、その点で$\Delta_F$が接点を持ちます。この接点はバーテックス（＝頂点）と呼ばれます。さらに、ダイアグラムによっては、プロパゲータやバーテックスの「区別のつかなさ」に由来する「対称因子」と呼ばれる数をかける必要があります。このような考察に基づき作られたダイアグラムと式の対応をファインマン則と呼びます。$\Delta_F$は運動量空間で対角化され単純になるため、ファインマン則は基本的には運動量空間で作り、計算を行います。
例えば、$\phi^3$理論:$\displaystyle {\cal L}_{\rm int}=\frac{g}{3!}\phi^3(x)$では、ファインマン則は図1のようになります：
![!FORMULA[109][1668353750][0]理論のファインマン則（Ref.[2]より）。バーテックスには運動量保存則を課す。一番右側の図は「ループをなすダイアグラムの運動量は積分する」ことを意味する。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220726142601.png?alt=media)
$\phi^3$理論のファインマン則（Ref.[2]より）。バーテックスには運動量保存則を課す。一番右側の図は「ループをなすダイアグラムの運動量は積分する」ことを意味する。
各ダイアグラムには青色の式が付随します。$k$は粒子の4元の運動量です。これはよく使われるファインマン則とは$i$の付き方が違うのですが、ダイアグラムを評価する際の$i$の数が少なくなるなど利点があります（Ref.[2]P81）。また、このルールから計算される量は、Green関数に$-i$がかかったものになります。
$n$点Green関数を計算したければ、パーツとなる絵を組み合わせて外線（外に出ている線）が$n$本のダイアグラムを描き、可能なものを全て足し合わせます（トポロジカルに同じダイアグラムは同一視します）。このようにして作ったダイアグラムに対応する式を評価することで、グラフィカルに$n$点Green関数を計算することができます。
具体的に、例えば2点Green関数を計算するなら、以下のようなダイアグラムを評価します：
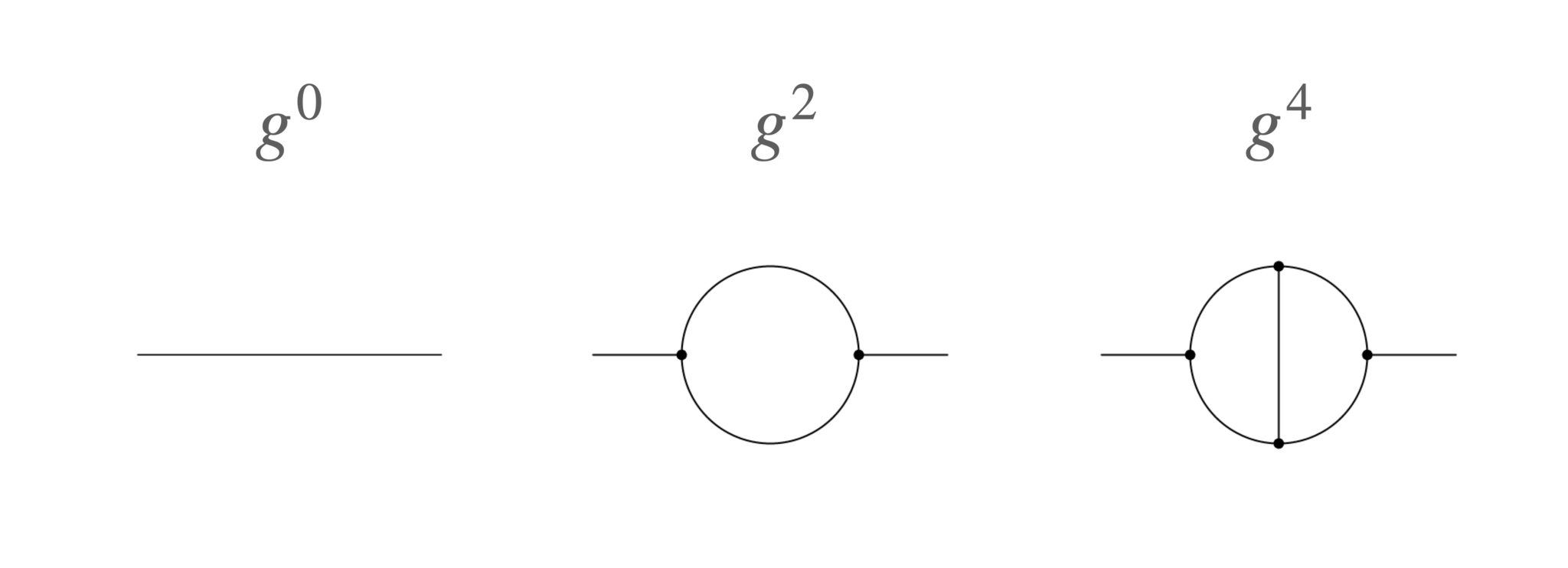2点Green関数に寄与する低次のファインマン・ダイアグラムの例
左から、$g^0, g^2, g^4$のオーダーのダイアグラムの例です。摂動論では$g$の次数の小さい順にその効果をとりこみます。
連結Green関数および1PI頂点関数
$Z(J)$の定義の分母denominatorは、真空泡グラフ（図3）と呼ばれる$J$につながらないグラフを差っ引く効果があります。よって$Z(J)$は真空泡グラフ以外の可能なダイアグラムをすべて含みます。
![真空泡グラフの例。バツ印は!FORMULA[122][36926][0]の存在する点。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220725143758.png?alt=media)
真空泡グラフの例。バツ印は$J$の存在する点。
一方で、次のように定義される$W(J)$は、連結したGreen関数$G^{(n)}_{\rm conn}$の生成汎関数になります（証明は省略します）：
以下で定義される$W(J)$は連結Green関数$G^{(n)}_{\rm conn}$の生成汎関数である：
$$
Z(J)=e^{iW(J)},\\
iW(J)
=
\sum_{n=1}^\infty
\frac{i^n}{n!}
\int d^4x_1\cdots d^4x_n
J(x_1)\cdots J(x_n)
G^{(n)}_{\rm conn}(x_1\cdots x_n)
$$
さらに$W(J)$を$\varphi$に関してLegendre変換した$\Gamma(\varphi)$,
$$ \displaystyle \Gamma(\varphi)=W(J)-J\cdot \varphi,\\ \displaystyle \varphi(x)=\frac{\delta}{\delta J(x)}W(J) =\frac{ \langle 0 |T\hat\phi(x)\exp(iJ\cdot\hat\phi)|0\rangle } { \langle 0|T\exp(iJ\cdot\hat\phi)|0\rangle } $$
は、1粒子既約（one particle irreducible, 1PI）なダイアグラムから外線をもぎとったダイアグラム$\Gamma^{(n)}(x_1\cdots x_n)$（これを1PI頂点関数と呼びます）の生成汎関数になります（これも証明しません）：
上で定義された$\Gamma(\varphi)$は1PI頂点関数の生成汎関数である：
\begin{align}
\Gamma(\varphi)
=
\sum_{n=0}^\infty
\frac{-i}{n!}
\int d^4x_1\cdots d^4x_n
\varphi(x_1)\cdots \varphi(x_n)
\Gamma^{(n)}(x_1\cdots x_n)
\end{align}
ここで1PIとは、内線（外線ではない線）を1つ切っても分離しないダイアグラムのことです。
順番は前後しますが、この後説明する「くりこみ」では、1PI頂点関数$\Gamma^{(n)}(x_1\cdots x_n)$さえくりこんでおけば、すべての発散を取り除けます。例えば$g^2$のオーダーにおける2点Green関数のくりこみなら、図4の2点1PI頂点関数のみ計算すればよいです。
![!FORMULA[137][36407149][0]のオーダーの2点1PI頂点関数。外に伸びるプロパゲータは含まず、黒点で示したバーテックス因子は含むとする。](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220725191531.png?alt=media)
$g^2$のオーダーの2点1PI頂点関数。外に伸びるプロパゲータは含まず、黒点で示したバーテックス因子は含むとする。
くりこみ
ダイアグラムには、粒子の生成・消滅による量子補正に由来する発散が存在するものがあります。これを以下のように処理して、Green関数を有限にします。一連の作業を「くりこみ」と呼びます。
$i\epsilon$処方、Euclid化、正則化
例として図4を計算します。このダイアグラムに対応する式は以下です：
$$
\frac{g^2}{2}\int \frac{d^4k}{(2\pi)^4i}
\frac{1}{m^2-k^2}\frac{1}{m^2-(k+p)^2}
$$
ここで1/2のファクターは対称因子であり、外線の運動量を$p$、内線で積分される運動量を$k$としました。
この積分はこのままではill-definedなので、以下のような変更をします：
- $i\epsilon$処方： poleが積分路上に存在することを避けるため、$1/(m^2-k^2)$と$1/(m^2-(k+p)^2)$の分母に$-i\epsilon$を足しておきます（これにより、Green関数はtime-ordered productになります$^{(**)}$）。
- Euclid化： 被積分関数の解析性を使い、$k^0$の積分を純虚数の積分に変えることでMinkowskiからEuclidに移ります（詳しくは一連の記事の第３回、またはweb上の資料や教科書をご参照下さい）。
こうしておいて、4次元の極座標表示に変数変換すると、運動量が大きいとき、$\int dk_E \ 1/k_E$（$k_E$はEuclid空間での運動量の大きさ）の積分になり、発散することがわかります。
正則化
これをとりあえず有限にしておくため、正則化という作業をします。正則化にはいくつか方法があるのですが、わかりやすいのは、運動量の積分の上限を$\Lambda$とすることでカットオフを設けるものです。しかしゲージ理論では、ゲージ対称性及び様々な対称性を保つ正則化である「次元正則化」が有用です。これは、$d$次元を$D=d-2\epsilon$次元（$\epsilon$は複素数の微小パラメータ。プロパゲータの分母の$i\epsilon$とは関係ない）にずらす正則化です。YM理論の場合、現実の$d=4$から次元をずらすと、発散が有限になります。YM理論は4次元でいわゆる「くりこみ可能」（くりこみ不可能でもなければ、超くりこみ可能でもないという意味で）$^{(***)}$です。一方、$\phi^3$理論では6次元がくりこみ可能な次元なので、6次元で考えることも多いです。
ダイアグラムを次元正則化で計算し、$\epsilon$でLaurent展開すると
$$ (\text{term proportional to } 1/\epsilon)+(\text{finite part}) $$
のようになります。$1/\epsilon$に比例する項は$\epsilon\rightarrow 0$で発散します。この項以外は$\epsilon\rightarrow 0$で有限になる項です。高次のダイアグラムを計算すると$1/\epsilon^2$またはそれ以上強く発散する項もありえますが、一連の記事では発散項は$1/\epsilon$に比例する場合のみ取り扱います。
発散の除去
発散項を以下のように除去します。
ここからは6次元の$\phi^3$理論を考えます(Ref.[2])：
$$
{\cal L}=\frac{1}{2}\partial^\mu\phi\partial_\mu\phi-\frac{1}{2}m^2\phi^2+\frac{g}{3!}\phi^3
$$
6次元で考える理由は、上に述べたように、この次元で$\phi^3$理論がくりこみ可能だからです。
まず
$$
\phi=Z_3^{1/2}\phi_r, g=Z_g g_r, m^2=Z_m m_r^2
$$
とreparametrizeします。$r$の添字のついた量を「くりこまれた量」、$Z$らを「くりこみ定数」と呼びます。
次にLagrangianのrearregementをします。${\cal L}$は以下のように書き換えられます：
\begin{align} {\cal L}&=\frac{1}{2}(\partial^\mu\phi_r\partial_\mu\phi_r -m_r^2\phi_r^2) +\frac{g_r}{3!}\phi_r^3 +\frac{1}{2} [(Z_3-1)\partial^\mu\phi_r\partial_\mu\phi_r -(Z_3Z_m-1)m_r^2\phi_r^2] +(Z_3^{3/2}Z_g-1)\frac{g_r}{3!}\phi_r^3 \\ &={\cal L}_{0r}+{\cal L}_{1r}+{\cal L}_{\rm CT},\\ &\begin{cases} \displaystyle {\cal L}_{0r}:=\frac{1}{2}(\partial^\mu\phi_r\partial_\mu\phi_r -m_r^2\phi_r^2),\\ \displaystyle {\cal L}_{1r}:=\frac{g_r}{3!}\phi_r^3,\\ \displaystyle {\cal L}_{\rm CT}:=\frac{1}{2} [(Z_3-1)\partial^\mu\phi_r\partial_\mu\phi_r -(Z_3Z_m-1)m_r^2\phi_r^2] +(Z_3^{3/2}Z_g-1)\frac{g_r}{3!}\phi_r^3 \end{cases} \end{align}
${\cal L}_{\rm CT}$はcounter termと呼ばれます。
こうしておいて、以下のように発散を取り除きます：
- ファインマン・ダイアグラムの計算を${\cal L}_{0r},{\cal L}_{1r}$で行う
- (1)で生じる発散を、counter termから導かれるダイアグラムで打ち消す。発散が消えるようにくりこみ定数$Z$らを決定し、くりこまれた量や物理量を有限にする。具体的には、発散するダイアグラムに、図5のようなファインマン則に従うダイアグラムを足し、発散を消すようにくりこみ定数を決定する
![!FORMULA[176][1668353750][0]理論のcounter terms](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220725123134.png?alt=media)
$\phi^3$理論のcounter terms
例を示しましょう。図6の左のダイアグラムは上で述べたように発散します。そのため、図6の右側のダイアグラムを足し、$Z$らを、発散を消すように決定します。発散を除去するスキームはいろいろあるのですが、一連の記事では、$1/\epsilon$に比例する項のみを消すスキームである"minimal subtraction (MS) scheme"を用います。
![2点1PI頂点関数の!FORMULA[179][36407149][0]のオーダーにおけるくりこみ](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220725123212.png?alt=media)
2点1PI頂点関数の$g^2$のオーダーにおけるくりこみ
次元正則化で計算すると、左のダイアグラムの発散部分は
$$
\frac{g_0^2}{2(4\pi)^3}\left(
-m_r^2+\frac{p^2}{6}
\right)\frac{1}{\epsilon}, \ \ \ g_r=g_0\mu^{\epsilon}
$$
となります。$p$は外線の運動量です。ここで$\mu$は、次元を6からずらしたことによる次元合わせの任意の定数（質量次元$M^1$）です。ここではこれらは認めてもらうことにします。
図6の右のダイアグラムは$(Z_3Z_m-1)m_r^2-(Z_3-1)p^2$なので、両者の和は
$$
\left(Z_3Z_m-1+\frac{g_0^2}{2(4\pi)^3}\frac{1}{\epsilon}\right)m_r^2
+\left(
-\frac{g_0^2}{2(4\pi)^3}\frac{1}{6}\frac{1}{\epsilon}-(Z_3-1)
\right)p^2
$$
MS schemeでは、発散部分のみ除去するので（${\cal O}(g_0^0)$の1は残しておく）、$g_0^2$のオーダーでは
$$
Z_3Z_m=1-\frac{g_0^2}{2(4\pi)^3}\frac{1}{\epsilon}, \ \ \
Z_3=1-\frac{g_0^2}{12(4\pi)^3}\frac{1}{\epsilon},\\
\therefore Z_m=1-\frac{5g_0^2}{12(4\pi)^3}\frac{1}{\epsilon}+{\cal O}(g_0^4)
$$
となります。
さらに高次のダイアグラムをくりこむ場合は、くりこみ定数を$g$で展開し、高次のダイアグラムが含む低次の部分ダイアグラムの発散を低次のくりこみ定数で消します。そして、残ったダイアグラム全体の発散を高次のくりこみ定数で消します。一連の記事では$g^2$のオーダーでのくりこみしか行わないので、高次のくりこみに関しては説明を省きます。
以上が非常に簡単な、くりこみに至るまでの道筋でした。
まとめ
本記事では、スカラー場において、くりこみに至るお話を簡潔に述べました。ごく簡単にしか説明していませんので、具体的なくりこみの計算に関しては今後のYM理論における記事を参考にしてください。1回目の本記事を読まなくても2回目以降の記事を読めば計算はわかるようにしてあります。
次回はYang−Mills理論におけるくりこみ定数の決定、および走る結合定数の計算に関して述べます。
おしまい。${}_\blacksquare$
$\clubsuit$次の記事： 走る結合定数の計算(2/5): Yang-Mills理論のくりこみ概論
$(*)$ 確率振幅=絶対値を2乗したら確率になる量
$(**)$ $i\epsilon$処方は、経路積分では、無限の過去おける初期状態と無限の未来における終状態への依存性をなくす効果があります(Ref.[3]P90)。
$(***)$ 一般に、発散するダイアグラムが有限個に収まり、発散を除去できる場合を「超くりこみ可能」、発散するダイアグラムは無限個あるが種類は有限個であり、くりこみで発散を除去できる場合を「くりこみ可能」、有限個のcounter termでは発散を除去できない場合を「くりこみ不可能」と呼びます。これらの分類は理論が含む結合定数の質量次元で決まっています。$g$の質量次元を$[g]$で表し、$[g]=-r$とすると以下が成立します：
- $r>0$の結合定数が少なくとも1つあるとき「くり込み不可能」
- すべての結合定数に対し$r\le 0$かつ1つでも$r=0$の結合定数があるとき「くりこみ可能」
- すべての結合定数が$r<0$のとき「超くりこみ可能」
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
