走る結合定数の計算(2/5): Yang-Mills理論のくりこみ概論

場の量子論,くりこみ,ゲージ理論

387

更新履歴

03Aug.2022: 「(A)ファインマン則の導入・くりこみ定数の決定」の2.3.の文章がわかりにくかったため修正しました。
14Aug.2022: タイトルを「Yang-Mills理論のくりこみ」から「Yang-Mills理論のくりこみ概論」に変更しました

★ 本記事は走る結合定数の計算(1/5):くりこみ概論の続きです
★ 以下の規約を用います：

自然単位系を用いる: $c = ℏ = 1$
$μ, ν, ρ, σ$ 等ギリシャ文字はLorentzの足で、 $0$ から $3$ をとる。 $0$ が時間成分、 $1$ - $3$ は空間成分
$a, b, c$ 等のアルファベットはadjoint表現のゲージ群の足。SU(N)のゲージ理論では1から $N^{2} - 1$ をとる。gluonおよびghostのゲージ群の足はこれ。
$i, j$ 等のアルファベットはfundamental表現のゲージ群の足。SU(N)のゲージ理論では1から $N$ をとる。quarkのゲージ群の足はこれ。
$x^{μ} : (x^{0}, x^{1}, x^{2}, x^{3}) = (t, x, y, z)$ とする。
4元運動量は $p^{μ} : (p^{0}, p^{1}, p^{2}, p^{3}) = (E, p_{x}, p_{y}, p_{z})$ ( $E$ : 粒子のエネルギー, $p_{x}, p_{y}, p_{z}$ :運動量の $x, y, z$ 成分）である。
metricは $g_{μ ν} := d i a g (1, - 1, - 1, - 1)$ とする。
繰り返した記号は和をとるルール、いわゆるEinsteinの規約を採用する。
例えば $A^{μ} B_{μ} = \sum_{μ = 0}^{3} A^{μ} B_{μ}$ 、 $C_{a} D_{a} = \sum_{a = 1}^{N^{2} - 1} C_{a} D_{a}$ 、 $E_{i} F_{i} = \sum_{i = 1}^{N} E_{i} F_{i}$ である。Minkowski時空においてLorentzの足 $μ, ν$ 等は上つきと下つきで縮約をとる。ゲージ群の足に関しては上つき・下つきは特に区別はない。
$γ^{μ} (μ = 0, 1, 2, 3)$ は $4 \times 4$ の複素行列であり、Clifford algebraの元である: ${γ^{μ}, γ^{ν}} = 2 g^{μ ν}$ 。これらはDirac行列と呼ばれる。

はじめに

Yang-Mills理論における走る結合定数の計算第２回です。

前回はスカラー場の理論を用いて、ごく簡単にくりこみの概論を説明しました。今回はYang-Mills(YM)理論におけるくりこみの方法、および走る結合定数の計算方法を説明します。ただし、ファインマン則の導出やくりこみを詳しく説明することはせず、その手続きを公理として導入し、計算ができることにのみ特化した説明をします。くりこみとは何かの概要を知りたい方は、前回の記事をご参照ください。具体的なダイアグラムの計算は第４回で行います。

参考文献はRef.[1]です。ファインマン則はこれと同じものを採用しています。

Yang-Mills理論とくりこみ定数

SU(N)のYang-Mills理論のLagrangianは以下です：

$\begin{aligned} (1) & L & = L_{0} + L_{1}, \\ L_{0} & = - \frac{1}{4} (\partial_{μ} A_{ν}^{a} - \partial_{ν} A_{μ}^{a}) (\partial^{μ} {A^{a}}^{ν} - \partial^{ν} {A^{a}}^{μ}) - \frac{1}{2 α} (\partial^{μ} A_{μ}^{a})^{2} + i (\partial^{μ} χ_{1}^{a}) (\partial_{μ} χ_{2}^{a}) + {\bar{ψ}}^{i} (i γ^{μ} \partial_{μ} - m) ψ^{i}, \\ L_{1} & = - \frac{g}{2} f^{a b c} (\partial_{μ} A_{ν}^{a} - \partial_{ν} A_{μ}^{a}) A^{b μ} A^{c ν} - \frac{g^{2}}{4} f^{a b c} f^{c d e} A_{μ}^{a} A_{ν}^{b} A^{c μ} A^{d ν} - i g f^{a b c} (\partial^{μ} χ_{1}^{a}) χ_{2}^{b} A_{μ}^{c} + g {\bar{ψ}}^{i} T_{i j}^{a} γ^{μ} ψ^{j} A_{μ}^{a} \end{aligned}$

$A_{μ}^{a}$ はgluonと呼ばれるゲージ場、 $χ_{1, 2}^{a}$ はghost場、 $ψ^{i}$ はquark場です。 $a, b, c, \dots$ はadjointのゲージ群の足を表し、 $1 \leq a, b, c, \dots \leq N^{2} - 1$ 。 $μ, ν, \dots$ はLorentzの足で、 $0 \leq μ, ν, \dots \leq 3$ です。 $f^{a b c}$ は構造定数と呼ばれる量で、SU(N)の生成子 $T^{a}$ の交換関係 $[T^{a}, T^{b}] = i f^{a b c} T^{c}$ の右辺の係数です。 $f^{a b c}$ は足の入れ替えに関し完全反対称であり、足の上下には意味はなく、 $f_{a b c}$ と書くこともあります。 $α$ はゲージパラメータと呼ばれ、ゲージ固定を指定するパラメータです。

くりこまれた場およびくりこまれた結合定数、ゲージパラメータおよびquark質量を以下のように定義します：
$\begin{aligned} A_{μ}^{a} & = Z_{3}^{1 / 2} A_{r μ}^{a}, χ_{1, 2}^{a} = {\tilde{Z}}_{3}^{1 / 2} χ_{1, 2 r}^{a}, ψ = Z_{2}^{1 / 2} ψ_{r}, \\ g & = Z_{g} g_{r}, α = Z_{3} α_{r}, m = Z_{m} m_{r} \end{aligned}$
$Z$ らはくりこみ定数と呼ばれます。 $r$ のついた量がくりこまれた量、もともとLagrangianに現れる量は裸の量と呼ばれます。

これらのくりこまれた量を用い、Lagrangianを以下の形に変形します：

YM理論のLagrangianをくりこまれた量とcounter termで書き直す

YM理論のLagrangianを以下の形に変形する：
$\begin{array}{r} L = L_{r 0} + L_{r 1} + L_{C} \end{array}$
ここで $L_{r 0}, L_{r 1}$ は、Eq.(1)の $L_{0}, L_{1}$ において、各種の量をくりこまれた量に置き換えたもの。
$L_{C}$ はcounter termと呼ばれ、以下の形をしている：
$\begin{aligned} L_{C} = & (Z_{3} - 1) \frac{1}{2} A_{r}^{a μ} δ_{a b} (g_{μ ν} \partial^{2} - \partial_{μ} \partial_{ν}) A_{r}^{b ν} + ({\tilde{Z}}_{3} - 1) χ_{1 r}^{a} δ_{a b} (- i \partial^{2}) χ_{2 r}^{b} \\ + (Z_{2} - 1) {\bar{ψ}}_{r}^{i} (i γ^{μ} \partial_{μ} - m_{r}) ψ_{r}^{i} - Z_{2} (Z_{m} - 1) m_{r} {\bar{ψ}}_{r}^{i} ψ_{r}^{i} \\ - (Z_{1} - 1) \frac{1}{2} g_{r} f^{a b c} (\partial_{μ} A_{r ν}^{a} - \partial_{ν} A_{r μ}^{a}) A_{r}^{b μ} A_{r}^{c ν} \\ - (Z_{4} - 1) \frac{1}{4} g_{r}^{2} f^{a b e} f^{c d e} A_{r μ}^{a} A_{r ν}^{b} A_{r}^{c μ} A_{r}^{d ν} \\ - ({\tilde{Z}}_{1} - 1) i g_{r} f^{a b c} (\partial^{μ} χ_{1 r}^{a}) χ_{2 r}^{b} A_{r μ}^{c} \\ + (Z_{1 F} - 1) g_{r} {\bar{ψ}}_{r}^{i} T_{i j}^{a} γ^{μ} ψ_{r}^{j} A_{r μ}^{a} \end{aligned}$
ここで $Z_{1}, Z_{4}, {\tilde{Z}}_{1}, Z_{F}$ は
$\begin{array}{r} (2) & Z_{1} := Z_{g} Z_{3}^{3 / 2}, Z_{4} := Z_{g}^{2} Z_{3}^{2}, {\tilde{Z}}_{1} := Z_{g} {\tilde{Z}}_{3} Z_{3}^{1 / 2}, Z_{1 F} = Z_{g} Z_{2} Z_{3}^{1 / 2} \end{array}$
である。

このように、Lagrangianをくりこみに適した形に直しておきます。

くりこみと走る結合定数の計算

一連の記事で行うことは次の(A)(B)です：
(A) ファインマン則を導入する。ダイアグラムを有限にするように、くりこみ定数を決定する
(B) 裸の結合定数が次元正則化で導入されたスケールに依存しないことを要求し、くりこまれた結合定数のrunningを決める

以下(A)(B)について述べます。具体的なダイアグラムの計算は第４回の記事で行います。

(A) ファインマン則の導入・くりこみ定数の決定

まずはファインマン則の導入、およびくりこみ定数の決定法について述べます：

(A)　ファインマン則の導入・くりこみ定数の決定 手順

ファインマン則1
gluon、ghost、quark各粒子の伝播を、以下の線で表現します：
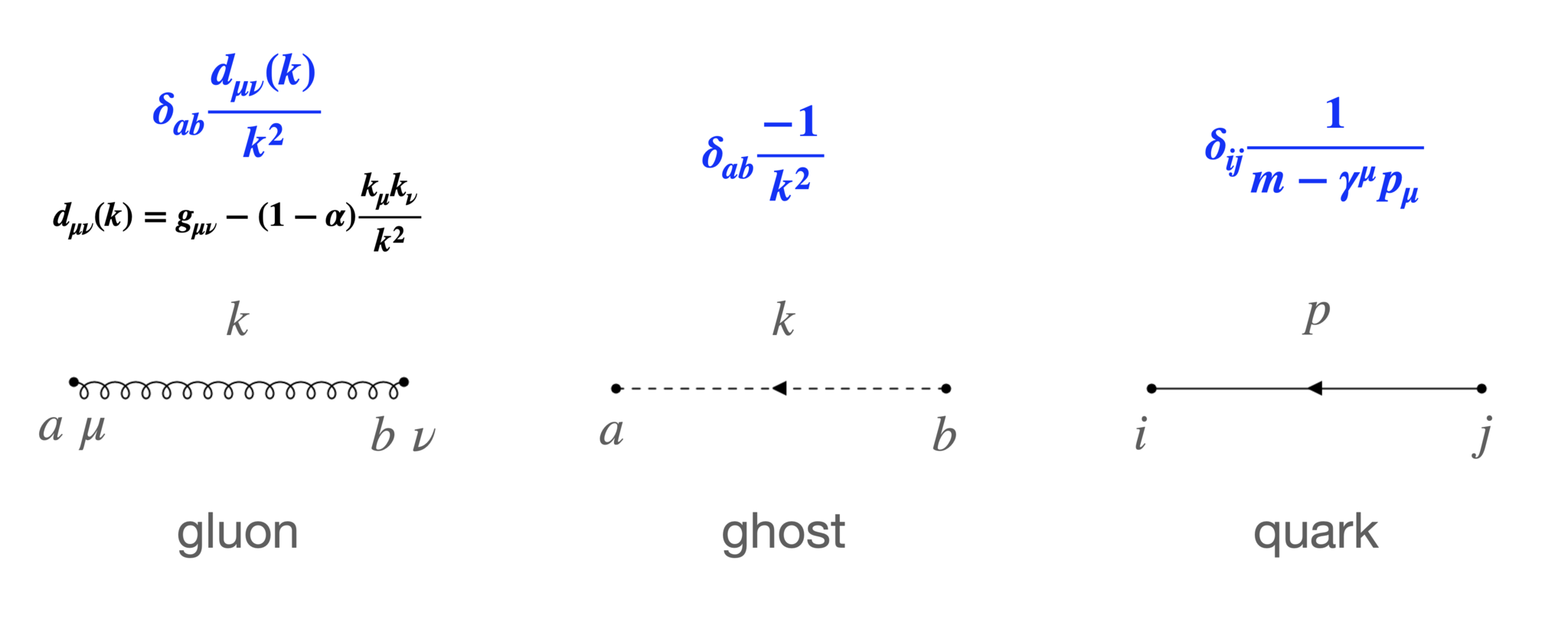$各粒子のpropagator。$\gamma^\mu$はガンマ行列（記事冒頭の規約参照）$ 各粒子のpropagator。 $γ^{μ}$ はガンマ行列（記事冒頭の規約参照）
これらは自由粒子が伝播する際のGreen関数です。これらの線を以下propagatorと呼びます。各propagatorには青色の式が付随します。各線には4元運動量 $k^{μ}$ （quarkは $p^{μ}$ で表記）が付随します。1つの線には1つの運動量が付随します。

さらに粒子は次のような分岐（粒子の生成・消滅）を起こします：

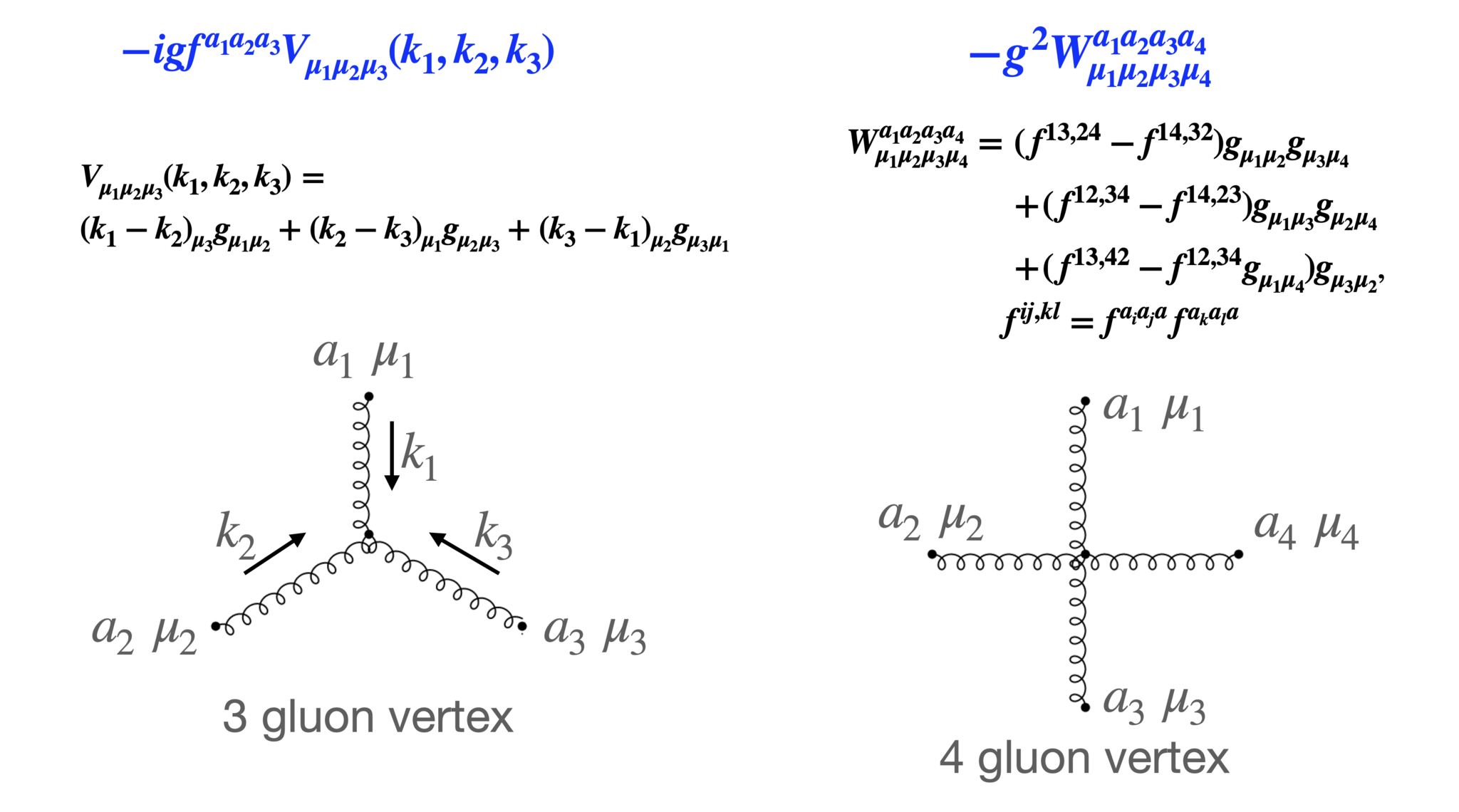
各種vertex
これらの分岐をvertexと呼びます。各vertexには青色の式が付随します。
くりこみでは、全ての可能なダイアグラムを計算する必要はなく、1粒子既約（one particle irreducible (1PI)）頂点関数と呼ばれるダイアグラムを計算すればよいです。
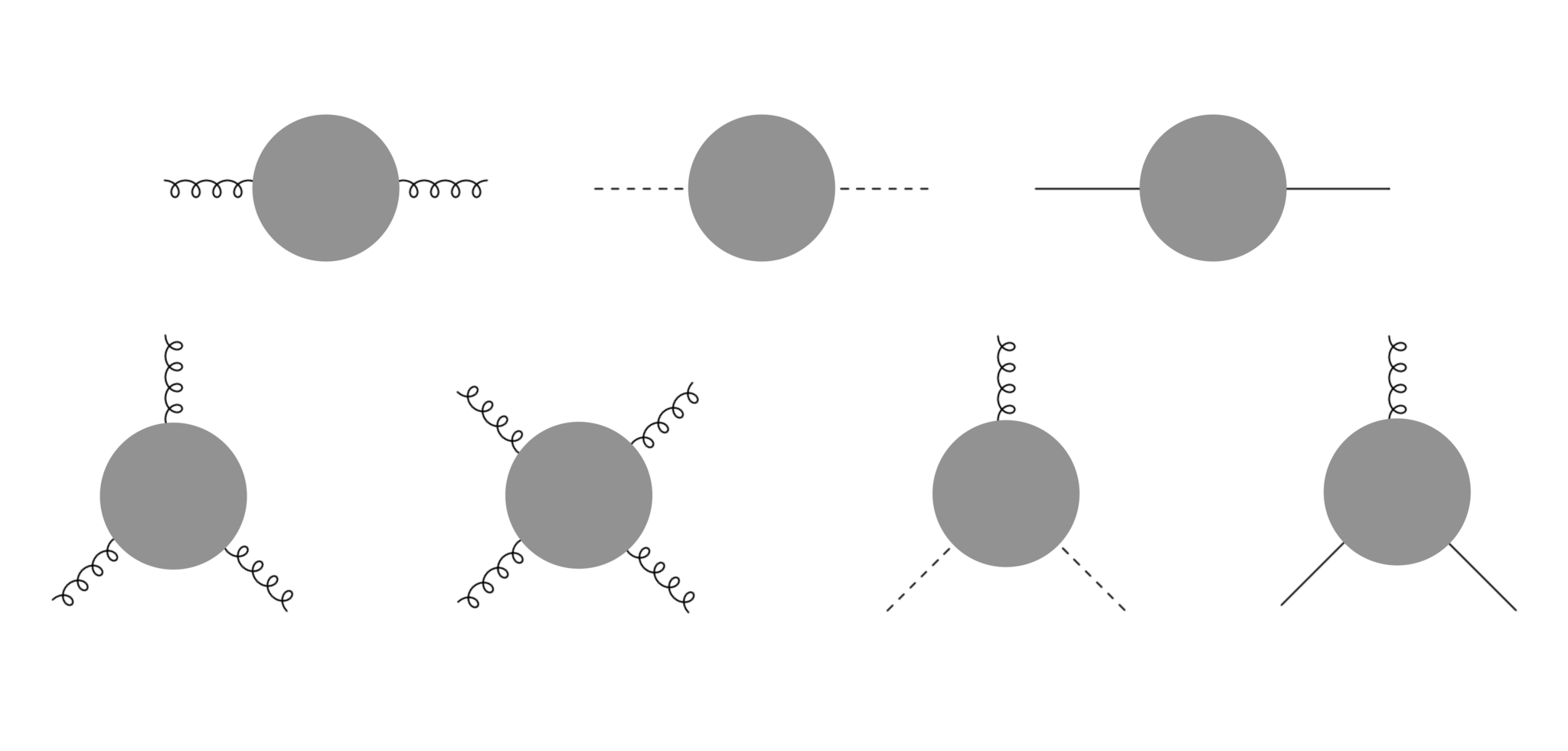くりこみで評価するダイアグラム。これらは1PI頂点関数であり、外に出ているpropagatorは含まないことに注意（vertex因子は含みます）
図3がくりこみで評価する1PI頂点関数です。黒丸は1粒子既約、1PIと呼ばれる一連のダイアグラムであり、「1つの内線を切っても２つの部分に分かれることのないダイアグラム」です。頂点関数では、外に伸びるpropagatorはもぎとり、vertex（および流出入する運動量）のみくっつけます。図3では外にpropagatorが伸びていますが、これは線をつけておかないとどの粒子の伝播を表すかわからないためであり、計算ではvertexだけ残してpropagatorは含めないに注意してください。

図4に1PI頂点関数の例を挙げておきます。緑の線でダイアグラムを切っても２つの部分に分かれないので1PIになっています。
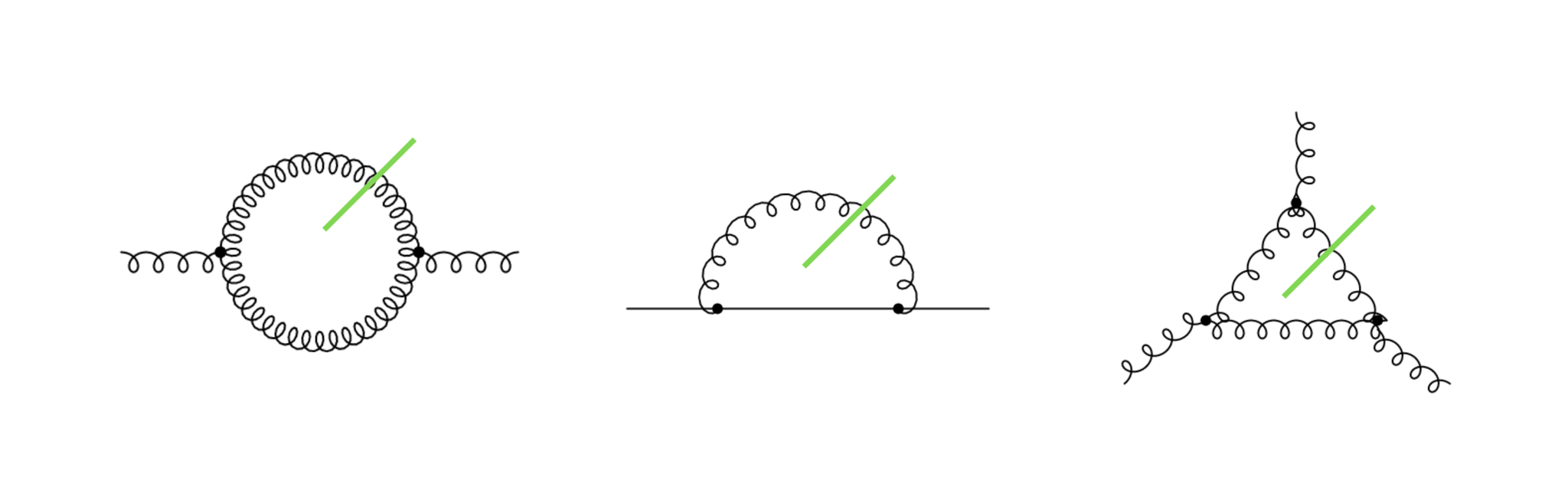図３に示された1PI頂点関数の例。たとえば緑の線で切っても、ダイアグラムが分離することはない。外線のpropagatorは含まない
これらダイアグラムは一般に無限に存在します。そこで結合定数 $g$ による展開を行います。ダイアグラムの結合定数の次数は、そのダイアグラムが含むvertexの数に等しいです。結合定数の $n$ 次のオーダーでは、外線が同じであり、かつ結合定数が $n$ 次のダイアグラム以下のものをすべて足します。例として、ghostの2点1PI頂点関数の $g^{2}$ および $g^{4}$ のダイアグラムを図4に示します:

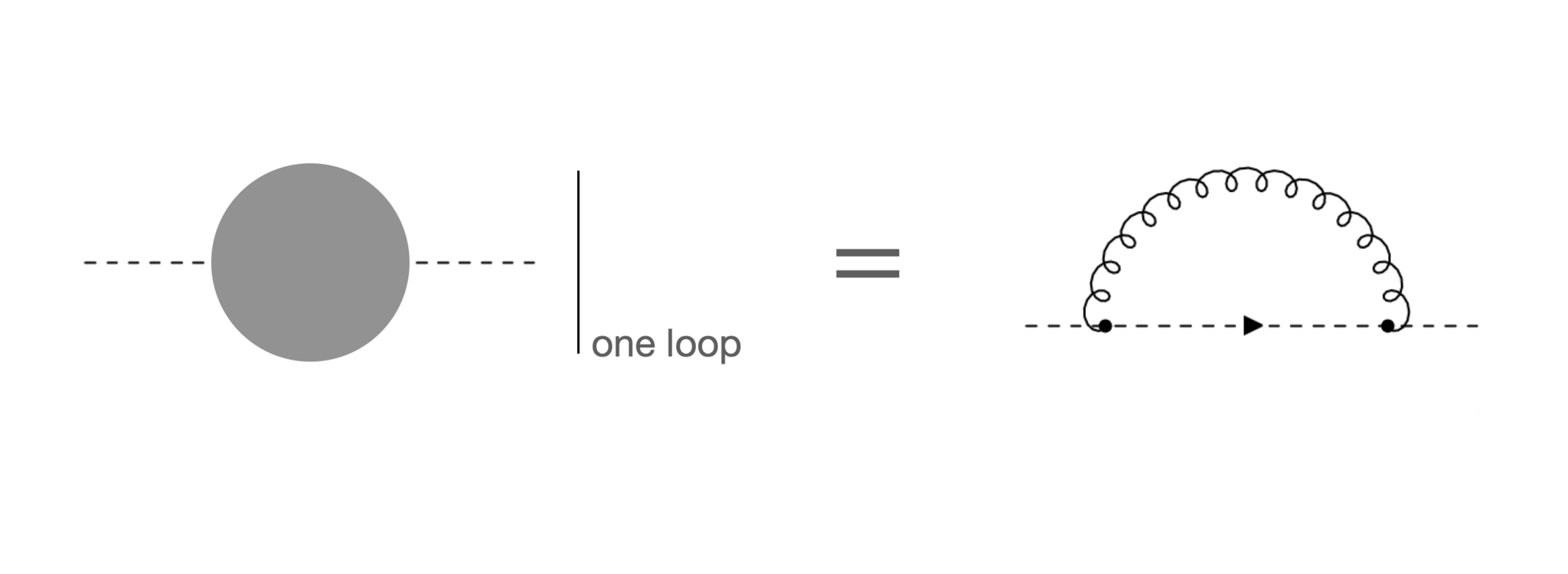
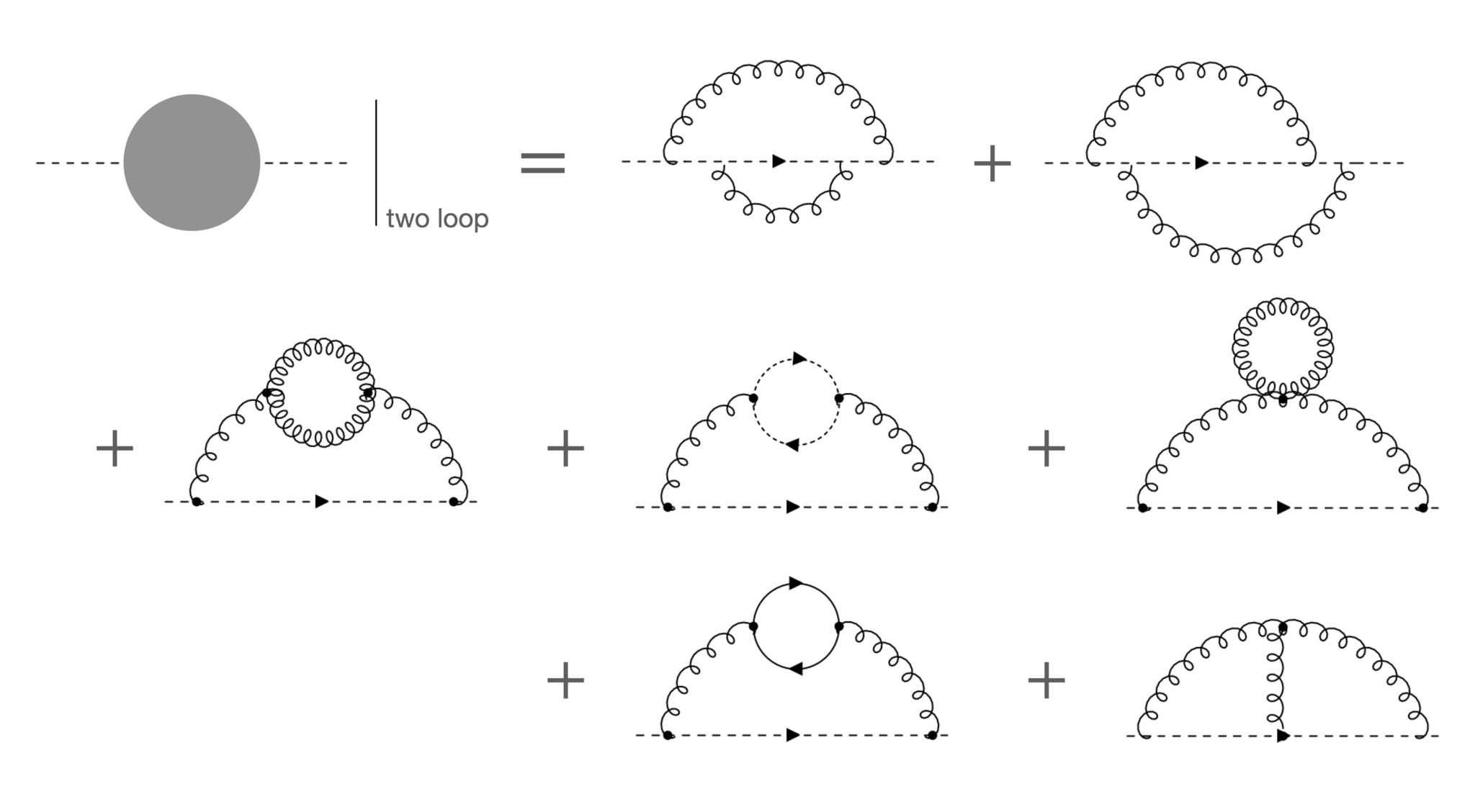$$g^2 \ \& \ g^4$（それぞれ上図と下図）の2点1PI頂点関数$ $g^2 \ & \ g^4$（それぞれ上図と下図）の2点1PI頂点関数
$g$ の次数は偶数のみです。
ファインマン則2
計算したい摂動の次数における $n$ 点関数に対応するダイアグラムを描き、以下のように式に変換します：
・「ファインマン則1」に従い、各パーツに付随した式をかけます
・vertexには運動量保存則が課されます。すなわち、あるvertexに入り込む運動量が $k_{1}^{μ}, k_{2}^{μ}, \dots,, k_{n}^{μ}$ ならば $\sum k_{i}^{μ} = 0$ が各 $μ$ ごとに課されます。
・ダイアグラムにループをなす部分がある場合、外線の運動量と運動量保存則では定まらない運動量が存在します。これに関しては積分を行います（違う運動量状態の量子力学的重ね合わせに対応する）。ループと積分の対応は以下です：

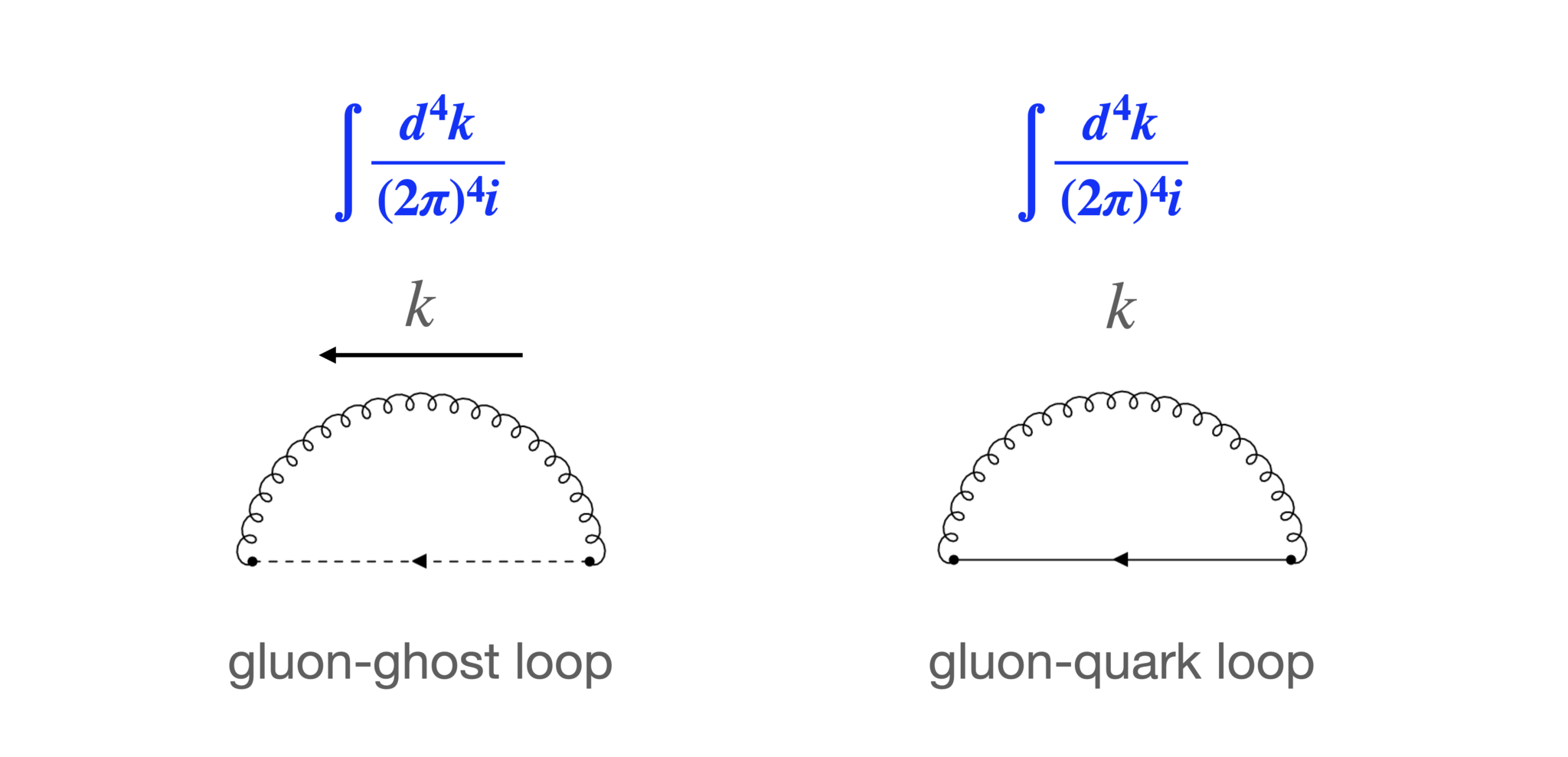各種ループにおける積分のファクター
・対称因子と呼ばれる数をかけます
積分はこのままではill-definedです。そこで積分に以下3つの操作を施します。
・propagatorのpoleを実軸から微小にずらす
・MinkowskiからEuclidに移る：複素平面上での被積分関数の解析性を用い、運動量積分のゼロ成分（＝エネルギー）を $k^{0} \to i k^{0}$ にする
・次元を4次元から $D = 4 - 2 ϵ$ （ $ϵ$ は微小な複素数）にずらす
これらの具体的な操作に関しては次の記事で説明します。
ダイアグラムに対応する式を計算し、これを $ϵ$ でLaurent展開します。すると一般に
$\frac{A}{ϵ} + (finite part) + O (ϵ)$
と書けます。 $A$ や $finite part$ は外線の運動量や $g_{μ ν}$ からなるtensorです。4次元では $ϵ \to 0$ だから、 $1 / ϵ$ の項は発散します。
発散を消すようにくりこみ定数を決めます。そのため、計算したダイアグラムの構造と同じcounter termを足します。counter term (CT)は以下のダイアグラムです。

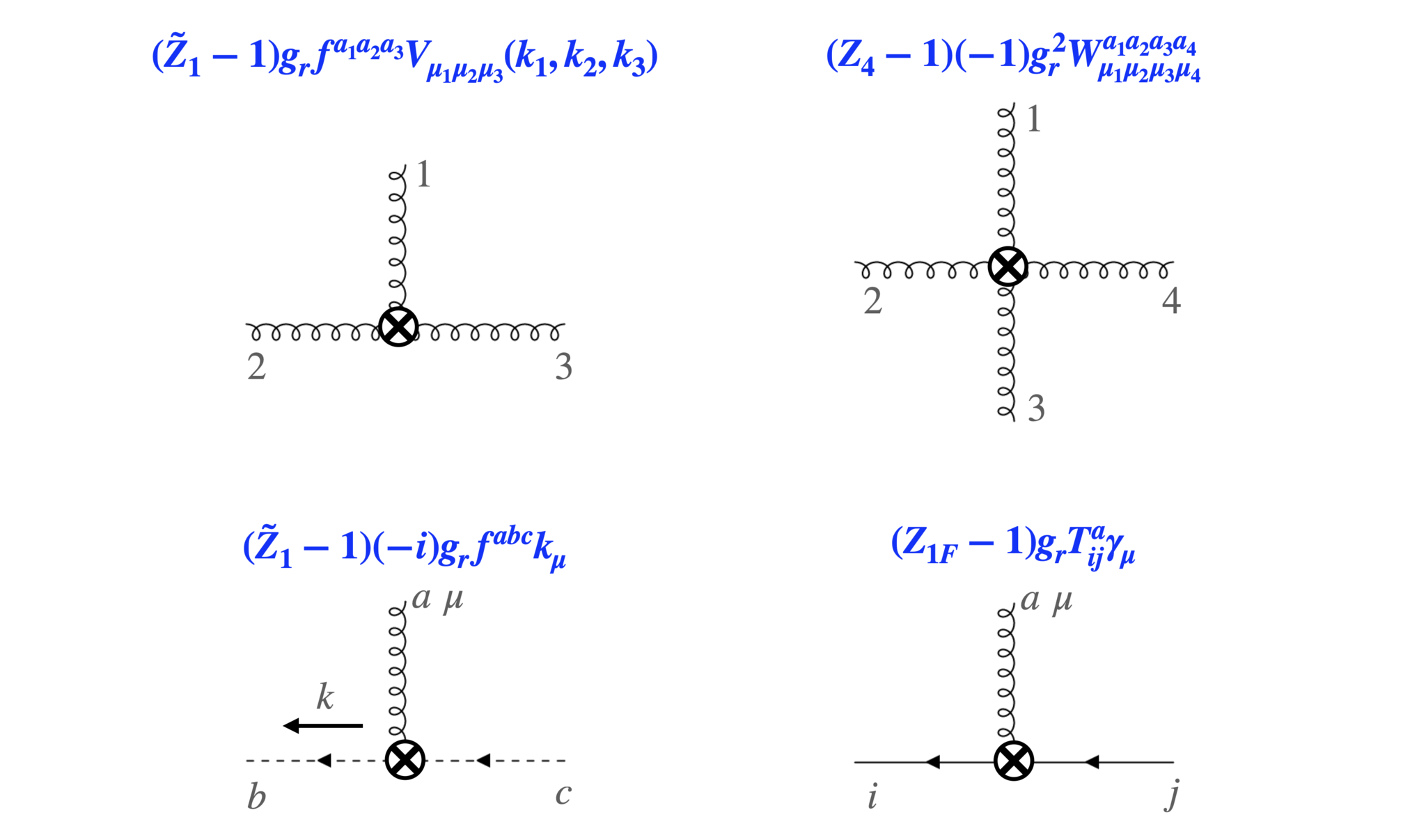各種counter term
$g_{r}$ はくりこまれた結合定数、 $m_{r}$ はくりこまれたquark質量であり、これらは有限の量です。 $Z_{i}$ や ${\tilde{Z}}_{i}$ はくりこみ定数です。そしてくりこみ定数を、「ダイアグラム+対応するCT」の、 $1 / ϵ$ に比例する発散部分が消えるように決めます（Minimal Subtraction(MS) schemeと呼ばれます）。
たとえば摂動の最低次でghostのpropagatorの発散を取り除くなら、図7のように、 ${\tilde{Z}}_{3}$ を用いて、左のループダイアグラムの発散項、すなわち $1 / ϵ$ に比例する部分を打ち消すように決定します。

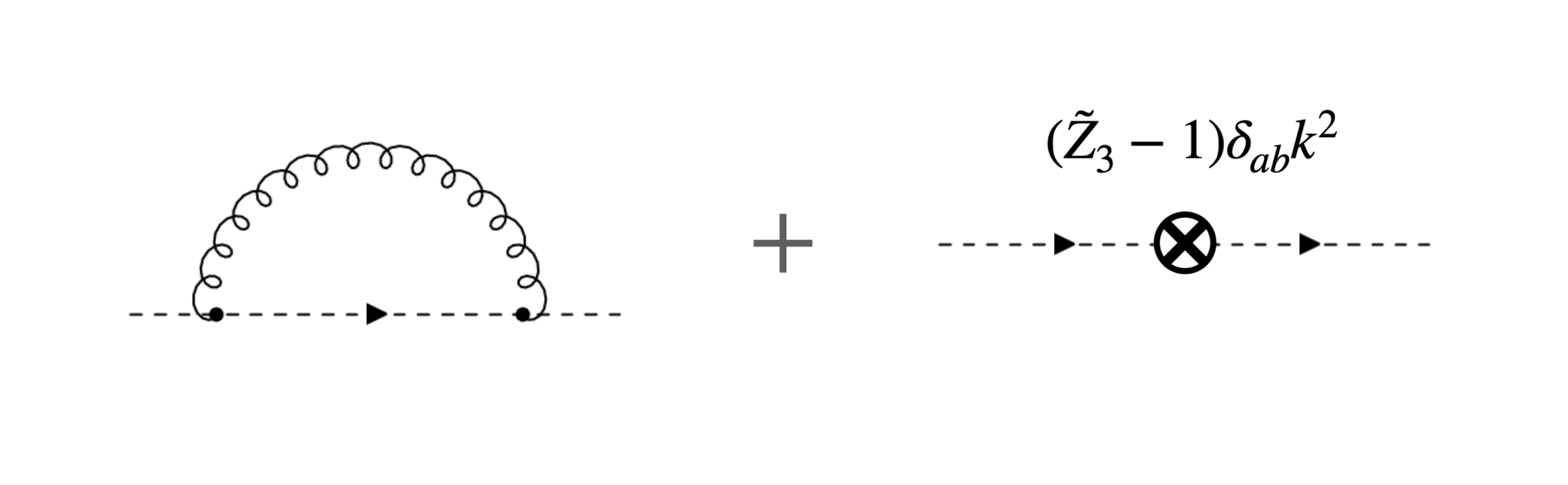ghostの2点1PI頂点関数のくりこみ

これでくりこみ定数を決定することができました。

ひとつ注意です。一連の記事では、摂動の $g^{2}$ のオーダーまでしか計算しません。この限りにおいて、CTは上記のものを用い、計算したダイアグラムと同じ種類のCTを足し、 $Z$ を決定すればよいです。一方 $g^{2}$ より高次の寄与を計算するときは、くりこみ定数も摂動展開し、各次数で発散を打ち消すようにこれを決定します。高次のダイアグラムは一般に、サブダイアグラムとして、低次の発散グラフを含みます。これらのサブダイアグラムの発散は、低次のくりこみ定数によるCTで消します。残ったダイアグラム全体の発散を、高次のくりこみ定数を使うことで消します。高次のくりこみに関しては、一連の記事では取り扱いません。

(B) 走る結合定数の計算

つぎに走る結合定数の計算の概要について述べます：

(B) 走る結合定数の計算

走る結合定数は、 $g = Z_{g} g_{r}$ の $Z_{g}$ の「典型的なエネルギー」への依存性から計算できます。

(A)の5.で、積分の次元を $4$ から $D = 4 - 2 ϵ$ にずらしました。そのため、裸の結合定数 $g$ は $μ$ を質量次元 $M^{0}$ をもつ量として、 $μ^{ϵ}$ と同じ次元を持ちます（次回記事で説明します）。 $g$ はもともとのLagrangianの結合定数なわけですが、(A)で述べたようにこれをくりこまれた結合定数 $g_{r}$ で $g = Z_{g} g_{r}$ と書き直し、 $Z_{g}$ に発散を吸収させ、ダイアグラムを有限化します。 $g$ は発散しており、 $g_{r}$ は有限です。

$Z_{g}$ は無次元だから、 $g_{r}$ も $g$ と同じ $μ^{ϵ}$ の次元を持ちます。ここで、無次元化した結合定数 $g_{R}$ を、
$g_{r} = g_{R} μ^{ϵ}$
として導入します。そして、裸の結合定数 $g$ は $μ$ に依存しないことを要請します。つまり
$μ \frac{d g}{d μ} = 0$
を課します。これはくりこみ群方程式です。
$g = Z_{g} g_{r} = Z_{g} (g_{R}) g_{R} μ^{ϵ}$ であり、 $g_{R}$ が $μ$ に依存するとして上式に代入すると
$\begin{array}{r} μ \frac{d}{d μ} Z_{g} (g_{R} (μ)) g_{R} (μ) μ^{ϵ} = 0 \leftrightarrow β = - ϵ g_{R} - \frac{μ}{Z_{g}} \frac{d Z_{g}}{d μ} g_{R} (β := μ \frac{d g_{R}}{μ}) \end{array}$
となります。この式にくりこみ操作で計算した $Z_{g}$ を代入すれば、 $β$ を $g_{R}$ の関数として書くことができます。これを解くことで $g_{R} (μ)$ が求まります。

$g_{R} (μ)$ はスケール $μ$ に依存する結合定数ですが、以降の記事で具体的に見るように、 $lim_{μ \to 0} g_{R} (μ) = 0$ を満たします。すなわち、YM理論は高エネルギーで相互作用が弱くなり、グルーオンやクォークは自由粒子に近い振る舞いをします。この性質は漸近的自由性と呼ばれ、QCD（SU(3)のYM理論）が強い相互作用の基礎理論である1つの強い根拠です。

計算の簡略化

一連の記事では次のような簡略化をします：

$Z_{g}$ のみ計算する
Eq.(2)の ${\tilde{Z}}_{1} = Z_{g} {\tilde{Z}}_{3} Z_{3}^{1 / 2}$ により $Z_{g}$ を計算する
MS schemeにおける $Z_{g}$ の決定には、発散項= $1 / ϵ$ に比例する部分だけが必要

以下それぞれの説明です。

1.に関して：走る結合定数を計算するには、結合定数のくりこみ定数 $Z_{g}$ のみが必要です。一連の記事では、 $Z_{g}$ のみ計算し、これに必要のないくりこみ定数は計算しません。
2.に関して： $Z_{g}$ はEq.(2)より、4つの求め方があります。一連の記事では、Ref.[1]に習い、
${\tilde{Z}}_{1} = Z_{g} {\tilde{Z}}_{3} Z_{3}^{1 / 2}$
を使って求めます。これはすなわち、ghost-gluon vertexのくりこみ定数 ${\tilde{Z}}_{1}$ 、ghost propagatorのくりこみ定数 ${\tilde{Z}}_{3}$ 、gluon propagatorのくりこみ定数 $Z_{3}$ から $Z_{g}$ を定めるということです。よってこれら3種類のダイアグラムの計算を行います。これは比較的簡単な $Z_{g}$ の計算法です。
3.に関して：すべてのダイアグラムを $ϵ^{0}$ のオーダーまで計算するのはちょっと大変です。しかしMS schemeでは、 $1 / ϵ$ の発散部分のみくりこみ定数で打ち消すので、発散部さえ計算すればこれを決定することができます。一連の記事において、基本的には $ϵ^{0}$ のオーダーまで計算を行いますが、gluon-ghost vertexに関しては発散部分のみ計算する予定です。