走る結合定数の計算(3/5): 摂動計算に関する数学公式集

はじめに
公式集
ゲージ群の生成子に関わる公式
$i ϵ$ 処方、Feynman prescription
次元正則化
被積分関数の分母をまとめる： Feynman parametrization
対称性から導かれる公式
虚時間方向への積分路の変更
$D$ 次元の極座標表示
分母がまとまっている場合のループ積分
$D$ 次元における物理量の次元解析
ループ積分の公式
ベータ関数 $B (x, y)$ の性質
$B$ 関数を $B (2 - ϵ, 2 - ϵ)$ に書き換える
有用な積分の公式
$Γ$ 関数、 $B$ 関数の極に関する公式
$D$ 次元のDirac行列に関する公式
まとめ
Appendix: 公式4の2.の証明
参考文献

大学数学基礎解説

文献あり

走る結合定数の計算(3/5): 摂動計算に関する数学公式集

場の量子論,くりこみ,ゲージ理論

271

★ 本記事は走る結合定数の計算(2/5):Yang-Mills理論のくりこみの続きです。前回の冒頭に示した表記の規約に従います。

【更新履歴】（左の▶をクリックで表示）

06Aug.2022: 公式4の1.の2つ目の式の積分範囲が間違っていたので修正しました。正しくは

\begin{array}{r} \frac{1}{A_{1} A_{2} A_{3}} = 2 \int_{0}^{1} d x \int_{0}^{1 - x} d y \frac{1}{(x A_{1} + y A_{2} + (1 - x - y) A_{3})^{3}} \end{array}

です

11Aug.2022: 公式の順番を入れ替え、実際の計算手順に沿うようにしました。 ループ計算は

i ϵ

処方

\to

次元正則化

\to

Feynman parametrization

\to

積分する変数のうちindexが浮いているものを対称性を用いて消す & 縮約する

\to

Wick rotation & 極座標への変換

\to

積分する

という手順で行うのが一般的かと思いますので、この順番に並べ替えました。説明も変更しています。公式番号も変更しましたのでご注意ください

はじめに

Yang-Mills(YM)理論の走る結合定数を計算する記事の第3回です。

前回はYM理論におけるくりこみ定数の決定、および走る結合定数の計算に関して説明しました。今回はダイアグラムの計算・くりこみに使う公式をまとめます。ここでは主に次元正則化において用いる公式を示します。Ref.[1]およびRef.[2]を参考にした部分が多いです。証明は概略のみ示しています。

具体的なダイアグラムの計算は次回行います。

公式集

ゲージ群の生成子に関わる公式

ダイアグラムの評価には、ゲージ群のインデックスに関わる群論的ファクターが現れます。これに関する公式をまとめます。

ゲージ群の生成子・構造定数に関連する公式

構造定数 $f_{a b c}$ は、ゲージ群の生成子 $T^{a}$ を用いて
$\begin{array}{r} [T^{a}, T^{b}] = i f_{a b c} T^{c} \end{array}$
で定義される。 $f_{a b c}$ は添字の入れ替えに関し完全反対称。
$T_{b c}^{a} := - i f_{a b c}$ はSU(N)の生成子である。すなわちこの $T$ に対して
$\begin{array}{r} [T^{a}, T^{b}] = i f_{a b c} T^{c} \end{array}$
が成立する。この表現をadjoint表現と呼ぶ。
ゲージ群の生成子に関する公式：
$\begin{aligned} t r (T^{a} T^{b}) & = \frac{δ_{a b}}{2}, \\ T_{i j}^{a} T_{k l}^{a} & = \frac{1}{2} (δ_{i l} δ_{j k} - \frac{1}{N} δ_{i j} δ_{k l}), \\ (T^{a} T^{b})_{i j} & = C_{F} δ_{i j}, C_{F} = \frac{N^{2} - 1}{2 N} \end{aligned}$
構造定数に関する公式：
$\begin{aligned} f^{a c d} f^{b c d} & = δ_{a b} N, \\ f^{a d e} f^{b e f} f^{c f d} & = \frac{N}{2} f^{a b c} \end{aligned}$
生成子に対するJacobi恒等式から導かれる等式：
$\begin{array}{r} f_{b c d} f_{a d e} + f_{c a d} f_{b d e} + f_{a b d} f_{c d e} = 0 \end{array}$

1.は定義。2.は計算すれば確かめられる。3.の1つ目の式は定義。
3.の上から2番目の式は、生成子の線形独立性から示せる。任意の行列は $M = M_{0} 1 + M_{a} T^{a}$ と書け、 $t r T^{a} = 0, t r (T^{a} T^{b}) = δ_{a b} / 2$ より $M_{0} = t r M / 2, M_{a} = 2 t r (M T^{a})$ である。これを $M = M_{0} 1 + M_{a} T^{a}$ に入れて書き換えると $δ_{i l} δ_{j k} M_{l k} = (\frac{1}{N} δ_{i j} δ_{k l} + 2 T_{i j} T_{k l}) M_{l k}$ が示せるので求める式が得られる。
この式と $f^{a b c}$ が生成子の表現であることから、3.4.の式が証明できる。
5.はJacobi恒等式: $[[T^{a}, T^{b}], T^{c}] + [[T^{c}, T^{a}], T^{b}] + [[T^{b}, T^{c}], T^{a}] = 0$ から従う。

$i ϵ$ 処方、Feynman prescription

ループ積分の被積分関数のpoleを実軸からずらし、積分をwell-definedにします。以下の処方が典型的です。

i ϵ

処方

以下のように、propagatorのpoleを実軸から微小にずらす（ $ϵ$ は微小な複素数）:
$\frac{1}{q^{2} - m^{2}} \to \frac{1}{q^{2} - m^{2} + i ϵ}$
このようにずらしたpropagatorのフーリエ変換は以下のようになる:
$\begin{aligned} D_{F} (x - y) & := \int \frac{d^{4} q}{(2 π)^{4}} \frac{i}{q^{2} - m^{2} + i ϵ} e^{- i q \cdot (x - y)} \\ = {\begin{cases} D (x - y) & for x^{0} > y^{0} \\ D (y - x) & for x^{0} < y^{0} \end{cases} \\ (2-1) & = θ (x^{0} - y^{0}) ⟨ 0 | \hat{ϕ} (x) \hat{ϕ} (y) | 0 ⟩ + θ (y^{0} - x^{0}) ⟨ 0 | \hat{ϕ} (y) \hat{ϕ} (x) | 0 ⟩ \end{aligned}$
ここで
$\begin{array}{r} (2-2) & D (x - y) := {\int \frac{d^{3} q}{(2 π)^{3}} \frac{1}{2 E_{q}} e^{- i q \cdot (x - y)} |}_{q^{0} = E_{q}} = ⟨ 0 | \hat{ϕ} (x) \hat{ϕ} (y) | 0 ⟩, E_{q} := \sqrt{{\vec{q}}^{2} + m^{2}} \end{array}$
である。
演算子 $T$ を
$\begin{array}{r} T \hat{ϕ} (x) \hat{ϕ} (y) = {\begin{cases} \hat{ϕ} (x) \hat{ϕ} (y) & x_{0} > y_{0} \\ \hat{ϕ} (y) \hat{ϕ} (x) & y_{0} > x_{0} \end{cases} \end{array}$
（このような積をtime ordered productと呼ぶ）
で定義すれば
$\begin{array}{r} D_{F} (x - y) = ⟨ 0 | T \hat{ϕ} (x) \hat{ϕ} (y) | 0 ⟩ \end{array}$
となる。 $D_{F} (x - y)$ はFeynman propagatorと呼ばれる。

Feynman propagatorの!FORMULA[32][36705958][0]積分のcontour Feynman propagatorの $q_{0}$ 積分のcontour

$\hat{ϕ} (x)$ は正準量子化で量子化された場の演算子であるが、説明を省略する。
ここでは $D_{F} (x - y)$ が $D (x - y) (x^{0} > y^{0})$ および $D (y - x) (x^{0} < y^{0})$ となることを示す。
$D_{F} (x - y)$ の定義において、 $q_{0}$ 積分を実行する。そのために、 $q_{0}$ を複素平面に拡張し、留数定理を用いる（図1）。 $q^{0}$ 平面上の積分経路として、実軸 $C_{1} : - \infty \to \infty$ と、極座標における上下半円の経路 $C_{2}^{\pm} : (r = + \infty, θ = 0 \to \pm π)$ を考える。 $x_{0} - y_{0} > 0$ なら、 $e^{- i p \cdot (x - y)}$ のファクターにより $C_{2}^{-}$ の寄与は０なので $C_{1} + C_{2}^{-}$ （青の経路）を、逆なら $C_{1} + C_{2}^{+}$ （オレンジの経路）を採用する。すると、 $x_{0} - y_{0}$ の正負の違いにより、積分に効く $1 / (q^{2} - m^{2} + i ϵ) = 1 / (q^{0} + E_{q} - i ϵ) / (q^{0} - E_{q} + i ϵ)$ のpoleが異なる。これを考慮して計算すれば、Eq(2-2)よりEq.(2-1)を得る。 $_{◼}$

このような処方を"Feynman prescription"とか" $i ϵ$ 処方"と呼びます。
場の理論の摂動論はFeynman propagatorを使って構成します。

次元正則化

次元を $4$ からずらします。YM理論の場合、この操作でループ積分は有限になります。

次元正則化

$\begin{array}{r} 4 dim. \to D := 4 - 2 ϵ \end{array}$
ここで $ϵ$ は一般に複素数であり、微小なパラメータとして取り扱う。 $ϵ \to 0$ が $D = 4$ の極限。これによりループ積分は
$\int \frac{d^{4} q}{(2 π)^{4} i} \to \int \frac{d^{D} q}{(2 π)^{D} i}$
となる。

このような操作は一般に正則化と呼ばれます。次元正則化は理論の様々な対称性を保つため有用です。YMの場合この正則化でゲージ対称性が保たれることが重要です。

正則化をしたのち、ダイアグラムを計算し $ϵ$ でLaurent展開して、 $ϵ$ の負ベキの発散部分をくりこみで除去します。

被積分関数の分母をまとめる： Feynman parametrization

ループ積分を実行するため、被積分関数の分母をまとめます。ループ積分には、例えば以下のようなものがあります：
$\begin{array}{r} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{q^{2} + i ϵ} \frac{1}{(q - p)^{2} + i ϵ} \end{array}$
これは2つの分数関数の積ですが、これを1つにまとめます。

Feynman parametrization

被積分関数の分母をまとめる：
$\begin{aligned} \frac{1}{A_{1} A_{2}} & = \int_{0}^{1} \frac{d x}{(x A_{1} + (1 - x) A_{2})^{2}}, \\ \frac{1}{A_{1} A_{2} A_{3}} & = 2 \int_{0}^{1} d x \int_{0}^{1 - x} d y \frac{1}{(x A_{1} + y A_{2} + (1 - x - y) A_{3})^{3}} \end{aligned}$
下は
$\begin{aligned} \frac{1}{A_{1} A_{2} A_{3}} & = 2 \int_{0}^{1} d x \int_{0}^{1} d y \frac{y}{((A_{1} - A_{2}) x y + (A_{2} - A_{3}) y + A_{3})^{3}} \end{aligned}$
とも書ける。積分範囲の違いに注意。
$1 / (A^{α} B^{β})$ の分母をまとめる：
$\frac{1}{A^{α} B^{β}} = \frac{Γ (α + β)}{Γ (α) Γ (β)} \int_{0}^{1} d x d y \frac{x^{α - 1} y^{β - 1}}{(x A + y B)^{α + β}} δ (1 - x - y)$
一般に以下が成立する：
$\frac{1}{A_{1} \dots A_{N}} = Γ [N] \int_{0}^{1} d x_{1} \dots d x_{N} δ (1 - \sum_{j = 1}^{N} x_{j}) \frac{1}{[A_{1} x_{1} + \dots + A_{N} x_{N}]^{N}}$
これはまた以下のようにも書ける：
$\frac{1}{A_{1} \dots A_{N}} = Γ [N] \int_{0}^{1} d x_{1} \dots d x_{N - 1} \frac{x_{2} x_{3}^{2} \dots x_{N - 1}^{N - 2}}{[(A_{1} - A_{2}) x_{1} \dots x_{N - 1} + (A_{2} - A_{3}) x_{2} \dots x_{N - 1} + \dots + (A_{N - 1} - A_{N}) x_{N - 1} + A_{N}]^{N}}$

1.はふつうに積分すれば証明できる。
2.は、まず、公式9の1.（後述）から右辺の積分の係数は $(B (α, β))^{- 1}$ であることに注意する。右辺で $y$ を積分すれば
$\begin{aligned} (B (α, β))^{- 1} \int_{0}^{1} d x d y \frac{x^{α - 1} y^{β - 1}}{(x A + y B)^{α + β}} δ (1 - x - y) & = \frac{1}{A^{α} B^{β}} \times (B (α, β))^{- 1} \times γ^{β} \int_{0}^{1} d x \frac{x^{α - 1} (1 - x)^{β - 1}}{{x + γ (1 - x)}^{α + β}} \\ (γ := B / A) \end{aligned}$
となるが、 $x = 1 / (1 + t / γ)$ と変数変換すれば
$= \frac{1}{A^{α} B^{β}} \times (B (α, β))^{- 1} \int_{0}^{\infty} d t \frac{t^{β - 1}}{(1 + t)^{α + β}}$
を得る。この積分は公式9の1.より $B (α, β)$ なので、与えられた式を得る。
3.の上の関係式はAppendixで証明する。下の関係式は公式4の2.を使えば帰納法で証明できる。または上の関係式に変数変換を施しても導ける。

上に示した例
$\begin{array}{r} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{q^{2} + i ϵ} \frac{1}{(q - p)^{2} + i ϵ} \end{array}$
の場合、この作業で
$\begin{aligned} \int_{0}^{1} d x \int \frac{d^{D} \tilde{q}}{(2 π)^{D} i} \frac{1}{({\tilde{q}}^{2} - Δ + i ϵ)^{2}} \\ \tilde{q} := q - k (1 - x), Δ := - k^{2} x (1 - x) \end{aligned}$
になります。 $\tilde{q}$ への変数変換ののち、分母は ${\tilde{q}}^{2}$ の関数になることは重要です。

対称性から導かれる公式

ループ積分において、対称性を用いることで、積分変数のLorentzの足を縮約できる場合があります。

以下が成立する：

$\int d^{D} q q_{μ} f (q^{2}) = 0$
$\int d^{D} q q_{μ} q_{ν} f (q^{2}) = \frac{1}{D} g_{μ ν} \int d^{D} q q^{2} f (q^{2})$
$\int d^{D} q q_{μ} q_{ν} q_{ρ} f (q^{2}) = 0$
$\int d^{D} q q_{μ} q_{ν} q_{ρ} q_{σ} f (q^{2}) = \frac{1}{D (D + 2)} g_{(μ ν} g_{ρ σ)} \int d^{D} q (q^{2})^{2} f (q^{2}) g_{(μ ν} g_{ρ σ)} := g_{μ ν} g_{ρ σ} + g_{μ ρ} g_{ν σ} + g_{μ σ} g_{ν ρ}$

1.と3.は積分後 $μ$ の足をもつLorentz vectorが存在しないことから明らか（時空の回転対称性を破る量がない）。
2.は積分後 $μ, ν$ の足をもつtensorは $g_{μ ν}$ しかありえない。よって
$\begin{array}{r} (5-1) & \int d^{D} q q_{μ} q_{ν} f (q^{2}) = L g_{μ ν} \end{array}$
となる。両辺に $g^{μ ν}$ をかけると、 $g^{μ ν} g_{μ ν} = D$ より
$\begin{array}{r} \int d^{D} q^{2} f (q^{2}) = D L \\ ∴ L = \frac{1}{D} \int d^{D} q^{2} f (q^{2}) \end{array}$
を得る。
3.は2.と同様。この積分は対称性より $g_{(μ ν} g_{ρ σ)}$ に比例することを用い、2.と同様の計算をすればよい。

被積分関数の $f$ は $f (q^{2})$ であり、引数の $q_{μ}$ のindexが自身と縮約されていることに注意してください。 $q$ と外線の運動量のindexが縮約されている項が存在する場合（=時空回転の基準が存在する場合）、上の式は成立しません。

以下は（次元正則化や対称性などより）ゼロになります：

ゼロとなる積分

$\int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{(- q^{2})^{α}} = 0 (α > 0)$ （次元正則化で成立する式）
$\int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{(q^{2})^{α}} = 0$ （ $∵$ 回転対称性による）
$\int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{(q^{2})^{α}} = 0 (α > 1)$ （ $∵$ 積分は $g_{μ ν}$ に比例するしかないが、そうすると1.から0になる）

1.は次元正則化において、ある操作を施すことで正当化される。自明に成立することではないので、定義のようなものだと思えば良い。詳しくは例えばRef.[1]P172参照。

Feynman parametrizationののち、被積分関数の分母は ${\tilde{q}}^{2}$ の関数になります。すると、分子に $\tilde{q}$ の関数があり、かつそのLorentzのindexが浮いている場合（または外線の運動量と縮約をとっている場合）、公式5を用いることで、その項を消す、またはindexを縮約することができます。これはこの後のWick rotationにおいて重要です。

虚時間方向への積分路の変更

次に、 $q^{0}$ を虚軸にもっていくことで、Euclid計量での積分に直します $^{(*)}$ 。これにより極座標に移り、積分を実行します。

Euclid化、Wick rotation

以下の変数変換: $q \to q_{E}$ （Euclid化やWick rotationと呼ぶ）を行い、積分を極座標にする:
$\begin{aligned} q_{0} & = i {q_{E}}_{0} ({q_{E}}_{0} : real), \vec{q} = {\vec{q}}_{E} \\ d^{D} q & = i d^{D} q_{E}, q^{2} = - q_{E}^{2}, q_{E}^{2} = {q_{E}}_{0}^{2} + {\vec{q}}_{E}^{2} \\ d^{D} q_{E} & = q_{E}^{D - 1} d q_{E} d Ω_{D} \end{aligned}$
$d Ω_{D}$ は $D$ 次元における極座標の角度方向の積分測度。
この操作は、被積分関数のpoleが第1・第3象限になければ正当化される。

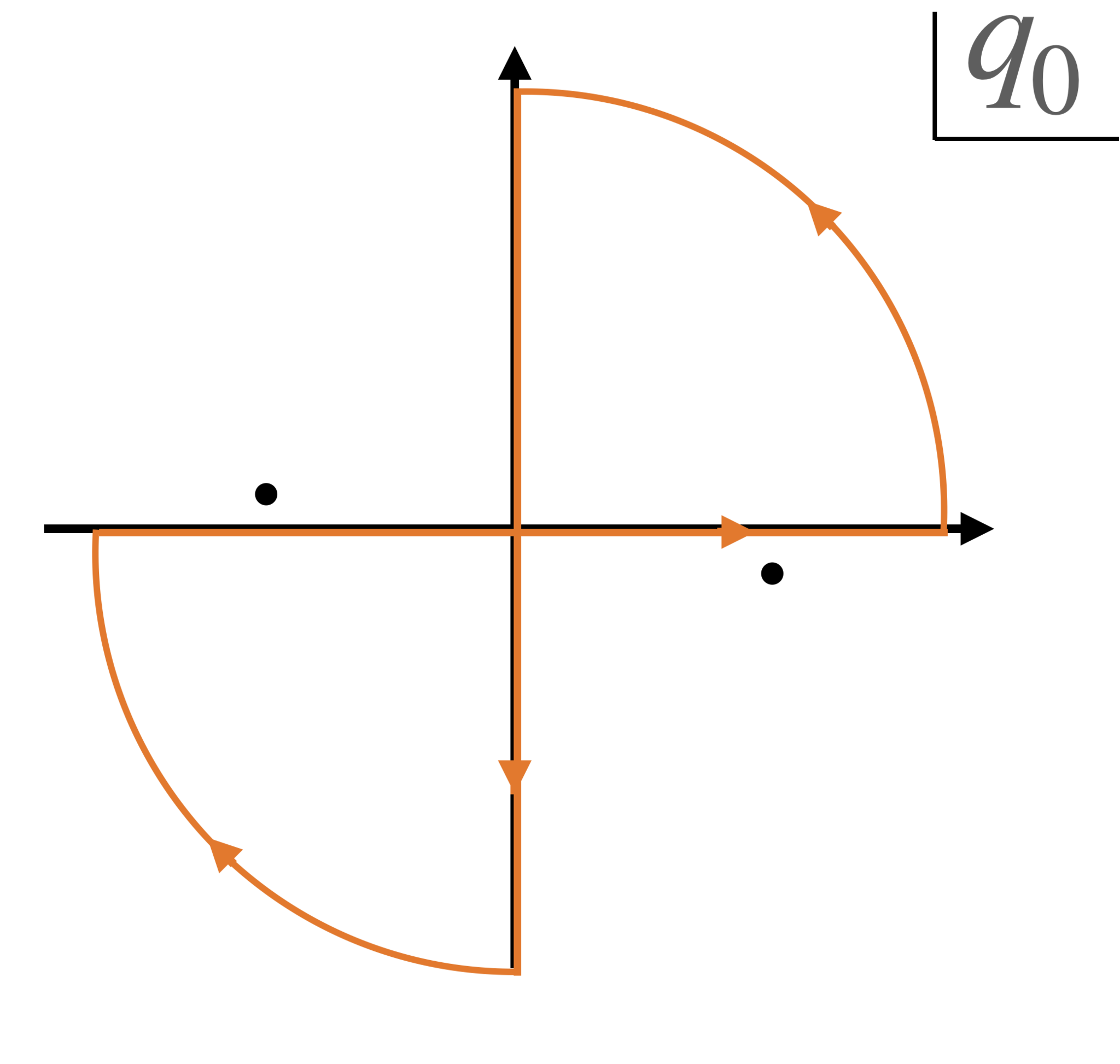Wick rotation

被積分関数を $(- q^{2})^{b} / (Δ - q^{2} - i ϵ)^{a}$ とする。ここまで説明した操作を施した後、被積分関数はこの類の関数に帰着する。
複素 $q^{0}$ 平面において、積分路を虚軸から実軸に移すため、図1の積分路で積分する。積分路内部にはpoleが存在しないこと、また無限遠の1/4円部分が消えることを用いれば
$\begin{array}{r} \int_{- \infty}^{\infty} \frac{d q^{0}}{(2 π) i} \int \frac{d^{D - 1} q}{(2 π)^{D - 1}} \frac{(- q^{2})^{b}}{(Δ^{2} - q^{2} - i ϵ)^{a}} = - \int_{+ i \infty}^{- i \infty} \frac{d q^{0}}{(2 π) i} \int \frac{d^{D - 1} q}{(2 π)^{D - 1}} \frac{(- q^{2})^{b}}{(Δ^{2} - q^{2} - i ϵ)^{a}} \end{array}$
を得る。 $q_{E}^{0} := - i q^{0}, q_{E}^{i} := q^{i}, q_{E}^{2} = (q_{E}^{0})^{2} + {\vec{q}}_{E}^{2}$ とすれば
$\begin{aligned} = - \int_{\infty}^{- \infty} \frac{d q_{E}^{0}}{(2 π)} \int \frac{d^{D - 1} q_{E}}{(2 π)^{D - 1}} \frac{({q_{E}^{0}}^{2} + {\vec{q}}_{E}^{2})^{b}}{(Δ^{2} + {q_{E}^{0}}^{2} + {\vec{q}}_{E}^{2} - i ϵ)^{a}} \\ = \int_{- \infty}^{\infty} \frac{d q_{E}^{0}}{(2 π)} \int \frac{d^{D - 1} q_{E}}{(2 π)^{D - 1}} \frac{(q_{E})^{b}}{(Δ + q_{E}^{2} - i ϵ)^{a}} \\ = \int \frac{d^{D} q_{E}}{(2 π)^{D}} \frac{(q_{E})^{b}}{(Δ + q_{E}^{2} - i ϵ)^{a}} \end{aligned}$
あとは積分を極座標にすれば、公式7のWick rotationの操作と一致する。

$D$ 次元の極座標表示

$D$ 次元の極座標への座標変換およびJacobianは以下のようになります：

$x \in R^{D}$ のとき,極座標への変数変換は以下:
$\begin{array}{r} {\begin{cases} x_{1} & = r \cos θ, \\ x_{2} & = r \sin θ \cos φ_{1}, \\ x_{3} & = r \sin θ \sin φ_{1} \cos φ_{2}, \\ ⋮ \\ x_{D - 1} & = r \sin θ \sin φ_{1} \dots \sin φ_{D - 3} \sin φ_{D - 2}, \\ x_{D} & = r \sin θ \sin φ_{1} \dots \sin φ_{D - 3} \cos φ_{D - 2} \end{cases} \end{array}$
各変数の変化域は以下:
$\begin{array}{r} 0 \leq r \leq + \infty, 0 \leq θ, φ_{1}, \dots, φ_{D - 3} \leq π, 0 \leq φ_{D - 2} \leq 2 π \end{array}$
Jacobianは以下のように書ける:
$\begin{array}{r} r^{D - 1} \sin^{D - 2} θ \sin^{D - 3} φ_{1} \dots \sin φ_{D - 3} . \end{array}$
よって
$\begin{array}{r} \prod_{i} d x_{i} = r^{D - 1} \sin^{D - 2} θ \sin^{D - 3} φ_{1} \dots \sin φ_{D - 3} d r d θ d φ_{1} \dots d φ_{D - 2} \end{array}$
ゆえに $d Ω_{D}$ は
$\begin{array}{r} d Ω_{D} = \sin^{D - 2} θ \sin^{D - 3} φ_{1} \dots \sin φ_{D - 3} d θ d φ_{1} \dots d φ_{D - 3} d φ_{D - 2} \end{array}$
$d Ω_{D}$ の角度積分(= $D$ 次元の半径1の超球の表面積):
$\begin{aligned} \int d Ω_{D} & = \int_{0}^{π} d θ \int_{0}^{π} d φ_{1} \dots \int_{0}^{π} d φ_{D - 3} \int_{0}^{2 π} d φ_{D - 2} \sin^{D - 2} θ \sin^{D - 3} φ_{1} \dots \sin φ_{D - 3} d θ d φ_{1} \dots d φ_{D - 3} d φ_{D - 2} \\ = \frac{2 π^{D / 2}}{Γ (D / 2)} \end{aligned}$

$d Ω_{D}$ が上で示した形になるのは、例えば帰納法で証明できる（参考：倭算数理研究所）。 $D = k$ のとき上記の $d Ω_{D}$ の成立を仮定し、直交座標 $\to$ 円柱座標 $\to$ 極座標という2段階の変数変換を施すことで、 $D = k + 1$ でも正しいことが示せる。
$\int d Ω_{D}$ の計算は以下のようにする。
ガウス積分より $(\int_{- \infty}^{\infty} e^{- x^{2}} d x)^{D} = π^{D / 2}$ であるが、これを極座標で表せば $\int_{0}^{\infty} d r r^{D - 1} e^{- r^{2}} \times \int d Ω_{D}$ 。ガンマ関数の定義より $\int_{0}^{\infty} d r r^{D - 1} e^{- r^{2}} = Γ (D / 2) / 2$ であるから、 $\int d Ω_{D} = 2 π^{D / 2} / Γ (D / 2)$ を得る。

分母がまとまっている場合のループ積分

ループ積分の中心的な公式が公式9の2.,3.,4.です。

$B$ 関数の性質：
$\begin{aligned} B (p, q) & := \int_{0}^{1} d x x^{p - 1} (1 - x)^{q - 1} \\ = \int_{0}^{\infty} \frac{t^{p - 1}}{(1 + t)^{p + q}} d t = \frac{Γ (p) Γ (q)}{Γ (p + q)} \end{aligned}$
$\int \frac{d^{D} q_{E}}{(2 π)^{D}} \frac{1}{(q_{E}^{2} + Δ)^{a}} = \frac{Γ (a - D / 2)}{(4 π)^{D / 2} Γ (a)} Δ^{D / 2 - a}$
$\int \frac{d^{D} q_{E}}{(2 π)^{D}} \frac{q_{E}^{2}}{(q_{E}^{2} + Δ)^{a}} = \frac{D}{2} \frac{Γ (a - D / 2 - 1)}{(4 π)^{D / 2} Γ (a)} Δ^{D / 2 - a + 1}$
$\int \frac{d^{D} q_{E}}{(2 π)^{D}} \frac{(q_{E}^{2})^{2}}{(q_{E}^{2} + Δ)^{a}} = \frac{1}{4} D (D + 2) \frac{Γ (a - D / 2 - 2)}{(4 π)^{D / 2} Γ (a)} Δ^{D / 2 - a + 2}$

1.の $B (p, q) := \dots$ の2行目の1つ目の等式は $t = 1 / (1 - x) - 1$ と変数変換すれば直ちに得られる。
2つ目の等式は $Γ$ 関数の積分表示を用いて $Γ (p) Γ (q) = \int \int s^{x - 1} t^{y - 1} e^{- s} e^{- t} d t d s$ と書いておき、変数変換 $s = u v, t = u (1 - v)$ を施すと、 $Γ (p) γ (q) = Γ (p + q) B (p, q)$ を得る。
2.は極座標へ変換したのち、 $\int d Ω_{D} = \frac{2 π^{D / 2}}{Γ (D / 2)}$ と1.より導ける。
3.,4.は2.と同様。

$D$ 次元における物理量の次元解析

$D$ 次元では、4次元では質量次元0だった $g$ が次元を持ちます。

g

の次元

次元正則化において、YM理論の $g$ は質量次元 $ϵ$ をもつ： $[g] = M^{ϵ}$
（ $[A]$ は $A$ の質量次元を表す。 $A$ の質量次元が $α$ であることを $[A] = M^{α}$ で表す）

計算する際の前提は以下：

$x^{μ}$ の質量次元は $M^{- 1}$ 、粒子の質量 $m$ の質量次元は $M^{1}$
作用 $S$ は $ℏ$ と同じ次元をもつ。自然単位系では $[ℏ] = M^{0}$ なので、 $[S] = M^{0}$

これらより結合定数 $g$ の質量次元が計算できる。
まずゲージ場の運動項より
$\int d^{D} x \partial_{μ} A_{ν} \partial^{μ} A^{ν}$
は次元なし。よって
$[\partial_{μ} A_{ν} \partial^{μ} A^{ν}] = M^{D} ∴ [A] = M^{(D - 2) / 2}$
つぎにgluonの4点相互作用
$g^{2} A^{4}$
の項を考えると
$[g^{2} A^{4}] = M^{D} ∴ [g] = M^{(D - 2 (D - 2)) / 2} = M^{(4 - D) / 2}$
$D = 4 - 2 ϵ$ とすると
$[g] = M^{ϵ}$
となる。

ループ積分の公式

ここまで説明した手法・公式を使うと、以下のループ積分に関する公式が示せます（積分はWick rotationする前の表式です）:

ループ積分の公式1

分子が1:
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{(- q^{2})^{α} (- (q + k)^{2})^{β}} \\ = (4 π)^{- D / 2} (- k^{2})^{D / 2 - α - β} \frac{Γ (α + β - D / 2)}{Γ (α) Γ (β)} B (\frac{D}{2} - α, \frac{D}{2} - β) \\ = (4 π)^{- (2 - ϵ)} (- k^{2})^{(2 - ϵ) - α - β} \frac{Γ (α + β - (2 - ϵ))}{Γ (α) Γ (β)} B ((2 - ϵ) - α, (2 - ϵ) - β) \end{aligned}$
分子が $q_{μ}$ :
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{(- q^{2})^{α} (- (q + k)^{2})^{β}} \\ = - (4 π)^{- D / 2} k_{μ} (- k^{2})^{D / 2 - α - β} \frac{Γ (α + β - D / 2)}{Γ (α) Γ (β)} B (\frac{D}{2} - α + 1, \frac{D}{2} - β) \\ = - (4 π)^{- (2 - ϵ)} k_{μ} (- k^{2})^{(2 - ϵ) - α - β} \frac{Γ (α + β - (2 - ϵ))}{Γ (α) Γ (β)} B ((2 - ϵ) - α + 1, (2 - ϵ) - β) \end{aligned}$
分子が $q_{μ} q_{ν}$ :
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{(- q^{2})^{α} (- (q + k)^{2})^{β}} \\ = (4 π)^{- D / 2} (- k^{2})^{D / 2 - α - β} \frac{Γ (α + β - D / 2)}{Γ (α) Γ (β)} [k^{2} g_{μ ν} \frac{B (D / 2 - α + 1, D / 2 - β + 1)}{2 (α + β - 1 - D / 2)} \\ + k_{μ} k_{ν} B (\frac{D}{2} - α + 2, \frac{D}{2} - β)] \\ = (4 π)^{- (2 - ϵ)} (- k^{2})^{(2 - ϵ) - α - β} \frac{Γ (α + β - (2 - ϵ))}{Γ (α) Γ (β)} [k^{2} g_{μ ν} \frac{B ((2 - ϵ) - α + 1, (2 - ϵ) - β + 1)}{2 (α + β - 1 - (2 - ϵ))} \\ + k_{μ} k_{ν} B ((2 - ϵ) - α + 2, (2 - ϵ) - β)] \end{aligned}$

1.は分母をまとめたのち、Wick rotation・極座標に移ることで $q$ に関して積分し、その後 $x, y$ に関する積分を $B$ 関数で書き直すことで答えを得る。
2.は1.の両辺を $k_{μ}$ で微分することで得られる。
3.は2.の両辺を $k_{ν}$ で微分することで得られる。

つぎの公式も有用です（左辺はWick rotationする前の表式）：

ループ積分の公式2

分子が $1$ ：
$\begin{array}{r} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{(m^{2} + 2 q \cdot p - q^{2})^{a}} = \frac{Γ (a - D / 2)}{(4 π)^{D / 2} Γ (a)} \frac{1}{(m^{2} + p^{2})^{a - D / 2}} \end{array}$
分子が $q$ 1つ：
$\begin{array}{r} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{(m^{2} + 2 q \cdot p - q^{2})^{a}} = \frac{Γ (a - D / 2)}{(4 π)^{D / 2} Γ (a)} \frac{p_{μ}}{(m^{2} + p^{2})^{a - D / 2}} \end{array}$
分子が $q$ 2つ:
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} & \frac{q_{μ} q_{ν}}{(m^{2} + 2 q \cdot p - q^{2})^{a}} \\ = \frac{1}{(4 π)^{D / 2} Γ (a)} [Γ (a - D / 2) \frac{p_{μ} p_{ν}}{(m^{2} + p^{2})^{a - D / 2}} - \frac{1}{2} g_{μ ν} Γ (a - 1 - D / 2) \frac{1}{(m^{2} + p^{2})^{a - 1 - D / 2}}] \end{aligned}$
分子が $q$ 3つ:
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} & \frac{q_{μ} q_{ν} q_{ρ}}{(m^{2} + 2 q \cdot p - q^{2})^{a}} \\ = \frac{1}{(4 π)^{D / 2} Γ (a)} [Γ (a - D / 2) \frac{p_{μ} p_{ν} p_{ρ}}{(m^{2} + p^{2})^{a - D / 2}} - \frac{1}{2} g_{(μ ν} p_{ρ)} Γ (a - 1 - D / 2) \frac{1}{(m^{2} + p^{2})^{a - 1 - D / 2}}] \end{aligned}$
分子が $q$ 4つ:
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} & \frac{q_{μ} q_{ν} q_{ρ} q_{σ}}{(m^{2} + 2 q \cdot p - q^{2})^{a}} \\ = \frac{1}{(4 π)^{D / 2} Γ (a)} [Γ (a - D / 2) \frac{p_{μ} p_{ν} p_{ρ} p_{σ}}{(m^{2} + p^{2})^{a - D / 2}} - \frac{1}{2} g_{(μ ν} p_{ρ} p_{σ)} Γ (a - 1 - D / 2) \frac{1}{(m^{2} + p^{2})^{a - 1 - D / 2}} \\ + \frac{1}{4} g_{(μ ν} g_{ρ σ)} Γ (a - 2 - D / 2) \frac{1}{(m^{2} + p^{2})^{a - 2 - D / 2}}] \end{aligned}$

ただし
$\begin{aligned} g_{(μ ν} p_{ρ)} & := g_{μ ν} p_{ρ} + g_{ν ρ} p_{μ} + g_{ρ μ} p_{ν}, \\ g_{(μ ν} p_{ρ} p_{σ)} & := g_{μ ν} p_{ρ} p_{σ} + g_{μ ρ} p_{ν} p_{σ} + g_{μ σ} p_{ν} p_{ρ} + g_{ν ρ} p_{μ} p_{σ} + g_{ν σ} p_{μ} p_{ρ} + g_{ρ σ} p_{μ} p_{ν}, \\ g_{(μ ν} g_{ρ σ)} & := g_{μ ν} g_{ρ σ} + g_{μ ρ} g_{ν σ} + g_{μ σ} g_{ν ρ} \end{aligned}$

変数変換し、分母の $q \cdot p$ の項を消す
積分変数のうち、浮いたLorentzのindexを持つものを公式5により消す or 縮約をとる
公式9により積分する

を行えば示せる。

ベータ関数 $B (x, y)$ の性質

ループ積分にはベータ関数が現れます。その性質をまとめておきます。

B (x, y)

に関する公式

$B (p, q) := \int_{0}^{1} d x x^{p - 1} (1 - x)^{q - 1} = \int_{0}^{\infty} \frac{t^{p - 1}}{(1 + t)^{p + q}} d t = \frac{Γ (p) Γ (q)}{Γ (p + q)}$
$B (x, y) = B (y, x)$
$x B (x, y + 1) = y B (x + 1, y)$
$(x + y) B (x, y + 1) = y B (x, y), (x + y) B (x + 1, y) = x B (x, y)$
$B (x, y + 1) = \frac{y}{x + y} B (x, y), B (x + 1, y) = \frac{x}{x + y} B (x, y)$

一番上の式は公式9の1.で示した。
残りの式は $B$ 関数の $Γ$ 関数による表示より導ける。

余談ですが、走る結合定数の計算では、特殊関数のベータ関数とは関係のない「ベータ（ $β$ ）関数＝結合定数のエネルギースケールによる微分」を扱います。混乱しないようにしてください。

$B$ 関数を $B (2 - ϵ, 2 - ϵ)$ に書き換える

以下は一般的に必要な公式ではなく、Ref.[1]で行われる変形に必要なものです。本記事はこれに習います。

B (2 - ϵ, 2 - ϵ)

に書き変える

$B (1 - ϵ, 1 - ϵ) = \frac{2 (3 - 2 ϵ)}{1 - ϵ} B (2 - ϵ, 2 - ϵ)$
$B (3 - ϵ, 1 - ϵ) = \frac{2 - ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ)$
$B (2 - ϵ, 1 - ϵ) = \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ)$
$B (- ϵ, 1 - ϵ) = - \frac{2 (3 - 2 ϵ) (1 - 2 ϵ)}{ϵ (1 - ϵ)} B (2 - ϵ, 2 - ϵ)$
$B (3 - ϵ, - ϵ) = - \frac{(3 - 2 ϵ) (2 - ϵ)}{ϵ (1 - ϵ)} B (2 - ϵ, 2 - ϵ)$
$B (2 - ϵ, - ϵ) = - \frac{2 (1 - ϵ) (3 - 2 ϵ)}{ϵ (1 - ϵ)} B (2 - ϵ, 2 - ϵ)$

書き換えるだけ

有用な積分の公式

以下は、ファインマン・ダイアグラムの表式に現れるさまざまな積分を、
$P (k^{2}, ϵ) := (4 π)^{- (2 - ϵ)} (- k^{2})^{- ϵ} Γ (ϵ) \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ)$
に比例した形で書き直す公式です。次回の記事ではこの表記を用います。

以下では次のnotationを用います： $M (α, β; x) := \frac{x}{(q^{2})^{α} ((q + k)^{2})^{β}}$
たとえば次の例のようになります。
$\begin{array}{r} {\begin{cases} M (1, 1; 1) = \frac{1}{q^{2} (q + k)^{2}}, \\ M (1, 2; q_{μ}) = \frac{q_{μ}}{q^{2} ((q + k)^{2})^{2}}, \\ M (2, 2; q_{μ} q_{ν}) = \frac{q_{μ} q_{ν}}{(q^{2}) ((q + k)^{2})^{2}}, \\ M (1, 1,; L_{μ ν}) = \frac{q_{μ} k_{ν} + q_{ν} k_{ν}}{(q^{2}) ((q + k)^{2})^{2}} \end{cases} \end{array}$
ただし $L_{μ ν} := q_{μ} k_{ν} + q_{ν} k_{ν}$ とします。

$M (1, 1; 1)$ の積分
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{q^{2} (q + k)^{2}} & = (4 π)^{- (2 - ϵ)} (- k^{2})^{- ϵ} Γ (ϵ) B (- ϵ, 1 - ϵ) \\ = (4 π)^{- (2 - ϵ)} (- k^{2})^{- ϵ} \frac{2 (3 - 2 ϵ)}{1 - ϵ} Γ (ϵ) B (2 - ϵ, 2 - ϵ) \\ = 2 P (k^{2}, ϵ), \end{aligned}$
$M (1, 2; 1)$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{q^{2} ((q + k)^{2})^{2}} & = (4 π)^{- (2 - ϵ)} (- k^{2})^{- 1 - ϵ} Γ (ϵ) \frac{2 (1 - 2 ϵ) (3 - 2 ϵ)}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = 2 (1 - 2 ϵ) \frac{1}{- k^{2}} P (k^{2}, ϵ) \end{aligned}$
$M (2, 1; 1)$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{(q^{2})^{2} (q + k)^{2}} & = (4 π)^{- (2 - ϵ)} (- k^{2})^{- 1 - ϵ} Γ (ϵ) \frac{2 (1 - 2 ϵ) (3 - 2 ϵ)}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = 2 (1 - 2 ϵ) \frac{1}{- k^{2}} P (k^{2}, ϵ) \\ (= \int \frac{d^{D} q}{(2 π)^{D} i} \frac{1}{(q^{2}) ((q + k)^{2})^{2}}) \end{aligned}$
$M (1, 1; q_{μ})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{q^{2} (q + k)^{2}} & = - (4 π)^{- (2 - ϵ)} k_{μ} (- k^{2})^{- ϵ} Γ (ϵ) B (2 - ϵ, 1 - ϵ) \\ = - (4 π)^{- (2 - ϵ)} k_{μ} (- k^{2})^{- ϵ} \frac{3 - 2 ϵ}{1 - ϵ} Γ (ϵ) B (2 - ϵ, 2 - ϵ) \\ = - k_{μ} P (k^{2}, ϵ) \end{aligned}$
$M (1, 2; q_{μ})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{q^{2} ((q + k)^{2})^{2}} & = - (4 π)^{- (2 - ϵ)} k_{μ} (- k^{2})^{- 1 - ϵ} Γ (ϵ) \frac{2 (3 - 2 ϵ) (1 - ϵ)}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = 2 (1 - ϵ) \frac{k_{μ}}{k^{2}} P (k^{2}, ϵ) \end{aligned}$
$M (2, 1; q_{μ})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ}}{(q^{2})^{2} (q + k)^{2}} & = - (4 π)^{- (2 - ϵ)} k_{μ} (- k^{2})^{- 1 - ϵ} ϵ Γ (ϵ) \frac{2 (3 - 2 ϵ)}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = - 2 ϵ \frac{k_{μ}}{k^{2}} P (k^{2}, ϵ) \end{aligned}$
$M (1, 1; q_{μ} q_{ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{q^{2} (q + k)^{2}} & = - (4 π)^{- (2 - ϵ)} (- k^{2})^{- ϵ} Γ (ϵ) {\frac{1}{2} k^{2} g_{μ ν} - (2 - ϵ) k_{μ} k_{ν}} \frac{1}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = - \frac{1}{3 - 2 ϵ} {\frac{1}{2} k^{2} g_{μ ν} - (2 - ϵ) k_{μ} k_{ν}} P (k^{2}, ϵ) \end{aligned}$
$M (1, 2; q_{μ} q_{ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{q^{2} ((q + k)^{2})^{2}} & = - (4 π)^{- (2 - ϵ)} (- k^{2})^{- 1 - ϵ} Γ (ϵ) {\frac{1}{2} k^{2} g_{μ ν} - (2 - ϵ) k_{μ} k_{ν}} \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = \frac{1}{k^{2}} {\frac{1}{2} k^{2} g_{μ ν} - (2 - ϵ) k_{μ} k_{ν}} P (k^{2}, ϵ) \end{aligned}$
$M (2, 1; q_{μ} q_{ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{(q^{2})^{2} (q + k)^{2}} & = - (4 π)^{- (2 - ϵ)} (- k^{2})^{- 1 - ϵ} Γ (ϵ) {\frac{1}{2} k^{2} g_{μ ν} + ϵ k_{μ} k_{ν}} \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = \frac{1}{k^{2}} {\frac{1}{2} k^{2} g_{μ ν} + ϵ k_{μ} k_{ν}} P (k^{2}, ϵ) \end{aligned}$
$M (2, 2; q_{μ} q_{ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} q_{ν}}{(q^{2})^{2} ((q + k)^{2})^{2}} & = (4 π)^{- (2 - ϵ)} (- k^{2})^{(2 - ϵ)} Γ (ϵ) {ϵ k^{2} g_{μ ν} - 2 k_{μ} k_{ν} (1 - ϵ) (1 + ϵ)} \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = \frac{1}{(k^{2})^{2}} {ϵ k^{2} g_{μ ν} - 2 k_{μ} k_{ν} (1 - ϵ) (1 + ϵ)} P (k^{2}, ϵ) \end{aligned}$
$M (1, 1; L_{μ ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{μ} k_{ν} + q_{ν} k_{μ}}{q^{2} (q + k)^{2}} & = - (k_{μ} k_{ν} + k_{ν} k_{μ}) P (k^{2}, ϵ) \end{aligned}$
$M (1, 2; q_{ρ} L_{μ ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{ρ} (q_{μ} k_{ν} + q_{ν} k_{μ})}{q^{2} ((q + k)^{2})^{2}} & = \frac{1}{k^{2}} [{\frac{1}{2} k^{2} g_{ρ μ} - (2 - ϵ) k_{ρ} k_{μ}} k_{ν} + {\frac{1}{2} k^{2} g_{ρ ν} - (2 - ϵ) k_{ρ} k_{ν}} k_{μ}] P (k^{2}, ϵ) \end{aligned}$
$M (2, 1; q_{ρ} L_{μ ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{ρ} (q_{μ} k_{ν} + q_{ν} k_{μ})}{(q^{2})^{2} (q + k)^{2}} & = \frac{1}{k^{2}} [{\frac{1}{2} k^{2} g_{ρ μ} + ϵ k_{ρ} k_{μ}} k_{ν} + {\frac{1}{2} k^{2} g_{ρ ν} + ϵ k_{ρ} k_{ν}} k_{μ}] P (k^{2}, ϵ) \end{aligned}$
$M (2, 2; q_{ρ} L_{μ ν})$
$\begin{aligned} \int \frac{d^{D} q}{(2 π)^{D} i} \frac{q_{ρ} (q_{μ} k_{ν} + q_{ν} k_{μ})}{(q^{2})^{2} (q + k)^{2}} & = \frac{1}{(k^{2})^{2}} [{ϵ k^{2} g_{ρ μ} - 2 (1 - ϵ^{2}) k_{ρ} k_{μ}} k_{ν} + {ϵ k^{2} g_{ρ ν} - 2 (1 - ϵ^{2}) k_{ρ} k_{ν}} k_{μ}] P (k^{2}, ϵ) \end{aligned}$

本記事に示した公式を用いて計算すれば導ける

$Γ$ 関数、 $B$ 関数の極に関する公式

くりこみではループ積分の $ϵ$ によるLaurent展開が必要です。以下に $Γ$ 関数、 $B$ 関数、および前記の $P (k^{2}, ϵ)$ のLaurent展開を示しておきます。

$ϵ ≪ 1$ のとき

$\begin{array}{r} Γ (ϵ) = \frac{1}{ϵ} - γ + \frac{1}{2} (γ^{2} + \frac{π^{2}}{6}) ϵ + O (ϵ^{2}) \end{array}$
$\begin{array}{r} Γ (- 1 + ϵ) = - \frac{1}{ϵ} + (γ - 1) - \frac{1}{2} (γ^{2} - 2 γ + \frac{π^{2}}{6} + 2) ϵ + O (ϵ^{2}) \end{array}$
$\begin{array}{r} Γ (- N + ϵ) = \frac{(- 1)^{N}}{N!} [\frac{1}{ϵ} + ψ (N + 1) + O (ϵ)] (N : positive integer) \end{array}$
ここで
$\begin{aligned} ψ (x) & \equiv Γ^{'} (x) / Γ (x), \\ ψ (1) & = - γ, ψ (N + 1) = - γ + \sum_{k = 1}^{N} \frac{1}{k}, \\ γ & = - Γ^{'} (1) = 0.5772 \dots \end{aligned}$
$\begin{array}{r} Γ (1 + ϵ) = 1 - γ ϵ + \sum_{k = 2}^{\infty} \frac{(- ϵ)^{k}}{k!} ζ (k) \end{array}$
$\begin{array}{r} (1 - ϵ) B (1 - ϵ, 1 - ϵ) = 1 + γ + O (ϵ^{2}) \end{array}$
$P (k^{2}, ϵ)$ のLaurent展開：
$\begin{aligned} P (k^{2}, ϵ) & := (4 π)^{- (2 - ϵ)} (- k^{2})^{- ϵ} Γ (ϵ) \frac{3 - 2 ϵ}{1 - ϵ} B (2 - ϵ, 2 - ϵ) \\ = \frac{1}{2 (4 π)^{2}} (\frac{1}{ϵ} + \log (\frac{4 π}{- k^{2}}) - γ + 2 + O (ϵ)) \end{aligned}$

$Γ$ 関数は $R e (z) \leq 0$ では収束しないが、部分積分をくりかえすことにより、 $R e (z) < 0$ の領域に
$Γ (z) = \frac{Γ (z + n + 1)}{z (z + 1) \dots (z + n)}$
のように解析接続することができる。これより $z = - n$ のまわりでのLaurent展開が計算できる。
上の式より $Γ$ 関数は $z = - n$ で1位の極をもつ。それぞれの留数は
$lim_{z \to - n} (z + n) Γ (z) = \frac{(- 1)^{n}}{n!}$
である。

$D$ 次元のDirac行列に関する公式

quarkのようなFermionはspinorであり、そのループ積分にはDirac行列 $γ^{μ}$ が現れます。これはLorentz変換に対するspinorとvectorの変換性を結ぶものです。この行列に関する性質をまとめておきます。

D

次元Dirac行列に関して

任意の $D$ 次元における公式(Ref.[3]より):

${γ^{μ}, γ^{ν}} = 2 g^{μ ν} 1$
$g_{μ}^{μ} = D$
$γ_{μ} γ^{μ} = D 1$
$t r (1) = 2^{D / 2}^{(* *)}$
$γ^{μ} γ_{α} γ_{μ} = (2 - D) γ_{α}$
$γ^{μ} γ_{α} γ_{β} γ_{μ} = (D - 4) γ_{α} γ_{β} + 4 g_{α β}$
$γ^{μ} γ_{α} γ_{β} γ_{δ} γ_{μ} = - 2 γ_{δ} γ_{β} γ_{α} - (D - 4) γ_{α} γ_{β} γ_{δ}$
$γ^{μ} σ_{α β} γ_{μ} = (D - 4) σ_{α β}, σ^{μ ν} := \frac{i}{2} [γ^{μ}, γ^{ν}]$
$γ^{μ} σ_{μ α} = i (D - 1) γ_{α}$
$σ_{μ α} γ^{μ} = i (1 - D) γ_{α}$
奇数個の $γ$ 行列のtraceはゼロ
$t r (γ^{μ} γ^{ν}) = 4 g^{μ ν}$
$t r (γ^{μ} γ^{ν} γ^{α} γ^{β}) = 4 (g^{μ ν} g^{α β} - g^{μ α} g^{ν β} + g^{μ β} g^{ν α})$
任意次元の $γ^{5}$ に関する公式に関しては、例えばRef.[2]を参照のこと。

$γ^{μ}$ の反交換関係: ${γ^{μ}, γ^{ν}} = 2 g^{μ ν} 1$ （これは定義）、 $g^{μ ν} g_{μ ν} = g_{μ}^{μ} = D$ や $t r$ の巡回置換不変性等から導ける。
詳細は略。

$D$ 次元の $γ^{μ}$ は何行何列なんだ？等のことは考えず、抽象的に ${γ^{μ}, γ^{ν}} = g^{μ ν} 1$ を満たすもので、縮約や $t r$ 等で足を潰したとき上記公式のように $D$ への依存性が現れる量、と解釈してください。

まとめ

今回は、次元正則化によるダイアグラムの計算、およびくりこみに必要な公式をまとめました。

次回は具体的なダイアグラムの計算を行います。

おしまい。 $_{◼}$

$♣$ 次の記事：走る結合定数の計算(4/5): Yang-Mills理論におけるくりこみの具体的な計算

$(*)$ Euclidにおける運動量積分は正当化が難しいため、これをMinkowski時空で行う方法もあります。例えばRef.[2]のP79-を参照のこと。
$(* *)$ Ref.[3]では $t r (1) = 4$ を採用していますが、 $t r (1) = 2^{D / 2}$ を採用している教科書が多いので、こちらを載せました。

Appendix: 公式4の2.の証明

改めて公式4の2.を記しておきます：

$\frac{1}{A_{1} \dots A_{N}} = Γ [N] \int_{0}^{1} d x_{1} \dots d x_{N} δ (1 - \sum_{j = 1}^{N} x_{j}) \frac{1}{[A_{1} x_{1} + \dots + A_{N} x_{N}]^{N}}$

以下Ref.[4]P86に従い証明します。

まず
$\frac{1}{A^{N}} = (Γ (N))^{- 1} \int_{0}^{\infty} d t t^{N - 1} e^{A t}$
であることに注意します。
（ $Γ$ 関数の定義 $Γ (N) = \int_{0}^{\infty} d t t^{N - 1} e^{- t}$ において $t = A \tilde{t}$ と変数変換すると得られる）。

公式4の2.の右辺
$\begin{array}{r} Γ (N) \int_{0}^{1} d x_{1} \dots d x_{N} δ (1 - \sum_{j = 1}^{N} x_{j}) \frac{1}{(A_{1} x_{1} + \dots + A_{N} x_{N})^{N}} \end{array}$
は、Eq.(A-1)と $δ (1 - \sum_{j = 1}^{N} x_{j}) = \int_{- \infty}^{\infty} \frac{d λ}{2 π} e^{i λ (1 - \sum_{j = 1}^{N} x_{j})}$ および $\int_{0}^{1} d x_{i} e^{- A_{i} x_{i} t - i λ x_{i}} = \frac{1}{- A_{i} t - i λ} (e^{- A_{i} t - i λ} - 1)$ を用いて
$\begin{array}{r} = \int_{0}^{\infty} d t t^{N - 1} \frac{1}{2 π i^{N}} \int_{- \infty}^{\infty} \frac{d λ}{2 π} e^{i λ} \prod_{j} \frac{1 - e^{- A_{j} t - i λ}}{- i A_{j} t + λ} \end{array}$
となります。
以下 $A_{j} > 0$ とします（負の $A_{j}$ があるときは公式4の2.の左辺でマイナスをくくりだし正にして扱う）。このとき、被積分関数のpole $λ = i A_{j} t$ は全て上半平面に存在します。

下半平面の経路による積分。!FORMULA[308][-402136925][0]は半径無限大の半円の経路。オレンジのバツはpoleの位置。下半平面の経路による積分。 $C_{2}^{-}$ は半径無限大の半円の経路。オレンジのバツはpoleの位置。

ここで被積分関数の $e^{i λ} (1 - e^{- A_{1} t - i λ}) \times \dots \times e^{i λ} (1 - e^{- A_{N} t - i λ})$ を展開した項のうち、 $e^{- i k λ} (k = 1, \dots, N - 1)$ がかかる項の積分は、図3のように下半面に積分を閉じたとき、半円 $C_{2}^{-}$ の寄与は０になります。また $C_{1} + C_{2}^{-}$ の中にpoleはないので、結局 $C_{1}$ の積分は消えます。故に残る積分は
$e^{i λ} - \sum_{j = 1}^{N} e^{- A_{j} t}$
の項のみです。よって
$= \int_{0}^{\infty} d t t^{N - 1} \frac{1}{2 π i^{N}} \int_{- \infty}^{\infty} d λ \frac{e^{i λ} - \sum_{j = 1}^{N} e^{- A_{j} t}}{(λ - i t A_{1}) \dots (λ - i t A_{N})}$
この積分を評価するため、次の事実を用います：

$\begin{matrix} (A-2) & \oint d z \frac{1}{(z - α_{1}) (z - α_{2}) \dots (z - α_{r})} = 0 (2 \leq r < \infty) \end{matrix}$
ただし積分経路は全てのpoleを含むように閉じる。

帰納法を用いる。

$r = 2$ のとき
$\begin{array}{r} \oint d z \frac{1}{(z - α_{1}) (z - α_{2})} \end{array}$
は2つのpoleの寄与が逆符号で大きさが等しいので0。
$r = k$ で成立を仮定したとき、 $r = k + 1$ では
$\begin{array}{r} \oint d z \frac{1}{(z - α_{1}) \dots (z - α_{k}) (z - α_{k + 1})} \\ = \oint d z (\frac{1}{(z - α_{1}) (z - α_{2}) \dots (z - α_{k})} - \frac{1}{(z - α_{2}) (z - α_{3}) \dots (z - α_{k + 1})}) \frac{1}{α_{1} - α_{k + 1}} \end{array}$
となるので、 $r = k$ の場合に帰着し0。

以上より題意は示された。 $_{◼}$

定理1よりEq.(A-2)の $\frac{\sum_{j = 1}^{N} e^{- A_{j} t}}{(λ - i t A_{1}) \dots (λ - i t A_{N})}$ の寄与は消えます。

ここまでをまとめると
$(公式4の2.の右辺) = \int_{0}^{\infty} d t t^{N - 1} \frac{1}{2 π i^{N}} \int_{- \infty}^{\infty} d λ \frac{e^{i λ}}{(λ - i t A_{1}) \dots (λ - i t A_{N})}$
が得られました。これを図4の経路で積分します:

上半平面の経路による積分。!FORMULA[325][-402136987][0]は半径無限大の半円の経路。オレンジのバツはpoleの位置。上半平面の経路による積分。 $C_{2}^{+}$ は半径無限大の半円の経路。オレンジのバツはpoleの位置。

$\begin{aligned} \int_{0}^{\infty} d t t^{N - 1} \frac{1}{2 π i^{N}} \int_{- \infty}^{\infty} d λ \frac{e^{i λ}}{(λ - i t A_{1}) \dots (λ - i t A_{N})} \\ = \int_{0}^{\infty} d t t^{N - 1} \frac{1}{2 π i^{N}} \oint_{C_{1} + C_{2}^{+}} d λ \frac{e^{i λ}}{(λ - i t A_{1}) \dots (λ - i t A_{N})} (∵ contribution from C_{2}^{+} vanishes) \\ = \int_{0}^{\infty} d t t^{N - 1} \frac{2 π i}{2 π i^{N}} [{\sum_{j} \frac{e^{i λ}}{\prod_{i \neq j} (λ - i t A_{i})} |}_{λ = i t A_{j}}] \\ = \int_{0}^{\infty} d t t^{N - 1} (- 1)^{N - 1} \sum_{j} \frac{e^{- t A_{j}}}{\prod_{i \neq j} (A_{j} - A_{i})} \\ = \sum_{j} \frac{(- 1)^{N - 1}}{A_{j} \prod_{i \neq j} (A_{j} - A_{i})} \end{aligned}$

さらに以下が成立することを用います：

$\begin{array}{r} \sum_{j = 1}^{N} \frac{1}{A_{j}} \frac{(- 1)^{N - 1}}{\prod_{i \neq j} (A_{j} - A_{i})} = \frac{1}{A_{1} \dots A_{N}} \end{array}$

Eq.(A-2)において $α_{1} \to 0, α_{2} \to 1, \dots, α_{r} \to A_{N}$ とすると
$\begin{array}{r} \oint d z \frac{1}{z (z - A_{1}) \dots (z - A_{N})} = 0 \end{array}$
これを書き換えれば
$\begin{aligned} 2 π i {\frac{(- 1)^{N}}{A_{1} \dots A_{N}} + \frac{1}{A_{1} (A_{1} - A_{2}) \dots (A_{1} - A_{N})} + \frac{1}{A_{2} (A_{2} - A_{1}) \dots (A_{2} - A_{N})} + \dots} = 0 \\ \leftrightarrow \frac{(- 1)^{N}}{A_{1} \dots A_{N}} + \sum_{j = 1}^{N} \frac{1}{A_{j}} \frac{1}{\prod_{i \neq j} (A_{j} - A_{i})} = 0 \end{aligned}$
これは定理2と等しい。

定理2の右辺は「公式4の2.の左辺」です。よって「公式4の2.の右辺=公式4の2.の左辺」が成立し、題意が示されました。 $_{◼}$

参考文献

[1]

T. Muta, Foundation of Quantum Chromodynamics (Third edition), World Scientific Lecture Notes in Physics, World Scientific, 2009

[2]

九後汰一郎, ゲージ場の量子論 I, 新物理学シリーズ 23, 培風館, 1989

[3]

Appendix, 閲覧日 2022年8月3日, https://cds.cern.ch/record/1201501/files/978-3-540-48535-3_BookBackMatter.pdf

[4]

柏太郎, 演習くり込み群確かな理解と習得を目指して, 臨時別冊数理科学 SGCライブラリ 61, サイエンス社, 2008

投稿日：2022年8月3日

更新日：2024年3月26日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

bisaitama

142

65040

他の人のコメント

コメントはありません。

読み込み中

bisaitama

走る結合定数の計算(3/5): 摂動計算に関する数学公式集

はじめに
公式集
ゲージ群の生成子に関わる公式
$i ϵ$ 処方、Feynman prescription
次元正則化
被積分関数の分母をまとめる： Feynman parametrization
対称性から導かれる公式
虚時間方向への積分路の変更
$D$ 次元の極座標表示
分母がまとまっている場合のループ積分
$D$ 次元における物理量の次元解析
ループ積分の公式
ベータ関数 $B (x, y)$ の性質
$B$ 関数を $B (2 - ϵ, 2 - ϵ)$ に書き換える
有用な積分の公式
$Γ$ 関数、 $B$ 関数の極に関する公式
$D$ 次元のDirac行列に関する公式
まとめ
Appendix: 公式4の2.の証明
参考文献

走る結合定数の計算(3/5): 摂動計算に関する数学公式集

はじめに

公式集

ゲージ群の生成子に関わる公式

iϵ処方、Feynman prescription

次元正則化

被積分関数の分母をまとめる： Feynman parametrization

対称性から導かれる公式

虚時間方向への積分路の変更

D次元の極座標表示

分母がまとまっている場合のループ積分

D次元における物理量の次元解析

ループ積分の公式

ベータ関数B(x,y)の性質

B関数をB(2−ϵ,2−ϵ)に書き換える

有用な積分の公式

Γ関数、B関数の極に関する公式

D次元のDirac行列に関する公式

まとめ

Appendix: 公式4の2.の証明

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$i ϵ$ 処方、Feynman prescription

$D$ 次元の極座標表示

$D$ 次元における物理量の次元解析

ベータ関数 $B (x, y)$ の性質

$B$ 関数を $B (2 - ϵ, 2 - ϵ)$ に書き換える

$Γ$ 関数、 $B$ 関数の極に関する公式

$D$ 次元のDirac行列に関する公式