走る結合定数の計算(4/5): Yang-Mills理論におけるくりこみの具体的な計算

16Aug.2022: 「まとめ」の章の$Z_g$の表式が間違っていました。 $Z_g={\tilde Z_1}/({\tilde Z}_3 Z_3^{1/2})$が正しいです（1/2乗が抜けてました）。

★ 本記事は 走る結合定数の計算(3/5):摂動計算に関する数学公式集 の続きです。
★ 本記事で用いる表記の規約に関しては 走る結合定数の計算(2/5):Yang-Mills理論のくりこみ の冒頭をご参照ください。
★ 本記事はRef.[1]を元に書かれています。
★ 計算の正しさについて： 各くりこみ定数はRef.[1]の結果と一致しています。細かい計算に関しては文献との比較はしておりませんのでご了承ください。
★ 計算の一部は、微分幾何学におけるテンソル算のMathematicaライブラリ xAct 、および場の量子論計算用Mathematicaライブラリ FeynCalc (Ref.[2-4])を使用しています。
★ 「公式」とは基本的に 前回記事 の公式を指します

はじめに

Yang-Mills(YM)理論における走る結合定数の計算の第4回です。

今回は具体的な計算を実行します。前々回の記事のFeynman則、および前回の記事で示した公式を使いますので、適宜参照してください。Feynman則は本記事のAppendixにも掲載しておきます。

計算の概要

第２回で述べたとおり、走る結合定数の計算には、結合定数の繰り込み定数$Z_g$が必要になります。本記事の目的は
「$Z_g$を計算すること」
です。

これを計算する方法は4つほどありますが、そのうち

を用います。ここで改めて用語を説明しおくと

• $n$点関数: $n$本の外線（外に出ている線）を持つダイアグラム
• 1PI（one particle irreducible、1粒子既約）ダイアグラム: 内線（外線ではない線）を切っても2つの部分に分かれないダイアグラム
• 頂点関数: 外線をもぎとったダイアグラム（vertex因子は残しておく）

です。よって、たとえば「ghost-ghost-gluon3点1PI頂点関数」とは 「ghostの外線が2つ、gluonの外線がひとつ出ている1PIダイアグラムから外線をもぎとったダイアグラム」です。

本記事では$g^2$のオーダーで$Z_g$を評価します。これに必要な1PI頂点関数を図1に示します：

結合定数の2次のオーダーで$Z_g=\tilde Z_1 /(\tilde Z_3Z_3^{1/2})$の決定に必要なダイアグラム

上から

• $Z_3$を決定するために評価するダイアグラム=gluonの2点1PI頂点関数
• $\tilde Z_3$を決定するために評価するダイアグラム=ghostの2点1PI頂点関数
• $\tilde Z_1$を決定するために評価するダイアグラム=ghost-ghost-gluon3点1PI頂点関数

です。

$Z_3,\tilde Z_3, \tilde Z_1$はcounter termに含まれています。これらのくりこみ定数は、ダイアグラムの発散部分を打ち消すように決定します。よって、上記のダイアグラムの発散部分を計算することが、本記事の主な作業になります。発散部分の除去には任意性がありますが、ここでは発散部分のみを打ち消す"minimal subtraction (MS) scheme"によりくりこみ定数を決定します。

$Z_3$の評価: gluonの2点1PI頂点関数のくりこみ定数の計算

$g^2$のオーダーにおけるgluon 2点1PI頂点関数

$Z_3$を決定するため、図2のダイアグラムを計算していきます。

Ghost loop contribution

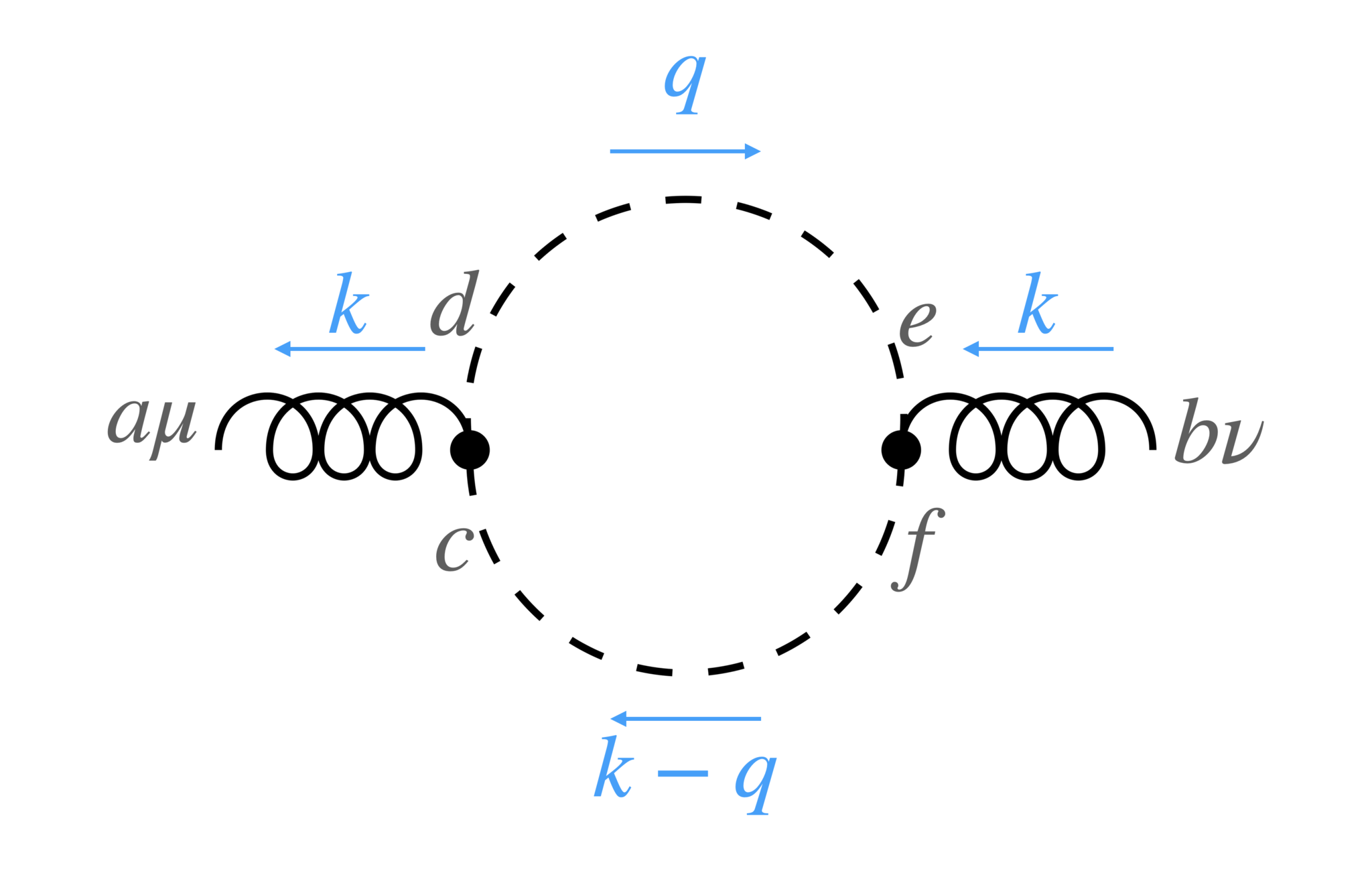ghost loop

まずは簡単な図3のghost loopのダイアグラム$\Pi^{ab}_{{\rm Gh}\mu\nu}$から計算します。図の水色の文字と矢印は、4元運動量とその方向です。運動量保存則はvertexごとにすでに課されています。$a,b,c$等アルファベットはゲージ群のindex、$\mu,\nu,\rho$等ギリシャ文字はLorentzのindexです。

図3はFeynman則より
\begin{align} \Pi^{ab}_{{\rm Gh} \mu\nu}&=-\int \frac{d^Dq}{(2\pi)^Di} \delta^{de} \frac{-1}{q^2} \delta^{cf} \frac{-1}{(k-q)^2} (-ig) f^{acd} q_\mu (-ig) f^{bef} (q-k)_\nu\\ &= g_r^2f^{acd}f^{bdc} \int \frac{d^D q}{(2\pi)^Di} \frac{1}{q^2} \frac{1}{(k-q)^2} q_\mu (q-k)_\nu \end{align}
となります。すでに次元正則化が施してあり、また$i\epsilon$は省略しています。結合定数がくりこまれた結合定数$g_r$なのは、ダイアグラムの計算はrenormalizedなパラメータを伴ったLagrangianで行い、その発散をcounter termで除去する（第１回・第２回の記事参照のこと）ためです。

前回示した公式15を使うとこの計算はすぐできるのですが、このダイアグラムのみ計算過程を示しておきます。この積分は以下のように計算されます：

これを前回の記事で定義した
$$ P(k^2,\epsilon):=(4\pi)^{-(2-\epsilon)} (-k^2)^{\epsilon} \Gamma(\epsilon) B(2-\epsilon,2-\epsilon) \frac{3-2\epsilon}{1-\epsilon} $$
で書き下せば、最終的に
$$ \int\frac{d^Dq}{(2\pi)^Di} \frac{1}{q^2} \frac{1}{(k-q)^2}q_\mu (q-k)_\nu = -\frac{P(k^2,\epsilon)}{3-2\epsilon} \left(\frac{1}{2}k^2g_{\mu\nu}+(1-\epsilon)k_\mu k_\nu\right) \tag{1} $$
を得ます。これに$g_r^2f^{acd}f^{bdc}=-g_r^2\delta_{ab} C_G \ \ (C_G:=N)$をかけると$\Pi^{ab}_{{\rm Gh}\mu\nu}$になります。

以上より図3のダイアグラムの寄与は以下です：

一方で、公式15を使うと
\begin{align} \int\frac{d^Dq}{(2\pi)^Di} \frac{1}{q^2} \frac{1}{(k-q)^2}q_\mu (q-k)_\nu &= \int\frac{d^Dq}{(2\pi)^Di} \frac{q_\mu q_\nu}{q^2(k-q)^2} -k_\nu \int\frac{d^Dq}{(2\pi)^Di} \frac{q_\mu}{q^2(k-q)^2}\\ &= \int\frac{d^Dq}{(2\pi)^Di} \frac{q_\mu q_\nu}{q^2(k+q)^2} +k_\nu \int\frac{d^Dq}{(2\pi)^Di} \frac{q_\mu}{q^2(k+q)^2}\\ &=M(1,1;q_\mu q_\nu) +k_\nu M(1,1;q_\mu)\\ &=-\frac{1}{3-2\epsilon} \left(\frac{1}{2}k^2g_{\mu\nu}-(2-\epsilon)k_\mu k_\nu\right)P(k^2,\epsilon) +k_\nu(-k_\mu P(k^2,\epsilon))\\ &=\text{Eq.}(1) \end{align}
になり、上記計算と一致します。

Gluon tadpole loop contribution

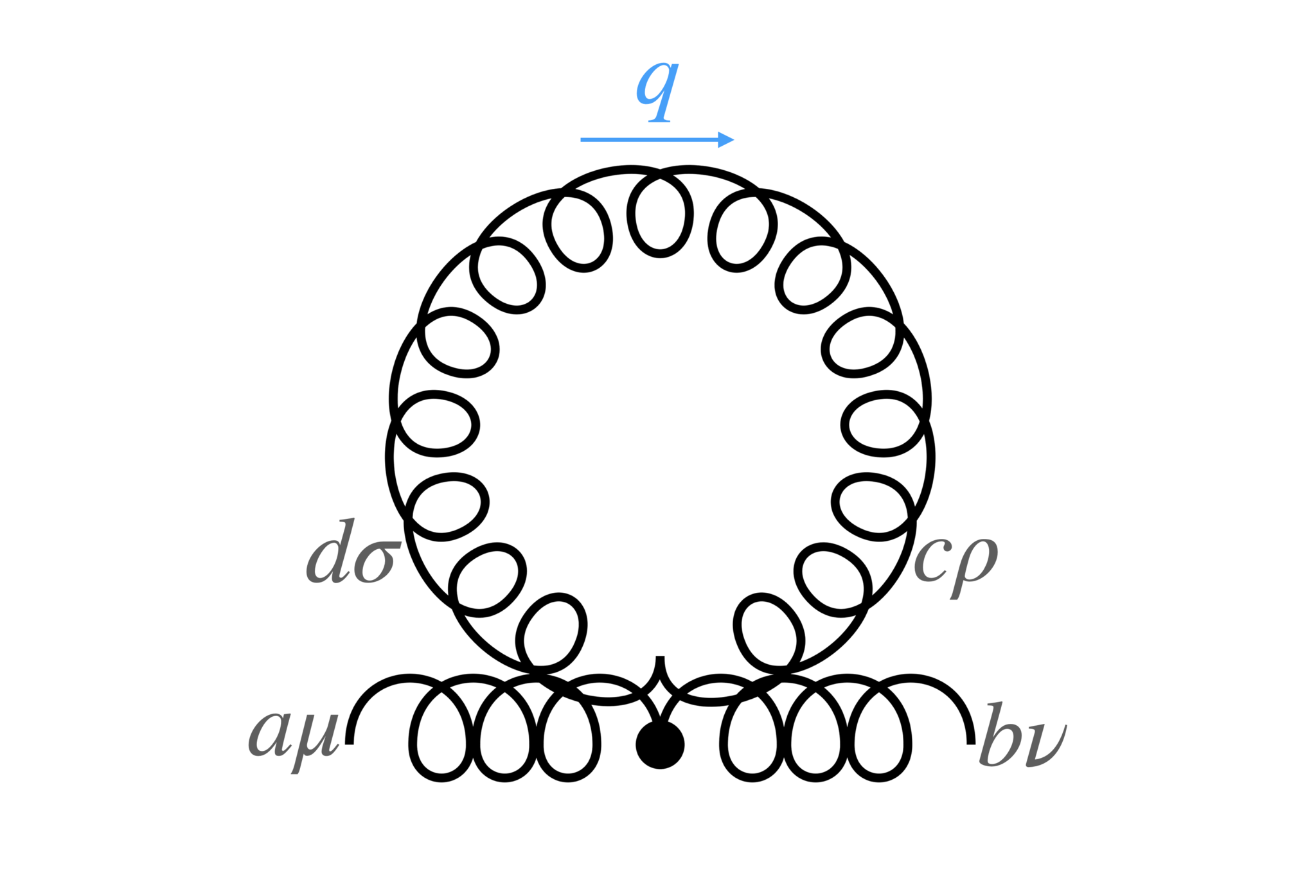tadpole loop

図4のダイアグラム$\Pi^{ab}_{T\mu\nu}$はtadpole loopと呼ばれます。Feynman則より
\begin{align*} \Pi^{ab}_{T\mu\nu}(q) =\frac{1}{2!}\int \frac{d^D q}{(2\pi)^Di} (-g^2)W^{abcd}_{\mu\nu\rho\sigma} \frac{\delta^{cd}}{q^2} d^{\rho\sigma}(q) \end{align*}
です。ここで$1/2!$のファクターは対称因子と呼ばれるものです。これは他のダイアグラムとの相対的な重みを調整するファクターですが、ここでは詳しい説明はしません。

ちょっとした計算ののち、
\begin{align} \Pi^{ab}_{T\mu\nu}(k)= -\frac{g_r^2}{2} \int\frac{d^Dq}{(2\pi)^Di}\delta^{ab}C_G \frac{1}{q^2} \left\{ (D-1)g_{\mu\nu}-(1-\alpha_r)\left(g_{\mu\nu}-\frac{q_\mu q_\nu}{q^2}\right) \right\} \end{align}
であることがわかります。公式5の2.より
\begin{align} \int\frac{d^D q}{(2\pi)^D i} \frac{1}{q^2} \frac{q_\mu q_\nu}{q^2} = \frac{g_{\mu\nu}}{D} \int \frac{d^Dq}{(2\pi)^Di} \frac{1}{q^2}, \end{align}
です。よって$\Pi^{ab}_{T\mu\nu}(k)$は$\displaystyle \int\frac{d^D q}{(2\pi)^Di}\frac{1}{q^2}$に比例しますが、これは公式6よりゼロです。よって

Gluon loop

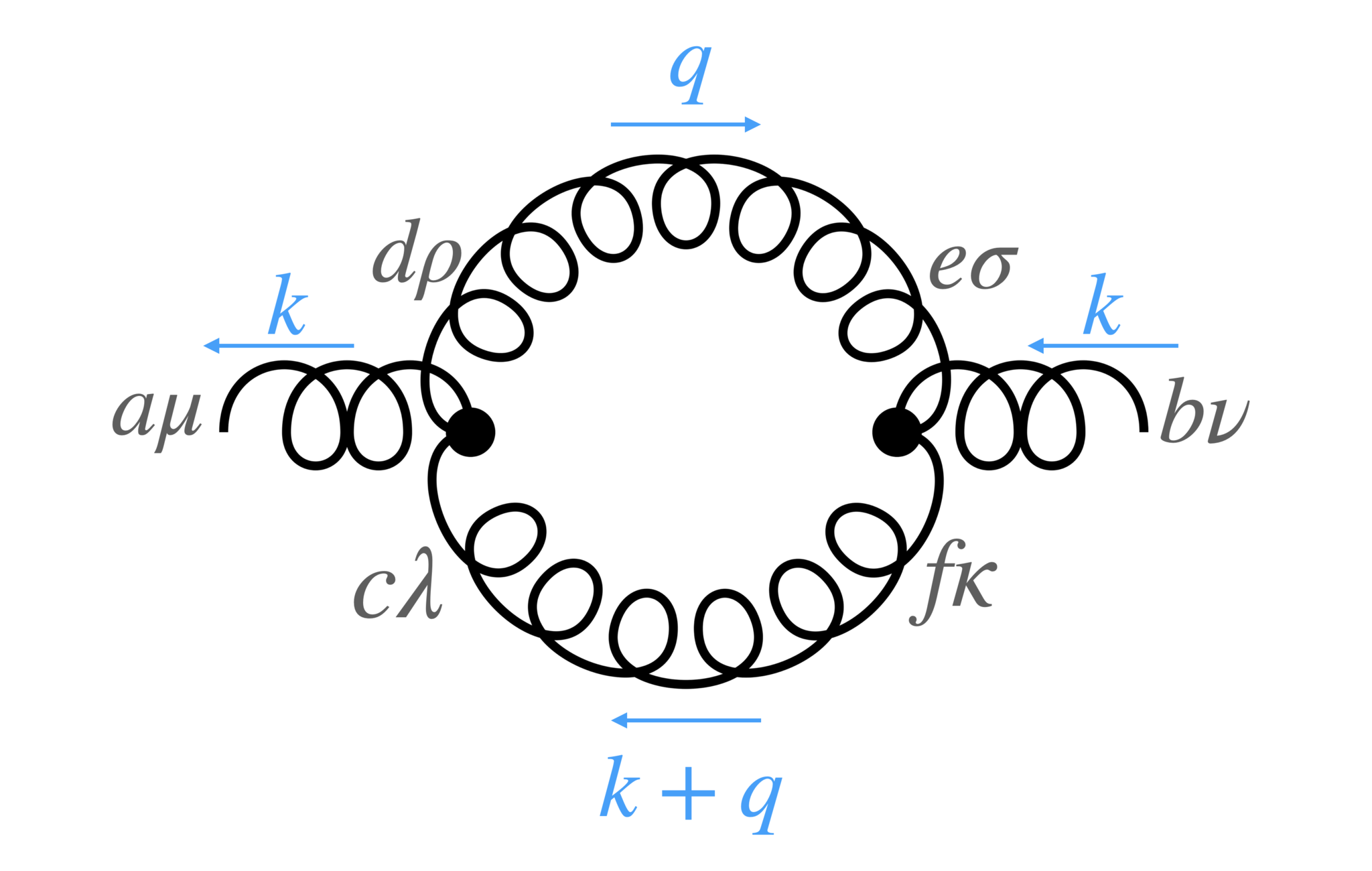gluon loop

図5のダイアグラム$\Pi^{ab}_{G\mu\nu}$を計算します。Feynman則より
\begin{align} \Pi^{ab}_{G\mu\nu} &= \frac{1}{2!} \int \frac{d^D q}{(2\pi)^Di} (-i)g_rf^{acd}V_{\mu\lambda \rho}(-k,q+k,-q)\frac{d^{\lambda\kappa}(q+k)}{(q+k)^2}\frac{d^{\rho\sigma}(q)}{q^2}(-i)g_rf^{bdc}V_{\nu\sigma\kappa}(k,q,-q-k)\\ &= \frac{g_r^2}{2}f^{acd}f^{bcd} \int \frac{d^D q}{(2\pi)^Di} \frac{1}{q^2(q+k)^2}F(q,k) \end{align}
を得ます。$1/2!$は対称因子です。
$F(q,k)$は以下の項からなります。:

上の表式において下線が引いてある項は、前回の公式5・6により消えます。

上記積分の計算を進めます：
\begin{align} \Pi^{ab}_{G\mu\nu}&=\frac{g_r^2}{2}f^{acd}f^{bcd} \Bigg[ \int \frac{d^D q}{(2\pi)^Di} \frac{g_{\mu\nu}}{q^2(q+k)^2} \left( 5k^2 + 2k\cdot q -\frac{(1-\alpha_r)}{(q+k)^2}(k^2)^2 -\frac{4(1-\alpha_r)}{q^2}(k\cdot q)^2 -4(k\cdot q)(1-\alpha_r) \right) \\ &+ \int \frac{d^D q}{(2\pi)^Di} \frac{k_\mu k_\nu}{q^2(q+k)^2} \left( (-6+D) +\frac{(1-\alpha_r)}{(k+q)^2}k^2 -(1-\alpha_r) +\frac{(k\cdot q)^2}{(k+q)^2q^2}(1-\alpha_r)^2 \right) \\ &+ \int \frac{d^D q}{(2\pi)^Di} \frac{q_\mu k_\nu+ q_\nu k_\mu}{q^2(q+k)^2} \left( (-3+2D) +\frac{(1-\alpha_r)}{(k+q)^2}k\cdot q +\frac{(1-\alpha_r)}{q^2}3k\cdot q +(1-\alpha_r) -\frac{k^2(k\cdot q)}{(k+q)^2 q^2}(1-\alpha_r)^2 \right)\\ &+ \int \frac{d^D q}{(2\pi)^Di} \frac{q_\mu q_\mu}{q^2(q+k)^2} \left( (-6+4D) -\frac{(1-\alpha_r)}{(q+k)^2}2k^2 -\frac{1-\alpha_r}{q^2}2k^2 +\frac{(1-\alpha_r)^2}{(q+k)^2q^2}(k^2)^2 \right) \Bigg] \end{align}

これを公式15で示した$M$で書き直し、その後$P(k^2,\epsilon)$に比例した形にします：
\begin{align} &=\frac{g_r^2}{2}f^{acd}f^{bcd}\hspace{16cm}\nonumber\\ &\times\Bigg[ g_{\mu\nu} \left\{ 5k^2M(1,1;q^0) +2k^\rho M(1,1;q_\rho) -(1-\alpha_r)(k^2)^2M(1,2;q^0) -4(1-\alpha_r)k^\rho k^\sigma M(2,1;q_\rho q_\sigma) -4k^\rho(1-\alpha_r)M(1,1;q_\rho) \right\} \\ &+k_\mu k_\nu \left\{ (-6+D)M(1,1;q^0) +(1-\alpha_r)k^2M(1,2;q^0) -(1-\alpha_r)M(1,1;q^0) +(1-\alpha_r)^2k^\rho k^\sigma M(2,2;q_\rho q_\sigma) \right\}\\ &+\left\{ (-3+2D)M(1,1;L_{\mu\nu}) +(1-\alpha_r)k^\rho M(1,2;q_\rho L_{\mu\nu}) +3(1-\alpha_r)k^\rho M(2,1;q_\rho L_{\mu\nu}) +(1-\alpha_r)M(1,1;L_{\mu\nu})\qquad \right.\\ &\left. -k^2(1-\alpha_r)^2k^\rho M(2,2;q_\rho L_{\mu\nu}) \right\}\\ &+\left\{ (-6+4D)M(1,1;q_\mu q_\nu) -2k^2(1-\alpha_r)M(1,2;q_\mu q_\nu) -2k^2(1-\alpha_r)M(2,1;q_\mu q_\nu) +(1-\alpha_r)^2(k^2)^2M(2,2;q_\mu q_\nu) \right\} \Bigg]\\ &=\frac{g_r^2}{2}f^{acd}f^{bcd} \Bigg[ M(1,1;q^0) \left( 5k^2g_{\mu\nu}+((-6+D)-(1-\alpha_r))k_\mu k_\nu \right)\\ &+M(1,1;q_\rho)(2-4(1-\alpha_r))g_{\mu\nu}k^\rho +M(1,1;L_{\mu\nu})((-3+2D)+(1-\alpha_r))\\ &+M(1,2;q^0)(-g_{\mu\nu}(1-\alpha_r)(k^2)^2+k_\mu k_\nu (1-\alpha_r)k^2)\\ &-4(1-\alpha_r)g_{\mu\nu}k^\rho k^\sigma M(2,1;q_\rho q_\sigma)_r +3(1-\alpha_r)k^\rho M(2,1;q_\rho L_{\mu\nu}) -2k^2(1-\alpha_r) M(2,1;q_\mu q_\nu)\\ &+k_\mu k_\nu (1-\alpha_r)^2 k^\rho k^\sigma M(2,2;q_\rho q_\sigma) -k^2(1-\alpha_r)^2k^\rho M(2,2;q_\rho L_{\mu\nu}) +(1-\alpha_r)^2(k^2)^2M(2,2;q_\mu q_\nu)\\ &+(1-\alpha_r)k^\rho M(1,2;q_\rho L_{\mu\nu}) -2k^2(1-\alpha_r)M(1,2;q_\mu q_\nu)\\ &+(-6+4D)M(1,1;q_\mu q_\nu) \Bigg]\\ &=\frac{g_r^2}{2}f^{acd}f^{bcd} P(k^2,\epsilon)\\ \times\Bigg[ &2(5k^2g_{\mu\nu}+((-6+D)-(1-\alpha_r))k_\mu k_\nu) \\ &-(2-4(1-\alpha_r))g_{\mu\nu}k^\rho k_\rho -((-3+2D)+(1-\alpha_r)) (k_\mu k_\nu+k_\nu k_\mu) \\ &+(-g_{\mu\nu}(1-\alpha_r)(k^2)^2+k_\mu k_\nu(1-\alpha_r)k^2) 2(1-2\epsilon)\frac{1}{-k^2} \\ &-4(1-\alpha_r)g_{\mu\nu}k^\rho k^\sigma \frac{1}{k^2} \left\{ \frac{1}{2}k^2 g_{\rho\sigma}+\epsilon k_\rho k_\sigma \right\} \\ &+3(1-\alpha_r)k^\rho \frac{1}{k^2} \left\{ \left(\frac{1}{2}k^2 g_{\rho\mu}+\epsilon k_\rho k_\mu\right)k_\nu + \left(\frac{1}{2}k^2 g_{\rho\nu}+\epsilon k_\rho k_\nu\right) k_\mu \right\} \\ &-2k^2(1-\alpha_r) \frac{1}{k^2} \left\{ \frac{1}{2}k^2 g_{\mu\nu}+\epsilon k_\mu k_\nu \right\} \\ &+k_\mu k_\nu(1-\alpha_r)^2k^\rho k^\sigma \frac{1}{(k^2)^2} \{ \epsilon k^2 g_{\rho\sigma} -2k_\rho k_\sigma (1-\epsilon)(1+\epsilon) \}\\ &-k^2(1-\alpha_r)^2k^\rho \frac{1}{(k^2)^2} \left\{ \left( \epsilon k^2 g_{\rho\mu} -2k_\rho k_\mu (1-\epsilon)(1+\epsilon) \right)k_\nu + \left( \epsilon k^2 g_{\rho\nu} -2k_\rho k_\nu (1-\epsilon)(1+\epsilon) \right)k_\mu \right\} \\ &+(1-\alpha_r)^2(k^2)^2 \frac{1}{(k^2)^2} \{ \epsilon k^2 g_{\mu\nu} -2k_\mu k_\nu (1-\epsilon)(1+\epsilon) \} \\ &+(1-\alpha_r)k^\rho \frac{1}{k^2}\left\{ (\frac{1}{2}k^2g_{\rho\mu}-(2-\epsilon) k_\rho k_\mu) k_\nu + (\frac{1}{2}k^2g_{\rho\nu}-(2-\epsilon) k_\rho k_\nu) k_\mu \right\}\\ &-2k^2(1-\alpha_r) \frac{1}{k^2}\left\{ (\frac{1}{2}k^2g_{\mu\nu}-(2-\epsilon) k_\mu k_\nu) \right\} \\ &+(-6+4D) \frac{-1}{3-2\epsilon} \left\{ \frac{1}{2}k^2 g_{\mu\nu} -(2-\epsilon)k_\mu k_\nu \right\} \Bigg] \end{align}

まとめると以下を得ます：

Quark loop contribution

quark loop

図6$\Pi^{ab}_{F\mu\nu}$の計算は少し特殊です。quarkの入ったダイアグラムの計算は、そのpropagatorの形が
$$ \frac{1}{m- \gamma\cdot q} $$
のように分母が運動量の1次であること、またガンマ行列が存在することから、gluonのようなBosonの計算とは少し異なります。ここで$\frac{1}{m-\gamma\cdot q}$とは、分母の行列の逆行列:$(m-\gamma\cdot q)^{-1}$のことです。この表記は便利で、以下のような"分母の有理化"が正当化されます：
\begin{align} \frac{1}{m-\gamma\cdot q}\times \frac{m+\gamma\cdot q}{m+\gamma\cdot q} &=\frac{m+\gamma\cdot q}{(m-\gamma\cdot q)(m+\gamma\cdot q)}\\ &=\frac{m+\gamma\cdot q}{m^2-(\gamma\cdot q)^2}\\ &=\frac{m+\gamma\cdot q}{m^2-q^2} \ \ \ \ \ \ (\{\gamma^\mu,\gamma^\nu\}=2g^{\mu\nu}を用いた) \end{align}
こうすると、形式的に分母の行列が"払えて"、逆行列が計算できます。

Feynman則より、計算すべき式は以下になります:
$$ -N_f\int \frac{d^Dp}{(2\pi)^Di} {\rm tr} \left[ g_r\gamma_\mu T^a \frac{1}{m_r-\gamma\cdot( k+ p)} g_r\gamma_\nu T^b \frac{1}{m_r-\gamma\cdot p} \right] $$

$N_f$はquarkのflavor数${}^{(*)}$、$T^a,T^b$はゲージ群のSU(N)のgeneratorです。上式の${\rm tr}$は、ゲージ群のファクターだけではなく、Dirac行列のそれも含みます（空間としては直積なので、それぞれ別に計算してかければいいです）。Dirac行列の${\rm tr}$に関しては公式17を使うと以下を得ます：　
$$ =-N_f{\rm tr}(T^aT^b)g_r^2 \int\frac{d^Dp}{(2\pi)^D i} \frac{ 4\left\{ g_{\mu\nu}m_r^2+(k_\mu p_\nu+k_\nu p_\mu)+2p_\mu p_\nu -g_{\mu\nu}p^2-g_{\mu\nu}k\cdot p \right\} }{(m_r^2-(k+p)^2)(m_r^2-p^2)} $$

あとは他のダイアグラムと同じように計算すればよいです：

\begin{align} \Pi^{ab}_{F\mu\nu}(k) &=-N_f {\rm tr}(T^aT^b) g_r^2\int_0^1 \int\frac{d^D \tilde p}{(2\pi)^D i} \frac{ 4\left\{ g_{\mu\nu} \left[ m_r^2+x(1-x)k^2+(2/D-1)\tilde p^2 \right] -2x(1-x)k_\mu k_\nu \right\}}{(-\tilde p^2+M)^2}\\ &= -N_f {\rm tr}(T^aT^b)g_r^2 \int_0^1 dx (4\pi)^{\epsilon-2}(-M)^\epsilon \Gamma(\epsilon)\\ &\times \left\{ -4i(g_{\mu\nu}(m_r^2+x(1-x)k^2)-2x(1-x)k_\mu k_\nu) +4g_{\mu\nu}(\frac{1}{2-\epsilon}-1)(-\frac{1}{2}(4-2\epsilon)M) (-\frac{1}{1-\epsilon}) \right\}\\ &=-8g_r^2N_f\delta_{ab}T_R (4\pi)^{\epsilon-2}\Gamma(\epsilon)(k^2g_{\mu\nu}-k_\mu k_\nu) \int_0^1dx \ x(1-x)M^{-\epsilon} \end{align}

ここで
$$ M=m_r^2-xk^2(1-x), \ \ \tilde p = p+kx, \ \ T_R=1/2 $$
です。

以上より

Counter term

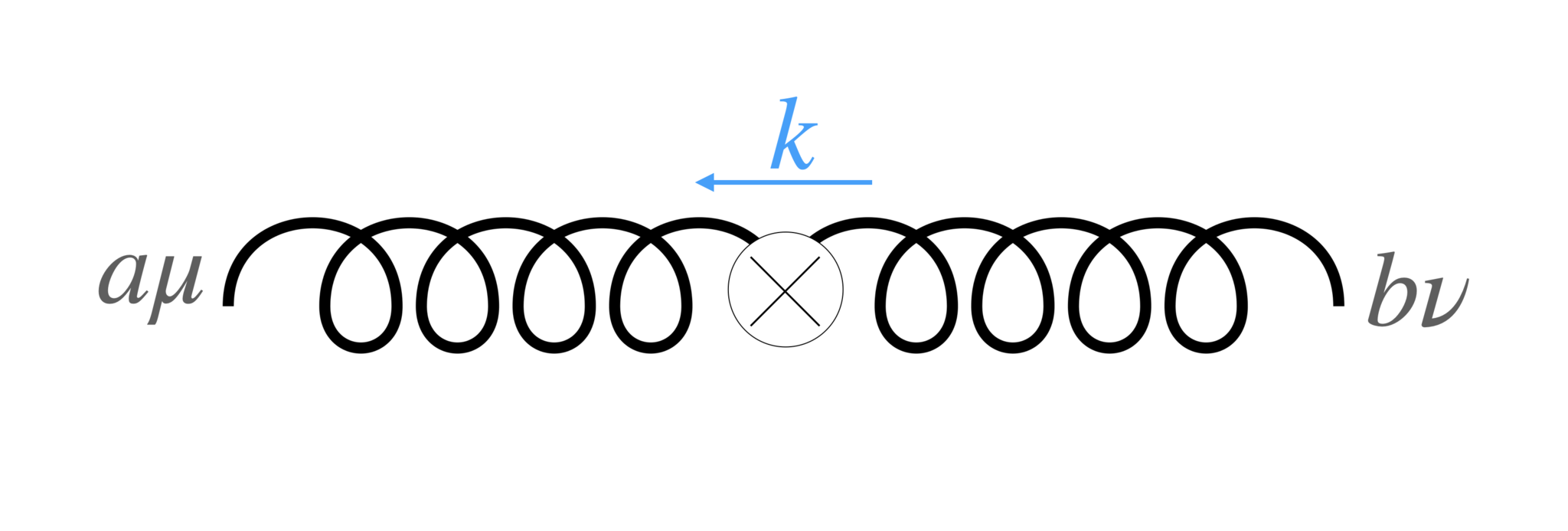counter term

Counter termは以下:

$Z_3$の決定

図２の寄与を全て足し合わせると、以下のようになります：
\begin{align} &\Pi^{ab}_{{\rm Gh}\mu\nu}+\Pi^{ab}_{T\mu\nu}+\Pi^{ab}_{{\rm G}\mu\nu} +\Pi^{ab}_{{F}\mu\nu}+\Pi^{ab}_{{\rm C}\mu\nu} \\ =& \ \ \ \ \ g_r^2\delta_{ab}C_G\frac{1}{3-2\epsilon} \left( \frac{1}{2}k^2g_{\mu\nu}+(1-\epsilon)k_\mu k_\nu \right) P(k^2,\epsilon) \\ &+0 \\ &+\frac{g_r^2}{2}C_G\delta_{ab} \frac{P(k^2,\epsilon)}{3-2\epsilon} \left[ g_{\mu\nu}k^2 \left\{ (19-12\epsilon) +2(1-4\epsilon)(3-2\epsilon)(1-\alpha_r) +\epsilon(3-2\epsilon)(1-\alpha_r)^2 \right\} \right. \\ &\left. \hspace{4.5cm} +k_\mu k_\nu \left\{ -2(11-7\epsilon) -2(1-4\epsilon)(3-2\epsilon)(1-\alpha_r)-(3-2\epsilon)\epsilon(1-\alpha_r)^2 \right\} \right] \\ & -8g_r^2N_f\delta_{ab}T_R (4\pi)^{\epsilon-2}\Gamma(\epsilon)(k^2g_{\mu\nu}-k_\mu k_\nu) \int_0^1dx \ x(1-x)M^{-\epsilon} \\ & +(Z_3-1)\delta_{ab}(k_\mu k_\nu -k^2g_{\mu\nu}) \end{align}

ただし$M=m^2-xk^2(1-x)$であり、$x$に依存していることに注意。まとめると
\begin{align} \frac{g_r^2}{2}C_G\delta_{ab} \frac{P(k^2,\epsilon)}{3-2\epsilon} ( g_{\mu\nu}k^2 -k_\mu k_\nu) \left\{ (20-12\epsilon) +2(1-4\epsilon)(3-2\epsilon)(1-\alpha_r) +\epsilon(3-2\epsilon)(1-\alpha_r)^2 \right\} \\-8g^2N_f\delta_{ab}T_R (4\pi)^{\epsilon-2}\Gamma(\epsilon)(k^2g_{\mu\nu}-k_\mu k_\nu) \int_0^1dx \ x(1-x)M^{-\epsilon} +(Z_3-1)\delta_{ab}(k_\mu k_\nu -k^2g_{\mu\nu}) \end{align}

となります。

次にこの結果を$\epsilon$でLaurent展開します。ところで、 前回の記事 に書いたように、次元正則化では$g$は質量次元$\epsilon$を持ちます。そこで、$\epsilon$で展開したのち、$g_r$を次元なしの結合定数$g_R$: $g_R=g_r\epsilon^{-\epsilon}$で書き直すことにします。書き直しは単純で、$g_r$を$g_R$にすればよいです。なぜなら、以降の計算に現れる最も強い発散項は$1/\epsilon$であり、このオーダーでは$g_R=g_r \mu^{-\epsilon}\simeq g_r(1-\ln(\mu)\epsilon+\cdots)$の${\cal O}(\epsilon)$の項は効かないからです$^{(**)}$。同時に$\epsilon$での展開ののち、$\alpha_r\rightarrow \alpha_R \ \ (\alpha_R=\alpha_r)$とします。

上記表式を$\epsilon$で展開し、$1/\epsilon$の項を拾うと（および$g_r\rightarrow g_R, \ \alpha_r\rightarrow \alpha_R$とする）

\begin{align} \frac{g_R^2}{(4\pi)^2}\delta_{ab}(k^2g_{\mu\nu}-k_\mu k_\nu) \left\{ -\frac{4}{3}N_f T_R+\frac{1}{2}C_G\left(\frac{13}{3}-\alpha_R\right) \right\}\frac{1}{\epsilon}+ (Z_3-1)\delta_{ab}(k_\mu k_\nu -k^2g_{\mu\nu}) \end{align}
になります。これがゼロになるように$Z_3$を決めると（minimal subtraction (MS) scheme）

を得ます。

$\tilde Z_3$の評価: ghostの2点1PI頂点関数のくりこみ定数の計算

$g^2$のオーダーにおけるghost 2点1PI頂点関数のダイアグラム

次に図8のghostの2点1PI頂点関数を計算します。これは簡単です。

Ghost self energy

ghost self energy

Feynman則より図9のghost self energy${\tilde \Pi}^{ab}$の寄与は以下のように書けます：
\begin{align} \tilde \Pi^{ab}(k)&=\int \frac{d^D q}{(2\pi)^D i} \frac{-1}{(k+q)^2}k^\mu (-ig_r f^{cad})(-ig_r f^{cdb})(k+q)^\nu \frac{d_{\mu\nu}(q^2)}{q^2}\\ &= g_r^2f^{cad}f^{cdb} \int \frac{d^D q}{(2\pi)^D i} \frac{1}{q^2(k+q)^2} \left(k\cdot(k+q) -(1-\alpha_r)\left(\frac{(k\cdot q)^2}{q^2}+(k\cdot q)\right)\right) \end{align}
公式15における$M$で書き直せば
\begin{align} =g_r^2f^{cad}f^{cdb} \left\{ k^2 M(1,1;1) -(1-\alpha_r)k^\mu k^\nu M(2,1;q_\mu q_\nu) +\alpha_r k^\mu M(1,1;q_\mu) \right\} \end{align}
となります。

公式15を使い

を得ます。

Counter term

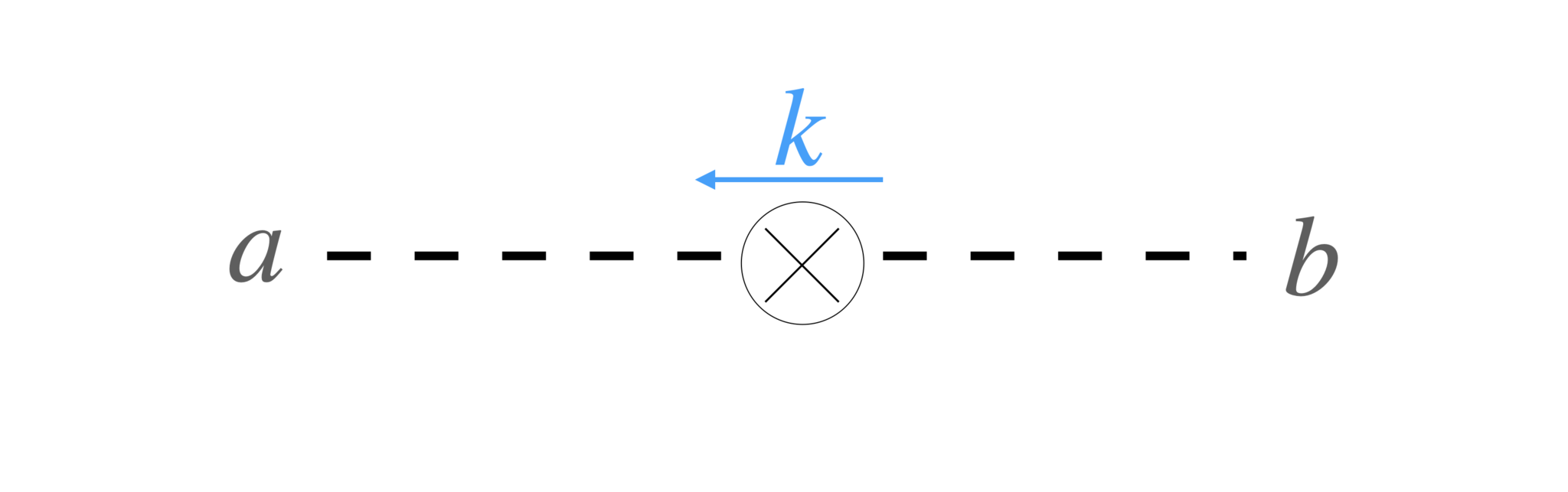counter term

図10のcounter termは以下：

$\tilde Z_3$の決定

$\epsilon$で展開し、$1/\epsilon$の部分を抜き出せば、$\tilde \Pi^{ab}(k)+$counter termは
\begin{align} -\frac{1}{2}\frac{g_R^2}{(4\pi)^2}C_G \frac{1}{\epsilon}\left(1+\frac{1-\alpha_R}{2}\right)\delta_{ab}k^2 + (\tilde Z_3-1)\delta_{ab}k^2 \end{align}
となります。ゆえにMS schemeで$\tilde Z_3$を決定すれば

となります。

$\tilde Z_1$の評価: ghost-ghost-gluon3点1PI頂点関数のくりこみ定数の計算

$g^2$のオーダーにおけるghost-ghost-gluon 3点1PI頂点関数のダイアグラム

最後に図11のghost-ghost-gluon 3点1PI頂点関数を計算します。

1つめのダイアグラム

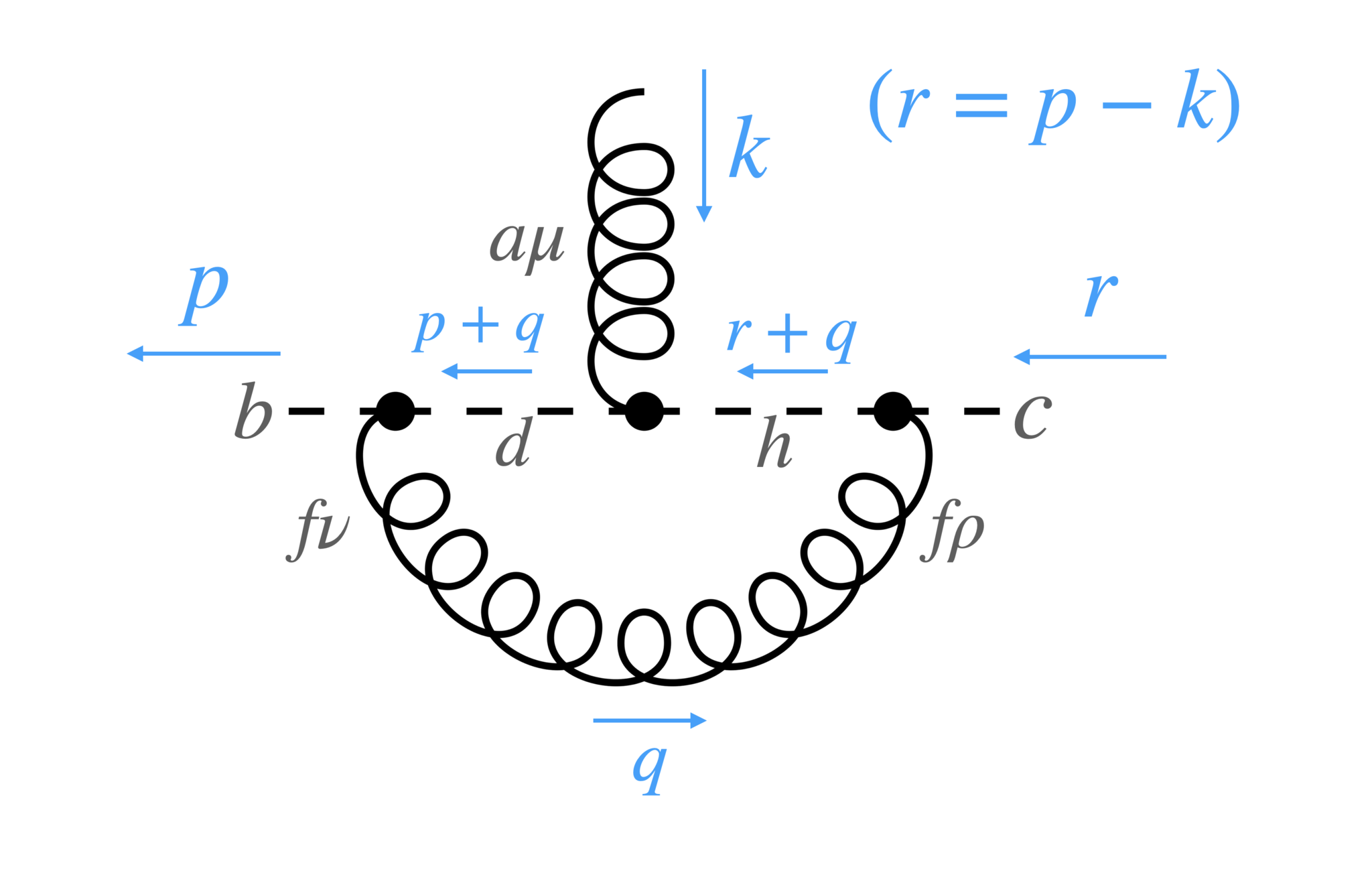1つめのダイアグラム。propagatorの両端のゲージ群のindexはデルタ関数により一致することを考慮している

図12のダイアグラム$\tilde \Lambda^{abc}_{1\mu}$は以下の式になります：
\begin{align} \tilde\Lambda^{abc}_{1\mu}(k,p,r)= (-ig_r)^3 f^{fbd}f^{fhc}f^{adh} \int\frac{d^Dq}{(2\pi)^Di}\frac{1}{(p+q)^2}\frac{d_{\nu\rho}(q)}{q^2} \frac{1}{(r+q)^2}p^\nu(r+q)^\rho(p+q)_\mu \end{align}
ゲージ群のファクターを計算し、整理すれば
\begin{align} =-ig_r^3\frac{C_G}{2}f^{abc} \int\frac{d^Dq}{(2\pi)^Di} \frac{(p\cdot(r+q))(p+q)_\mu-(1-\alpha_r)(q\cdot p)(q\cdot r/q^2+1)(p+q)_\mu}{q^2 (p+q)^2(q+r)^2}\tag{2} \end{align}
となります。

ここでは${\tilde \Lambda}^{abc}_{1\mu}$の発散する部分のみ計算します。
$\tilde\Lambda^{abc}_{1\mu}(k,p,r)$を計算するのに必要な積分は以下：
\begin{align} \bullet \displaystyle \int \frac{d^Dq}{(2\pi)^Di}\frac{1}{q^2(p+q)^2(q+r)^2}\\ \bullet \displaystyle \int \frac{d^Dq}{(2\pi)^Di}\frac{q_\mu}{q^2(p+q)^2(q+r)^2}\\ ★ \displaystyle \int \frac{d^Dq}{(2\pi)^Di}\frac{q_\mu q_\nu}{q^2(p+q)^2(q+r)^2}\\ \bullet \displaystyle \int \frac{d^Dq}{(2\pi)^Di}\frac{q_\mu q_\nu}{q^4(p+q)^2(q+r)^2}\\ \bullet \displaystyle \int \frac{d^Dq}{(2\pi)^Di}\frac{q_\mu q_\nu q_\rho}{q^4(p+q)^2(q+r)^2} \end{align}
このうち$D=4$において$q$が大きいとき発散するのは★のみ（$q$が大きいとき被積分関数は$\sim 1/q^4$。ほかは$1/q^5$またはそれより早く0になる）。よって発散項のみ計算するなら★を評価するだけでよいです。
（Appendixには上記5つの積分の計算結果を示しておきます）

分母をまとめたのち、公式12を用いて計算すると
\begin{align} \int \frac{d^Dq}{(2\pi)^Di}\frac{q_\mu q_\nu}{q^2(p+q)^2(q+r)^2} &=-\int_0^1dx\int_0^1dy \frac{y}{(4\pi)^{D/2}} \left[ \Gamma(3-D/2)P_\mu P_\nu L^{D/2-3} -\frac{1}{2}g_{\mu\nu}\Gamma(2-D/2)L^{D/2-2} \right]\\ &L:=(pxy-py+ry-r)^2+p^2xy-p^2y+r^2y-r^2 \end{align}
このうち$D\rightarrow 4$で発散するのは右辺第２項のみなので、これを抜き出します：
\begin{align} \to \frac{1}{2}\frac{g_{\mu\nu}}{(4\pi)^{D/2}}\Gamma(2-D/2)\int_0^1dxdy \ y \ L^{D/2-2}=\frac{1}{2}\frac{g_{\mu\nu}}{(4\pi)^{2-\epsilon}}\Gamma(\epsilon)\int_0^1 dx dy \ y \ L^{-\epsilon} \end{align}
ここでは発散項、つまり$1/\epsilon$に比例する項のみ評価したいので、$\Gamma(\epsilon)= 1/\epsilon+{\cal O}(\epsilon^0)$とし、他の部分の$\epsilon$はゼロにして
\begin{align} \frac{g_{\mu\nu}}{4}\frac{1}{(4\pi)^2}\frac{1}{\epsilon}+{\cal O}(\epsilon^0) \end{align}
を得ます。
Eq.(2)における★の係数は$-ig_r^3\frac{C_G}{2}f^{abc}\alpha_r p^\nu$なので、最終的に

となります。ここで$\cdots|_{\rm div}$は$\cdots$の発散部（divergent part）を表します。

2つめのダイアグラム

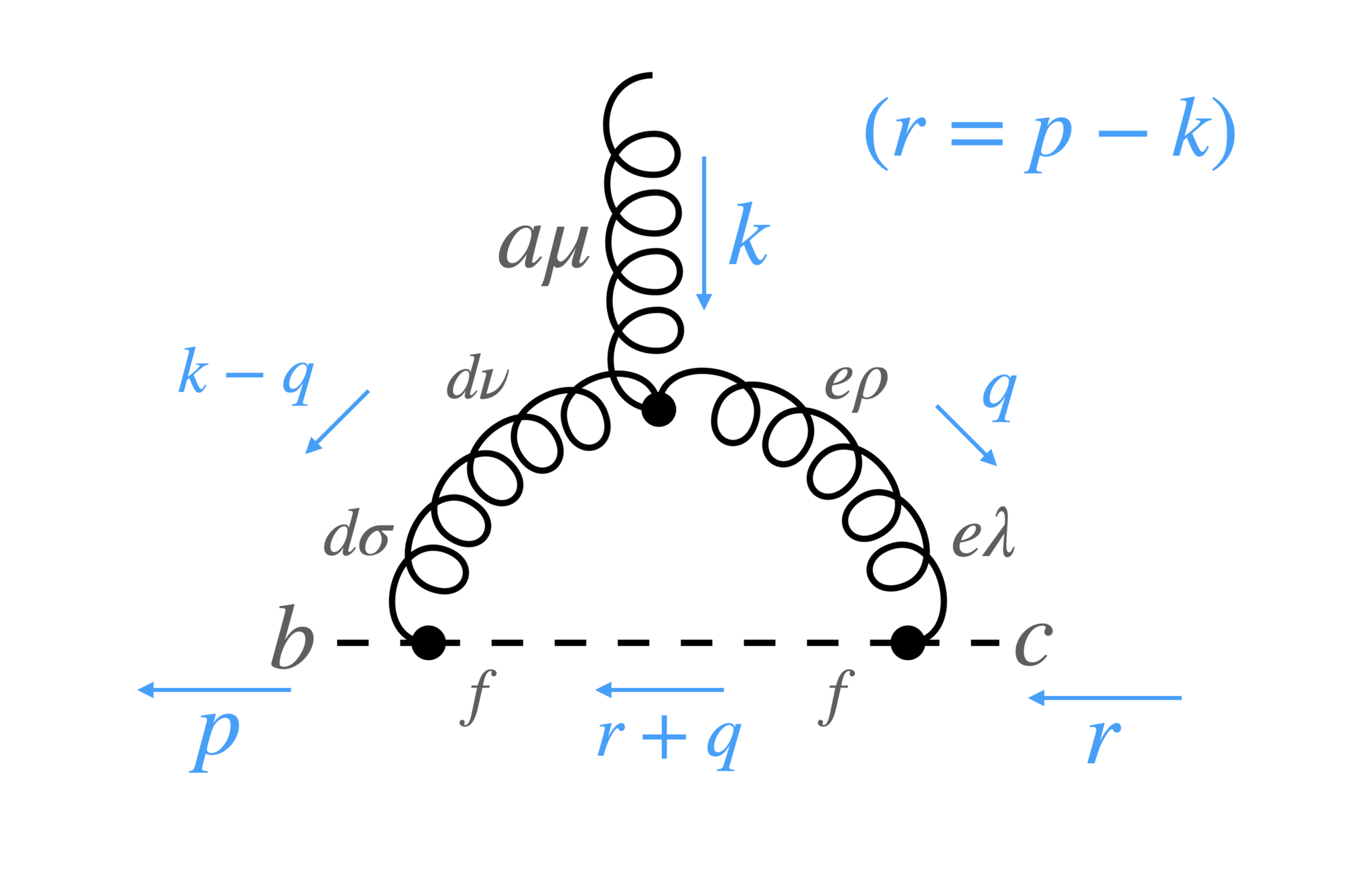2つめのダイアグラム。図12と同様、propagatorの両端のゲージ群のindexは一致させている

図13のダイアグラムはFeynman則より以下のようになります：
\begin{align} \tilde \Lambda^{abc}_{2\mu}(k,p,r) = -ig_r^3f^{bfd}f^{cef}f^{ade} \int \frac{d^D q}{(2\pi)^Di} \frac{ P_\sigma(r+q)_\lambda V_{\mu\nu\rho}(k,q-k,-q) d^{\sigma\nu}(k-q) d^{\lambda\rho}(q)} {(r+q)^2(k-q)^2 q^2} \end{align}

このダイアグラムも発散部のみ計算することにします。
次の記号を定義します：
\begin{align} L(a,b,c;x):= \int\frac{d^Dq}{(2\pi)^Di} \frac{x}{q^a(k-q)^b(r+q)^c} \end{align}
この記号を使って上記積分を書きなおすと、以下のようになります：
\begin{align} &\tilde \Lambda^{abc}_{2\mu}(k,p,r)=-ig_r^3f^{bfd}f^{cef}f^{ade}\\ \times \Big\{ &L[2,2,1;-(1-\alpha_r)^2(q\cdot r)(p\cdot(k-q))(q_\nu(k^2g^{\mu\nu}-k^\mu k^\nu)]\\ +&L[1,2,1; (1-\alpha_r)(p\cdot(k-q)) \left\{ -k^\mu (\alpha_r(k\cdot q)+k\cdot r)+q^\mu(\alpha_r k^2+q\cdot r)+k^2r^\mu \right\}]\\ +&L[1,1,1;-k^\mu (p\cdot(\alpha_r q+r))+q^\mu (p\cdot(-\alpha_r k+\alpha_r q+2r)) +p^\mu(2\alpha_r(k\cdot q)+2(k\cdot r)-\alpha_r(q\cdot r)) -r^\mu(p\cdot(k+q))]\\ +&L[2,1,1;(1-\alpha_r)(q\cdot r)\{-2p^\mu(k\cdot q)+q^\mu(p\cdot (k-q))+k^\mu(p\cdot q)\}]\\ +&L[0,2,1;-(1-\alpha_r)r^\mu p\cdot (k-q)]\\ +&L[0,1,1; -\alpha_r p^\mu]\Big\} \end{align}
これを計算するには、以下の積分が求まればよいです：
\begin{align} &L(2,2,1;q_\mu), L(2,2,1;q_\mu q_\nu), L(2,2,1;q_\mu q_\nu q_\rho),\\ &L(1,2,1;1), L(1,2,1;q_\mu), L(1,2,1;q_\mu q_\nu), L(1,2,1;q_\mu q_\nu q_\rho)\\ &L(1,1,1;1),L(1,1,1;q_\mu),L(1,1,1; q_\mu q_\nu),\\ &L(2,1,1;q_\mu q_\nu), L(2,1,1;q_\mu q_\nu q_\rho),\\ &L(0,2,1;1),L(0,2,1;q_\mu),\\ &L(0,1,1;1) \end{align}

発散項は、分母の$q$の次数から分子の$q$の次数を引いて4以下の項です。それは$L(1,1,1;q_\mu q_\nu)$と$L(0,1,1;1)$です。これらの項を取り出し、分母をまとめてから公式12を使うと以下のようになります（Appendixには上記15コ全ての積分の計算結果を示しておきます）:
\begin{align} &\left.\tilde \Lambda^{abc}_{2\mu}(k,p,r)\right|_{\rm div}\\ &= \left. -ig_r^3f^{bfd}f^{cef}f^{ade} \int\frac{d^Dq}{(2\pi)^Di} \left\{ \frac{-\alpha_r p^\mu}{(q-k)^2(q+r)^2} +\frac{\alpha_r p_\nu q^\mu q^\nu}{q^2(q-k)^2(q+r)^2} \right\}\right|_{\rm div} \\ &= \left. -ig_r^3f^{bfd}f^{cef}f^{ade}\left\{ -\alpha_r p^\mu\times\frac{\Gamma(\epsilon)}{(4\pi)^{2-\epsilon}} \int_0^1dxL_{011}^{-\epsilon} +\alpha_r p_\nu\times \frac{1}{2(4\pi)^{2-\epsilon}}g^{\mu\nu}\Gamma(\epsilon) \int_0^1 dx dy \ y \ L_{111}^{-\epsilon} \right\}\right|_{\rm div}\\ &= -ig_R^3f^{bfd}f^{cef}f^{ade} \left( -\alpha_R p^\mu \frac{1}{(4\pi)^2}\frac{1}{\epsilon} +\alpha_R p^\mu \frac{1}{4(4\pi)^2}\frac{1}{\epsilon} \right)\\ &= i\alpha_R g_R^3f^{bfd}f^{cef}f^{ade} p^\mu \frac{1}{(4\pi)^2} \frac{3}{4}\frac{1}{\epsilon}\\ &=-ig_Rf^{abc}p_\mu\frac{g_R^2}{(4\pi)^2}C_G\frac{3\alpha_R}{8\epsilon} \end{align}

よって

を得ます。

counter term

counter term

counter termは以下

$\tilde Z_1$の決定

以上より、図11のダイアグラムの発散部分は以下のように評価できます：
\begin{align} &{\tilde \Lambda^{abc}_{1\mu}}+{\tilde \Lambda^{abc}_{2\mu}}+\text{counter term}\\ &=-ig_Rf^{abc}p_\mu \frac{C_G}{2} \frac{g_R^2}{4}\frac{\alpha_R}{(4\pi)^2}\frac{1}{\epsilon}\\ &-ig_Rf^{abc}p_\mu\frac{g_R^2}{(4\pi)^2}C_G\frac{3\alpha_R}{8\epsilon}\\ &+(\tilde Z_1-1)(-ig_R)f^{abc}p_\mu \end{align}

MS schemeで$\tilde Z_1$を決定すると

$Z_g$の計算

以上で$\tilde Z_3, Z_3, \tilde Z_1$の計算が終わりました。Eq.($\color{blue}\boldsymbol{Z_3}$)、($\color{blue}\boldsymbol{\tilde Z_3}$)、($\color{blue}\boldsymbol{\tilde Z_1}$)より、
$$ Z_g={\tilde Z_1}/({\tilde Z_3} Z_3^{1/2}) $$
を$g_R^2$のオーダーで計算すると
\begin{align} Z_g &= \left( 1-\frac{g_R^2}{(4\pi)^2}C_G\frac{\alpha_R}{2\epsilon} \right) \left( 1+\frac{1}{2}\frac{g_R^2}{(4\pi)^2}C_G \left( 1+\frac{1-\alpha_R}{2} \right)\frac{1}{\epsilon} \right)^{-1} \left( 1+\frac{g_R^2}{(4\pi)^2} \left\{ -\frac{4}{3}N_F T_R+\frac{1}{2}C_G \left(\frac{13}{3}-\alpha_R \right) \right\} \frac{1}{\epsilon} \right)^{-1/2} +{\cal O}(g_R^4,\epsilon^0) \\ &=1-\frac{g_R^2}{(4\pi)^2} \frac{1}{\epsilon} \frac{1}{6}(11C_G-4T_R N_f) +{\cal O}(g_R^4,\epsilon^0) \end{align}
となります。

まとめ

今回は結合定数に関するくりこみ定数$Z_g$を
$$ Z_g={\tilde Z}_1/({\tilde Z}_3 Z_3^{1/2}) $$
$Z_3$: gluonの2点1PI頂点関数のくりこみ定数
$\tilde Z_3$: ghostの2点1PI頂点関数のくりこみ定数
$\tilde Z_1$: ghost-ghost-gluon3点1PI頂点関数のくりこみ定数

により計算しました。

結果をまとめると以下のようになります:

次回はこの$Z_g$を用いて、走る結合定数$g_R(\mu)$の計算を行います。

おしまい。${}_\blacksquare$

$\clubsuit$次の記事： 走る結合定数の計算(5/5): 結合定数のrunningの決定・漸近的自由性

$(*)$ flavorとは、u,d,s,c,b,tという6つのquarkの種類を指します。ただし$N_f$は必ずしも6を使うのではなく、理論や実験のエネルギースケールに応じて数を変化させます。それぞれの粒子の質量はeVを単位にして
u: 2-3MeV, d: 4-5MeV, s: 100MeV, c: 1.3GeV, b:4GeV, t: 173GeV
程度です。結合定数を測るエネルギースケールより重いquarkは基本的に無視します。走る結合定数（running coupling constant）に関しては Particle Daga Group (PDG)のQCDに関する記述 に詳しいです。
$(**)$ 実は、MS schemeでは、任意の$g_R$のオーダーにおいてくりこみ定数は顕わな$\mu$依存性を持ちません。$g_R$を通してのみ$\mu$に依存します（例えばRef.[1]P188参照のこと）。

Appendix

Feynman則

以下に本記事で用いたFeynman則を記しておきます。Ref.[1]のFeynman則を採用しています。青字がダイアグラムに対応する式です。

1. Propagator
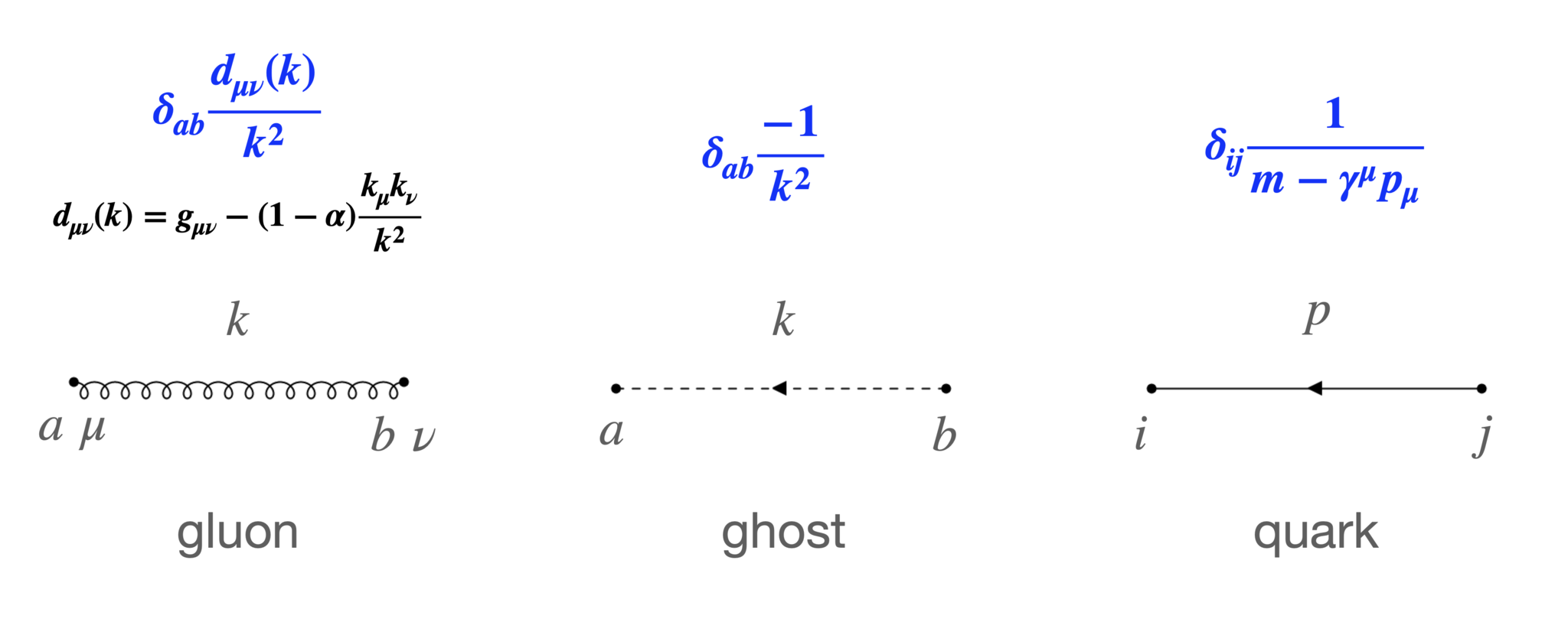   PropagatorのFeynman則

2. Vertex。運動量保存則を各vertexに課すことに注意。
   
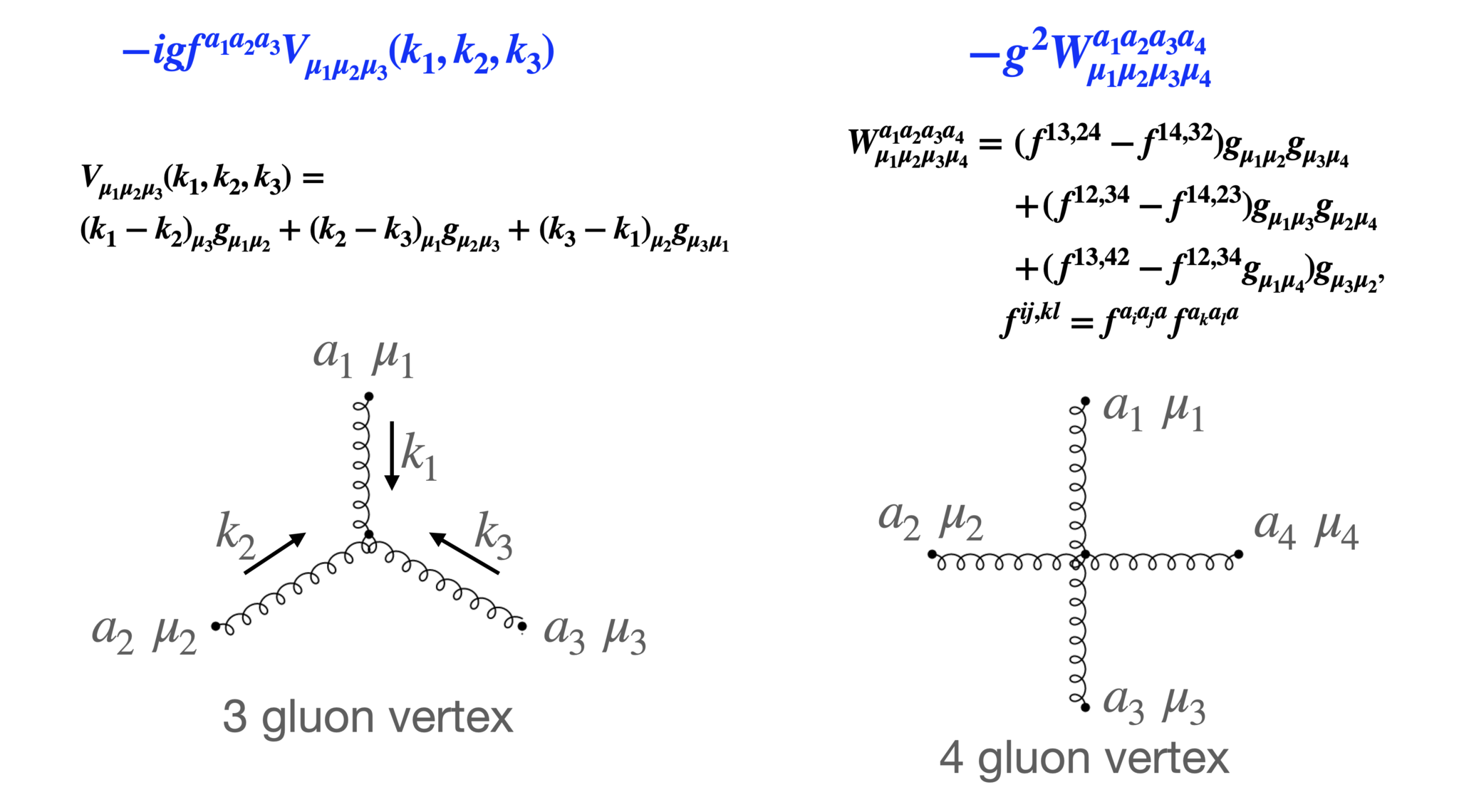
   VertexのFeynman則。上図がgluon、下図がghost-gluonおよびquark-gluon vertex。各vertexで運動量保存則を課す

3. ループ積分
   
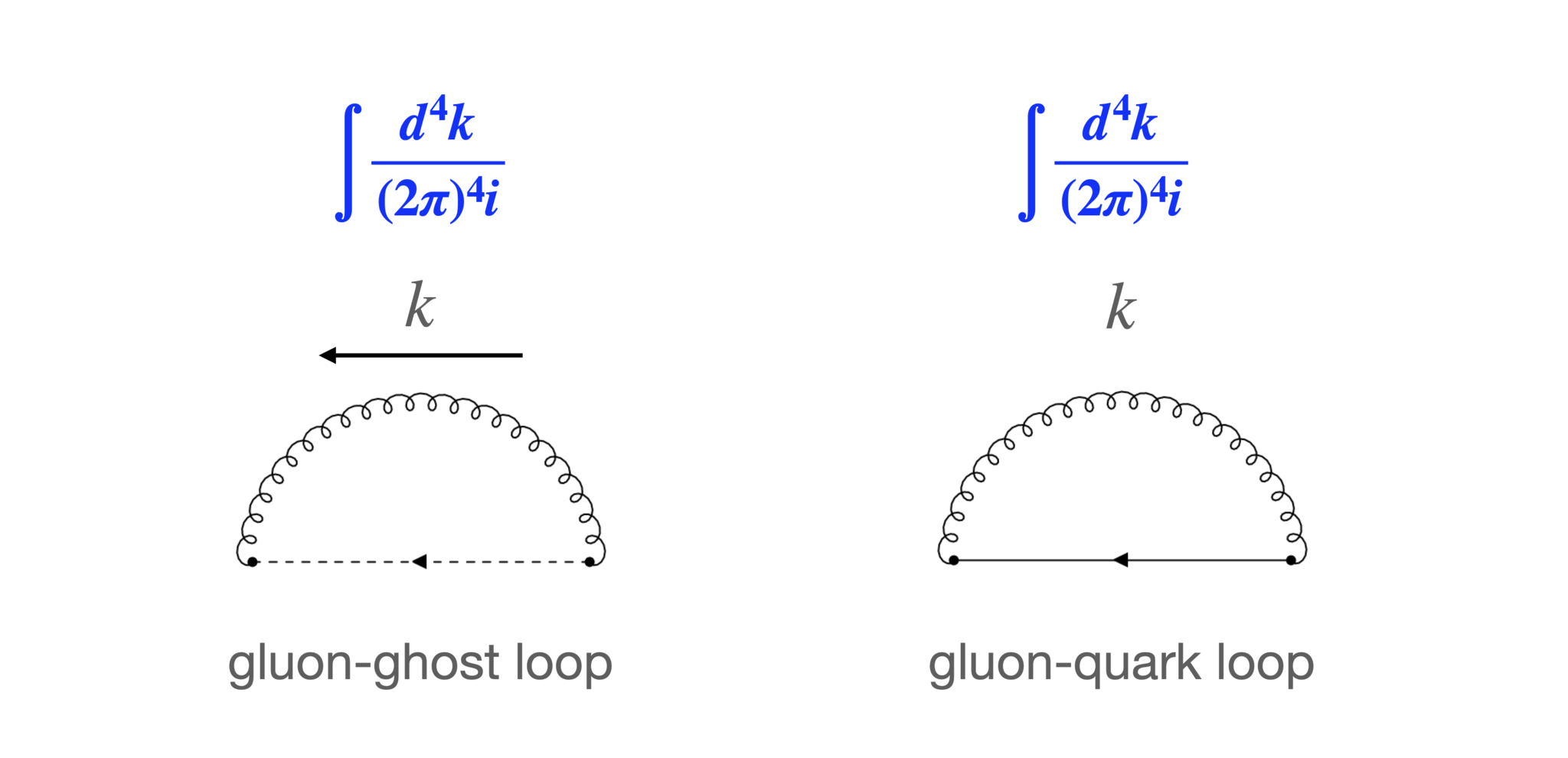   ループ積分因子

4. Counter terms
   
   Counter term

5. 対称因子
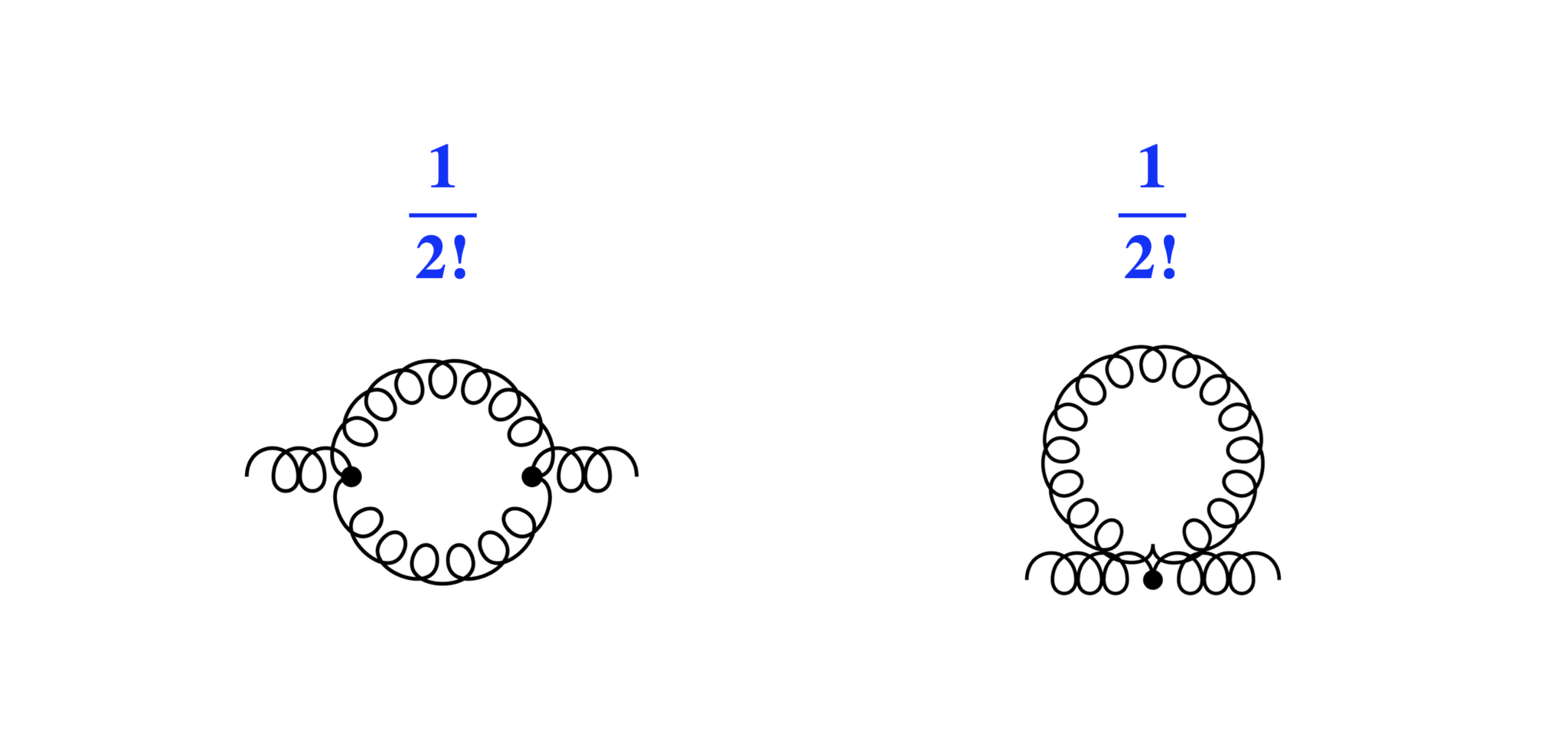   対称因子。上記2つのダイアグラム以外にこの因子は現れない。

$\tilde \Lambda_1$の計算に現れる積分

本文では発散項に必要な積分のみ計算しました。
ここでは、$\tilde \Lambda_1$の計算に現れるすべての積分を評価しておきます：

$\tilde \Lambda_2$の計算に現れる積分

$\tilde \Lambda_2$の計算に現れる積分は以下です。$\displaystyle L(a,b,c;x):=\int\frac{d^Dq}{(2\pi)^Di}\frac{x}{(q^2)^a\{(k-q)^2\}^b\{(q+r)^2\}^c}$とします。