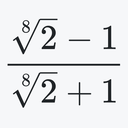q-ガウスの連分数
$$
\frac{\hygeo2\phi1{aq,b}{cq}{q,z}}
{(1-c)\hygeo2\phi1{a,b}{c}{q,z}}
=
\large{\mathop{\rm{K}}_{n=0}^\infty \frac{t_n}{1-cq^n}}
$$
\begin{eqnarray}
\lr\{{
\begin{array}{l}
t_0&=&1 \\
t_{2n-1}&=&q^{n-1}(cq^{n-1}-a)(1-bq^{n-1})z \\
t_{2n}&=&q^{n-1}(cq^{n}-b)(1-aq^{n})z
\end{array}
}.
\end{eqnarray}
q-超幾何関数
の比が連分数で表わされるというものであり、
ガウスの連分数
のq-類似に相当する。
次の補題2を用いて、ガウスの連分数と同様の処理をすることで導く。
$\displaystyle \hygeo2\phi1{a,b}{c}{q,z} - \hygeo2\phi1{aq,b}{cq}{q,z} = \frac{(c-a)(1-b)z}{(1-c)(1-cq)}\hygeo2\phi1{aq,bq}{cq^2}{q,z} $
\begin{eqnarray} (左辺) &=& \sum_{n=0}^\infty \lr({ \frac{(a,b;q)_n}{(c,q;q)_n} - \frac{(aq,b;q)_n}{(cq,q;q)_n} })z^n \\ &=& \sum_{n=0}^\infty \frac{(aq;q)_{n-1}(b;q)_n}{(c;q)_{n+1}(q;q)_n}\{(1-a)(1-cq^n)-(1-c)(1-aq^n)\}z^n \\ &=& (c-a)\sum_{n=0}^\infty \frac{(aq;q)_{n-1}(b;q)_n}{(c;q)_{n+1}(q;q)_n}(1-q^n)z^n \\ &=& (c-a)\sum_{n=1}^\infty \frac{(aq;q)_{n-1}(b;q)_n}{(c;q)_{n+1}(q;q)_{n-1}}z^n \\ &=& \frac{(c-a)(1-b)z}{(1-c)(1-cq)}\sum_{n=0}^\infty \frac{(aq,bq;q)_n}{(cq^2,q;q)_n}z^n \\ &=& \frac{(c-a)(1-b)z}{(1-c)(1-cq)}\hygeo2\phi1{aq,bq}{cq^2}{q,z} \\ &=& (右辺) \end{eqnarray}
$\displaystyle \frac{(-x,-y;q)_\infty-(x,y;q)_\infty}{(-x,-y;q)_\infty+(x,y;q)_\infty} = \large{\frac{x+y}{1-q+\mathop{\rm{K}}_{n=1}^\infty\frac{q^{n-1}(x+q^ny)(y+q^nx)}{1-q^{2n+1}}}} $
\begin{eqnarray} (左辺) &=& \large{ \frac{ \frac{1}{2} \left( \frac{(-x;q)_\infty}{(y;q)_\infty} - \frac{(x;q)_\infty}{(-y;q)_\infty} \right) } { \frac{1}{2} \left( \frac{(-x;q)_\infty}{(y;q)_\infty} + \frac{(x;q)_\infty}{(-y;q)_\infty} \right) } } \\ &=& \large{ \frac{ \sum_{n=0}^\infty \frac{(-\frac{x}{y};q)_{2n+1}}{(q;q)_{2n+1}}y^{2n+1} } { \sum_{n=0}^\infty \frac{(-\frac{x}{y};q)_{2n}}{(q;q)_{2n}}y^{2n} } \quad (\because q-二項定理) } \\ &=& { \frac{ \frac{1+\frac{x}{y}}{1-q}\hygeo2\phi1{-\frac{q^2x}{y},-\frac{qx}{y}}{q^3}{q^2,y^2} } { \hygeo2\phi1{-\frac{x}{y},-\frac{qx}{y}}{q}{q^2,y^2} } } \\ &=& \large{\frac{x+y}{1-q+\mathop{\rm{K}}_{n=1}^\infty\frac{q^{n-1}(x+q^ny)(y+q^nx)}{1-q^{2n+1}}}} \\ &=& (右辺) \end{eqnarray}
次回
は、今回の定理を用いて次式を示す。
$$
\begin{eqnarray}
\frac{\sqrt[8]{2}-1}{\sqrt[8]{2}+1}
&=&
\large{\mathop{\rm{K}}_{n=0}^\infty\frac{1}{2\sinh((2n+1)\pi)}}
\\ &=&
\cfrac{1}{
2\sinh\pi+\cfrac{1}{
2\sinh(3\pi)+\cfrac{1}{
2\sinh(5\pi)+\ddots}}}
\end{eqnarray}
$$
\begin{eqnarray}
\frac{\sqrt[4]{2}-1}{\sqrt[4]{2}+1}
&=&
\large{\mathop{\rm{K}}_{n=0}^\infty\frac{\cosh^2(n\pi)}{\sinh{((2n+1)\pi)}}}
\\ &=&
\cfrac{1}{
\sinh{\pi}+\cfrac{\cosh^2\pi}{
\sinh{(3\pi)}+\cfrac{\cosh^2(2\pi)}{
\sinh{(5\pi)+\ddots}}}}
\end{eqnarray}