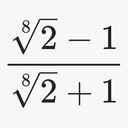双曲線関数を含む連分数
前回
示した定理3を用いて次式を示す。
$\beginend{eqnarray}{
\frac{\sqrt[8]{2}-1}{\sqrt[8]{2}+1}
&=&
{\Kfrac_{n=0}^\infty\frac{1}{2\sinh((2n+1)\pi)}}
}$
$\beginend{eqnarray}{
\frac{\sqrt[4]{2}-1}{\sqrt[4]{2}+1}
&=&
{\Kfrac_{n=0}^\infty\frac{\cosh^2(n\pi)}{\sinh{((2n+1)\pi)}}}
}$
前回の定理3より
$\beginend{align}{ { \frac {(-qz;q^2)_\infty - (qz;q^2)_\infty} {(-qz;q^2)_\infty + (qz;q^2)_\infty} } &= { \Kfrac_{n=0}^\infty\frac{1}{\frac{q^{-2n-1}-q^{2n+1}}{z}} } &&\normalsize\qquad(1.1.) \\ { \frac {(-qz;q^2)_\infty^2 - (qz;q^2)_\infty^2} {(-qz;q^2)_\infty^2 + (qz;q^2)_\infty^2} } &= \frac1{2} { \Kfrac_{n=0}^\infty\frac{{(q^{-n}+q^n)^2}}{\frac{q^{-2n-1}-q^{2n+1}}{z}} } &&\normalsize\qquad(1.2.) }$
$\displaystyle f(\tau) \coloneqq \prod_{n=0}^\infty \tanh\frac{-(2n+1)\pi i \tau}{2}$
これは、 モジュラーラムダ関数 と以下のような関係となっている。
$\beginend{eqnarray}{ \lambda(\tau) &=& {f}^8 {\qty(-\frac1\tau)} \\ \lambda^*(x) &=& {f}^4 {\qty(\frac{i}{\sqrt{x}})} }$
$\beginend{eqnarray}{
\frac{\sqrt2 \eta(\frac\tau2) \eta^2(2\tau)}{\eta^3(\tau)} &=&
\sqrt2\frac
{\sqrt\frac{2i}\tau \eta(-\frac2\tau) {\qty({\sqrt\frac{i}{2\tau} \eta(-\frac1{2\tau})})}^2}
{\qty({\sqrt\frac{i}\tau \eta(-\frac1\tau)})^3} \\&=&
\frac
{\eta(-\frac2\tau) \eta^2(-\frac1{2\tau})}
{\eta^3(-\frac1\tau)} \\&=&
\frac
{r^4(q^4;q^4)_\infty (r(q;q)_\infty)^2}
{(r^2(q^2;q^2))^3}
\qquad(q=e^{-{\frac{\pi i}{\tau}}}, r=q^\frac1{24}) \\&=&
\frac
{(q^4;q^4)_\infty (q;q)_\infty^2}
{(q^2;q^2)^3} \\&=&
\frac
{\frac{(q^4;q^4)_\infty}{(q^2;q^2)_\infty}(q;q)_\infty}
{\frac{(q^2;q^2)_\infty}{(q;q)_\infty}(q^2;q^2)_\infty} \\&=&
\frac
{(-q^2;q^2)_\infty(q;q)_\infty}
{(-q;q)_\infty(q^2;q^2)_\infty} \\&=&
\frac{(q;q^2)_\infty}{(-q;q^2)_\infty} \\&=&
\prod_{n=0}^\infty \frac{1-q^{2n+1}}{1+q^{2n+1}} \\&=&
\prod_{n=0}^\infty
\frac
{1-e^{-{\frac{(2n+1)\pi i}{\tau}}}}
{1+e^{-{\frac{(2n+1)\pi i}{\tau}}}} \\&=&
{f} {\qty(-\frac1\tau)} \\
}$
$\beginend{eqnarray}{
\lambda(\tau) &=& {f}^8 {\qty(-\frac1\tau)} \\
\lambda^*(x) &=& {f}^4 {\qty(\frac{i}{\sqrt{x}})}
}$
定理1,2より、
$\beginend{align}{ \frac {1-\sqrt[4]{\lambda^*(x)}} {1+\sqrt[4]{\lambda^*(x)}} &= {\Kfrac_{n=0}^\infty\frac{1}{2\sinh\frac{(2n+1)\pi}{\sqrt{x}}}} &&\normalsize\qquad(\because 1.1.) \\ \frac {1-\sqrt{\lambda^*(x)}} {1+\sqrt{\lambda^*(x)}} &= {\Kfrac_{n=0}^\infty\frac{\cosh^2\!\frac{n\pi}{\sqrt{x}}}{\sinh\frac{(2n+1)\pi}{\sqrt{x}}}} &&\normalsize\qquad(\because 1.2.) }$
これに
$\lambda^*(x)$の特殊値
を代入すれば最初の式が求まる。
また、
$\beginend{align}{
q\frac{(q^8z^{-1},q^8z;q^8)_\infty}{(q^4z^{-1},q^4z;q^8)_\infty} &=
\frac1{q^{-1}-q+\kfrac_{n=1}^\infty \frac{q^{-2n}+q^{2n}-z^{-1}-z}{q^{-2n-1}-q^{2n+1}}} \\
\sqrt{\lambda^*(x)} &=
{\Kfrac_{n=0}^\infty\frac{\cosh^2\!\frac{n\pi\sqrt{x}}4}{\sinh\frac{(2n+1)\pi\sqrt{x}}4}} \\
\frac{\sqrt[4]{\lambda^*(x)}}{\sqrt2} &=
\frac12\Kfrac_{n=0}^\infty
\frac{2\cosh\frac{n\pi\sqrt x}4}
{2\sinh\frac{(2n+1)\pi\sqrt x}8} \\
\frac{\sqrt{\lambda^*(x)+1}-1}{\sqrt{\lambda^*(x)}} &=
{\Kfrac_{n=0}^\infty\frac{1}{2\cosh\frac{(2n+1)\pi\sqrt{x}}4}} \\
\tan\frac{\pi}{48} &=
{\Kfrac_{n=0}^\infty\frac{1}{2\cosh\frac{(2n+1)\pi\sqrt{3}}2}}\\
f^2 {\qty(\tau+\frac1{2})} &=
e^{-{i\arccos f^4(2\tau)}}
}$
などが成り立つ。