モジュラー群Λとモジュラーλ関数
はじめに
この記事では後の記事に向けて$\Lambda$-モジュラー関数というものの簡単な性質について解説していきます。
$\Lambda$-モジュラー関数
昔に書いた モジュラー形式の記事 の言葉を引用すると、モジュラー関数とは以下のように定義されるものを言うのでした。
$\dis SL(2,\Z)=\left\{\begin{pmatrix}a&b\\c&d\end{pmatrix}\Bigg|\;a,b,c,d\in\Z,\;ad-bc=1\right\}$
の元$\dis\g=\begin{pmatrix}a&b\\c&d\end{pmatrix}$と複素数$z$に対してモジュラー変換$\g z$を
$$\dis\g z=\frac{az+b}{cz+d}$$
と定める。このときモジュラー変換全体のなす群$\G=SL(2,\Z)$をモジュラー群という。
(行列とモジュラー変換を同一視していることに注意する。)
上半平面$\H=\{z\in\C\mid\Im(z)>0\}$上の関数$f$であって次の条件を満たすもののことをモジュラー関数という。
- $f$は$\H$上有理型である
- $f$は任意のモジュラー変換$\g z=\frac{az+b}{cz+d}$に対して等式
$\dis f\left(\frac{az+b}{cz+d}\right)=f(z)$
を満たす。 - $f$はカスプ$z=i\infty$においても有理型である。
これに類似して$\Lambda$-モジュラー関数というものは以下のように定義されます。
モジュラー群$\Gamma$の部分群$\Lambda$を
$$\Lambda=\left\{\begin{pmatrix}a&b\\c&d\end{pmatrix}\in\Gamma\;\Bigg|\;a,d:奇数,\;b,c:偶数\right\}$$
によって定め、$\Lambda$の作用に対して不変でコンパクトリーマン面
$$\ol{\L\backslash\H}=(\L\backslash\H)\cup\{-1,0,i\infty\}$$
上有理型(後述)な関数$f$を$\Lambda$-モジュラー関数という。
$\Lambda$の構造
おおよそ 昔の記事 と同じ手順で$\Lambda$の構造を調べていきます。
$\Lambda$は変換群として$2$つの行列
$\M1201,\M1021$
によって生成される。つまり
$\Lambda=\left\langle\M1201,\M1021\right\rangle$
が成り立つ。
行列
$\M abcd$
に対し$a$についての数学的帰納法で示す。モジュラー変換として
$\M{-1}00{-1}=\M1001$
が成り立つので符号についてはあまり気にしないこととする。
$a=1$のとき
$ad-bc=d-bc=1$より$d=1+bc$なので
$\M1bc{1+bc}=\M10c1\M1b01=\M1021^{c/2}\M1201^{b/2}$
と主張を得る。
$a\geq3$のとき
転置を考えることで$|b|\leq|c|$としてよい。このとき
$$2|b|\leq2\sqrt{|bc|}\leq2\sqrt{|ad|+1}<2\l(\sqrt{|ad|}+1\r)\leq a+|d|+2$$
より$2|b|\leq a+|d|$が成り立つことに注意する。
・$|d|< a$のとき
$$\M abcd=\M d{-b}{-c}a^{-1}$$
より帰納法の仮定が適用できる。
・$2|b|< a+|d|$のとき、$|d\pm2b|=2|b|-|d|$となるように符号をとれば
$$\M10{\pm2}1\M abcd=\M ab{c\pm2a}{d\pm2b}=\M{d\pm2b}{-(c\pm2a)}{-b}a^{-1}$$
となるので帰納法の仮定が適用できる。
・$a\leq|d|$かつ$2|b|=a+|d|$のとき
$2|b|=a+|d|\leq2\sqrt{|ad|+1}$に注意すると$|b|=|c|,\;|d|=a+2$つまり
$$\M abcd=\M a{a+1}{-(a+1)}{-(a+2)}=\M{a-2}{a-1}{-(a-1)}{-a}\M{-1}{-2}23$$
がわかるので帰納法の仮定が適用できる。
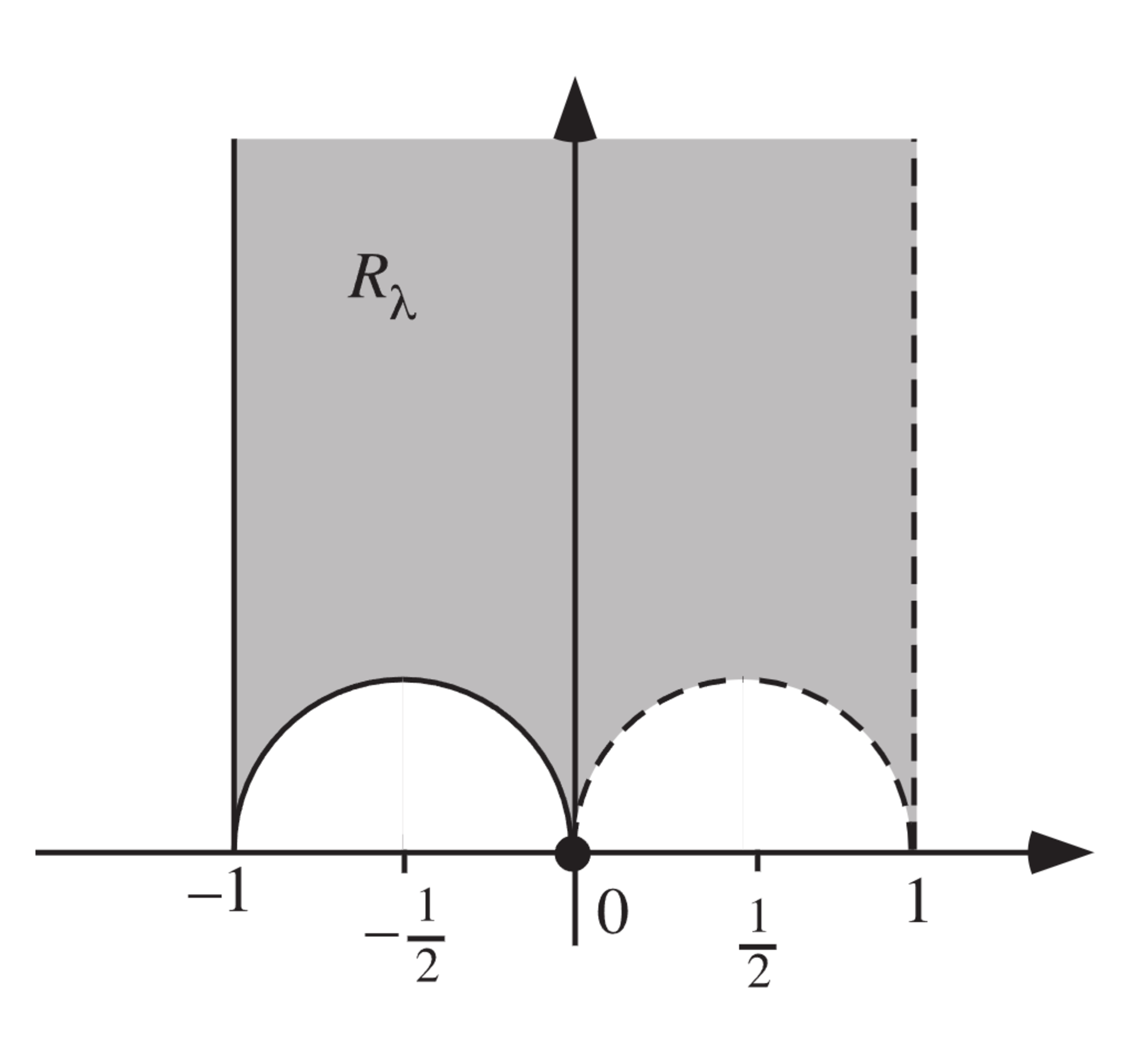
$\Lambda$の定める基本領域$\Lambda\backslash\H$は
$-1<\Re(z)<1$かつ$|2z+1|>1$かつ$|2z-1|>1$
を満たす領域とその境界線
$\Re(z)=-1$または$|2z+1|=1$
からなる。
 基本領域のイメージ図(Wolfram MathWorldより引用)
基本領域のイメージ図(Wolfram MathWorldより引用)
図の領域を$D$とおいたとき、
$(\mathrm{i})$任意の$z\in\H$に対してある$w\in D$と$\g\in\Lambda$があって$w=\g z$
$(\mathrm{ii})$任意の$z\in D,\;\g\in\Lambda$に対し$\g z\in D$ならば$\g z=z$
が成り立つことを示せばよい。
$(\mathrm{i})$の証明
$$\Im(\g z)=\Im\l(\frac{az+b}{cz+d}\r)$$
を最大にする、つまり$|cz+d|$を最小にするような$\g\in\Lambda$を取り
$$-1\leq\Re(\g z+2n)<1$$
となるような整数$n$に対し
$$\g'=\M1{2n}01\g,\quad w=\g'z=\g z+2n$$
とおく。
このとき$\Im(w)$の最大性から
$$\Im(\M10{\pm2}1w)=\Im\l(\frac{w}{1\pm2w}\r)=\farc{\Im(w)}{|1\pm2w|^2}\leq\Im(w)$$
つまり$|2w\pm1|\geq1$が成り立つので$w\in D$を得る。
($|2\g'z-1|=1$のときは$\g''=(\substack{1\;0\\-2\;1})\g',\;w=\g''z$とおけば$|2w+1|=1$となる。)
$(\mathrm{ii})$の証明
$z,\g z\in D$について$\Im(z)\leq\Im(\g z)$としてよい。このとき
$$\Im(z)\leq\frac{\Im(z)}{|cz+d|^2}$$
なので$z=x+iy$とおくと
\begin{eqnarray}
1&\geq&|cz+d|^2
\\&=&c^2(x^2+y^2)+2cdx+d^2
\\&\geq&c^2|x|+2cdx+d^2\qquad(\because|2z\pm1|^2-1=4(x^2\pm x+y^2)\geq0)
\\&\geq&(|c|-2|d|)|cx|+d^2
\\&\geq&\l\{\begin{array}{cl}d^2&(|c|\geq2|d|)\\(|c|-|d|)^2&(|c|<2|d|)\end{array}\r.\quad(\because|x|\leq1)
\end{eqnarray}
と評価できる。
- $|c|\geq2|d|$のとき
$1\geq d^2$より$|d|=1$となる。また$0=(|c|-2|d|)|cx|$となるので$|c|\geq2|d|>0$に注意すると$x=0$または$|c|=2|d|=2$が成り立つ。- $x=0$のとき
$1\geq|cz+d|^2=c^2y^2+1\geq4y^2+1>1$より矛盾。 - $|c|=2$のとき
$|2z\pm1|\leq1$より$|2z+1|=1$および$c=2d$でなければならない。このとき$c=2,d=1$としてよく、$ad-bc=a-2b=1$より$a=2b+1$となるが、$x^2+y^2=-x$に注意すると
$\dis\Re(\g z)=\Re\l(\frac{((2b+1)z+b)(2\ol z+1)}{|2z+1|^2}\r)=-2(2b+1)x+(4b+1)x+b=b-x$
なので$-1< x<0$より$-1\leq\Re(\g z)<1$であるためには$b=0$でなければならない。このとき
$\dis|2\g z-1|=\l|\frac{2z}{2z+1}-1\r|=\frac1{|2z+1|}=1$
となって矛盾。
- $x=0$のとき
- $|c|<2|d|$のとき
$1\geq(|c|-|d|)^2$より$(|c|-|d|)^2=1$が成り立つ。また
$(|c|-2|d|)|cx|+d^2=(|c|-|d|)^2$
となることから$x=-1$、
$1=|cz+d|^2=(cx+d)^2+c^2y^2\geq(c-d)^2$
となることから$(c-d)^2=1$が成り立ち、$c^2y^2=0$より$y>0$に注意すると$c=0,d=\pm1$が成り立つ。
しかし$ad-bc=\pm a=1$より$a=\pm1$がわかり、$\g z=z\pm b$となるので実部の範囲から$b=0$でなければならない。つまり$\g\equiv1$を得る。
基本領域についての注意点
上で挙げた基本領域$\L\backslash\H$は$\G\backslash\H$の場合と違って$i\infty$を付け加えただけではコンパクトリーマン面にはなりません。なぜなら$\Re(z)=0$を軸に折りたたんでリーマン面を作った時(
イメージ
)にその下端$z=0,\pm1$の点が欠けてしまうからです。したがって$\L$の基本領域がなすコンパクトリーマン面は$-1,0$も含めた領域$(\L\backslash\H)\cup\{-1,0,i\infty\}$を考えなければなりません。
また$\L$-モジュラー関数の定義では「$\ol{\L\backslash\H}$上有理型」という条件が出てきましたが、これは平たく言うと
・$\H$上有理型である。
・基本領域$\L\backslash\H$での$z\to-1,0,i\infty$における極限が存在する(あるいは$|f(z)|\to\infty$となる)。
と言い換えられます(多分)。ここらへんはリーマン面の理論によって精密に議論することができますが、とりあえずはこれくらいのお気持ちで大丈夫だと思います。
$\H$上有界な$\L$-モジュラー関数は定数関数に限る。
有界性より$f(0),f(-1),f(i\infty)$が存在するが、再び有界性より$h(z)=(f(z)-f(-1))(f(z)-f(0))(f(z)-f(i\infty))$は$\L\backslash\H$上、特に$\H$上でその絶対値を最大にするので最大値の原理よりそのような関数は定数関数でしかありえないことがわかる。
$\L\backslash\Q=\{-1,-\frac12,0\}$が成り立つ。
任意の有理数$p/q$に対して$qx-py=1$なる整数$x,y$を適当にとると、$p$が偶数のとき
$\dis\frac pq=\frac{0x+p}{0y+q}$
が、$q$が偶数のとき
$\dis\frac pq=\frac{-\frac12(2x-p)+x}{-\frac12(2y-q)+y}$
が、$p,q$が共に奇数のとき
$\dis\frac pq=\frac{-(x-p)+x}{-(y-q)+y}$
が成り立つので$\L\backslash\Q=\{-1,-\frac12,0\}$となることがわかる。
$p$次変換と$\Lambda$
奇素数$p$に対し
$$T_p=\l\{\l.\M abcd\r|ad-bc=p,\;a,d:奇数,\;b,c:偶数\r\}$$
と定め、その同値関係$A\sim_\L B\iff AB^{-1}\in\L$による商$\L\backslash T_p$を考えると
$$\L\backslash T_p=\l\{\L A_j\;\l|\;A_p=\M p001,\;A_j=\M1{2j}0p\quad(j=0,1,\ldots,p-1)\r.\r\}$$
が成り立つ。
$$\M1{2j}0p\M p001^{-1}=\frac1p\M1{2j}0p\M100p=\frac1p\M1{2pj}0{p^2}$$
$$\M1{2j}0p\M1{2j'}0p^{-1}=\frac1p\M1{2j}0p\M p{-2j'}01=\frac1p\M p{2(j-j')}0p$$
なので$2\nmid p$よりこれらは整数行列にならない。つまりこれらは異なる同値類を定めることがわかる。
いま任意の$A=\M abcd\in T_p$はある上三角行列と同値であることを示す。もし$A$が上三角行列ではない、つまり$c\neq0$であるとすると奇数性より$a\neq0$でもあることから$a=ga',c=gc'\;(g=\gcd(a,c))$に対し$a'x+c'y=1$となるような奇数$x$と偶数$y$が取れて、
$$\M xy{-c'}{a'}\M abcd=\M**0*$$
と$A$はある上三角行列と同値であることがわかる。いまこの行列式を考え、符号を適当にとることで
$$A\sim_\L\M p{2j}01,\M1{2j}0p$$
としてよい。また$j=qp+r$としたとき
$$\M1{-2j}01\M p{2j}01=\M p001$$
$$\M1{-2q}01\M 1{2j}0p=\M1{2r}0p$$
となることに注意すると主張を得る。
$\L$-モジュラー関数$f$に対し集合
$F(z)=\{f(A_jz)\mid 0\leq j\leq p\}$
は$\L$の作用$z\mapsto Az$に対して不変である。
特に$f(A_j z)$について対称的な関数は$\L$の作用に対して不変となる。
任意の$A\in\L$に対して$A_jA\in T_p$となるのである$k_j$があって$A_jA\sim_\L A_{k_j}$、つまり$f(A_jAz)=f(A_{k_j}z)$が成り立つ。またある$i\neq j$に対して$A_{k_i}\sim_\L A_{k_j}$が成り立つとすると$A_iA\sim_\L A_jA$つまり$A_i\sim_\L A_j$が成り立つことになり矛盾。よって
$F(Az)=\{f(A_{k_j}z)\mid 0\leq j\leq p\}=\{f(A_jz)\mid 0\leq j\leq p\}=F(z)$
を得る。
これらは$p$が一般の自然数であるときにも一般化できます。
自然数$p$に対し
$$T_p=\l\{\l.\M abcd\r|ad-bc=p,\;a:奇数,\;b,c:偶数\r\}$$
と定め、その同値関係$A\sim_\L B\iff AB^{-1}\in\L$による商$\L\backslash T_p$を考えると
$$\L\backslash T_p=\l\{\L A_{a,j}\;\l|\;A_{a,j}=\M a{2j}0d\quad(ad=p,\;0\leq j< d)\r.\r\}$$
が成り立つ。。また$\L$-モジュラー関数$f$に対して
$F(z)=\{f(Az)\mid A\in\L\backslash T_p\}$
とおくと、これは$\L$の作用に対して不変である。
またこれは$\G$についても成り立ちます。
正整数$p$に対し
$$S_p=\l\{\l.\M abcd\r|ad-bc=p\r\}$$
と定め、その同値関係$A\sim_\G B\iff AB^{-1}\in\G$による商$\G\backslash S_p$を考えると
$$\G\backslash S_p=\l\{\G B_{d,j}\;\l|\;B_{d,j}=\M dj0{p/d}\quad(d\mid p,\;j=0,1,\ldots,p/d-1)\r.\r\}$$
が成り立つ。またモジュラー関数$f$に対し
$F(z)=\{f(Bz)\mid B\in\G\backslash S_p\}$
とおくと、これは$\G$の作用に対して不変である。
モジュラー$\lambda$関数
代表的な$\L$-モジュラー関数としてモジュラー$\la$関数というものを紹介しておきます。
テータ関数$\t_j(\tau)=\t_j(0,\tau)$に対してモジュラー$\la$関数を
$$\la(\tau)=\frac{\t_2(\tau)^4}{\t_3(\tau)^4}$$
と定める。
これは 前回の記事 で定めた関数$k(\tau)$と$\la(\tau)=k(\tau)^2$という関係にあることがわかります。
関数$f$について任意の$\L$の作用$z\mapsto\frac{az+b}{cz+d}$に対して
$$f\l(\frac{az+b}{cz+d}\r)=(cz+d)^kf(z)$$
が成り立つことと
$\dis f(z+2)=f(z)$かつ$\dis f\l(\frac z{2z+1}\r)=(2z+1)^kf(z)$かつ$f(z)=(-1)^kf(z)$
が成り立つことは同値である。
命題1から 昔の記事 の命題3と同様にしてわかる。
$\t_2(\tau)^4,\t_3(\tau)^4,\t_4(\tau)^4$は重さ$2$の$\L$-モジュラー形式である。特に$\la(\tau)$は$\L$-モジュラー関数となる。
\begin{eqnarray}
\t_3(\tau+2)&=&\t_3(\tau)
\\\t_3(-1/\tau)&=&\sqrt{-i\tau}\t_3(\tau)
\end{eqnarray}
に注意すると
\begin{eqnarray}
\t_3\l(\frac\tau{2\tau+1}\r)^2
&=&i\l(2+\frac1\tau\r)\t_3\l(-2-\frac1\tau\r)^2
\\&=&i\l(2+\frac1\tau\r)\t_3\l(-\frac1\tau\r)^2
\\&=&i\l(2+\frac1\tau\r)\cdot(-i\tau)\t_3(\tau)^2
\\&=&(2\tau+1)\t_3(\tau)^2
\end{eqnarray}
が成り立つ。また同様に
\begin{eqnarray}
\t_2(\tau+2)&=&e^{\pi i/2}\t_2(\tau)
\\\t_4(\tau+2)&=&\t_4(\tau)
\\\t_2(-1/\tau)&=&\sqrt{-i\tau}\t_4(\tau)
\\\t_4(-1/\tau)&=&\sqrt{-i\tau}\t_2(\tau)
\end{eqnarray}
から
$$\t_2\l(\frac\tau{2\tau+1}\r)^2=(2\tau+1)\t_2(\tau)^2$$
$$\t_4\l(\frac\tau{2\tau+1}\r)^2=-(2\tau+1)\t_4(\tau)^2$$
がわかるので命題9より主張を得る。
$\la$は$\L$の作用に対して不変ですが、$\G$の作用に対してもある種の保型性が成り立ちます。
$$\la\l(\tau+1\r)=\frac{\la(\tau)}{\la(\tau)-1},\;\la\l(-\frac1\tau\r)=1-\la(\tau)$$
が成り立つ。特に$\la$は$\G$の作用$z\mapsto Az$に対して
$$\la,1-\la,\frac1\la,\frac1{1-\la},\frac\la{\la-1},1-\frac1\la$$
のいずれかに移る。
$\tau\mapsto\tau+1$において$q\mapsto-q$となるので
\begin{eqnarray}
\t_2(\tau+1)&=&\sum^\infty_{n=-\infty}(-1)^{n(n+1)}e^{\pi i/4}q^{(n+\frac12)^2}
=e^{\pi i/4}\sum^\infty_{n=-\infty}q^{(n+\frac12)^2}=e^{\pi i/4}\t_2(\tau)
\\\t_3(\tau+1)&=&\sum^\infty_{n=-\infty}(-q)^{n^2}
=\sum^\infty_{n=-\infty}(-1)^nq^{n^2}=\t_4(\tau)
\end{eqnarray}
が成り立つ。よってヤコビの恒等式$\t_2^4+\t_4^4=\t_3^4$とヤコビの変換公式に注意すると
\begin{eqnarray}
\la(\tau+1)&=&\frac{-\t_2(\tau)^4}{\t_4(\tau)^4}
=\farc{\t_2(\tau)^4}{\t_2(\tau)^4-\t_3(\tau)^4}=\frac{\la(\tau)}{\la(\tau)-1}
\\\la\l(-\frac1\tau\r)&=&\frac{\t_4(\tau)^4}{\t_3(\tau)^4}=1-\la(\tau)
\end{eqnarray}
を得る。
また$\G$は$\M1101,\M0{-1}10$によって生成されるので、その作用による$\la$の行き先は$\M101{-1},\M{-1}101$によって生成される。この生成元を$S,T$とおくと$S^2=T^2=(ST)^3=I$が成り立つことから
\begin{eqnarray}
\langle S,T\rangle&=&\{I,S,T,ST,TS,STS\}
\\&=&\l\{\M1001,\M101{-1},\M{-1}101,\M1{-1}10,\M01{-1}1,\M0110\r\}
\end{eqnarray}
つまり
$$\langle S,T\rangle\la
=\l\{\la,\frac{\la}{\la-1},1-\la,1-\frac1\la,\frac1{1-\la},\frac1\la\r\}$$
を得る。
テータ関数$\t_2(\tau),\t_3(\tau)$は$\H$において零点も極も取らず、$\tau=i\infty$つまり$q=0$においては$\t_2(i\infty)=0,\t_3(\tau)=(i\infty)=1$が成り立つので$\la(\tau)$は$\H\cup\{i\infty\}$上で正則となります。つまり命題3によって定数関数とならないためには$\la(\tau)$は$\Q$上で極を取る必要があります。
$\la(0)=1,\la(-\frac12)=0,\la(-1)=\infty$が成り立つ。
$\la(i\infty)=0$と
$$\la\l(-\frac1\tau\r)=1-\la(\tau)$$
から$\la(0)=1$、それに加えて
$$\la\l(\tau-1\r)=\frac{\la(\tau)}{\la(\tau)-1}$$
から$\la(-1)=\infty$、さらに
$$\la\l(\frac{\tau}{1-\tau}\r)=\frac1{\la(\tau)}$$
から$\la(-\frac12)=0$を得る。
またこの結果と命題4より$\la$の有理数点での挙動は以下のようになります。
$\dis\la\l(\frac pq\r)=\l\{\begin{array}{cl} 1&(p:偶数) \\0&(q:偶数) \\\infty&(p,q:奇数) \end{array}\r.$が成り立つ。
ちょっとした補題
最後に後の記事で使うことになる命題を一つ示しておきます。
ヤコビの楕円関数$\sn(u,k)$を
前回の記事
の定理11
$$\sn(u,k)=\sn[u,\tau]=\frac{\t_3(\tau)}{\t_2(\tau)}\frac{\t_1(v,\tau)}{\t_4(v,\tau)}
\quad\l(k=\frac{\t_2(\tau)^2}{\t_3(\tau)^2},\;v=\frac u{\pi\t_3(\tau)^2}\r)$$
によって$\tau$の関数とみなしたとき、$\sn[u,\tau]$は$\L$-モジュラー関数となる。
\begin{eqnarray}
\t_1(v,\tau+2)&=&e^{\pi i/2}\t_1(v,\tau+2)
\\\t_2(v,\tau+2)&=&e^{\pi i/2}\t_2(v,\tau+2)
\\\t_3(v,\tau+2)&=&\t_3(v,\tau+2)
\\\t_4(v,\tau+2)&=&\t_4(v,\tau+2)
\end{eqnarray}
およびヤコビの変換公式
\begin{eqnarray}
A(v,\tau)&=&\sqrt{-i\tau}e^{\pi iv^2/\tau}
\\\t_1\l(\frac v{\tau},-\frac1\tau\r)&=&-iA(v,\tau)\t_1(v,\tau)
\\\t_2\l(\frac v{\tau},-\frac1\tau\r)&=&A(v,\tau)\t_4(v,\tau)
\\\t_3\l(\frac v{\tau},-\frac1\tau\r)&=&A(v,\tau)\t_3(v,\tau)
\\\t_4\l(\frac v{\tau},-\frac1\tau\r)&=&A(v,\tau)\t_2(v,\tau)
\end{eqnarray}
に注意すると
\begin{eqnarray}
\sn[u,\tau+2]&=&\sn[u,\tau]
\\\sn\l[u,\frac\tau{2\tau+1}\r]
&=&\frac{\t_3(\frac\tau{2\tau+1})}{\t_2(\frac\tau{2\tau+1})}
\frac{\t_1(\frac v{2\tau+1},\frac\tau{2\tau+1})}{\t_4(\frac v{2\tau+1},\frac\tau{2\tau+1})}
\\&=&-i\frac{\t_3(-2-\frac1\tau)}{\t_4(-2-\frac1\tau)}
\frac{\t_1(-\frac v\tau,-2-\frac1\tau)}{\t_2(-\frac v\tau,-2-\frac1\tau)}
\\&=&(-i)^2\frac{\t_3(\tau)}{\t_2(\tau)}\frac{\t_1(-v,\tau)}{\t_2(-v,\tau)}
\\&=&-\sn[-u,\tau]=\sn[u,\tau]
\end{eqnarray}
がわかるので命題7より主張を得る。
この命題は$\tau$が異なっていても$k^2$の値が同じであれば$\sn(u,k)$も同じ関数を定めることを示しています。
