黄金比の連分数展開と区間縮小法の原理
Introduction
以前、 「区間縮小法の原理で『2乗して2になる正の実数（√2）』の存在を確認する」 という記事を書きました。
記事の内容としては
高校の教科書などで紹介されている「$\sqrt{2}$は無理数」の証明について、「そもそも2乗して2になる正の実数の存在が証明されていない」といった指摘を見かけます。
今回は「区間縮小法の原理」を使いながら、2乗して2になる正の実数の存在を確認していきます。
といったものです。中間値の定理ですぐに確認できてしまいますが、勉強をかねて区間縮小法の原理を使ってみました。区間を縮小させる方法としては、二分法（中点を次々に取り続けていく）を使っています。
この記事に対し、Twitterで「連分数展開を使った区間の縮小の仕方を採用することもできる」といった旨のコメントを見かけました。
そして、それを実際に行ったものを教えていただきました（ $\sqrt{2}$は実数 ）。
今回は、 このページ を参考にしつつ、$\sqrt{2}$ではなく、黄金比をテーマにして同じことを試してみたいと思います。
連分数展開のアイデア
天下り的ではありますが、
$\alpha^2-\alpha-1=0$
を満たすような$\alpha$が何かしら存在すると仮定します。
$0^2-0-1=-1$なので、$\alpha \not= 0$です。
このとき
$ \displaystyle{ \begin{align} \alpha^2 &= \alpha+1\\ \end{align} }$
なので、両辺を$\alpha(\not = 0)$で割ると
$\alpha = 1+\frac{1}{\alpha}$
となります。
実験
数列$\{a_n\}$を以下の漸化式で定めます。
$a_1 = 1$
$a_{n+1} = 1+\frac{1}{a_n}$
このときの$a_n$の値および${a_n}^2-a_n-1$の値を具体的に計算してみます。
※私は「浮動小数点とかなんもわからん」という人間なのですが、とりあえず「BigFloat」と書いてプログラミングしてみました。計算結果について「大体このくらいの値になるんだな」と大らかな目で見ていただければと思います（言語は Julia を使いました）。
$a_n$
n=1: 1.0
n=2: 2.0
n=3: 1.5
n=4: 1.666666666666666666666666666666666666666666666666666666666666666666666666666678
n=5: 1.599999999999999999999999999999999999999999999999999999999999999999999999999986
n=6: 1.625
n=7: 1.615384615384615384615384615384615384615384615384615384615384615384615384615386
n=8: 1.619047619047619047619047619047619047619047619047619047619047619047619047619048
n=9: 1.617647058823529411764705882352941176470588235294117647058823529411764705882352
n=10: 1.618181818181818181818181818181818181818181818181818181818181818181818181818172
${a_n}^2-a_n-1$
n=1: -1.0
n=2: 1.0
n=3: -0.25
n=4: 0.1111111111111111111111111111111111111111111111111111111111111111111111111111303
n=5: -0.04000000000000000000000000000000000000000000000000000000000000000000000000002211
n=6: 0.015625
n=7: -0.005917159763313609467455621301775147928994082840236686390532544378698224852074174
n=8: 0.00226757369614512471655328798185941043083900226757369614512471655328798185942739
n=9: -0.0008650519031141868512110726643598615916955017301038062283737024221453287197161908
n=10: 0.0003305785123966942148760330578512396694214876033057851239669421487603305784917384
見えてくること
- $a_n$は$1.618$くらいの値に近付いていきそう
- ${a_n}^2-a_n-1$は$0$に近付いていきそう
- ${a_n}^2-a_n-1$は偶数番号で$0$以上、奇数番号で$0$以下のようだ
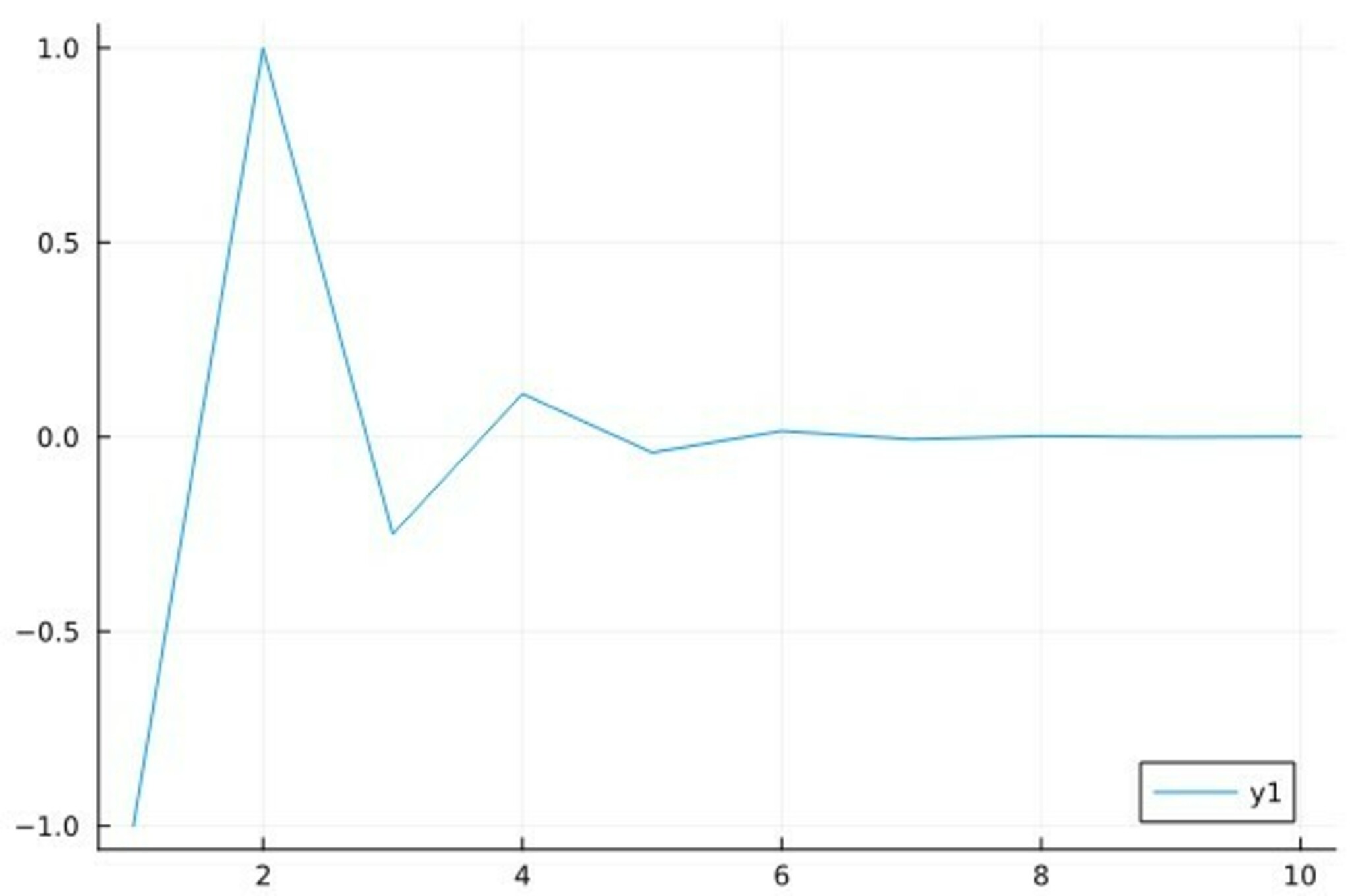x軸:n/y軸:(a_n)^2-a_n-1
※
Plots.jl
でグラフ描画
目標と方針
目標
ここまでの実験を踏まえて、以下の命題を証明していきます。
$u^2-u-1=0$を満たす$1$以上の実数$u$が存在する。
その際、以下（区間縮小法の原理）を使っていきます。
（実数の）閉区間の入れ子の列
$[a_1,b_1] \supseteq [a_2,b_2]\supseteq \cdots \supseteq [a_n,b_n] \supseteq \cdots$
において
$\lim_{n \to \infty}(b_n-a_n)=0$
が成立するならば、この区間列は（実数内に）ただ1つの共通要素をもつ。
（参考：藤田博司「『集合と位相』をなぜ学ぶのか」p.67）
方針
先と同様、数列$\{a_n\}$を
$a_1 = 1$
$a_{n+1} = 1+\frac{1}{a_n}$
と定めます。
さらに、$\{a_n\}$を奇数番号と偶数番号に分けて、新たな数列$\{b_n\},\{c_n\}$を以下のように定めます。
$b_n = a_{2n-1}$
$c_n = a_{2n}$
そして、$\lim_{n \to \infty}(c_n-b_n)=0$となることを示し、閉区間の入れ子の列
$[b_1,c_1] \supseteq [b_2,c_2]\supseteq \cdots \supseteq [b_n,c_n] \supseteq \cdots$
のただ1つの共通要素$u$が$u^2-u-1=0$を満たすことを確認していきます。
補題たち
数列$\{a_n\}$を以下で定める。
$a_1 = 1$
$a_{n+1} = 1+\frac{1}{a_n}$
$a,b$を$1$以上の実数とする。このとき
$a \leqq b \Longleftrightarrow a^2-a-1 \leqq b^2-b-1$
$(b^2-b-1)-(a^2-a-1) = (b-a)(b+a-1)$
となる。
（$\Longrightarrow$を示す）
$a \leqq b$ならば$b-a \geqq 0$である。また、$a,b$は$1$以上の実数であることから$b+a-1 > 0$なので、$a^2-a-1 \leqq b^2-b-1$が成り立つ。
（$\Longleftarrow$を示す）
$a^2-a-1 \leqq b^2-b-1$ならば$(b-a)(b+a-1) \geqq 0$となる。
$a,b$は$1$以上の実数なので、$b+a-1 > 0$である。
$(b-a)(b+a-1) \geqq 0$であることから、$b-a \geqq 0$となるので、$a \leqq b$が成り立つ。
$a_n \geqq 1$
数学的帰納法で示す。
$n=1$のとき、$a_1 = 1$より成り立つ。
$n=k$のとき$a_k \geqq 1$であると仮定する。
$\frac{1}{a_k} > 0$なので
$a_{k+1} = 1+ \frac{1}{a_k} \geqq 1$となり、$n=k+1$のときも成り立つ。
よって、任意の正の整数$n$に対して、$a_n \geqq 1$が成り立つ。
$n$が奇数ならば${a_n}^2-a_n-1 \leqq 0$
$n$が偶数ならば${a_n}^2-a_n-1 \geqq 0$
$ \displaystyle{ \begin{align} {a_{n+1}}^2-a_{n+1}-1 &= \Big(1+\frac{1}{a_n}\Big)^2-\Big(1+\frac{1}{a_n}\Big)-1\\ &= 1+\frac{2}{a_n}+\Big(\frac{1}{a_n} \Big)^2-\Big(1+\frac{1}{a_n}\Big)-1\\ &= -1 + \frac{1}{a_n} + \Big(\frac{1}{a_n} \Big)^2\\ &= \frac{-{a_n}^2+a_n+1}{{a_n}^2}\\ &= \frac{-({a_n}^2-a_n-1)}{{a_n}^2} \end{align} }$
となるので
${a_n}^2-a_n-1 \leqq 0$ならば${a_{n+1}}^2-a_{n+1}-1 \geqq 0$
${a_n}^2-a_n-1 \geqq 0$ならば${a_{n+1}}^2-a_{n+1}-1 \leqq 0$
であることがわかる。
$n=1$のとき、${a_1}^2-a_1-1=-1 \leqq 0$なので
$n$が奇数ならば${a_n}^2-a_n-1 \leqq 0$
$n$が偶数ならば${a_n}^2-a_n-1 \geqq 0$
が成り立つ。
数列$\{b_n\},\{c_n\}$を以下で定める。
$b_n = a_{2n-1}$
$c_n = a_{2n}$
補題3,4より
$b_n \geqq 1,\ c_n \geqq 1$
${b_n}^2-b_n-1 \leqq 0$
${c_n}^2-c_n-1 \geqq 0$
$b_n \leqq b_{n+1} \leqq c_{n+1} \leqq c_n$
$ \displaystyle{ \begin{align} c_n &= 1+\frac{1}{b_n}\\ &= \frac{b_n+1}{b_n} \end{align} }$
$ \displaystyle{ \begin{align} b_{n+1} &= 1+\frac{1}{c_n}\\ &= 1+\frac{b_n}{b_n+1}\\ &= \frac{2b_n+1}{b_n+1} \end{align} }$
$ \displaystyle{ \begin{align} c_{n+1} &= 1+\frac{1}{b_{n+1}}\\ &= 1+\frac{b_n+1}{2b_n+1}\\ &= \frac{3b_n+2}{2b_n+1} \end{align} }$
（$b_n$と$b_{n+1}$について）
$ \displaystyle{
\begin{align}
b_{n+1}-b_n &= \frac{2b_n+1}{b_n+1}-b_n\\
&= \frac{2b_n+1-b_n(b_n+1)}{b_n+1}\\
&= \frac{2b_n+1-{b_n}^2-b_n}{b_n+1}\\
&=\frac{-({b_n}^2-b_n-1)}{b_{n+1}}
\end{align}
}$
${b_n}^2-b_n-1 \leqq 0$なので$b_{n+1}-b_n \geqq 0$である。
よって$b_{n+1} \geqq b_n$となる。
（$b_{n+1}$と$c_{n+1}$について）
$ \displaystyle{
\begin{align}
c_{n+1}-b_{n+1} &= \frac{3b_n+2}{2b_n+1}-\frac{2b_n+1}{b_n+1}\\
&= \frac{(3b_n+2)(b_n+1)-(2b_n+1)^2}{(2b_n+1)(b_n+1)}\\
&= \frac{3{b_n}^2+5b_n+2-4{b_n}^2-4b_n-1}{(2b_n+1)(b_n+1)}\\
&= \frac{-{b_n}^2+b_n+1}{(2b_n+1)(b_n+1)}\\
&= \frac{-({b_n}^2-b_n-1)}{(2b_n+1)(b_n+1)}\\
\end{align}
}$
${b_n}^2-b_n-1 \leqq 0$なので$c_{n+1}-b_{n+1} \geqq 0$である。
よって$c_{n+1} \geqq b_{n+1}$となる。
（$c_n$と$c_{n+1}$について）
$ \displaystyle{
\begin{align}
c_{n}-c_{n+1} &= \frac{b_n+1}{b_n}-\frac{3b_n+2}{2b_n+1}\\
&= \frac{(b_n+1)(2b_n+1)-b_n(3b_n+2)}{b_n(2b_n+1)}\\
&= \frac{2{b_n}^2+3b_n+1-3{b_n}^2-2}{b_n(2b_n+1)}\\
&= \frac{-{b_n}^2+3b_n-1}{b_n(2b_n+1)}\\
&= \frac{-({b_n}^2-b_n-1)+2(b_n-1)}{b_n(2b_n+1)}\\
\end{align}
}$
${b_n}^2-b_n-1 \leqq 0$であり、$b_n \geqq 1$なので$c_{n}-c_{n+1} \geqq 0$である。
よって$c_{n} \geqq c_{n+1}$となる。
$c_{n+1}-b_{n+1} \leqq \frac{1}{3}(c_n-b_n)$
$ \displaystyle{ \begin{align} (2b_n+1)(b_n+1)-3b_n &= 2{b_n}^2+3b_n+1-3b_n\\ &= 2{b_n}^2+1 \geqq 0 \end{align} }$
よって$(2b_n+1)(b_n+1) \geqq 3b_n$となるので
$ \displaystyle{ \begin{align} \frac{1}{(2b_n+1)(b_n+1)} \leqq \frac{1}{3b_n} \end{align} }$
が成り立つ。
両辺に$-({b_n}^2-b_n-1)\ (\geqq 0)$をかけると
$ \displaystyle{ \begin{align} \frac{-({b_n}^2-b_n-1)}{(2b_n+1)(b_n+1)} \leqq \frac{-({b_n}^2-b_n-1)}{3b_n} \ \cdots (1) \end{align} }$
となる。
$ \displaystyle{ \begin{align} c_n-b_n &= \frac{b_n+1}{b_n}-b_n\\ &= \frac{b_n+1-{b_n}^2}{b_n}\\ &= \frac{-({b_n}^2-b_n-1)}{b_n} \ \cdots (2) \end{align} }$
であることと、補題5の証明から
$ \displaystyle{ \begin{align} c_{n+1}-b_{n+1} = \frac{-({b_n}^2-b_n-1)}{(2b_n+1)(b_n+1)} \ \cdots (3) \end{align} }$
なので、(2)(3)を(1)に代入すると
$c_{n+1}-b_{n+1} \leqq \frac{1}{3}(c_n-b_n)$
が成り立つことがわかる。
命題1の証明
＜命題1＞
$u^2-u-1=0$を満たす$1$以上の実数$u$が存在する。
補題6より
$c_{n}-b_{n} \leqq \Big(\frac{1}{3}\Big)^{n-1}(c_1-b_1)$
となるので、$b_1=1,c_1=2$より
$c_{n}-b_{n} \leqq \Big(\frac{1}{3}\Big)^{n-1}$
である。
よって
$\lim_{n \to \infty}(c_n-b_n)=0$
となるので、区間縮小法の原理より、閉区間の入れ子の列
$[b_1,c_1] \supseteq [b_2,c_2]\supseteq \cdots \supseteq [b_n,c_n] \supseteq \cdots$
は、（実数内）にただ1つの共通要素$u$を持つことがわかる。
任意の正の整数$n$に対して
$(1 \leqq )b_n \leqq u \leqq c_n$
なので、補題2から
${b_n}^2-b_n-1 \leqq u^2-u-1 \leqq {c_n}^2-c_n-1 \ \cdots(1)$
であることがわかる。
ここで、数列$\{d_n\},\{e_n\}$を以下で定める。
$d_n = {b_n}^2-b_n-1$
$e_n = {c_n}^2-c_n-1$
補題5より
$(1 \leqq ) b_n \leqq b_{n+1} \leqq c_{n+1} \leqq c_n$
であることと、補題2から
$d_n \leqq d_{n+1} \leqq e_{n+1} \leqq e_n$
が成り立つ。
また
$ \displaystyle{ \begin{align} e_n-d_n &= {c_n}^2-c_n-1 -({b_n}^2-b_n-1)\\ &= (c_n-b_n)(c_n+b_n-1) \end{align} }$
となる。
$c_{n}-b_{n} \leqq \Big(\frac{1}{3}\Big)^{n-1}$
であることと
$b_n \leqq c_n \leqq c_1 (=2)$
であることから
$e_n-d_n \leqq \Big(\frac{1}{3}\Big)^{n-1}(c_1+c_1-1)$
となるので
$ \displaystyle{ \begin{align} e_n-d_n \leqq \Big(\frac{1}{3} \Big)^{n-2} \end{align} }$
が成り立つ。
よって
$\lim_{n \to \infty}(e_n-d_n)=0$
となるので、区間縮小法の原理より、閉区間の入れ子の列
$[d_1,e_1] \supseteq [d_2,e_2]\supseteq \cdots \supseteq [d_n,e_n] \supseteq \cdots$
は、（実数内）にただ1つの共通要素$v$を持つことがわかる。
(1)より、任意の正の整数$n$に対して
$d_n \leqq u^2-u-1 \leqq e_n$
となることがわかるので、$u^2-u-1$は閉区間の入れ子の列
$[d_1,e_1] \supseteq [d_2,e_2]\supseteq \cdots \supseteq [d_n,e_n] \supseteq \cdots$
の共通要素である。
したがって、$v=u^2-u-1$である。
また、補題4より、任意の正の整数$n$に対して
$d_n \leqq 0 \leqq e_n$
となることがわかるので、$0$は閉区間の入れ子の列
$[d_1,e_1] \supseteq [d_2,e_2]\supseteq \cdots \supseteq [d_n,e_n] \supseteq \cdots$
の共通要素である。
したがって、$u^2-u-1=0$である。
補足
命題1の証明で
$\lim_{n \to \infty}\Big(\frac{1}{3}\Big)^{n}=0$
を使っていますが、これは数列$\{\frac{1}{3^n}\}$が$\{\frac{1}{n}\}$の部分列であることから、証明できます（$\{\frac{1}{n}\}$が$0$に収束することはアルキメデスの性質を使って示します）。
くわしくは 「1/2^nは0に収束する」を証明する（1/nの部分列であることを使いながら） を参照してみてください。
感想など
黄金比や$\sqrt{2}$だけでなく、もっと一般的に考えてみたくなりました。
今まで連分数にあまり触れたことがなかったんですが、面白いですね！
また、こういった類の話は「黄金比ありき」「$\sqrt{2}$ありき」で考えてしまいがちですが、天下り的なことをしつつも、「そもそも存在するのか？を示すんだ」というところを強く意識するのがポイントなのかな…と思います。この辺りが難しくもあり、面白いところだと感じます。
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
