反転共役という変換
はじめに
反転の派生の1つについて書きます．
補題 8.16 (重ね描きを強制的に作る反転)．
三角形$ABC$において，$A$を中心とする半径$\sqrt{AB \cdot AC}$の円に関して反転し，$\angle BAC$の二等分線に関して対称移動すると，$B$と$C$が入れかわる．
(参考文献[1]p.221 より引用)
はい．船旅に載っているやつです．名前がないと不便なので，以降，この方法を反転共役と呼称します．
Googleで検索しても，この名称を使っているサイトは1つ(参考文献[2])しか見つかりませんでしたが，「反転共役」というワードはかなり気に入っているので，これから浸透してくれると嬉しいです．浸透させましょう．
追記(2023/4/4):よく見ると「共役反転」でした．まあ可換なので…
定義など
(Mathlogの記事で反転共役をやるのはこれで$3$回目ですが，定義の仕方が全く統一されていないそうですね．)
定義
三角形$\triangle ABC$をとり，その外接円を$\Gamma$とします．
点$X$を中心$A$，半径$\sqrt{AB \cdot AC}$の円で反転し，$\angle BAC$の二等分線で鏡映して得られる点を$X^{\star}$と書くことにします．
また，反転共役による集合$\Sigma$の像$\{X^{\star}|X \in \Sigma\}$も，同じように${\Sigma}^{\star}$と書きます．
基本的な性質
どの補題も，かなり頻繁に使います．
$B^{\star}=C$,$C^{\star}=B$
最初に引用したやつですね．
直線$s$が$A$を通るとき，$s^{\star}$は$s$の等角共役線である．
反転共役の"共役"の要素です．
$\Gamma^{\star}$は直線$BC$である．
$\Gamma$は点$A$を通るので，$\Gamma^{\star}$は直線．
$\Gamma$は点$B,C$を通るので，$\Gamma^{\star}$は点$B^{\star}(=C),C^{\star}(=B)$を通る．
したがって，$\Gamma^{\star}$は直線$BC$である．
$X \neq A, Y \neq A$のとき，
- $X^{\star}Y^{\star}=\dfrac{AB \cdot AC}{AX \cdot AY} \cdot XY$
- $XY=\dfrac{AB \cdot AC}{AX^{\star} \cdot AY^{\star}} \cdot X^{\star}Y^{\star}$
分数の部分は対称性でうまく消えてくれる場合があります．
使用例
反転共役が刺さる例を$5$つ紹介します．
反転共役を扱った記事を既に$2$つ書いているので，まずはそれらを紹介します．
過去の記事
トレミーの定理
円$\Gamma$上の(凸)四角形$ABCD$について、
$$AB \cdot CD + BC \cdot DA = AC \cdot BD$$
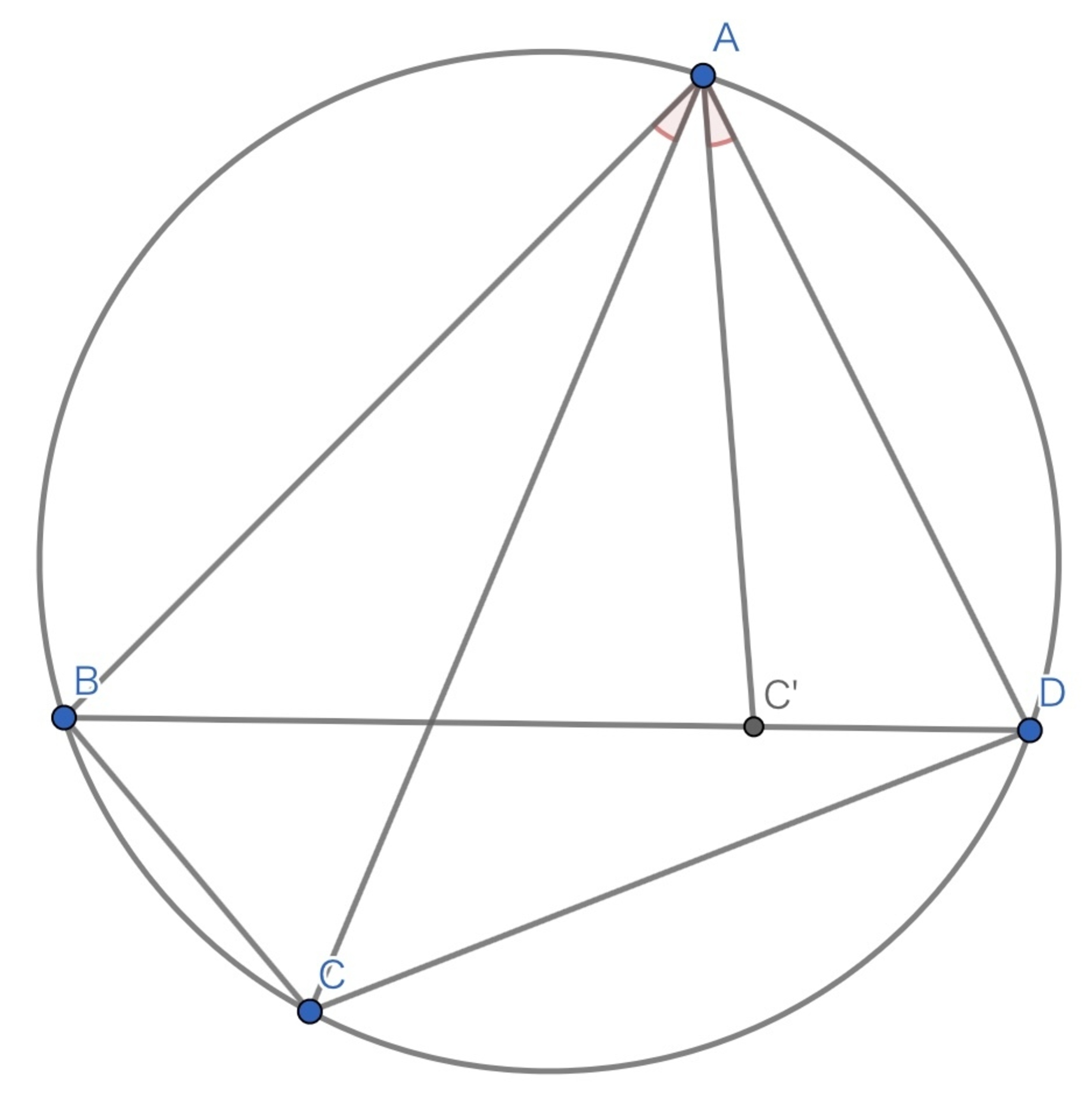トレミーの定理
どれかの頂点で反転共役すれば示せます．
詳しい証明は，
トレミーの定理の有名な証明で出てくる等角共役線が反転共役由来だと主張する記事
を参照してください．
混線内接円
辺$AB,AC$と円$\Gamma$に接する円を$\Omega _A$とおく．(この円は「$\triangle ABC$の($\angle A$内の)混線内接円」と呼ばれるものである)
このとき，${\Omega _A}^{\star}$は$\triangle ABC$の$A$-傍接円である．
$\Gamma^{\star}$は直線$BC$であるから，${\Omega _A}^{\star}$は直線$AC,AB,BC$に接する円である．
$\Omega _A$は$\angle BAC$の内側に位置し，反転と鏡映でこれは変わらない．
$\Omega _A$は$\Gamma$に関して無限遠点の逆側に存在するから，${\Omega _A}^{\star}$は直線$BC$に関して点$A$の逆側に存在する．
したがって，${\Omega _A}^{\star}$は$\triangle ABC$の$\angle A$内の傍接円．
混線内接円は，円に接する円として定義されているので，(狭義の)初等幾何で扱いにくそうですが，反転共役をすると格段にやりやすくなることがわかります．
実際にどんなことをできるかは，
混線内接円の記事
に詳しく書いています．
等角共役線
反転共役により，点$A$を通る直線は，その等角共役線にうつるのでした．(補題2)
この性質，等角共役線に刺さると思いませんか？
刺さると思うので検証します！
直線$BC$上に点$P$を任意にとる．直線$AP$の等角共役線と直線$BC$の交点を$Q$とおく．
このとき，$\dfrac{BP}{PC} \cdot \dfrac{BQ}{QC} = \left( \dfrac{AB}{AC} \right) ^2$
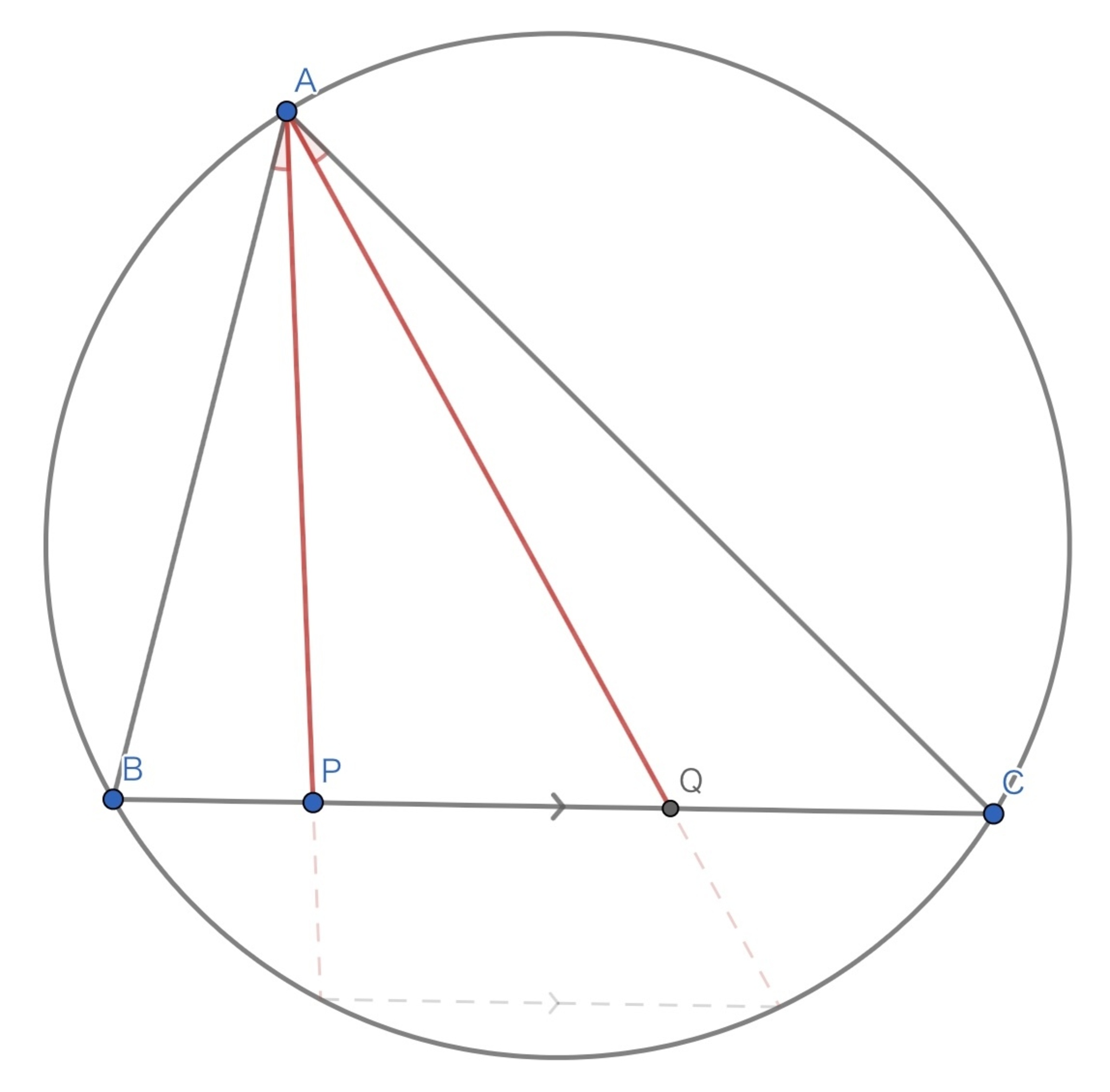等角共役線
直線$AP,BC$の交点$P$の反転共役$P^{\star}$は，直線$AQ$と円$\Gamma$の交点である．
直線$AQ,BC$の交点$Q$の反転共役$Q^{\star}$は，直線$AP$と円$\Gamma$の交点である．
距離の変換公式より，
$$\begin{aligned}
\dfrac{BP}{PC} \cdot \dfrac{BQ}{QC}
&= \left( \dfrac{AP^{\star} \cdot AC^{\star}}{AB^{\star} \cdot AP^{\star}}\cdot \dfrac{B^{\star}P^{\star}}{P^{\star}C^{\star}} \right) \cdot
\left( \dfrac{AQ^{\star} \cdot AC^{\star}}{AB^{\star} \cdot AQ^{\star}}\cdot \dfrac{B^{\star}Q^{\star}}{Q^{\star}C^{\star}} \right) \\
&= \dfrac{AB}{AC} \cdot \dfrac{CP^{\star}}{P^{\star}B} \cdot \dfrac{AB}{AC} \cdot \dfrac{CQ^{\star}}{Q^{\star}B} \\
\end{aligned}$$
ここで，$\measuredangle BCQ^{\star} = \measuredangle BAQ^{\star} = \measuredangle P^{\star}AC = \measuredangle P^{\star}Q^{\star}C$ より，四角形$BCP^{\star}Q^{\star}$は台形で，共円性より特に等脚台形であるから，$CP^{\star} = Q^{\star}B, CQ^{\star} = P^{\star}B$
したがって，$\dfrac{BP}{PC} \cdot \dfrac{BQ}{QC} = \dfrac{AB}{AC} \cdot \dfrac{AB}{AC}$である．
等角共役線(反転共役後)
刺さりました．勝ちです！(?)
別の例も見てみましょう．
角の二等分線
定理7で，$P = Q$としてみます．
$\angle BAC$の二等分線と直線$BC$の交点を$D$とおくと，
$$\dfrac{BD}{DC} = \dfrac{AB}{AC}$$
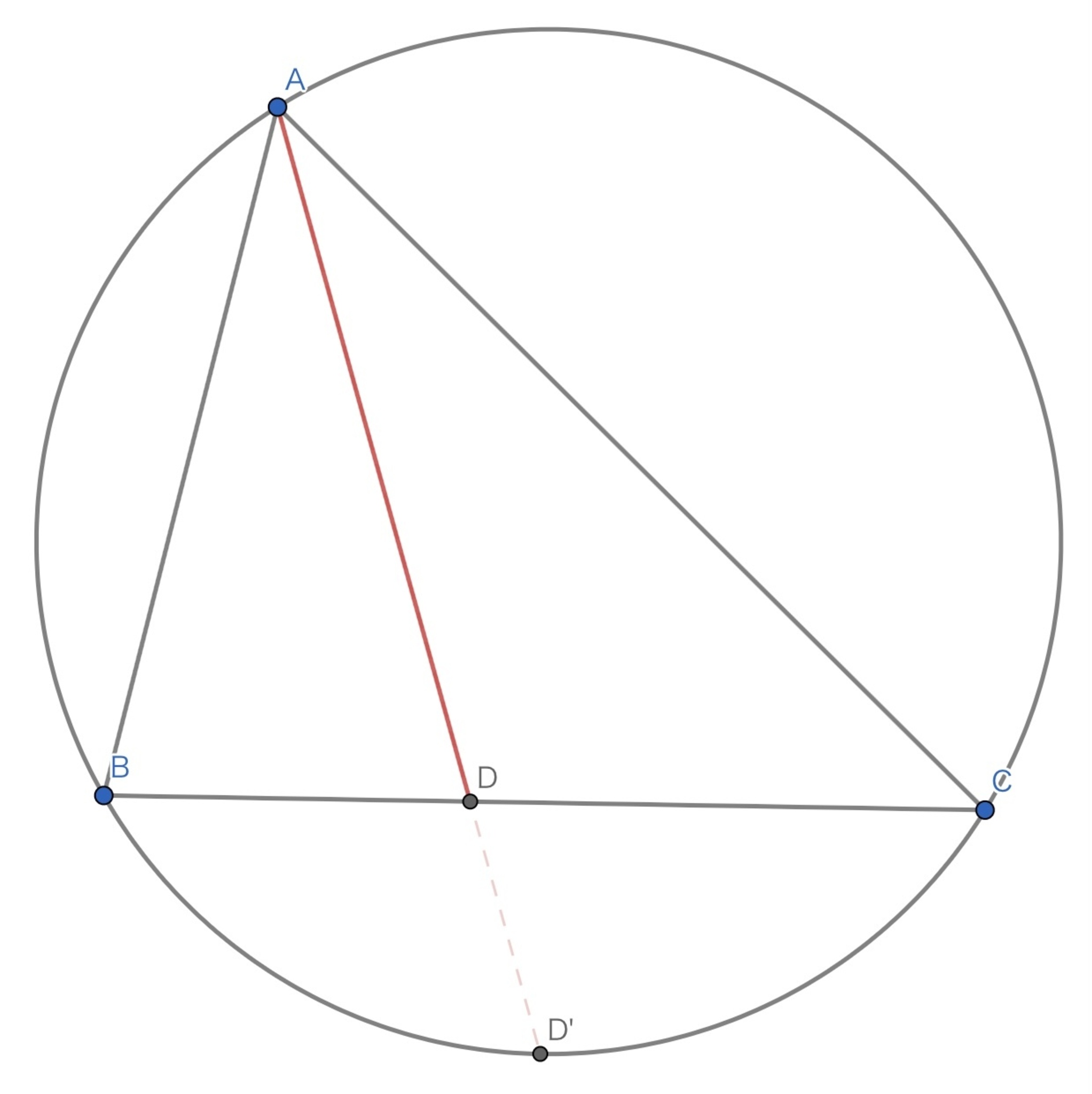角の二等分線
定理7より，$\dfrac{BD}{DC} \cdot \dfrac{BD}{DC} = \dfrac{AB}{AC} \cdot \dfrac{AB}{AC}$
よって，($0 \lt$)$\dfrac{BD}{DC} = \dfrac{AB}{AC}$
角の二等分線は，「自分自身と等角共役になる直線」と捉えられるので，反転共役で扱えそうです．
角の二等分線絡みの定理をもう一つやってみましょう．
$\angle BAC$の二等分線と直線$BC$の交点を$D$とおくと，
$AD^2 = AB \cdot AC - BD \cdot DC$
$AD^2 = AD(AD^{\star} - AD^{\star}) = AD \cdot AD^{\star} - AD \cdot DD^{\star} = AB \cdot AC - BD \cdot DC$
角の二等分線(反転共役後)
symmedian
等角共役線といえばやっぱりsymmedianですよね．
$B,C$における$\Gamma$の接線をそれぞれ$s_B,s_C$とおく．$s_B,s_C$の交点を$D$とすると，$AD$は$\triangle ABC$の$A$-symmedianである．
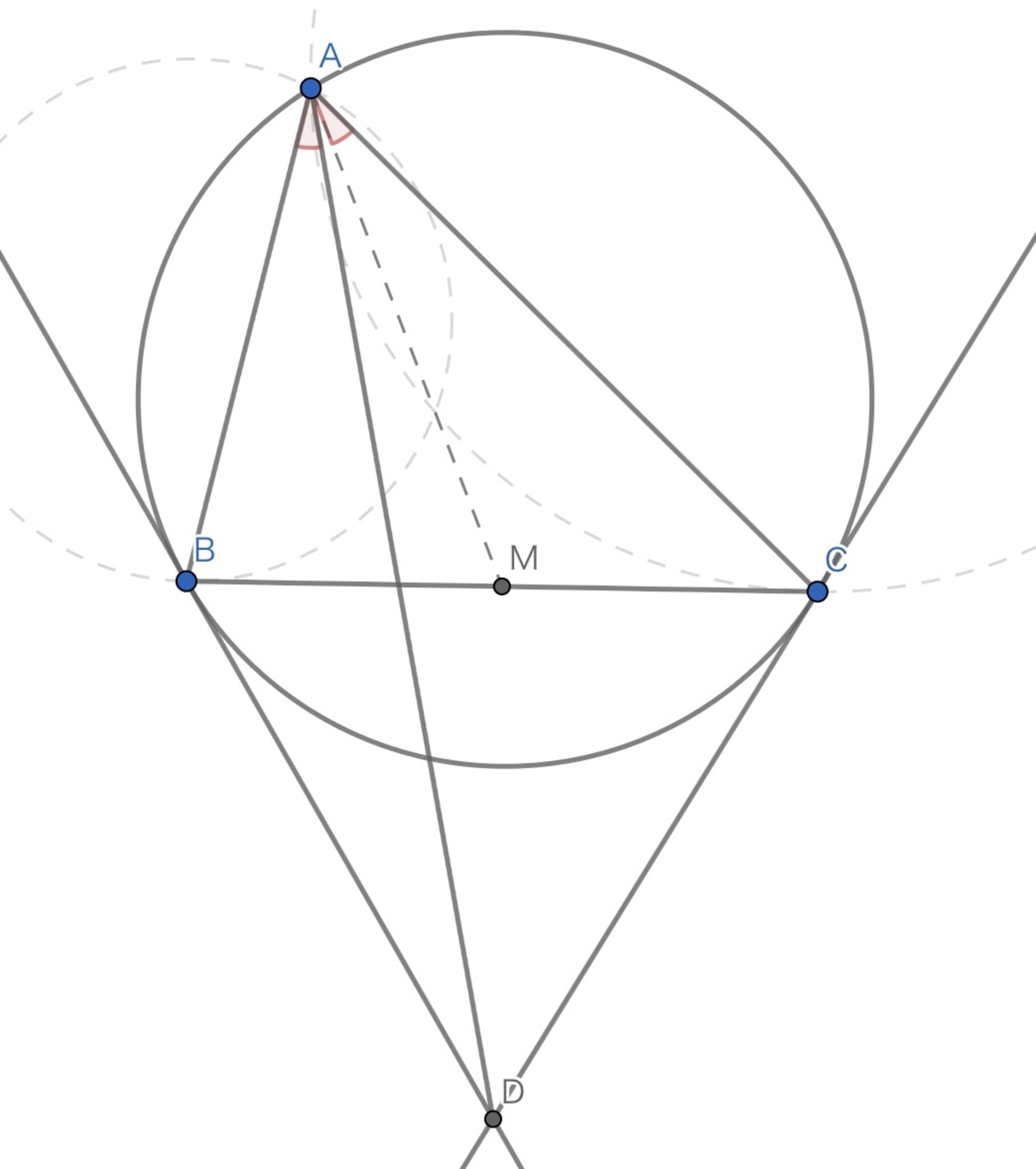symmedian
$s_B$は$B$で$\Gamma$に接する直線であるから，${s_B}^{\star}$は$C$で直線$BC$に接し，$A$を通る円である．
$s_C$は$C$で$\Gamma$に接する直線であるから，${s_C}^{\star}$は$B$で直線$BC$に接し，$A$を通る円である．
この$2$円の交点のうち，$A$でない方が$D^{\star}$である．
$AD^{\star}$と線分$BC$の交点を$M$とおくと，方べきの定理より，
$$MB^2 = MD^{\star} \cdot MA = MC^2$$
したがって，$M$は$BC$の中点であるから，$AD^{\star}$は$\triangle ABC$の$A$に関する中線で，その等角共役線$AD$は，$\triangle ABC$の$A$-symmedianである．
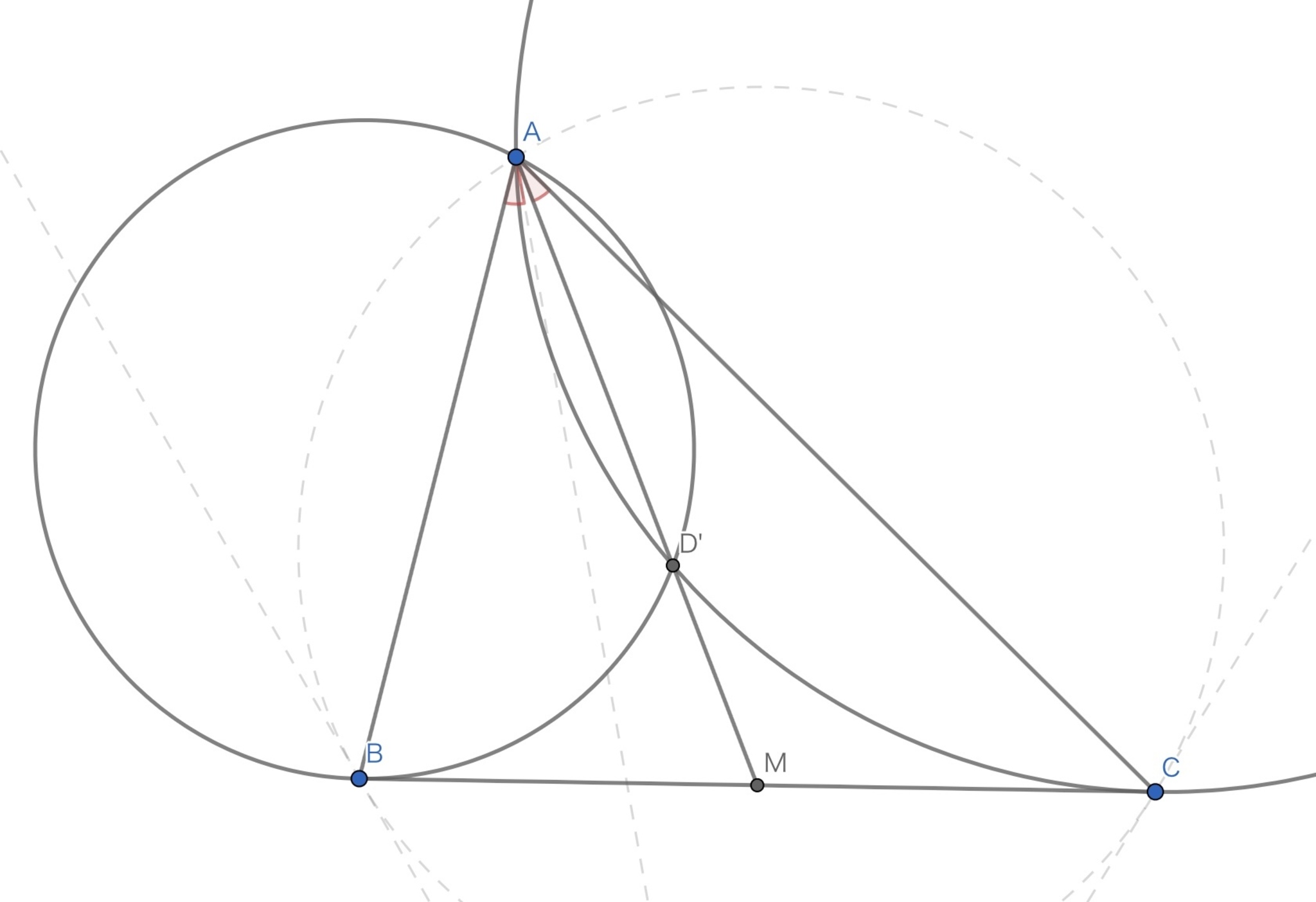symmedian(反転共役後)
symmedianでもっと遊びたい方は， Metachickさんの記事 も見てみましょう！
補遺
図7を見て，「$A$で反転すると良さそう」と思ったのがこの記事の始まりでした．
最後に
反転共役を使うと，色々な問題の見通しが良くなったり，記述がスッキリしたりします．
皆さんもぜひ，反転共役を使ってみてください！
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
