コラッツ予想と2進数列ビット長の有界性について
はじめに
いなばなつきさんの『 有界予想 』に触発されて、2進法で有界性について考えてみました。
2進3倍繰上げルール
コラッツ予想を2進法で考える、っていう過去2つの私の記事を読んでくださったみなさん、ありがとうございます。
まだご覧いただいていない方、リンク貼っときますのでよかったらご笑覧ください。
コラッツ予想と2進法
コラッツ予想を2進法で探求するための準備
要するに何が言いたいかっていうと、
- コラッツ予想で出てくる数列を2進法でゼロイチ表示をモノクロ表示すると見やすくていいね。
- さらに、”2で割る”のをやめて、”3n+1” の ”+1” を、”最下位ビットの繰上げ” で代用すると、いろいろと面白い性質が見えて来るよ。
って感じですかね。
2つめの『・』で言ってるやり方を『2進3倍繰上げルール』って勝手に呼んでます。(もっと適切な言い回しがあればご教示ください。)
とりあえず、『2進3倍繰上げルール』で、悪名高き『初期値27』について、その変化を図示します。
白は”0”、黒は”1”を表してます。
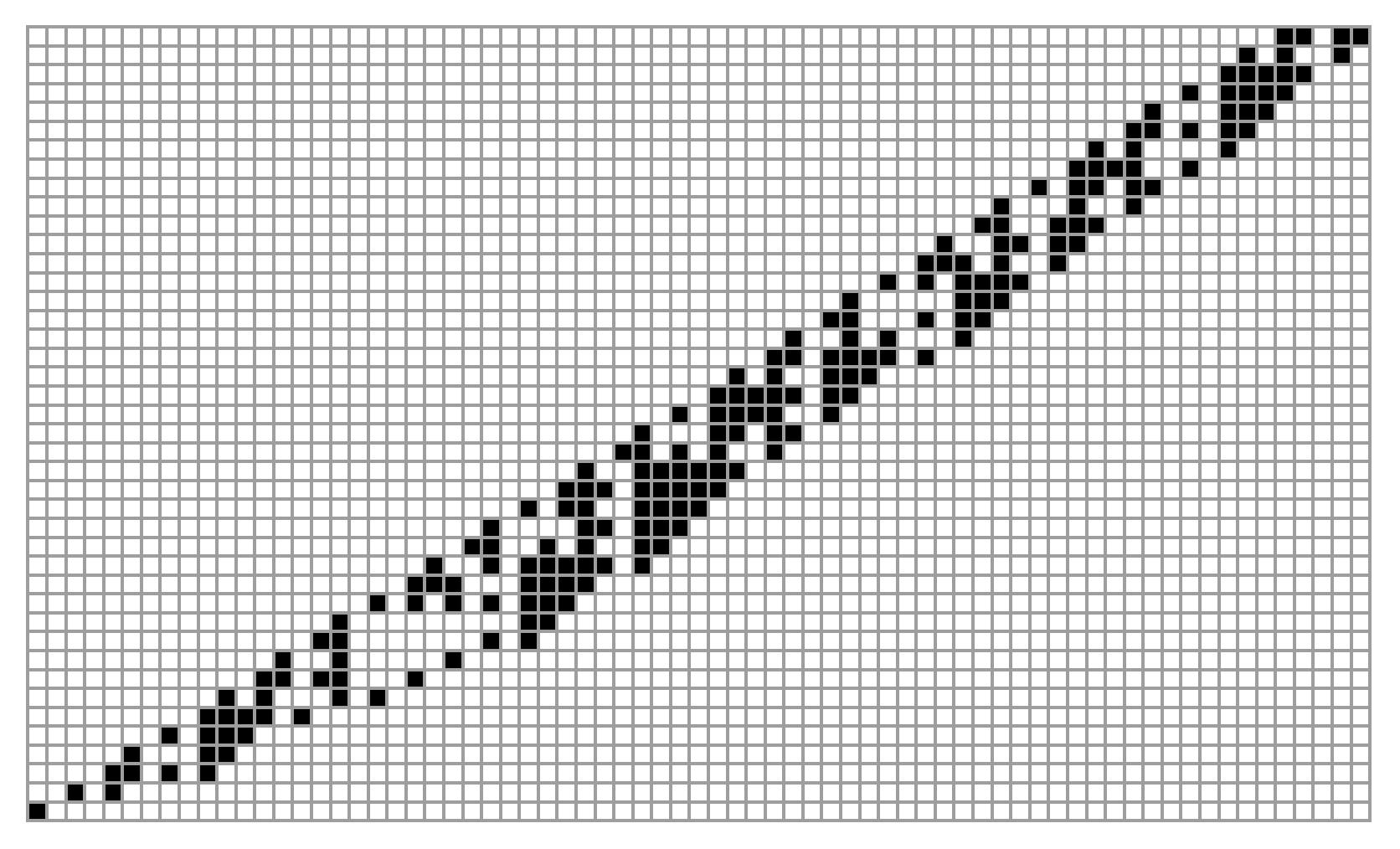 悪名高き『初期値27』
悪名高き『初期値27』
初期値10進法の27って、2進法だと”11011”ですね。
図の一番上の段、”11011”から始まって、
2段目、”3×27+1=82”で2進法だと”1010010”になってます。
そのまま2段目、最下位の”0”を無視すれば、”101001”って、10進法の82を2で割った”41”ってわけです。
以下、”3倍して右端の黒を繰り上げる”って操作を繰り返すことで、左右両端が黒のビット列が得られますが、それを10進法に直すと”コラッツ変換の奇数列”が得られる、って寸法です。
初期値27って、コラッツの手順で計算を繰り返すと、最大で9232なんていう馬鹿でかい数になって、電卓叩いていると不安になるんですよね。でも、そのうち2で割れることが増えてきて、『な〜んだ、やっぱり1になるじゃん』で終わるんですけど。
これをじーっと眺めていると、直角二等辺三角形の形に黒いやつが並んているところ、何ヶ所かありますよね。
これって、”3n+1”をした次、”2で割る”ことは1回しかできないよ、ってことを表してるんですね。
これも私、勝手に『黒三角の定理』って呼んでますけど、何かいい呼び方、どなたかご提案ください。
(^_^;)
ビット長の変化について
ようやく本題。
コラッツの手順で計算を繰り返していると、”2で割る”が1回しかできなかったり、いきなり何回も”2で割り”続けることができたり、普通に10進法の数を扱ってると、『なんじゃこりゃ!』って感じになりますよね。
けど、上の図のようなやつをいっぱい見てたら、『数値の大小より、ビット列の長さの方が大事じゃね?』って気持ちになって来たんです。
そこで、『コラッツの手順』で出てくる奇数を2進法表示した場合の、ビット列の長さが長くなるとき、短くなるときってどういうときか、整理してみました。
ある奇数を2進法で表したときのビット列の長さを$l$としますね。で、そのビット列に、『3n+1』に相当する『2進3倍繰上げ』の操作をほどこしてできるビット列(両端が”1”)の長さを$l'$とします。このとき、ビット列の長さ(ビット長)の変化$d$を、$d=l'-l$で定義します。
上の『悪名高き初期値27』の図を念頭に、次の表をご覧ください。
| ビット長の変化 $d$ | 最下位ビットが | 最下位ビットが | 最下位ビットが | |
|---|---|---|---|---|
| 1ビット左へ移動 | 2ビット左へ移動 | 3ビット以上左へ移動 | ||
| 最上位ビットが | 1ビット左へ移動 | ①$d=0$ | ②$d=-1$ | ③$d \leq -2$ |
| 最上位ビットが | 2ビット左へ移動 | ④$d=+1$ | ⑤$d=0$ | ⑥$d \leq -1$ |
先に結論を言ってしまうと、表から分かるように『ビット長が長くなるのは④のときだけ』なんですよね。
ちょっと詳しく見てみましょう。
最上位ビット(左端の黒)って、左にしか動きませんけど、動いても1個(①・②・③)か2個(④・⑤・⑥)なんですよね。
さらに言うと、『2個(2ビット)動く』っていうのが連続するのも2回まで。(『初期値27』の図の左端の黒の動きを追っかけてみてね。)
3回以上連続して2ビット動くのは、ビット長が1、つまり最終的な『1』になったときだけなんです。
この辺の事情、ちゃんと数式で説明することができるんでしょうけど、その辺りはみなさんにお任せします。コメントでお知らせいただけると嬉しいです。
じゃぁ、最下位ビット(右端の黒)はどうかって言うと、少なくとも1個は左に動く(①・④)んだけど、2個以上動く(②・③・⑤・⑥)ときって、ぜーったい、右端の黒の左隣は『0』なんですよね。しかも『0』と『1』の並び方によって『右端の黒が左に動く個数』が変わってくるってわけだ。
まぁ、下位のビット列が『$ \cdots $010101(←こいつが右端)』なんてなってた日にゃー、一気に『右端の黒』が左にいっぱい動いちゃう(③・⑥)わけですよ。これまた勝手に『しましましっぽの定理』と呼んでます。 前の記事 へのコメントでアレクサンダー鷹觜さんが上手いこと式にまとめてくれてました。アレクサンダー鷹觜さん、ありがとうございました。
ビット長の有界性?
いなばなつきさんの『 有界予想 』では、初期値の自然数と同じ数だけ『コラッツの手順』で変換を施す(『2で割る』も含めて)ってことが想定されているようですね。
私の『2進3倍繰上げルール』から得られる予想としては、『初期値のビット列の長さの数と同じ回数だけ『2進3倍繰上げ』をやると、ビット長は、長くなっても2倍までは行かないね』くらいしか言えないですね。ぜーんぜん、『有界』じゃないやー。
羊頭狗肉でごめんなさい。
でも、いなばなつきさんの『
有界予想
』で
『$ k=\lfloor\ln n\rfloor$としたときは有界ではありません』っていう議論は、要するに『10進法で考えたときの桁数』を考えてる、ってことですかね。私の『ぜーんぜん、有界じゃないやー』という結論と一緒って思っていいかな?
よくわかんないのが『従って、(連続体仮説を仮定すれば)$k$のオーダーは代数関数程度になるだろうことが分かります』って辺りなんですが、勉強します。参考になりそうな書籍や記事等をご紹介いただけるとありがたいです。
お詫びに代えて
2進法で考えるとき、ビット列を『上位部分(左側の黒のかたまり)と下位部分(右側の黒のかたまり;黒三角)とそれ以外』に分けて考える必要があるのかな、と思ってます。つまり、『”あたま”と”おしり”と”おなか”』ですね。
そんなふうに考えさせられてしまうような画像を2つほどアップします。
![初期値!FORMULA[14][1022385495][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FwKytUBgVuajIzMfu70W4.jpeg?alt=media) 初期値$2^{24}+1=16777217$
初期値$2^{24}+1=16777217$
こいつの真ん中を1個だけ黒に置き換えると、下のようになります。
![初期値!FORMULA[15][1785322155][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F7qV6YTL8abR0iIP4H8cL.jpeg?alt=media) 初期値$2^{24} + 2^{12} + 1=16781313$
初期値$2^{24} + 2^{12} + 1=16781313$
下位ビットからの『繰上げ』がない限り、上位ビット列は『3の累乗』倍されるんだってこととか、『おなか』に『しましま』($ \cdots 01010101 \cdots $)があると、『おなか』に『白三角』ができたり、『黒三角』ができたりするのがわかりますね。
結び
ここまでお付き合いいただき、ありがとうございました。
『2進3倍繰上げルール』に興味を持っていただけた方、『初期値◯でやってみてー』などのリクエストがありましたら、コメント欄でお知らせください。
近いうちに えどがわさんの一般化 と、私の考えてた一般化『n進(n+1)倍繰上げルール』との比較を記事にしてみたいと思ってます。よかったらまたご覧ください。
ありがとうございました!m(_ _)m
追記
『黒三角』について、縦方向に規則性が見られるのも興味深いので紹介します。
初期値$2^{24}-1=16777215$です。
![初期値!FORMULA[18][1280550871][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fa8BCIsWwSI6uqeji7jiW.jpeg?alt=media) 初期値$2^{24}-1=16777215$
初期値$2^{24}-1=16777215$
『黒三角』も下のはじっこまで来ると、『しましま』が出て来たりして、一気にビット長が短くなったりするんですよね。
『コラッツ予想』、まだまだ先は長いねぇ。
