幾何問題(2)の解説

はじめに

こちらの記事 で rieaaddlreiuuさん が僕の出した 幾何問題(2) を解かれたので、この記事で想定解を書きたいと思います。
まだ問題を見ていない方は一度 問題 を見てみてください！

解説

問題の図をもう一度載せます。

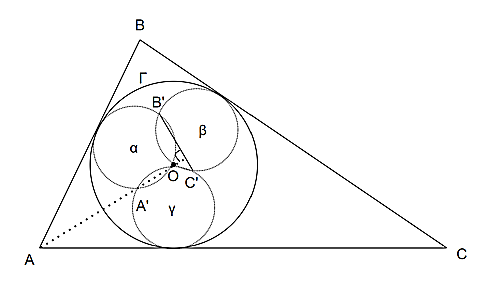問題
（円に$\alpha,\beta,\gamma$と名前を振りました。）
ここで、$\Gamma$を反転円としてこの図を反転させることを考えます。

$O,A,A'$が一直線上にある事の証明

まず円$\alpha$は直線$AB$,円$\beta$は直線$BC$,円$\gamma$は直線$AC$,となることがわかり、また逆に直線$AB$は円$\alpha$,直線$BC$は円$\beta$,直線$AC$は円$\gamma$,となることがわかる。
また$A$は直線$AB$と直線$AC$の交点なので、$A$を反転させた点は円$\alpha$,円$\gamma$の交点の$A'$となることがわかる。
よって反転の定義より、$O,A,A'$は一直線上にある。

$AA'\perp BC$の証明

$AA'$と$BC$の交点を$H$とおく。
$OA:OC=OC':OA'$より
$\triangle OAC \backsim \triangle OC'A' $であり
同様に$\triangle OCB \backsim \triangle OB'C' $
よって
$\d \angle A'HC'$
$\d =180^{\circ}-\angle HA'C'-\angle HC'A'$
$\d =180^{\circ}-\angle OA'C'-\angle OC'A'-\angle OC'B'$
$\d =180^{\circ}-\angle OCA-\angle OAC-\angle OBC$　（相似より）
$\d =180^{\circ}-\frac{180^{\circ}}{2}　（\triangle ABCの内角の\frac{1}{2}なので）$
$\d =90^{\circ}$
となり示された。

おわりに

反転（$+$ちょっと）で直交を示せるのはすごいなーと思ったので問題に出してみました！