放物線上をはね続けるボールの研究③焦点を通らない軌道と包絡線の話

はじめに

　この記事は、先日私が公開した

【Mathlog】放物線上をはね続けるボールの研究①フィボナッチ数が生えた話

【Mathlog】放物線上をはね続けるボールの研究②はね続ける条件の話

の記事や、子葉さんが公開した

【Mathlog】放物線上を跳ねる物体とフィボナッチ数

と関連のある内容となっています。

　時間のある方はこの記事と合わせてお読みいただくとよりいっそう楽しめると思います。

　これまでの記事では、
「放物線上を、その放物線の焦点を通る軌道で発射した質点は永久にはね続ける」
という現象を取り扱っていましたが、この記事では主に
「放物線上を、その放物線の焦点を通らない軌道で発射した質点が描く軌道」
を取り扱います。

　まずは実際に、「下に凸な放物線の上を、その放物線の焦点を通らない軌道で発射した質点が描く軌道」を $2$ パターンほどみてみましょう。

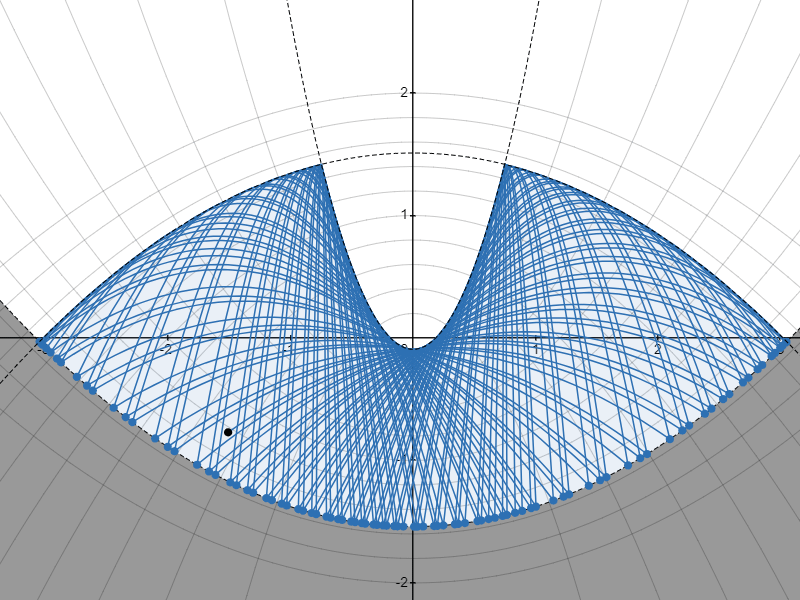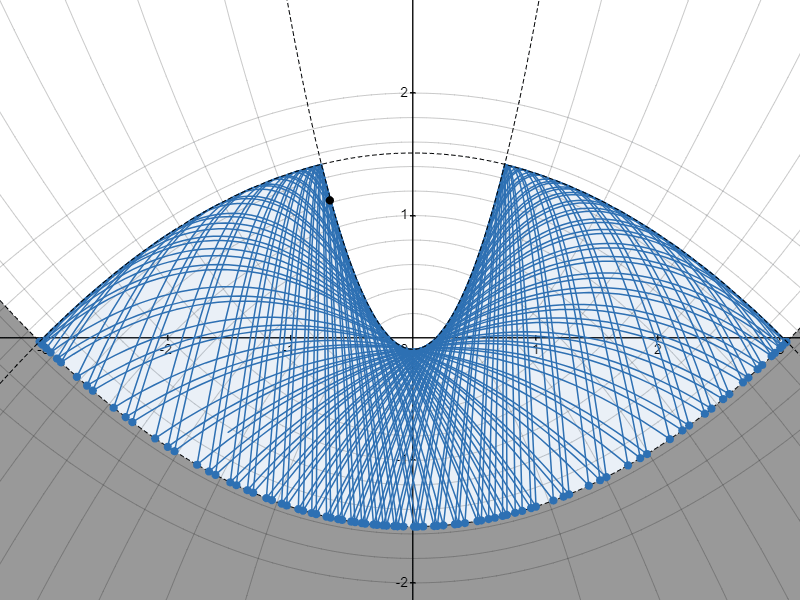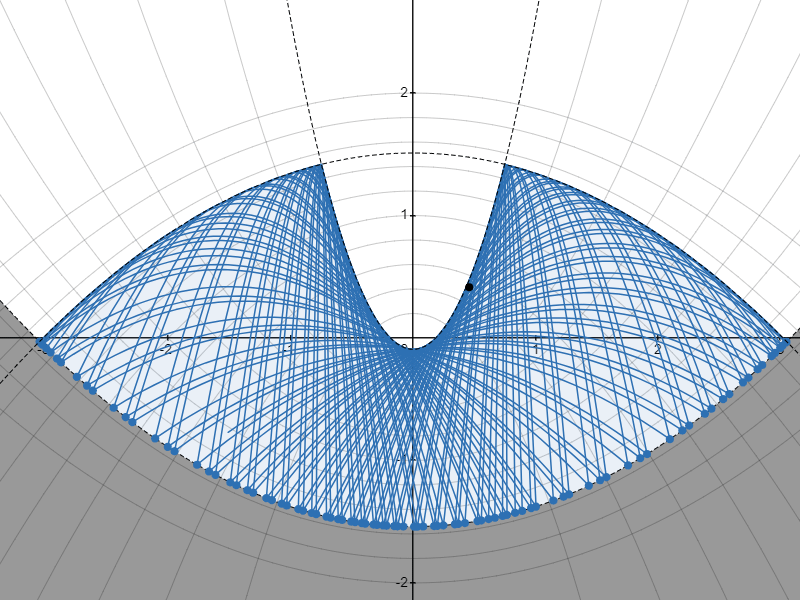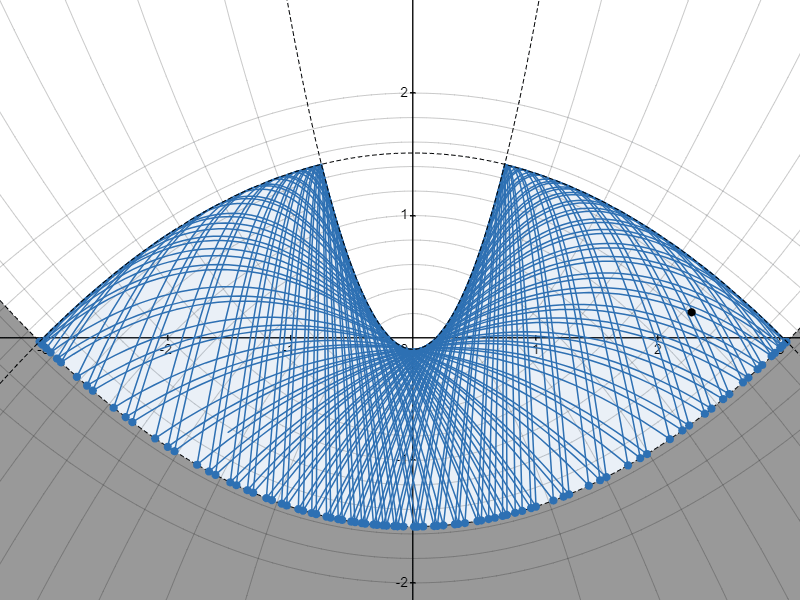包絡線のパターンA

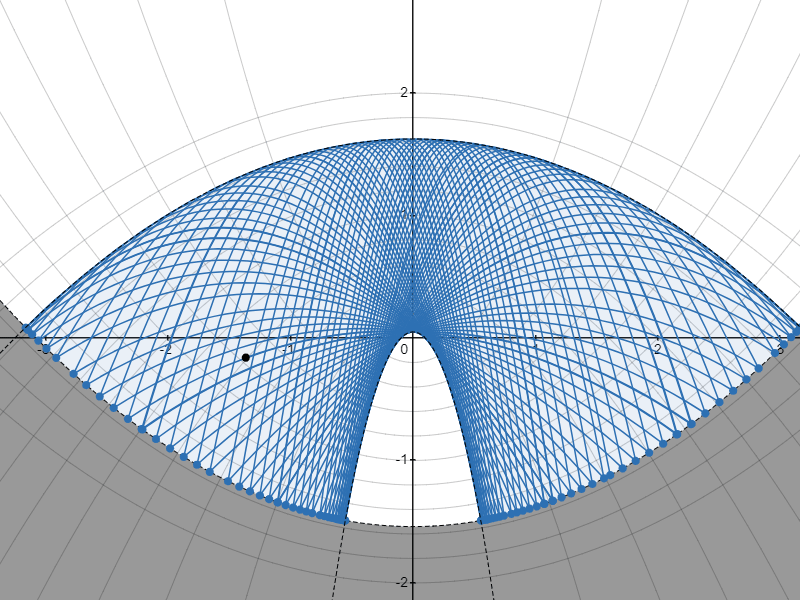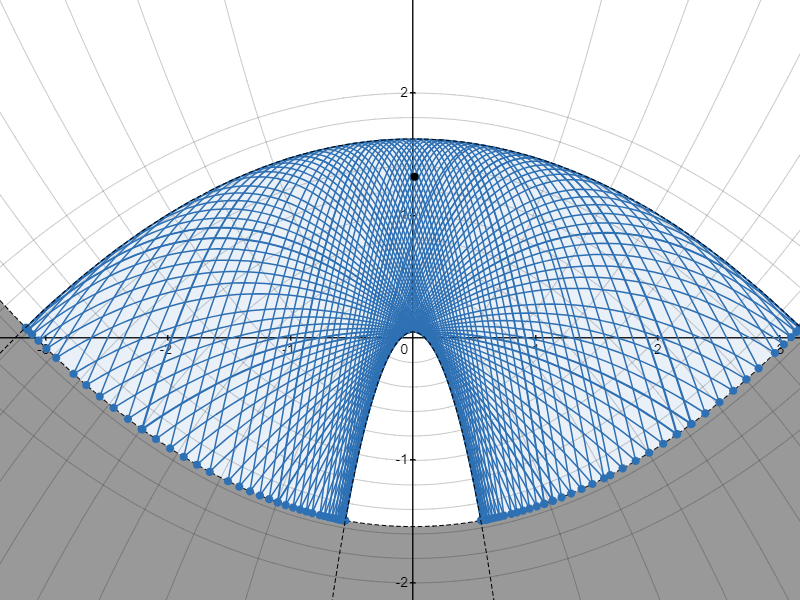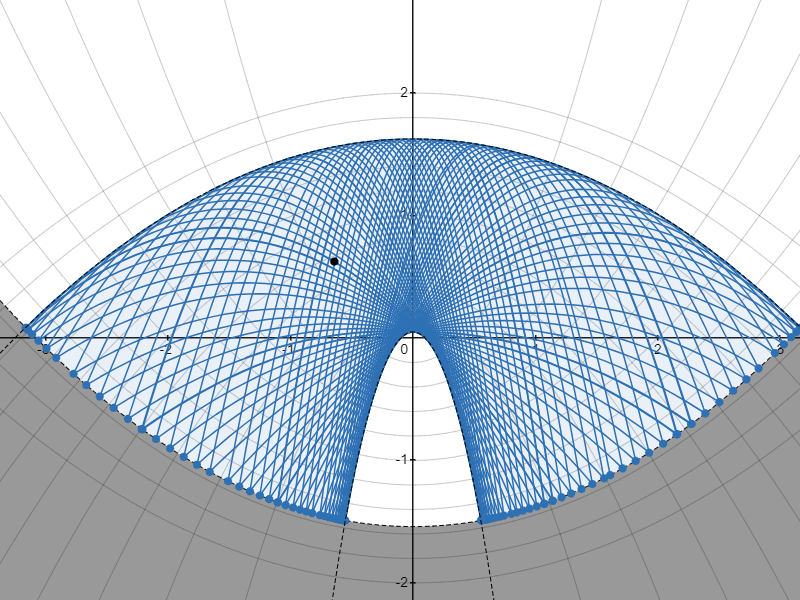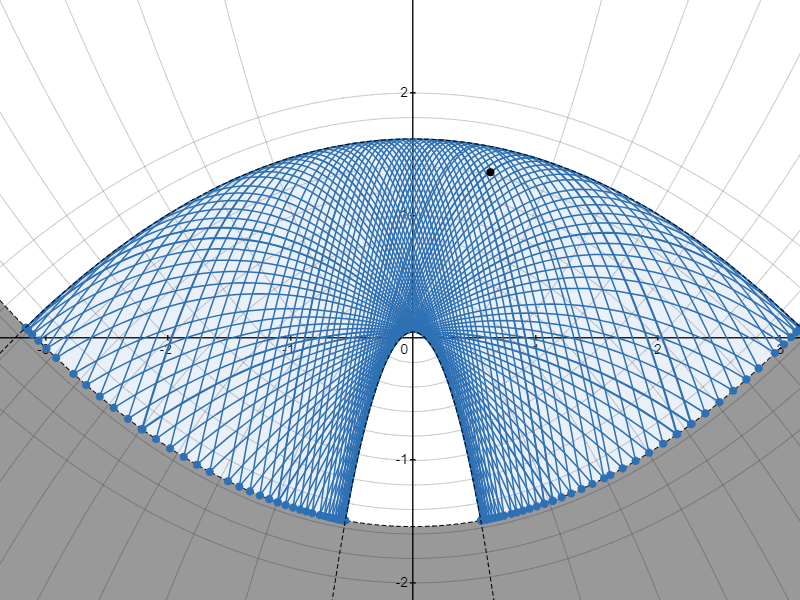包絡線のパターンB

　質点がはね続けると、質点の通り得る領域を囲む包絡線が現れるのが見えますね。
　@aoki_taichi さんは現れる包絡線が、ベースとなる放物線と焦点を同じくする放物線になるのではないかと予想されましたが……

複素変換でグニャリと曲げて長方形にしてみた。

ここから何が言えるのかはまだよくわからないけど、オレンジの曲線同士の交点が水平垂直に整列しているようにも見えますね… pic.twitter.com/AK5ndulB68

— Taichi AOKI (@aoki_taichi) February 9, 2024

……結論から言うと、その予想が正しかったことを証明できました!

　実際に動かせるDesmosファイルを用意しましたので、よろしければ実際に動かして体感してみてください。

Desmosファイルへのリンク

　この記事ではこれらの包絡線について主に取り上げます。
　これまでの記事と同様、直感的に理解しやすいように、$x$ 軸正方向を「右向き」、$y$ 軸負方向を「下向き」などと表現しています。
　座標平面上に重力加速度が一様に下向きに大きさ $1$ でかかっているものとします。衝突は完全弾性衝突(反発係数$=1$)とし、空気抵抗等は考慮しないものとします。また、反射のベースとなる放物線は原点に焦点を持ち、軸がy軸と重なるものとします。
　なお、これまでの記事とは違い、ベースとなる放物線は上に凸なものだけでなく、下に凸なものも含めて考えます。

包絡線のパターン

　まず、結果から書きます。

　では実際の様子を、「①下に凸な放物線上、 $Y_1>r_1$ 」「②下に凸な放物線上、 $Y_1< r_1$ 」「③上に凸な放物線上、 $Y_1>r_1$ 」「④上に凸な放物線上、 $Y_1< r_1$ 」のパターン別に見ていきましょう。

①下に凸な放物線上、 $Y_1>r_1$ のとき

　
①下に凸な放物線上、 $Y_1>r_1$ のとき

　原点焦点で ${\displaystyle \left(0,\frac{Y_1\pm r_1}{2}\right)}$ を頂点とする放物線はいずれも上に凸となり、間に挟まれた領域を通過する軌道となっています。

②下に凸な放物線上、 $Y_1< r_1$ のとき

②下に凸な放物線上、 $Y_1< r_1$ のとき

　原点焦点で ${\displaystyle \left(0,\frac{Y_1+ r_1}{2}\right)}$ を頂点とする放物線は上に凸、${\displaystyle \left(0,\frac{Y_1- r_1}{2}\right)}$ を頂点とする放物線は下に凸となり、アリジゴクの巣のような形の領域を通過する軌道となっています。

③上に凸な放物線上、 $Y_1>r_1$ のとき

③上に凸な放物線上、 $Y_1>r_1$ のとき

　原点焦点で ${\displaystyle \left(0,\frac{Y_1\pm r_1}{2}\right)}$ を頂点とする放物線はいずれも上に凸となり、間に挟まれた領域を通過する軌道となっています。

　なお、ベースとなる放物線が ${\displaystyle \left(0,\frac{Y_1- r_1}{2}\right)}$ を頂点とする放物線よりさらに下にある場合には、質点は一度も反射することなく奈落へ落ちていくことになります。

④上に凸な放物線上、 $Y_1< r_1$ のとき

④上に凸な放物線上、 $Y_1< r_1$ のとき

　原点焦点で ${\displaystyle \left(0,\frac{Y_1+ r_1}{2}\right)}$ を頂点とする放物線は上に凸、${\displaystyle \left(0,\frac{Y_1- r_1}{2}\right)}$ を頂点とする放物線は下に凸となり、アリジゴクの巣のような形の領域を通過する軌道となっています。

　ベースとなる放物線の位置によっては、右向きに発射した質点が途中で左向きになったりします。

　なお、$Y_1=r_1$ のときは永久にはね続ける軌道になります。

包絡線

　それではここから、これらの性質が成り立つことを数式で確認していきたいと思います。

放物線族

　$a\ne0$とします。原点に焦点を持ち、 $(0,a)$ に頂点を持つ放物線の方程式は

　$y=-\dfrac{x^2}{4a}+a$

　と書くことができます。
　このとき、$a>0$ のときは上に凸な放物線となります。このような放物線をまとめて $C_{+}$ と呼ぶことにします。
　逆に、$a<0$ のときは下に凸な放物線となります。このような放物線をまとめて $C_{-}$ と呼ぶことにします。

　すると、$C_{+}$ と $C_{-}$ は必ず直交します。

　また、$xy$ 平面上の点のうち、$x\ne0$ の点については、対応する$C_{+},C_{-}$ の放物線がそれぞれ　$1$ つ定まります。

前提条件

　ここからは、平面全体に下向きに $1$ の重力加速度がかかっている座標平面上で、座標 $(x_0,y_0)$ から速度 $\vec{v_0}=\pmatrix{v_x\\v_y}$ で発射した質点が、原点を焦点に持つ放物線上を弾性衝突し続けるときの軌道について考えます。
　場合分けを減らすため、$\textcolor{red}{x_0<0,v_x\ne0}$ の場合のみ考えることにします。

　$(x_0,y_0)$ に対応する$C_{+},C_{-}$ の放物線をそれぞれ $C_P,C_Q$ と呼ぶことにし、頂点をそれぞれ $(0,P),(0,Q)$ します。$(P>0,Q<0)$

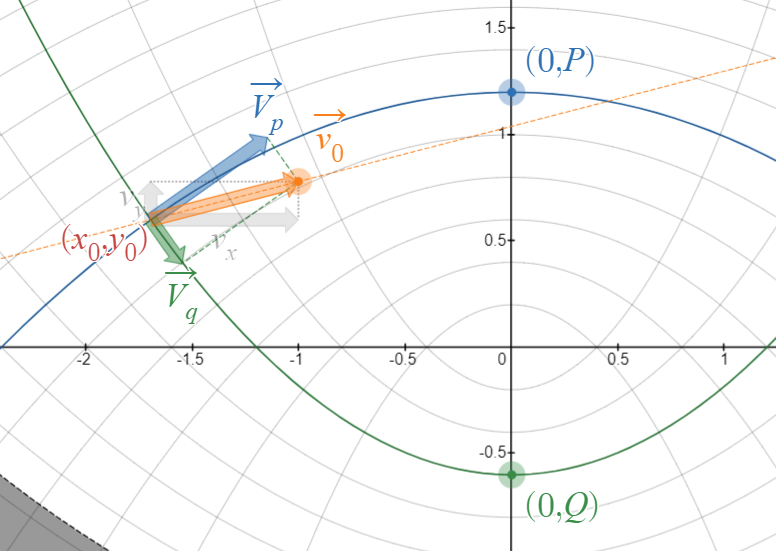記号の説明

　$x_0,y_0$ を $P,Q$ で表すとこうなります。

　次に、$\vec{v_0}$ を、$C_P$ の $(x_0,y_0)$ における接線右向きのベクトル $\vec{V_P}$ と、$C_Q$ の $(x_0,y_0)$ における接線右向きのベクトル $\vec{V_Q}$ に分解します。(図 $7$ 参照)

　$(x_0,y_0)$ における $C_P,C_Q$ の傾きがそれぞれ ${\displaystyle \frac{\sqrt{-Q}}{\sqrt{P}},\frac{-\sqrt{P}}{\sqrt{-Q}}}$となることから、適切に $v_p,v_q$　をとることで次のように表すことができます。

　ベクトルの成分を比較することで $v_x,v_y,v_p,v_q$ の次の関係がわかります。

包絡線の検証

　原点を焦点に持つ放物線　${\displaystyle y=-\frac{x^2}{4A}+A}$ が放物線 ${\displaystyle y=y_0+v_y\left(\frac{x-x_0}{v_x}\right)-\frac{1}{2}\left(\frac{x-x_0}{v_x}\right)^2}$ と接するような $A(\ne0)$ を求めたい。$y$ を消去して

　${\displaystyle -\frac{x^2}{4A}+A=y_0+v_y\left(\frac{x-x_0}{v_x}\right)-\frac{1}{2}\left(\frac{x-x_0}{v_x}\right)^2}$

　両辺に $4Av_x^2$ を乗じて

　${\displaystyle -x^2v_x^2+4A^2v_x^2=4Ay_0v_x^2+4Av_xv_y\left(x-x_0\right)-2A\left(x-x_0\right)^2}$

　${\displaystyle v_x^2x^2-4A^2v_x^2+4Ay_0v_x^2+4Av_xv_y\left(x-x_0\right)-2A\left(x-x_0\right)^2=0}$

　${\displaystyle (v_x^2-2A)x^2+4A(v_xv_y+x_0)x-4A^2v_x^2+4Ay_0v_x^2-4Av_xv_yx_0-2Ax_0^2=0}$

　これを $x$ の $2$ 次方程式と見れば、解は $2$ つの放物線の交点の座標を表すのであるから、この方程式の判別式 $D=0$ となるような $A$ を求めればよい。

　${\displaystyle \begin{align} \frac{D}{4}&=4A^2(v_xv_y+x_0)^2-(v_x^2-2A)(-4A^2v_x^2+4Ay_0v_x^2-4Av_xv_yx_0-2Ax_0^2)\\ &=2A\left(2A(v_xv_y+x_0)^2-(v_x^2-2A)(-2Av_x^2+2y_0v_x^2-2v_xv_yx_0-x_0^2)\right) \end{align}}$

　$D=0,A\ne0$ より
　${\displaystyle 2A(v_xv_y+x_0)^2-(v_x^2-2A)(-2Av_x^2+2y_0v_x^2-2v_xv_yx_0-x_0^2)=0}$

　${\displaystyle 2Av_x^2v_y^2\textcolor{red}{+4Ax_0v_xv_y}\textcolor{blue}{+2Ax_0^2}+2Av_x^4-2y_0v_x^4+2v_x^3v_yx_0+v_x^2x_0^2-4A^2v_x^2+4Ay_0v_x^2\textcolor{red}{-4Ax_0v_xv_y}\textcolor{blue}{-2Ax_0^2}=0}$

　${\displaystyle -v_x^2\left(4A^2-2A\left(v_y^2+v_x^2+2y_0\right)+2y_0v_x^2-2v_xv_yx_0-x_0^2\right)=0}$

　$v_x\ne0$ より

　${\displaystyle 4A^2-2A\left(v_y^2+v_x^2+2y_0\right)+2y_0v_x^2-2v_xv_yx_0-x_0^2=0}$

　${\displaystyle A=\frac{v_y^2+v_x^2+2y_0\pm\sqrt{\left(v_y^2+v_x^2+2y_0\right)^2-4\left(2y_0v_x^2-2v_xv_yx_0-x_0^2\right)}}{4}}$

　
　つぎに、$v_x,v_y,x_0,y_0$ を $v_p,v_q,P,Q$ で書き換える。(座標変換のアナロジー)

　${\displaystyle \begin{align} v_x^2+v_y^2&=\left(v_p\sqrt{P}+v_q\sqrt{-Q}\right)^2+\left(v_p\sqrt{-Q}-v_q\sqrt{P}\right)^2\\ &=v_p^2P+2v_pv_q\sqrt{-PQ}-v_q^2Q-v_p^2Q-2v_pv_q\sqrt{-PQ}+v_q^2P\\ &=\left(v_p^2+v_q^2\right)\left(P-Q\right) \end{align} }$

などを使って

　${\displaystyle \begin{align} A=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm\sqrt{\left(\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\right)^2-4\left(\textcolor{red}{2(P+Q)(v_p\sqrt{P}+v_q\sqrt{-Q})^2-2(v_p\sqrt{P}+v_q\sqrt{-Q})(v_p\sqrt{-Q}-v_q\sqrt{P})\cdot(-2\sqrt{-PQ})+4PQ}\right)}}{4} \end{align} }$

　赤字の部分を抜き出して変形していく。

　${\displaystyle \begin{align} &\textcolor{red}{2(P+Q)(v_p\sqrt{P}+v_q\sqrt{-Q})^2-2(v_p\sqrt{P}+v_q\sqrt{-Q})(v_p\sqrt{-Q}-v_q\sqrt{P})\cdot(-2\sqrt{-PQ})+4PQ}\\ &=2(P+Q)(v_p^2P-v_q^2Q+2v_p v_q\sqrt{-PQ})+2(v_p^2\sqrt{-PQ}-v_q^2\sqrt{-PQ}-v_pv_qP-v_pv_qQ)\cdot2\sqrt{-PQ}+4PQ\\ &=2P^2v_p^2-2PQv_q^2\textcolor{red}{+4Pv_p v_q\sqrt{-PQ}}+2PQv_p^2-2Q^2v_q^2\textcolor{blue}{+4Qv_p v_q\sqrt{-PQ}}-4PQv_p^2+4PQv_q^2\textcolor{red}{-4Pv_pv_q\sqrt{-PQ}}\textcolor{blue}{-4Qv_pv_q\sqrt{-PQ}}+4PQ\\ &=2P^2v_p^2-2PQv_q^2+2PQv_p^2-2Q^2v_q^2-4PQv_p^2+4PQv_q^2+4PQ\\ &=2P^2v_p^2-2Q^2v_q^2-2PQv_p^2+2PQv_q^2+4PQ\\ &=2(v_p^2P+v_q^2Q)(P-Q)+4PQ\\ \end{align} }$

　元の式に戻すと

　${\displaystyle \begin{align} A&=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm\sqrt{\left(\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\right)^2-4\left(\textcolor{red}{2(v_p^2P+v_q^2Q)(P-Q)+4PQ}\right)}}{4}\\ &=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm\sqrt{\left(v_p^2+v_q^2\right)^2\left(P-Q\right)^2+4\left(v_p^2+v_q^2\right)\left(P^2-Q^2\right)+4(P+Q)^2-16PQ-8v_p^2P^2-8v_q^2PQ+8v_p^2PQ+8v_q^2Q^2}}{4}\\ &=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm\sqrt{\left(v_p^2+v_q^2\right)^2\left(P-Q\right)^2+4\left(v_p^2+v_q^2\right)\left(P-Q\right)^2+4(P-Q)^2+8PQv_p^2+8PQv_q^2-8Q^2v_p^2-8Q^2v_q^2-8v_p^2P^2-8v_q^2PQ+8v_p^2PQ+8v_q^2Q^2}}{4}\\ &=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm(P-Q)\sqrt{\left(v_p^2+v_q^2\right)^2+4\left(v_p^2+v_q^2\right)+4-8v_p^2}}{4}\\ &=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)\pm(P-Q)\sqrt{\left(v_p^2+v_q^2\right)^2-4\left(v_p^2-v_q^2\right)+4}}{4}\\ \end{align} }$

　ここで、$v_p,v_q$ はいずれも $2$ 乗の形になっていることに注目してください。
　つまり、$v_p$ を $-v_p$ に置き換えたり、 $v_q$ を $-v_q$ に置き換えたりしても $A$ の $2$ 解は不変、すなわち不変量ということになります。

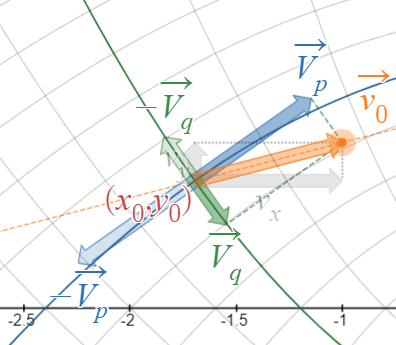符号を逆にする

　$C_{+}$ 又は $C_{-}$ で質点が反射した場合、$v_q$ 又は $v_p$ の符号が逆になることと合わせて、「$C_{+}$ 又は $C_{-}$ で質点が反射しても、『原点を通り質点の軌跡に接する $2$ つの放物線』は不変である」ことが言えたことになります。

焦点の原点からの距離や、準線の $y$ 座標を求める

　質点の描く放物線の焦点を $F_0$ と、準線の $y$ 座標を $Y_0$ として、$F_0,Y_0$ を $x_0,y_0,v_x,v_y$ の式で表すことを考えます。

　まず頂点の座標を求めます。

　${\displaystyle \begin{align} y&=y_0+v_y\left(\frac{x-x_0}{v_x}\right)-\frac{1}{2}\left(\frac{x-x_0}{v_x}\right)^2\\ &=-\frac{1}{2v_x^2}\left(\left(x-(x_0+v_xv_y)\right)^2\right)+y_0+\frac{v_y^2}{2} \end{align} }$

と変形できるので頂点は $\left(x_0+v_xv_y,y_0+\frac{v_y^2}{2}\right)$

　$x$ の $2$ 次の係数から焦点までの距離は $\dfrac{v_x^2}{2}$ とわかるので、

とわかります。

　つぎに、$v_x,v_y,x_0,y_0$ を $v_p,v_q,P,Q$ で書き換えます。(座標変換のアナロジー)

$Y_0$ について

　${\displaystyle \begin{align} Y_0&=(P+Q)+\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)}{2}\\ &=\frac{\left(v_p^2+v_q^2\right)\left(P-Q\right)+2(P+Q)}{2} \end{align}}$

　$v_p,v_q$ はいずれも $2$ 乗の形になっていることに注目してください。
　つまり、$v_p$ を $-v_p$ に置き換えたり、 $v_q$ を $-v_q$ に置き換えたりしても $Y_0$ は不変、すなわち不変量ということになります。
　$C_{+}$ 又は $C_{-}$ で質点が反射した場合、$v_q$ 又は $v_p$ の符号が逆になることと合わせて、「$C_{+}$ 又は $C_{-}$ で質点が反射しても、『質点が描く放物線の準線』は不変である」ことが言えたことになります。

$F_0$ について

　$F_0\left(\textcolor{red}{-2\sqrt{-PQ}+(v_p\sqrt{P}+v_q\sqrt{-Q})(v_p\sqrt{-Q}-v_q\sqrt{P})},\textcolor{blue}{(P+Q)+\dfrac{-(v_p\sqrt{P}+v_q\sqrt{-Q})^2+(v_p\sqrt{-Q}-v_q\sqrt{P})^2}{2}}\right)$

　$x$ 座標について

　${\displaystyle \begin{align} &\textcolor{red}{-2\sqrt{-PQ}+(v_p\sqrt{P}+v_q\sqrt{-Q})(v_p\sqrt{-Q}-v_q\sqrt{P})}\\ &=-2\sqrt{-PQ}+v_p^2\sqrt{-PQ}-v_q^2\sqrt{-PQ}-v_pv_qP-v_pv_qQ\\ &=-(2-v_p^2+v_q^2)\sqrt{-PQ}-v_pv_q(P+Q)\\ \end{align} }$

　$y$ 座標について

　${\displaystyle \begin{align} &\textcolor{blue}{(P+Q)+\dfrac{-(v_p\sqrt{P}+v_q\sqrt{-Q})^2+(v_p\sqrt{-Q}-v_q\sqrt{P})^2}{2}}\\ &=(P+Q)+\dfrac{-v_p^2P-2v_pv_q\sqrt{-PQ}+v_q^2Q-v_p^2Q-2v_pv_q\sqrt{-PQ}+v_q^2P}{2}\\ &=\dfrac{(2-v_p^2+v_q^2)(P+Q)-4v_pv_q\sqrt{-PQ}}{2}\\ \end{align} }$

$F_0$ の原点からの距離を $r_0$ とすると

　${\displaystyle \begin{align} r_0^2&=\left(-(2-v_p^2+v_q^2)\sqrt{-PQ}-v_pv_q(P+Q)\right)^2+\left(\frac{(2-v_p^2+v_q^2)(P+Q)-4v_pv_q\sqrt{-PQ}}{2}\right)^2\\ &=\frac{1}{4}\left( -4(2-v_p^2+v_q^2)^2PQ\textcolor{red}{+8(2-v_p^2+v_q^2)\sqrt{-PQ}v_pv_q(P+Q)}+4v_p^2v_q^2(P+Q)^2 +(2-v_p^2+v_q^2)^2(P+Q)^2\textcolor{red}{-8(2-v_p^2+v_q^2)(P+Q)v_pv_q\sqrt{-PQ}}-16v_p^2v_q^2PQ \right)\\ &=\frac{1}{4}\left( -4(2-v_p^2+v_q^2)^2PQ+4v_p^2v_q^2(P+Q)^2 +(2-v_p^2+v_q^2)^2(P+Q)^2-16v_p^2v_q^2PQ \right)\\ &=\frac{1}{4}(P-Q)^2\left( 4v_p^2v_q^2+4+v_p^4+v_q^4-4v_p^2+4v_q^2-2v_p^2v_q^2 \right)\\ &=\frac{1}{4}(P-Q)^2\left((v_p^2+v_q^2)^2 -4(v_p^2-v_q^2)+4 \right)\\ \end{align} }$

${\displaystyle \therefore r_0=\frac{(P-Q)\sqrt{(v_p^2+v_q^2)^2 -4(v_p^2-v_q^2)+4 }}{2} }$

　$v_p,v_q$ はいずれも $2$ 乗の形になっていることに注目してください。
　つまり、$v_p$ を $-v_p$ に置き換えたり、 $v_q$ を $-v_q$ に置き換えたりしても $r_0$ は不変、すなわち不変量ということになります。
　$C_{+}$ 又は $C_{-}$ で質点が反射した場合、$v_q$ 又は $v_p$ の符号が逆になることと合わせて、「$C_{+}$ 又は $C_{-}$ で質点が反射しても、『質点が描く放物線の焦点の原点からの距離』は不変である」ことが言えたことになります。

$A,Y_0,r_0$ の関係

　それでは、ここまでに得られた $A,Y_0,r_0$ の式を並べてみましょう。

　明らかに次の関係があることがわかりますね!

　これで冒頭の性質を数式から確かめたことになります。

さいごに

　これで今回の記事はおしまいです。
　実は、先にご紹介したDesmosファイルですが、隠し機能がありまして

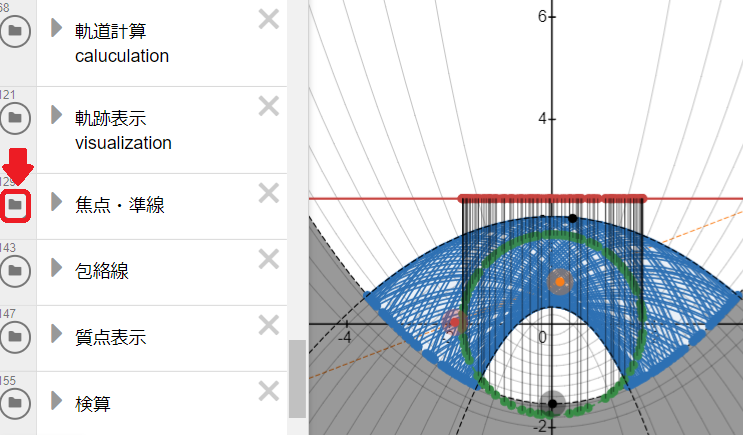画像の名前

　「焦点・準線」フォルダの表示をオンにすることで、軌道の焦点・準線を確認することができますので、いろいろと試してみていただければと思います。

Desmosファイルへのリンク(再掲)

　当初、不思議な模様にみえていたものが、放物線の焦点と準線に注目してみると、背景にある実にシンプルで美しい関係が現れてきて、実に感動的でありました。
　また、この記事では数式で証明する流れでしたが、幾何的に証明することもできるのではないかと思います。
　例えば、衝突点を $P$ 、衝突前後の軌道となる放物線の焦点をそれぞれ $F_1,F_2$ 、ベースとなる放物線の焦点を $F_b$ とおくと、「"$P$ と $F_1$ の距離" と "$P$ と $F_2$ の距離" は同じ」という性質がありますが、これは幾何的にも証明できそうです。また、この性質から、「$F_1$ と $F_2$ をつなぐ線分の垂直二等分線上に $F_b$ があること」を導くことが可能ですし、そこから軌道の焦点が円を描くことも導くことができます。
　これらの現象を、力学的エネルギーとからめて物理的に解釈することも楽しそうです。
　もし何か面白い性質や新しい解釈を見つけたら教えていただければ幸いです!