量子コンピュータにおける素因数分解(6)：量子ゲートの実装

はじめに

この記事は量子コンピュータによる素因数分解のアルゴリズムである「Shorのアルゴリズム」の解説記事第6回目です。1-5回目は以下：

1. 量子コンピュータにおける素因数分解(1): 加算器
2. 量子コンピュータにおける素因数分解(2): べき剰余
3. 量子コンピュータにおける素因数分解(3): 量子フーリエ変換
4. 量子コンピュータにおける素因数分解(4): アルゴリズムの方針 & 関連定理
5. 量子コンピュータにおける素因数分解(5): 位数推定と量子干渉

本記事では本シリーズの締めくくりとして、今まで紹介した基本的な量子ゲートをいかに物理系で実現するかに関して触れたいと思います。物理学の基礎的な知識が必要な部分がありますし、また議論がいい加減な部分があります（筆者の理解不足によります）。数学徒の方々にはもしかしたら読みにくいかもしれませんがご容赦ください。雰囲気だけ感じてくれれば、と思います。

ここでは2つの実装方法を紹介します。

ひとつは原子のラビ振動を用いた量子ゲートです。これは他の量子ゲートの実装の理解の助けにもなるので紹介します。ただしこのような方法を用いた量子コンピュータが実際に稼働しているかはわかりません。

もうひとつは超伝導ループ・ジョセフソン接合を用いた実現方法ですNielsenHosoyaChoiMukai。これはGoogleのSycamoreプロセッサやIBMの量子コンピュータチップHeronでも採用されている方法であり、現実的な実現方法ですChoiMukai。ただし細かいセットアップは違うと思います。

どちらも発想は同じで、近似的な2準位系を作り、何らかのハミルトニアンを印加することで2準位間の相対位相・重みを変化させ、必要なユニタリー変換を実現します。

シュレーディンガー方程式とBornの規則

本記事ではシュレーディンガー方程式（Schrödinger Equation, SE）を解きます。そのため本章ではその解き方に関して簡単に述べておきます。すでに馴染みがある方は飛ばして「量子ゲートの実装」に進んでください。

シュレーディンガー方程式（SE）

SEは以下の方程式です：

$\psi$は波動関数と呼ばれ、場所$\boldsymbol{x}$と時刻$t$に依存します。この波動関数で記述される物体が場所$\boldsymbol x$と時刻$t$に存在する確率密度は$|\psi(\boldsymbol{x},t)|^2$で表されます。$\hat H$はハミルトニアンと呼ばれ、エネルギーを固有値にもつ演算子です。ハミルトニアンの第1項は運動エネルギー、第2項はポテンシャルエネルギーに対応します。

波動関数は物体に関するすべての情報を担います。時刻$t=0$における波動関数$\psi(\boldsymbol{x},t=0)$が与えられれば、SEを解くことにより任意の時刻での波動関数$\psi(\boldsymbol{x},t)$がわかります。すなわちSEは物体の量子力学的状態の時間発展を記述する方程式です。

SEを解くためには、エネルギーの固有値・固有状態を求めればよいです。すなわち以下の方程式
\begin{align} \hspace{1.5cm} \hat H\phi_n(\boldsymbol{x})=E_n\phi_n(\boldsymbol{x}) \end{align}
を解けばよいです。簡単のためここでは$n$は整数とします。これを解くことで$\{E_n,\phi_n(\boldsymbol{x})\}_{n\in \mathbb{Z}}$のセットを得ます。$H$はエルミート演算子であり、$\phi_n$は完全系をなします。

$t=0$での波動関数$\psi_0(\boldsymbol{x})$が与えられたとします。このとき$\psi_0$を完全系$\phi_n$で展開します：
\begin{align} \hspace{1.5cm} \psi_0(\boldsymbol{x})=\sum_n c_n\phi_n(\boldsymbol{x})\tag{1} \end{align}
$c_n$は展開係数であり、一般に複素数です。SEより、個々のエネルギーの固有関数$\phi_n$は以下の時間依存性を持ちます：
\begin{align} \hspace{1.5cm} \exp(-iE_n t/\hbar)\phi_n(\boldsymbol{x}) \end{align}
SEは線形方程式なので、Eq.(1)の時間発展は以下のように与えられます：
\begin{align} \hspace{1.5cm} \psi(\boldsymbol{x},t)=\sum_n c_n \exp(-iE_nt/\hbar)\phi_n(\boldsymbol{x}) \end{align}

ということで、量子系を解く際には、方程式$\hat H\phi_n(\boldsymbol{x})=E_n\phi_n(\boldsymbol{x})$を解いてエネルギーの固有値・固有関数を求めることと、波動関数の初期値をこの固有関数で展開することが主な作業となります。

Bornの規則

ある時刻で波動関数が$\psi=\sum c_n \phi_n$だったとします。ただし$\sum_n|c_n|^2=1$のように規格化されているとします。このとき系のエネルギーを観測すると、$E_m$というエネルギーが確率$|c_m|^2$で得られます。$E_m$を観測したのち、波動関数は$\phi_m$になります。

これはもっと一般に成立します。ある物理量に対応するエルミート演算子$\hat A$の固有状態を$\phi_n^{(A)}$、対応する固有値を$a_n$とします。系の波動関数が$\psi$であるとき、ある$a_m$が観測される確率は、波動関数を$\psi=\sum_n c^{(A)}_n \phi_n^{(A)}$のように展開したときの展開係数により$|c_m^{(A)}|^2$で与えられます（※$\sum_n |c^{(A)}_n|^2=1$のように規格化されているとする）。$a_m$を観測したのち、波動関数は$\phi_m^{(A)}$になります。これをBornの規則と呼びます。

Diracのブラケット表記

以下$|0\rangle,|1\rangle$のような記号が現れます。これはDiracのブラケット表記と呼ばれる量子状態の表示方法です。ここでは$|0\rangle$は基底状態（=いちばんエネルギーの低い状態）$\phi_0$に、$|1\rangle$は第1励起状態（=次にエネルギーの低い状態）$\phi_1$に対応する記号だと思ってください。すなわち$|0\rangle,|1\rangle$はエネルギーの下から2つの状態の基底です。よって
\begin{align} \hspace{1.5cm} \hat H |i\rangle=E_{i}|i\rangle, \ \ \ i=0,1 \end{align}
が成立します。

行列としてのハミルトニアン

量子論では本来Hilbert空間、すなわち無限次元の空間を扱います。しかしながら量子コンピュータでは基本的には有限次元の空間を扱います。いま相互作用を印加する前のハミルトニアン$\hat H_0$の固有状態$|0\rangle,|1\rangle$があるとします。この系に何らかの相互作用$\hat H_I$を印加したとします。全ハミルトニアンを$\hat H =\hat H_0+\hat H_I$とします。このとき
\begin{align} \hspace{1.5cm} \begin{pmatrix} \langle 0|\hat H|0\rangle & \langle 0|\hat H|1\rangle \\ \langle 1|\hat H|0\rangle & \langle 1|\hat H|1\rangle \end{pmatrix} \end{align}
のような行列を作れます。これは$|0\rangle,|1\rangle$をそれぞれ$(1,0)^T,(0,1)^T$に対応させて$\hat H$を表現したものです。全ハミルトニアンのエネルギーの固有値・固有ベクトルを求めることは、この2行2列の行列の固有値・固有ベクトルを求めることに帰着します。

次章以降に現れる行列としてのハミルトニアンはこのようなものです。

量子ゲートで実現したいこと

本記事の「量子ゲートの実装」とは何を実現することなのかについて述べておきます。

2準位系に関し、以下のような任意の状態の表現法があります：
\begin{align} \hspace{1.5cm} |\psi\rangle=\cos\frac{\theta}{2}|0\rangle+e^{i\varphi}\sin\frac{\theta}{2}|1\rangle, \ \ \ 0\le\theta\le\pi,\ 0\le\varphi<2\pi \tag{2} \end{align}
ただしここではoverallの位相ファクターを$|0\rangle$の係数が実になるように固定しています。全体にかかる位相は観測量ではないのでこれで十分です。この状態は$\theta,\ \varphi$を角度として、半径1の球面上の点で表現できます。これをブロッホ球（Bloch sphere）と呼びます（図1）。

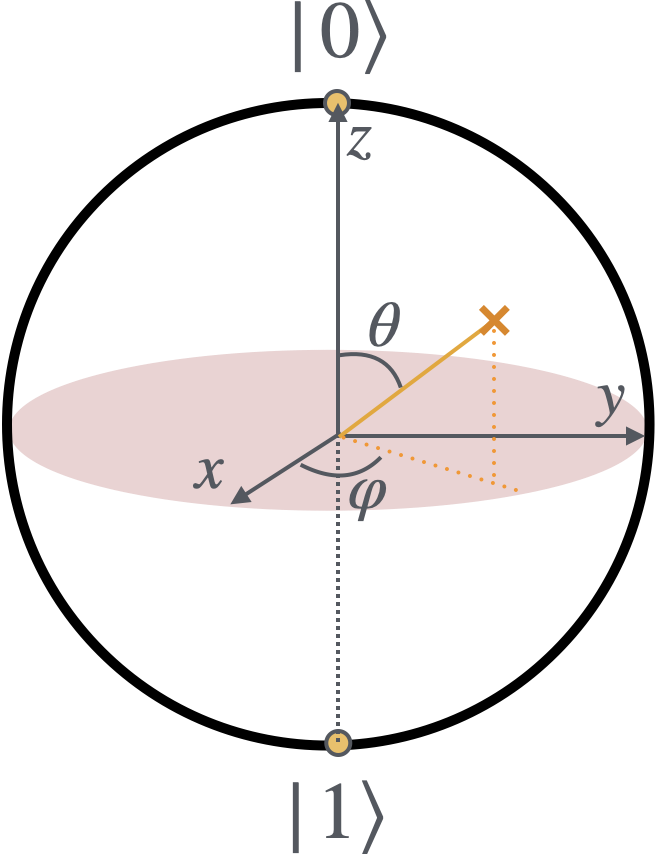ブロッホ球

以下量子ゲートの実装で行うのは、Eq.(2)で表される任意の状態を量子系で実現することです。$\theta,\varphi$を何らかの方法でコントロールできるようにします。これができれば代表的なゲートは以下のように実現できます（量子ゲートに関しては この記事 参照のこと）:

• NOTゲートは$\theta=0\text{ or }\pi,\ \ \varphi=0$
• Hadamardゲートは$\theta=\pi/2,\ \ \varphi=0\text{ or }\pi$
• $R_k$ゲートは$\theta=\pi/2$として$\varphi$を変化させる

ということで、以下Eq.(2)の任意の状態を実現する量子系を構成します。

量子ゲートの実装

本章では量子ゲートの実装の具体例を説明します。

実装その1 : 原子によるラビ振動

以下Ref.Hosoyaに沿って説明します。

$|0\rangle,|1\rangle$の2準位系を考えます。それは例えば原子の2準位系だとしましょう。本来原子の準位はたくさん存在するのですが、ここでは2準位のみが重要な状況を考えます（それが正当化される状況を作る）。

以下のハミルトニアンを考えます：
\begin{align} \hspace{1.5cm} H= \begin{pmatrix} 0 & \lambda e^{i\omega t}\\ \lambda e^{-i\omega t} & \hbar \epsilon \end{pmatrix} \end{align}
ここで$|0\rangle,|1\rangle$を縦ベクトル$(1,0)^T,(0,1)^T$に対応させました。このハミルトニアンは以下のような状況に対応します。基底状態のエネルギーは$0$、第1励起状態のエネルギーは$\hbar \epsilon$の2つの状態があります。これに角振動数$\omega$の光を時間$t$だけ照射します。これにより状態は基底状態と励起状態の間を振動します。これはラビ振動と呼ばれます（コヒーレント振動とも呼ばれます）。以下ラビ振動が起こることを具体的に見ていきます。

注入された光によるラビ振動。$\hbar \omega$のエネルギーをもつ光が系に注入されると、エネルギー差が$\hbar \epsilon$である2準位系のレベル間で振動が起こる

上記ハミルトニアンによる波動関数の時間発展を求めます。このハミルトニアンは時間依存性を持っているので、まずそれを取り除きます。そこで
\begin{align} \hspace{1.5cm} \phi(t):= \begin{pmatrix} a(t) \\ b(t) \end{pmatrix} , \ \ \ \psi(t):= \begin{pmatrix} a(t)\\ e^{-i\omega t}b(t) \end{pmatrix} \end{align}
とします。$\psi(t)$に関するSEは、時間依存性のないハミルトニアン$H_0$を用いて
\begin{align} \hspace{1.5cm} i\hbar\frac{\partial}{\partial t}\phi(t)=H_0\phi(t), \ \ \ H_0:= \begin{pmatrix} 0 & \lambda\\ \lambda & \hbar(\epsilon-\omega) \tag{3} \end{pmatrix} \end{align}
のように書き直せます。$H_0$の固有値$\mu_\pm$、および固有ベクトルは

\begin{align} \hspace{1.5cm} &\text{固有値 : }\mu_\pm=\hbar \frac{(\epsilon-\omega)\pm\sqrt{(\epsilon-\omega)^2+(2\lambda/\hbar)^2}}{2},\\ &\text{固有ベクトル : } \begin{pmatrix} \lambda/\mu_\pm\\ 1 \end{pmatrix} \end{align}

です。

ゆえに$\Phi_\pm :=(\lambda/\mu_\pm, 1)^T$とすると、SEの一般解$\Phi$は、前章の議論より
\begin{align} \hspace{1.5cm} \Phi(t)&=A_+\Phi_+e^{-i\mu_+ t/\hbar}+A_-\Phi_-e^{-i\mu_- t/\hbar},\\ \mu_\pm&=\hbar \frac{(\epsilon-\omega)\pm\sqrt{(\epsilon-\omega)^2+(2\lambda/\hbar)^2}}{2}\tag{4} \end{align}
となります。すなわち角振動数$\omega$の光が系に注入されている間、エネルギー固有値は$\mu_\pm$になり、また波動関数の時間発展はEq.(4)で与えられます。$A_\pm$は波動関数の初期条件と規格化より定まります。

ここで$t=0$で波動関数は基底状態$|0\rangle$にあるとします。すなわち
\begin{align} \hspace{1.5cm} \Phi(t=0)= \begin{pmatrix} 1\\ 0 \end{pmatrix} \end{align}
とします。このとき$A_\pm$はEq.(4)で$t=0$として
\begin{align} \hspace{1.5cm} A_+\Phi_++A_-\Phi_- = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{align}
なので
\begin{align} \hspace{1.5cm} A_+&=-A_-=-\frac{\mu_+\mu_-}{\lambda(\mu_+-\mu_-)}\\ &=\frac{\lambda}{\hbar\sqrt{(\epsilon-\omega)^2+(2\lambda/\hbar)^2}} \end{align}
となります。以上から本セットアップでの波動関数の時間発展は
\begin{align} \hspace{1.5cm} \Phi(t)=\frac{\lambda}{\hbar\sqrt{(\epsilon-\omega)^2+(2\lambda/\hbar)^2}} \left\{ \begin{pmatrix} \lambda/\mu_+\\ 1 \end{pmatrix} e^{-i\mu_+t/\hbar} - \begin{pmatrix} \lambda/\mu_-\\ 1 \end{pmatrix} e^{-i\mu_-t/\hbar} \right\} \end{align}
となります。

ここで相互作用がないときのエネルギー差に等しい振動数$\omega=\epsilon$をもつ光を注入します。このとき$\mu_\pm=\pm \lambda$であり、また
\begin{align} \hspace{1.5cm} \Phi(t)&= \begin{pmatrix} \cos\lambda t \\ -i\sin \lambda t \end{pmatrix} ,\\ \therefore \psi(t)&= \begin{pmatrix} \cos\lambda t \\ -ie^{-i\omega t}\sin \lambda t \end{pmatrix} \end{align}
です。いま$|0\rangle\leftrightarrow(1,0)^T, |1\rangle\leftrightarrow (0,1)^T$に対応させているので、これは
\begin{align} \hspace{1.5cm} \psi(t)\leftrightarrow \cos(\lambda t)|0\rangle-ie^{-i\omega t}\sin(\lambda t)|1\rangle\tag{5} \end{align}
のように書けます。$\lambda,\omega$をうまく調整できれば、$|0\rangle$と$|1\rangle$の相対位相を任意に調整できます。$\omega$は注入する光の角振動数、$\lambda$は光の振幅で調整します。

Eq.(5)はEq.(2)と本質的に同じです。よってラビ振動を用いれば量子ゲートを作ることができます。ただ筆者はこのような量子ゲートが実際にどこまで作成されたか知りません。量子ゲートではなくて恐縮ですが、現実の原子におけるラビ振動として、例えばセシウム原子のラビ振動を電磁波の強度を測定するために応用する研究が存在しますRabi。

その2 : 超伝導量子回路

今度は超伝導体を用いた量子ゲートの実装法を紹介します。最初にも述べたとおり、この方法は実際にGoogleやIBMで使用されている量子コンピュータの実装に用いられていますChoiMukai（※詳細は異なると思います）。この方法が量子ゲートに用いられる理由をRef.Mukaiから引用します：

以下超伝導素子を用いた量子ゲートの実装に関して見ていきます。ここではRef.Mukaiを参考にして、実装の概要を記します。 詳細はRefs.KrantzKockumClarke等をご参照ください。

超伝導体、ジョセフソン電流

超伝導体では電流が無抵抗で流れます。超伝導体を流れる電流はクーパー対 (Cooper pair) と呼ばれる2つの電子が相関した状態が担います。電子2つの組なので、クーパー対の電荷は2eです（電子の電荷をeとする）。

ここで2つの超伝導体の間に薄い絶縁体を挟みます。これをジョセフソン接合（Josephson junction）と呼びます。

ジョセフソン接合。黄色い部分が超伝導体。黒い部分が絶縁体

すると2つの超伝導体の間にジョセフソン電流と呼ばれる電流が流れます。これをジョセフソン効果（Josephson effect）と呼びます。ジョセフソン効果がなぜ起こるかはAppendix 1にゆずります。ここで重要なのは

1. クーパー対が電荷を担う（電荷2e）
2. ジョセフソン電流が流れる

の2つです。これは認めてください。

超伝導量子回路の実装

以下Ref.Mukaiに沿って説明します。図3のような超電導量子回路を考えます。

SQUIDを用いた電荷型の超伝導量子回路

図の黄色の部分は超伝導体です。左右に1つづつジョセフソン接合があります。ジョセフソン接合2つを超伝導体でつないでループにしたデバイスをSQUID（Superconducting Quantum Interference Device）と呼びます。boxと書いてある部分にはクーパー対が溜まります。この箱に貯まるクーパー対の個数の固有状態が本超伝導量子回路における2準位系をなします。$\Phi$はSQUID回路の中を通る磁場を表します。後で述べますが、$\Phi$により2準位間の遷移の周期を調整します。黒い2本線（||の部分）はキャパシタ（コンデンサー）です。$V_g,V_b,V_p$はそれぞれゲート、ベース、プローブにかける電位です。

boxの部分のエネルギー、すなわちそれに対するハミルトニアン$H$は「ジョセフソン電流によるエネルギー+箱に蓄えられたクーパー対の静電エネルギー」で与えられます。電荷による静電エネルギーはコンデンサーと同様で、電荷を$Q$、静電容量を$C$とすると$Q^2/2C$で与えられます。さらにAppendix 1より、ジョセフソン電流によるエネルギーは$-E_J\cos\theta$で与えられます。$\theta$はジョセフソン接合における超伝導体の巨視的波動関数の位相差です。以上からboxにおけるハミルトニアンは
\begin{align} \hspace{1.5cm} H=E_c(n-n_g)^2-E_J \cos \theta \tag{6} \end{align}
で与えられます。$n$は箱の電荷、$n_g$はゲートに溜まる電荷です。ここで$E_c$は熱エネルギー換算で数百mKです。Mukai。よって数十mK程度の低温下では、熱浴によるデコヒーレンスを避けることができます。

系が量子力学で記述される場合、クーパー対が$n$コ存在する量子状態$|n\rangle$で箱の状態を記述できます。ここでは$|0\rangle$がクーパー対0コの状態、$|1\rangle$が1コの状態だと思ってください。$|1\rangle$より上の状態は無視できて、$|0\rangle,|1\rangle$のみで記述できる環境が実現できます。このときEq.(3)の第1項は$|0\rangle,|1\rangle$の固有状態が独立に存在する場合のエネルギー、第2項はその間の遷移を起こす相互作用とみなせます（電流が流れることでクーパー対の個数を変化させる）。そのようなハミルトニアンは

\begin{align} \hspace{1.5cm} H&=\frac{E_c}{2}(n_g-1)\sigma_z+\frac{E_J}{2}\sigma_x\\ &= \begin{pmatrix} \frac{E_c}{2}{(n_g-1)} & E_J/2\\ E_J/2 & -\frac{E_c}{2}{(n_g-1)} \end{pmatrix} \end{align}

のように書くことができます。これは$|0\rangle\leftrightarrow (0,1)^T, \ |1\rangle\leftrightarrow (1,0)^T$と対応させ、また$|0\rangle,|1\rangle$のエネルギーの基準を適切にずらせば（$-E_c(n_g-1)/2$をゼロとする）、Eq.(2)のハミルトニアン$H_0$と同じ形をしています。ゆえにジョセフソン電流が流れると$|0\rangle,|1\rangle$の間でラビ振動を起こし、それらの相対位相を任意にコントロールすることができます。

Eq.(2)の$\lambda$にあたる$E_J$を調整することで$|0\rangle,|1\rangle$の間を振動する周期を調整できます。これはSQUIDに通す外部磁束によってコントロールできます。SQUIDの超伝導体中のクーパー対を記述する波動関数の位相は、SQUIDを一周したとき、波動関数が安定的に存在するために$\text{mod } 2\pi$で元に戻らなければなりません。またAharonov-Bohm効果より、一周したときの波動関数の位相差は、SQUID内に外場として加えた磁場$\Phi_\text{ext}$に依存します。ジョセフソン接合部分での波動関数の位相差$\theta$は、波動関数がSQUIDを一周して$\text{mod } 2\pi$で元に戻る条件より、$\Phi_\text{ext}$に依存して変化します。これは$E_J$を変化させるのと同様の効果を生みます。具体的には$E_J$は$\cos(\pi\Phi_\text{ext}/\Phi_0)$のような依存性を持ちますMukaiKrantzKockum。SQUIDおよびAharonov-Bohm効果に関してはAppendix 2をご参照ください。

このようにして超伝導量子回路で量子ゲートを作成することができます。

シリーズ全体のまとめ

今回が「量子コンピュータにおける素因数分解」の最終回なので、全体の総括をしておきます。

量子コンピュータで最も有名であろうアルゴリズム「Shorのアルゴリズム」に関して説明してきました。このアルゴリズムで重要な量子回路は、べき剰余を計算する回路：
\begin{align} \hspace{1.5cm} a^x\text{ mod }N \ (a,x\text{はゼロ以上の整数,} N\text{は正の整数. } 0\le a< N) \end{align}
および量子フーリエ変換:
\begin{align} \hspace{1.5cm} |j\rangle\to \frac{1}{2^{n/2}} \sum_{k=0}^{2^n-1}\exp(2\pi ijk/2^n)|k\rangle, \ \ \ n\in \mathbb{N}, \ \end{align}
を行う回路です。これら回路を用いて
\begin{align} \hspace{1.5cm} x^r\equiv 1 \text{ mod }N \end{align}
を満たす$r$を見つけます。この$r$が偶数かつ「適切」であれば、$\mathrm{gcd}(x^{r/2}\pm 1,N)$を古典コンピュータで計算することにより$N$の因数を見つけることができます。量子回路による計算量、古典コンピュータによる計算量、および試行錯誤が必要な確率的要素を加味しても、$\log_2 N$の多項式程度の計算量で因数分解を行うことができます。現在まで、古典コンピュータではこのような高速なアルゴリズムは発見されていません。

上記量子回路で用いられている基本的な量子ゲートの実装方法に関しては、本記事で説明したように、いまのところ超伝導量子回路を用いた方法が主流です。クーパー対が0または1コの量子状態間の遷移をSQUIDで調整することにより、任意の1 qubitの状態を実現することができます。

現在のところ、Shorのアルゴリズムによる素因数分解は2桁程度の整数に留まっているようです。現在最も安全な暗号化技術のひとつである、素因数分解の擬似非可逆性を用いたRSA暗号を破るのに有用な桁数の素因数分解はまだまだ先のようです。しかしながら、Shorのアルゴリズムはその古典計算機に対する本質的な優位性、暗号解読という非常に重要な分野への応用、また様々な量子アルゴリズム開発の指針となるような発想を与えたという意味で、理論的なレベルでも十分価値のあるものだと思います。

おしまい。${}_\blacksquare$

Appendix 1 : ジョセフソン効果

本章では超伝導量子回路において基本的な現象であるジョセフソン効果について述べます。特にジョセフソン電流がどうして流れるか、またジョセフソン電流によるエネルギーであるジョセフソンエネルギーについて述べます。参考文献としてRefs.NiwaWikiJosTsunetoを挙げておきます。

ジョセフソン電流

以下Ref.Niwaに沿って説明します。

超伝導体は1つの巨大な（人間のスケールからすると小さいですが）波動関数$\psi(r,t)$で記述できます。ただし2つの超伝導体ではその位相が異なるとしましょう。いま空間1次元で考えます。2つの超伝導体を1,2とラベルし、それぞれの波動関数を$\psi_1(r,t),\psi_2(r,t)$として、さらにこれらを極座標で表示します：
\begin{align} \hspace{1.5cm} \psi_1(r,t)&=|\psi_1(r,t)|\exp(i\phi_1(r,t)),\\ \psi_2(r,t)&=|\psi_2(r,t)|\exp(i\phi_2(r,t)) \end{align}
これらの波動関数はクーパー対に対する波動関数です。

この系のシュレーディンガー方程式がどうなるか考えます。いま2つの超伝導体は薄い絶縁体により弱く結合しています。全系のハミルトニアンは
\begin{align} \hspace{1.5cm} \psi(r,t)=c_1\psi_1(r,t)+c_2\psi_2(r,t) \end{align}
のように書かれます。全形のハミルトニアンは
\begin{align} \hspace{1.5cm} \hat H=\hat H_1+\hat H_2+\hat H_T \end{align}
のように書かれます。ここで$\hat H_1,\hat H_2$はそれぞれ超伝導体1,2が孤立している場合のハミルトニアン、$\hat H_T$はそれらが弱く結合させるハミルトニアンです。いま両方の超伝導体の間に時間に依存しない電圧$V$を印加したとします。$\hat H_1,\hat H_2$のそれぞれのエネルギー固有値を$E_1,E_2$として、接合の両端における$E_1,E_2$の差は
\begin{align} \hspace{1.5cm} E_1-E_2=2eV \end{align}
となります。2eはクーパー対の電荷です。いまエネルギーの原点を$|E_1-E_2|/2$のようにエネルギー差の半分のところにとれば、エネルギーの固有値方程式:$\hat H\psi=E\psi$はそれぞれの超伝導体で
\begin{align} \hspace{1.5cm} \hat H_1\psi_1(r,t)=-eV\psi_1(r,t), \ \ \ \hat H_2\psi_2(r,t)=eV\psi_2(r,t) \end{align}
となります。さらに$\hat H_T$に対する仮定として、$l=1,2$に対するシュレーディンガー方程式に対し、$\hat H_T\psi_{l}(r,t)$を$K\psi_{\bar l}(r,t)$に置き換えます。ただし$l=1,2$に対しそれぞれ$\bar l=2,1$とします。すなわち$1,2$の超伝導体に関する波動関数に対するSEを作るときには、物理系のセットアップから定まるある$K$という定数を「相手の波動関数」にかけた相互作用ハミルトニアンが加わるとします。すると
\begin{align} \hspace{1.5cm} i\hbar\dot\psi_1(r,t)&=-eV\psi_1(r,t)+K\psi_2(r,t)\\ i\hbar\dot\psi_2(r,t)&=eV\psi_2(r,t)+K\psi_1(r,t) \end{align}
が成立します。ここでドットは時間による偏微分です。

このSEに極座標に分解した$\psi_1,\psi_2$を入れて解きます。位相差を$\Delta\phi(r,t):=\phi_2(r,t)-\phi_1(r,t)$とします。上記SEを実部と虚部に分けたうち、虚部のほうをみると
\begin{align} \hspace{1.5cm} 2e\frac{\partial |\psi_1(r,t)|^2}{\partial t}&=\frac{2e}{\hbar}K|\psi_1(r,t)||\psi_2(r,t)|\sin(\Delta \phi(r,t)),\\ 2e\frac{\partial |\psi_2(r,t)|^2}{\partial t}&=-\frac{2e}{\hbar}K|\psi_1(r,t)||\psi_2(r,t)|\sin(\Delta \phi(r,t)) \end{align}
を得ます。ここでも2eはクーパー対の電荷です。クーパー対がこの2つの超伝導体の間を移動すると電流が流れますが、このときの電流は、面積$S$の接合面を流れるとすれば
\begin{align} \hspace{1.5cm} I&=2eS\frac{\partial|\psi_1(r,t)|^2}{\partial t}=-2eS\frac{\partial|\psi_2(r,t)|^2}{\partial t}\\ &=\frac{2e}{\hbar}KS|\psi_1(r,t)||\psi_2(r,t)|\sin(\Delta \phi(r,t))\tag{A1} \end{align}
となります。

ここで注目すべきは、この方程式は$V$には依存していないことです。すなわち2つの超伝導体に位相差$\Delta\phi$さえ存在していれば電流が流れます。もし超伝導体1,2の初期の位相差が時間・空間に関し一定ならば、$I$は直流電流です。これは直流ジョセフソン効果 (DC Josephson effect) と呼ばれます。ふつう電流と電圧の関係は抵抗を$R$としてオームの法則$V=IR$で記述されますが、ジョセフソン電流に電位差は必要ないし抵抗も関係ありません。

次に実部を解析します。実部の方程式より
\begin{align} \hspace{1.5cm} \frac{\partial \Delta\phi(r,t)}{\partial t}= -\frac{2eV}{\hbar}+ \left( \frac{|\psi_2(r,t)|^2-|\psi_1(r,t)|^2}{|\psi_1(r,t)||\psi_2(r,t)|} \right)\frac{K}{\hbar}\cos(\Delta\phi(r,t)) \end{align}
を得ます。1,2の超伝導体は同素材で、位相だけが異なるとすれば$|\psi_1(r,t)|^2=|\psi_2(r,t)|^2$が成立します。このとき上の式の右辺第2項は消えて
\begin{align} \hspace{1.5cm} \frac{\partial \Delta\phi(r,t)}{\partial t}= -\frac{2eV}{\hbar} \tag{A2} \end{align}
と非常に簡単になります。これより電圧$V$が印加された場合、$\Delta\phi(r,t)$は時間$t$に関して線形の依存性をもつことがわかります：
\begin{align} \hspace{1.5cm} \Delta\phi(r,t)=\Delta\phi(r,t=0)-\frac{2eV}{\hbar}t \end{align}
これとEq.(1)より、電圧が印加された場合は周期$\omega=2eV/\hbar$の交流電流が流れることがわかります。これを交流ジョセフソン効果 (AC Josephson effect) とよび、またこの周期をジョセフソン周波数 (Josephson frequency) と呼びます。

ジョセフソン効果は、超伝導の微視的理論であるBCS理論からも、また対称性の自発的破れが生じた際に現れる秩序変数に関する一般論であるGinzburg-Landau理論からも導出できますNiwa。

ジョセフソンエネルギー

ここではジョセフソン電流によるエネルギーを計算します。これはジョセフソン接合における位相差が$0$から$\Delta\phi$まで変化した際に流れるジョセフソン電流のエネルギーです。Ref.WikiJosを参考にしています。

位相差を$\Phi$として、Eq.(A1)を
\begin{align} \hspace{1.5cm} I=I_c \sin\Phi \end{align}
と書いておきます。またEq.(A2)より
\begin{align} \hspace{1.5cm} V=\frac{\hbar}{2e}\frac{\partial \Phi}{\partial t} \end{align}
です。$\Phi$が時刻$t=0$で$0$、$t$で$\Phi=\Delta\phi$とします。この間に流れたジョセフソン電流によるエネルギーは
\begin{align} \hspace{1.5cm} E=\int_0^t IV dt =\int_0^{\Delta\phi}I_c\sin\Phi \ d\left(\frac{2e}{\hbar}\Phi\right) =-\frac{2eI_c}{\hbar}\left[\cos\Phi\right]_0^{\Delta\phi} \end{align}
以上より
\begin{align} \hspace{1.5cm} E(\Delta\phi)=E_J(1-\cos\Delta\phi),\ \ \ E_J=\frac{2eI_c}{\hbar} \end{align}
を得ます。

Appendix 2 : SQUIDとAharonov-Bohm (AB) 効果

SQUIDとは超伝導量子干渉計（Superconducting Quantum Interference Device）の略です。本文図3にあるように、超伝導ループの中に2つのジョセフソン接合を持つデバイスです。通常極めて弱い磁場の検出に用いられる磁気センサーとして用いられますがWiki、本文で述べたように、量子コンピュータでは基底状態と励起状態の振動周期の調整に用いられます。

ここではなぜSQUIDに通す磁場によりその中を流れる電流を制御できるかについて説明します。これはAharonov-Bohm効果と関係します。

Aharonov-Bohm効果

以下Ref.Igiに沿って議論します。Ref.Wachterも参考文献として挙げておきます。

電荷$e$の粒子の波動関数を$\psi$とします。電場・磁場があるとき、SEは以下のようになります：
\begin{align} \hspace{1.5cm} i\hbar\frac{\partial\psi}{\partial t} = \left\{ -\frac{\hbar^2}{2m}\left(\frac{\partial}{\partial{\boldsymbol x}}-\frac{ie}{\hbar c}\boldsymbol{A}\right)^2+e\phi \right\}\psi\tag{A3} \end{align}

ここで$\boldsymbol{A},\phi$はそれぞれベクトルポテンシャル、スカラーポテンシャルと呼ばれます。これらの量を組にして$A_\mu=(\phi,{\boldsymbol A})$のように4次元のベクトルとしたものはゲージ場と呼ばれます。ゲージ場と電場$\boldsymbol{E}$と磁場$\boldsymbol{B}$との関係は以下です：

\begin{align} \hspace{1.5cm} \boldsymbol{E}=-\grad\phi +\frac{1}{c}\frac{\partial \boldsymbol{A}}{\partial t}, \ \ \ \boldsymbol{B}=\text{rot}\boldsymbol{A} \tag{A4} \end{align}

Eq.(A3)は$\chi(\boldsymbol{x},t)$を場所・時刻に依存する任意の関数として

\begin{align} \hspace{1.5cm} \boldsymbol{A}\to \boldsymbol{A}-\grad \chi, \ \ \ \phi\to\phi+\frac{1}{c}\frac{\partial}{\partial t}\chi, \ \ \ \psi\to \exp\left[-i\frac{e}{\hbar c}\chi\right]\psi \end{align}

に対して不変です。この変換をゲージ変換、この変換に対して不変なことをゲージ不変性、$\chi$をゲージ関数と呼びます。観測可能な量はすべてゲージ不変です。電場・磁場は観測可能なのでゲージ不変です。「物理量はゲージ不変であれ」という原理はゲージ原理と呼ばれます。ゲージ原理を指針として、SEのゲージ不変性を要請することでEq.(A3)を導くこともできます。$\boldsymbol{A},\phi$を結合させ、かつゲージ不変にするには、時間および空間微分を

\begin{align} \hspace{1.5cm} \frac{\hbar}{i}\frac{\partial}{\partial{\boldsymbol x}}\to \frac{\hbar}{i}\frac{\partial}{\partial{\boldsymbol x}}-\frac{e}{c}\boldsymbol{A}, \ \ \ i\hbar\frac{\partial}{\partial t}\to i\hbar\frac{\partial}{\partial t}-e\phi \end{align}
のように置き換えればよいことが知られています。このようにゲージ場と粒子との結合を得る方法はminimal couplingなどと呼ばれます。

ここで重要なのは、量子論においては電場・磁場ではなくゲージ場が本質的に現れることです。局所的な場の理論では電場・磁場のみで運動方程式を書くことは不可能です。

量子論におけるゲージ場の重要性が如実に現れるのがAharanov-Bohm効果です。いま電場は無視して$\phi=0$とします。Eq.(A3)で$\phi=0$とした方程式

\begin{align} \hspace{1.5cm} i\hbar\frac{\partial\psi}{\partial t} = -\frac{\hbar^2}{2m}\left(\frac{\partial}{\partial{\boldsymbol x}}-\frac{ie}{\hbar c}\boldsymbol{A}\right)^2\psi\tag{A5} \end{align}

となりますが、ここで$\psi$を

\begin{align} \hspace{1.5cm} \psi=\exp\left[i\frac{e}{\hbar c}\chi\right]\psi' \tag{A6} \end{align}

とします。ここで$\chi$は$\boldsymbol{A}=\grad\chi$を満たす関数とします。このとき$\boldsymbol{B}=\text{rot}\boldsymbol{A}=\grad\times\boldsymbol{A}$はゼロです。これは直接計算でももちろんわかりますが、次のような考察からもわかります：$\boldsymbol{A}=\grad\chi$は$\boldsymbol{A}=\boldsymbol{0}$からゲージ関数$\chi$によるゲージ変換をしたベクトルポテンシャルですが、$\boldsymbol{A}=\boldsymbol{0}$で磁場がゼロなのは明らかなので、$\boldsymbol{A}=\grad\chi$による磁場もそのゲージ不変性からゼロになります。

$\psi'$でEq.(A5)を書き直すと

\begin{align} \hspace{1.5cm} i\hbar\frac{\partial}{\partial t}\psi'=-\frac{\hbar^2}{2m}\grad^2\psi' \end{align}

となります。すなわち$\boldsymbol{A}$がノンゼロでも、それが与える$\boldsymbol{B}$がゼロならば、$\psi'$は自由なSEに従います。波動関数のoverallな位相は物理的ではないので、結局この状況では粒子は自由運動をすることがわかります。

さて、$\boldsymbol{A}=\grad \chi$を満たす$\chi$は線積分を用いて
\begin{align} \hspace{1.5cm} \chi(\boldsymbol{x})=\int_{\cal{C}\ \boldsymbol{x}_0}^{\boldsymbol{x}} {\boldsymbol{A}(\boldsymbol{x}')}\cdot d\boldsymbol{x}' \ \ \ \ (\cal{C}\text{は粒子の経路}) \tag{A7} \end{align}
と書けることは、これを$\boldsymbol{A}=\grad \chi$に代入すればすぐにわかります。Eq.(A7)とEq.(A6)と合わせると、ベクトルポテンシャルの存在の元で運動する粒子には、その粒子の軌道上に存在するベクトルポテンシャル$\boldsymbol{A}(\boldsymbol{x})$に依存した位相がかかることがわかります。

上記したように位相そのものは観測量ではありません。しかし位相差は観測にかかる場合があります。ゲージ場が波動関数に及ぼす影響を見るために、以下の図のような2重スリットの状況を考えます。

磁場の存在する2重スリット実験。荷電粒子（電荷$e$）が$\boldsymbol{x}_0$から$\boldsymbol{x}$に到達する様子。$C_A,C_B$はそれぞれスリットA,Bを通る場合の到達経路

ゲージ場が存在しない場合、経路$A,B$を通り$\boldsymbol{x}_0$から$\boldsymbol{x}$まで移動した粒子の$\boldsymbol{x}$における波動関数をそれぞれ$\psi^{A,B}_\text{free}(\boldsymbol{x})$とします。一方ゲージ場が存在する場合の同様の波動関数をそれぞれ$\psi^{A,B}_{g}(\boldsymbol{x})$とします。するとEq.(A6)(A7)より

\begin{align} \hspace{1.5cm} \psi_g^A(\boldsymbol{x})=\exp\left[i\frac{e}{\hbar c}\int_{\cal{C}_A \ \boldsymbol{x}_0}^{\boldsymbol{x}}{\boldsymbol{A}}(\boldsymbol{x}')\cdot d\boldsymbol{x}'\right]\psi^{A}_\text{free}, \ \ \ \psi_g^B(\boldsymbol{x})=\exp\left[i\frac{e}{\hbar c}\int_{\cal{C}_B \ \boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}'\right]\psi^{B}_\text{free} \end{align}

となります。よってゲージ場が存在する下で、$\boldsymbol{x}$における波動関数は、経路$A,B$を通った波動関数の和になるので

\begin{align} \hspace{1.5cm} \psi_\text{tot}(\boldsymbol{x})&=\psi_g^A(\boldsymbol{x})+\psi_g^B(\boldsymbol{x})\\ &=\exp\left[i\frac{e}{\hbar c}\int_{\cal{C}_A \ \boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}'\right] \left\{ \psi_\text{free}^A(\boldsymbol{x})+ \exp\left[i\frac{e}{\hbar c} \left( \int_{\cal{C}_B \ \boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}' - \int_{\cal{C}_A \ \boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}' \right) \right]\psi_\text{free}^B(\boldsymbol{x}) \right\}\\ &=\exp\left[i\frac{e}{\hbar c}\int_{\cal{C}_A \ \boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}'\right] \left\{ \psi_\text{free}^A(\boldsymbol{x})+ \exp\left[i\frac{e}{\hbar c} \int_{\cal{C}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}' \right]\psi_\text{free}^B(\boldsymbol{x}) \right\} \end{align}

となります。ここで$\cal{C}=\cal{C}_B-\cal{C}_A$です。ストークスの定理を用いれば

\begin{align} \hspace{1.5cm} \int_{\cal{C}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}' &=\int_S \text{rot} \boldsymbol{A}\cdot d\boldsymbol{S}\\ &=\int_S \boldsymbol{B}\cdot d\boldsymbol{S}\tag{A8}\\ &=:\Phi \end{align}

となります。ここで$S$は$C$を境界とする2次元面です。$\Phi$は$S$を貫く磁束です。よって、粒子が$ \boldsymbol{x}_0$から${\boldsymbol{x}}$に到達する確率は、その経路を境界とする2次元面を通る磁場により変化します。Eq.(A8)はゲージ変換$\boldsymbol{A}\to \boldsymbol{A}-\grad \chi$で不変であることに注意してください。

粒子が$C_A$または$C_B$を通り$\boldsymbol{x}_0$から$\boldsymbol{x}$に至る確率密度は$|\psi_\text{tot}|^2$です。軌道$C$の中に磁場がなければ

\begin{align} \hspace{1.5cm} |\psi_\text{tot}|^2=|\psi^A_\text{free}+\psi^B_\text{free}|^2 \end{align}

です。一方$C$内に磁場が存在すれば

\begin{align} \hspace{1.5cm} |\psi_\text{tot}|^2 &= \left| \psi_\text{free}^A(\boldsymbol{x})+ \exp\left[i\frac{e}{\hbar c} \int_{\cal{C}}\boldsymbol{A}(\boldsymbol{x}')\cdot d\boldsymbol{x}' \right]\psi_\text{free}^B(\boldsymbol{x}) \right|^2\\ &=|\psi_\text{free}^A|^2+|\psi_\text{free}^B|^2 +(\psi_\text{free}^A)^*\exp\left[i\frac{e\Phi}{\hbar c}\right]\psi_\text{free}^B(\boldsymbol{x}) +\psi_\text{free}^A\left(\exp\left[i\frac{e\Phi}{\hbar c}\right]\psi_\text{free}^B(\boldsymbol{x})\right)^* \end{align}

となります。最後の2項が$S$を貫く磁束$\Phi$に依存します。よって$\boldsymbol{x}$に粒子が至る確率も$\Phi$に依存します。これがAharanov-Bohm（AB）効果です。上記したようにAB効果はゲージ不変な現象です。

超伝導ループとSQUID

ここまでは電子を2重スリットに通す場合を考えましたが、同様なことを超伝導体のループにあてはめます。超伝導体は1つの巨視的な（クーパー対を記述する）波動関数で表せます。波動関数が安定して存在するには、それが超伝導体を一周すると元に戻らなければなりません。ところが磁場をループ内に通すと、波動関数が一周する間にAB効果により波動関数に$2e\Phi/\hbar c$という余計な位相がつきます。Bohr-Sommerfeldの量子化条件と同様、超伝導体内を一周した波動関数が元に戻る条件:

\begin{align} \hspace{1.5cm} \frac{2e\Phi}{\hbar c} =2n\pi,\ n\in \mathbb{Z} \end{align}

を満たす必要があります。$S$は超伝導体ループを境界とする2次元面です。このように超伝導体ループではループを貫く磁場は離散化された値を取ります。いわゆる磁束の量子化が起こります。

SQUIDでは超伝導体ループの途中に存在するジョセフソン接合にさらに位相差$\theta$が存在するので
\begin{align} \hspace{1.5cm} \theta +\frac{2e\Phi}{\hbar c}=2n\pi, \ \ \ n\in \mathbb{Z} \end{align}

が成立します。故に超伝導体の位相差$\theta$を外部からSQUIDにかける磁束$\Phi$により調節できます。これによりジョセフソン電流は$\Phi$の依存性をもち、ひいてはEq.(8)の$E_J$は（有効的に）$\Phi$により変化します。

余談ですが、Aharanov-Bohm効果は、その存在を多くの物理学者が認めるまでに理論的提案から30年ほどかかりました。その間に幾多の反論を受けました。AB効果の存在を示す決定的な実験が日立の基礎研において行われたことは有名です。それに至るまでの経緯およびその実験に関しては外村彰さんの書かれたRef.Tonomuraがわかりやすいです。なぜAB効果に関してそれほど批判があり認め難いのかに関してもこの論文を読まれるとよいと思います。