Odd-Even Topology を紹介したいと思います

位相空間論

213

どうも

　今回は位相空間の具体例、Odd-Even Topology を紹介します。位相空間初心者の方でも読めます！！！
　個人的に好きな位相空間なのですが、そこまでは有名ではない気がするのでこの記事で紹介したいと思います。

早速定義します

　位相空間のもとになる集合は自然数の全体$\mathbb{N} = \{1,2,3, \cdots\}$になります。まあこの記事では$0$を含めないことにします。

　さてさて開集合を定義しましょう。Odd-Even Topology の開集合は、その名の通り偶奇にまつわるものです。その構成方法ですが、$\{1,2\},\{3,4\},\{5,6\},\cdots$ のような、$\{2n-1,2n\}$の形の集合を開集合とするというものです。（位相空間に慣れている人は、これが開基になっている、ということで納得して下さい。以下慣れていない人向けの説明です）

どういう開集合があるのか

　$\{2n-1,2n\}$の形の集合を開集合とする、と書きましたが、これでは少し言葉が足りません。開集合の和集合はまた開集合である必要があるので、$\{1,2\},\{3,4\}$が開集合であるなら$\{1,2,3,4\}$も開集合である必要があります。あとは空集合も開集合である必要がありますね。

　なので実際は、$\{2n-1,2n\}$の形の元の和集合たちすべてと空集合を開集合としています。この開集合たちで位相空間となります。（証明略）

アイキャッチ

空間としての性質は？

　位相空間に慣れた人向けに書いてしまうと、

・第1可算公理、第2可算公理を満たす
・リンデレフ空間でありコンパクトでない
・局所コンパクトである
・ハウスドルフでない
・連結でない
・局所連結である

　といった感じです。この記事ではこれとは関係なく、これがどういう空間であるのかの直感を与えることを目的とします。

離散位相と密着位相を復習

　私が書いた離散位相と密着位相を説明した記事（これです）を読んでいただけたらそれで良いのですが、ここでも軽く説明します。

　今回の記事で考えるのは$2$点集合の場合なので、その場合のみを説明します。

　集合$X=\{1,2\}$を考える場合だと、その開集合が$\emptyset,\{1\},\{2\},X$であるものが離散位相です。点$x=1$のまわりの近傍を考えると、近傍$\{1\}$が取れます。自分しか含まない近傍が取れるということは、$1$から見た他の点はすべて離れているということです。つまり離散的ですね！

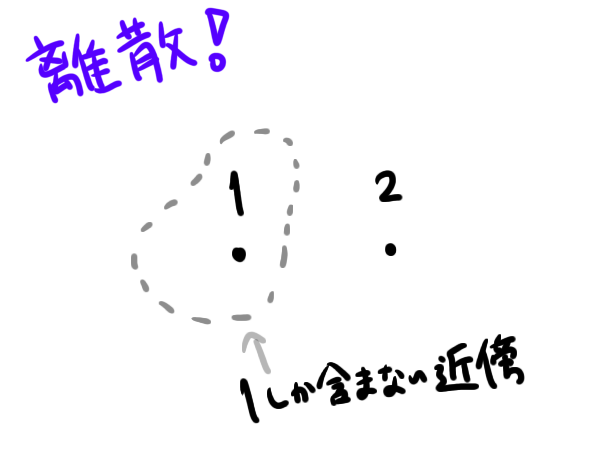離散位相の図

　集合$X=\{1,2\}$を考える場合だと、その開集合が$\emptyset$と$X$のみであるものが密着位相です。点$x=1$のまわりの近傍を考えると、$x$を含む開集合が$X=\{1,2\}$しかないので、近傍$N$を取ると絶対に$2 \in N$となってしまいます。点$x=1$の近傍を取ると必ず$2$が入ってしまうということは、$1$から見た$2$はこれ以上無いくらい、非常に近い位置にあるといえます。つまり密着していますね！

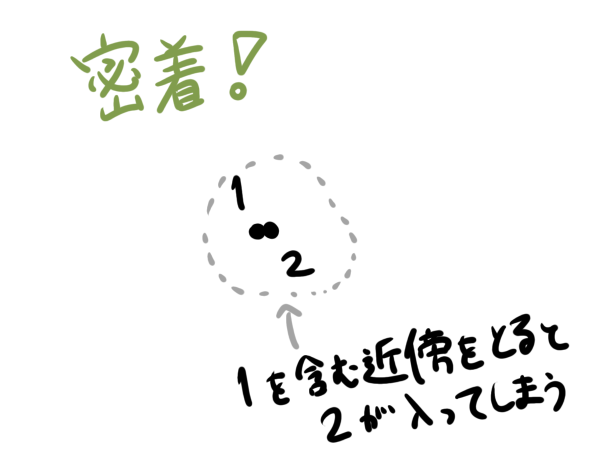密着位相の図

相対位相を復習

　私が書いた相対位相を説明した記事（これです）を読んでいただけたらそれで良いのですが、ここでも軽く説明します。

　相対位相というのは、位相空間の部分集合からすこし小さい位相空間を作ったものです。
　位相空間$X$の部分集合$A$に対して、$A$の開集合を$\{O \cap A$$|$$ O$は$X$の開集合$\}$で定めると、これは位相空間となります。これを$A$による相対位相とか言います。

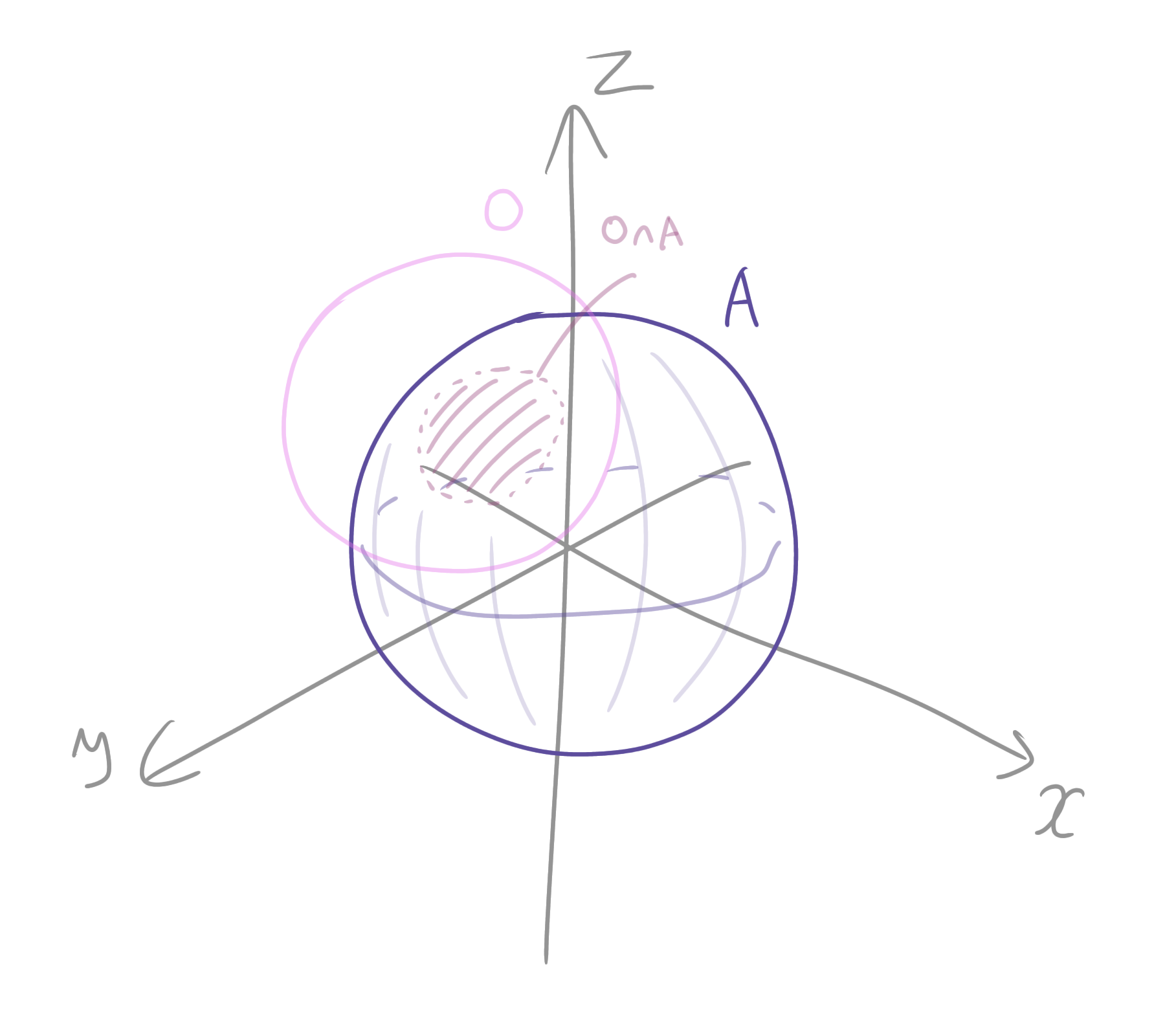相対位相の図

本題に戻ります

　ではではこの Odd-Even Topology なのですが、$A=\{1,2\}$として、この$A$による相対位相を考えます。$A$と共通部分をもつ開集合ですが、それはすべて$\{1,2\}$を含んでいるはずです。なぜなら Odd-Even Topology の開集合は、$\{2n-1,2n\}$の形の元の和集合であったからです。

　ということは、$A$による相対位相の開集合は$\emptyset, A=\{1,2\}$のみになります。ん？これは密着位相ですね。つまり$1,2$は密着しています。

　同様に、$\{3,4\}$や$\{9,10\}$で相対位相を考えても密着位相になります。つまり、点$2n-1, 2n$は密着しています。

　では今度は$B=\{2,3\}$としましょう。$B$による相対位相の開集合は$\emptyset,\{2\},\{3\},B$として取れます。こちらは離散位相ですね。

　同様に、$2n-1, 2n$の組でなければ、$2$点で考えた相対位相は離散位相になります。
　これらを踏まえた図を考えると、次のようになる.......と私はイメージしています。

ちょっとキモい図かも

成り立つことを一つ書いて終わりにします

　上の議論から、点$1,2$は密着しているので、例えば次のような命題が成立します。

こんな数列が収束する

　Odd-Even Topology において、点列$\{a_n\}$が$a_i \in \{1,2\}$を満たしているなら、これは点$1$と点$2$に収束する。

　（収束の定義を貼っておきます。）

点列の収束

　$(X,\mathcal{O})$を位相空間とする. 点列$\{x_n\}_{n\in\mathbb{N}}$が点$x \in X$に収束する（$x$が点列の極限値）とは, 次を満たすことである.
　・任意の点$x$の近傍$N \subset X$に対し$n_0 \in \mathbb{N}$が存在して, $n > n_0$となる任意の$n \in \mathbb{N}$について$x_n \in N$が成立する.