Proposition1~15の解説

\begin{eqnarray} \int_0^1\frac{\ln(1+x+x^2)}{x}dx&=&\int_0^1\frac{\ln(1-x^3)-\ln(1-x)}{x}dx\\ &=&\frac{1}{3}\int_0^1\frac{\ln(1-t)}{t}dt-\int_0^1\frac{\ln(1-x)}{x}dx \ \ (x^3\to t)\\ &=&-\frac{2}{3}\int_0^1\frac{\ln(1-x)}{x}dx\\ &=&\frac{2}{3}\zeta(2)=\frac{\pi^2}{9} \end{eqnarray}

先ず,次が成り立つ.
\begin{align} \int_{-\infty}^\infty\frac{e^{zx}}{\cosh^sx}dx=2^{s-1}\frac{\Gamma(\frac{s+z}{2})\Gamma(\frac{s-z}{2})}{\Gamma(s)} \end{align}
次に,$x\in(0,\infty)$で$\frac{1}{\cosh x}\lt1$であるから次が成り立つ
\begin{eqnarray} \int_{-\infty}^{\infty}e^{aix}\ln\left(\frac{1}{1-\frac{1}{\cosh^2 x}}\right)dx=\sum_{n\geq0}\frac{1}{n+1}\int_{-\infty}^\infty\frac{e^{aix}}{\cosh^{2n+2}x}dx \end{eqnarray}
先程の式において$z=ai,s=2n+2$として和を取る.
途中 Clausen's formula を用いる.
\begin{eqnarray} \sum_{n\geq0}\frac{1}{n+1}\int_{-\infty}^{\infty}\frac{e^{aix}}{\cosh^{2n+2}x}dx&=&2\Gamma\left(1+\frac{ai}{2}\right)\Gamma\left(1-\frac{ai}{2}\right)\ _3F_2\left[\begin{matrix}1,1+\frac{ai}{2},1-\frac{ai}{2}\\2,\frac{3}{2}\end{matrix};1\right]\\ &=&2\Gamma\left(1+\frac{ai}{2}\right)\Gamma\left(1-\frac{ai}{2}\right)\ _2F_1\left[\begin{matrix}\frac{1}{2}+\frac{ai}{4},\frac{1}{2}-\frac{ai}{4}\\\frac{3}{2} \end{matrix};1\right]^2\ \ (\because Clausen's\ \ formula)\\ &=&2\Gamma\left(1+\frac{ai}{2}\right)\Gamma\left(1-\frac{ai}{2}\right) \left(\frac{\Gamma(\frac{3}{2})\Gamma(\frac{1}{2})}{\Gamma(1-\frac{ai}{4})\Gamma(1+\frac{ai}{4})}\right)^2\\ &=&\frac{2\pi}{a}\tanh\frac{a\pi}{4} \end{eqnarray}

置換により同型が出現します.
\begin{eqnarray} \int_0^1\frac{\ln(1+x)}{1+x^2}dx&=&\int_0^1\frac{\ln\frac{2}{1+x}}{1+x^2}dx\ \ \ \left(x\to \frac{1-x}{1+x} \right)\\ &=&\frac{\pi}{4}\ln2-\int_0^1\frac{\ln(1+x)}{1+x^2}dx\\ &=&\frac{\pi}{8}\ln2 \end{eqnarray}

先ず,
\begin{eqnarray} \int_0^{\pi/2}\ln\left(1+a\sin x\right)dx=\int_0^{\pi/2}\int_0^a\frac{\sin x}{1+t\sin x}dtdx \end{eqnarray}
がすぐにわかります.次に$\lvert t\lvert\lt1$におけるxでの積分を考えます.
\begin{eqnarray} \int_0^{\pi/2}\frac{\sin x}{1+t\sin x}dx&=&\int_0^{\pi/2}\left(1-\frac{1}{1+t\sin x}\right)\frac{dx}{t}\\ \int_0^{\pi/2}\frac{dx}{1+t\sin x}&=&\int_0^1\frac{2}{1+2tx+x^2}dx \ \ \ \left(\tan\frac{x}{2}\to x\right)\\ &=&\int_0^1\frac{2}{(x+t)^2+1-t^2}dx\\ &=&\frac{2}{\sqrt{1-t^2}}\left(\tan^{-1}\sqrt{\frac{1+t}{1-t}}-\tan^{-1}\frac{t}{\sqrt{1-t^2}}\right)\\ &=&\frac{\pi-\cos^{-1}t-2\sin^{-1}t}{\sqrt{1-t^2}} \end{eqnarray}
これにより,フビニの定理より,$0\leq a\lt1$に対して
\begin{eqnarray} \int_0^{\pi/2}\ln\left(1+a\sin x\right)dx=\int_0^{\sin^{-1}a}\frac{x-\frac{\pi}{2}(1-\cos x)}{\sin x}dx=\int_0^{\sin^{-1}a}\frac{x}{\sin x}dx+\frac{\pi}{2}\ln\frac{1+\sqrt{1-a^2}}{2} \end{eqnarray}
となることがわかります.
次に,最右辺の第一項をprop33を用いて級数展開します.
簡単のため$a\to\sin a$とします.
\begin{eqnarray} \int_0^a\frac{x}{\sin x}dx&=&-\int_0^a\frac{2ix}{1-e^{2ix}}dx\\ &=&-2i\sum_{n\geq0}\int_0^axe^{(2n+1)ix}dx\\ &=&\sum_{n\geq0}\frac{2i}{(2n+1)^2}-\frac{2ae^{(2n+1)ia}}{2n+1}-\frac{2ie^{(2n+1)ia}}{(2n+1)^2}\\ &=&2\sum_{n\geq0}\frac{\sin(2n+1)a}{(2n+1)^2}-\frac{a\cos(2n+1)a}{2n+1}\\ &=&2\sum_{n\geq0}\frac{\sin(2n+1)a}{(2n+1)^2}+a\ln\tan\frac{a}{2} \end{eqnarray}
以上より,
\begin{eqnarray} \int_0^{\pi/2}\ln\left(1+\sin a\sin x\right)dx=2\sum_{n\geq0}\frac{\sin(2n+1)a}{(2n+1)^2}+a\ln\tan\frac{a}{2}+\pi\ln\cos\frac{a}{2} \end{eqnarray}
最後に,$\sin\frac{2n+1}{6}\pi=\frac{(-1)^n+3\delta_{n\equiv1}-3\delta_{n\equiv4}}{2} \mod6$
$(\delta_{n\equiv a}$で$n\equiv a$のとき１,それ以外で０となる関数とする$)$
と表せることから
\begin{eqnarray} \sum_{n\geq0}\frac{\sin\frac{2n+1}{6}\pi}{(2n+1)^2}=\frac{1}{2}\sum_{n\geq0}\frac{(-1)^n}{(2n+1)^2}+\frac{3}{(12n+3)^2}-\frac{3}{(12n+9)^2}=\frac{2}{3}\beta(2) \end{eqnarray}
と計算でき題意が示せました.

\begin{eqnarray} \int_{-\infty}^\infty\frac{e^{zx}}{\cosh^{s}x}dx&=&\int_{-\infty}^{\infty}\frac{2^{s}e^{(z+s)x}}{(1+e^{2x})^s}dx\\ &=&\int_0^{\infty}\frac{2^{s-1}x^{\frac{z+s}{2}-1}}{(1+x)^s}dx \ \ (e^{2x}\to x)\\ &=&2^{s-1}\frac{\Gamma(\frac{s+z}{2})\Gamma(\frac{s-z}{2})}{\Gamma(s)} \end{eqnarray}
最後にベータ関数の積分表示の逆を用いた.
以上より,
\begin{eqnarray} \int_0^{\infty}\frac{\cos 2ax}{\cosh^{2n}x}dx&=&\int_{-\infty}^{\infty}\frac{e^{2aix}}{2\cosh^{2s}x}dx\\ &=&\frac{2^{2n}\Gamma(n-ai)\Gamma(n+ai)}{4\Gamma(2n)}\\ &=&\frac{2^{2n}}{4\Gamma(2n)}\frac{1}{(n^2+a^2)e^{2\gamma n}}\prod_{m\geq1}\left(\frac{1+\frac{a^2}{(n+m)^2}}{\frac{1}{(1+\frac{n}{m})^2}}\right)^{-1}e^{2n/m}\\ &=&\frac{2^{2n}\Gamma(n)^2}{4\Gamma(2n)}\prod_{m\geq0}\left(1+\frac{a^2}{(n+m)^2}\right)^{-1} \end{eqnarray}
となる（途中乗積表示を用いた）

prop10より,
\begin{eqnarray} \int_0^{\pi}\ln\tanh^{-1}\alpha e^{ix}dx=\pi\ln\alpha+\frac{\pi^2i}{2} \end{eqnarray}
偏角を$(-\pi,\pi]$,$\alpha\to1^{-}$とし
\begin{eqnarray} (RHS)&=&\frac{\pi^2i}{2}\\ (LHS)&=&\int_0^{\pi}\ln\left(\frac{1}{2}\ln\frac{1+e^{ix}}{1-e^{ix}}\right)dx\\ &=&-\pi\ln2+2\int_0^{\pi/2}\ln\ln\left(\frac{1+e^{2ix}}{1-e^{2ix}}\frac{i}{i}\right)dx\\ &=&-\pi\ln2+2\int_0^{\pi/2}\ln\left(-\frac{\pi i}{2}-\ln\tan x\right)dx\end{eqnarray}
\begin{eqnarray} \because\int_0^{\pi/2}\ln\left(-\frac{\pi}{2}+i\ln\tan x\right)dx&=&\frac{\pi}{2}\ln2 \end{eqnarray}
実部比較により題意を得る.

\begin{eqnarray} I:&=&\int_0^{\pi/2}\frac{x}{\sin x+\cos x+1}dx\\ &=&\int_0^{\pi/2}\frac{\frac{\pi}{2}}{\sin x+\cos x+1}dx-I\\&=&\frac{\pi}{4}\int_0^{1}\frac{1}{x+1}dx\ \ \ \ \left(\tan\frac{x}{2}\to x\right)\\ &=&\frac{\pi}{4}\ln2 \end{eqnarray}

\begin{eqnarray} I(a):&=&\int_0^\pi\ln\tanh^{-1}a e^{ix}dx\\ \end{eqnarray}
$I(a)$の被積分関数は$0\leq a\leq1$で連続関数となるので以下その範囲のみを考えます.
\begin{eqnarray} \frac{d}{da}I(a)&=&\int_0^{\pi}\frac{\partial}{\partial a}f(a e^{ix})dx\\ &=&\int_0^{\pi}\frac{1}{ai}\frac{\partial}{\partial x}f(ae^{ix})dx\\ &=&\frac{f(-a)-f(a)}{ai}\\ &=&\frac{\ln\frac{\ln\frac{1-a}{1+a}}{\ln\frac{1+a}{1-a}}}{ai}=\frac{\pi}{a} \end{eqnarray}
$\varepsilon\lt\lt1$とする.
\begin{eqnarray} I(a)-I(\varepsilon)&=&\int_{\varepsilon}^{a}\frac{\pi}{x}dx\\ (RHS)&=&\pi\ln a-\pi\ln\varepsilon\\ \end{eqnarray}
次に左辺の$I(\varepsilon)$にピュイズー級数を用います.
\begin{eqnarray} I(\varepsilon)&=&\int_0^{\pi}\ln \varepsilon +ix+\frac{\varepsilon^2e^{2ix}}{3}+O(\varepsilon^4)dx\\ &=&\pi\ln\varepsilon+\frac{\pi^2i}{2} \end{eqnarray}
以上より,
\begin{eqnarray} I(a)&=&I(\varepsilon)-\pi\ln\varepsilon+\pi\ln a\\ &=&\pi\ln a+\frac{\pi^2i}{2}\\ \end{eqnarray}

\begin{eqnarray} \int_0^1x^{2n}K'(x)dx=\frac{\pi^2}{4}\beta_n^2 \end{eqnarray}
を用いる.
\begin{eqnarray} \sum_{n\geq0}\frac{\beta_n^3}{n+1}&=&\frac{4}{\pi^2}\int_0^1\sum_{n\geq0}\frac{\beta_n}{n+1}x^{2n}K'(x)dx\\ &=&\frac{8}{\pi^2}\int_0^1K'(x^2)\frac{dx}{x^2}\int_0^x\sum_{n\geq0}\beta_ny^{2n+1}dy\\ &=&\frac{8}{\pi^2}\int_0^1K'(x)\frac{dx}{x^2}\int_0^x\frac{y}{\sqrt{1-y^2}}dy\\ &=&\frac{8}{\pi^2}\int_0^1\frac{1-\sqrt{1-x^2}}{x^2}K'(x)dx\\ &=&\frac{8}{\pi^2}\int_0^1\frac{K'(x)}{1+\sqrt{1-x^2}}dx \end{eqnarray}
Landen Trasform $\frac{1}{1+x^2}K\left(\frac{2x}{1+x^2}\right)=K(x^2)$に対して$x\to\sqrt{\frac{1-x^2}{1+x^2}}$とすると$\frac{2}{1+x^2}K'(\frac{2x}{1+x^2})=K'(x^2)$がわかります.これを用いてさらに変形していきます.
\begin{eqnarray} (RHS)&=&\frac{8}{\pi^2}\int_0^1(1-x^2)\frac{\frac{2}{1+x^2}K'\left(\frac{2x}{1+x^2}\right)}{1+x^2+(1-x^2)}dx\ \ \ \ \left(x\to\frac{2x}{1+x^2}\right)\\ &=&\frac{4}{\pi^2}\int_0^1(1-x^2)K'(x^2)dx\\ &=&\frac{1}{2\pi}\int_0^1(x^{-\frac{3}{4}}-x^{-\frac{1}{4}})\sum_{n\geq0}\beta_n^2(1-x)^ndx\ \ (x^4\to x) \\ \end{eqnarray}
最後に,
\begin{eqnarray} \int_0^1x^{s-1}\sum_{n\geq0}\beta_n^2(1-x)^ndx&=&\sum_{n\geq0}\frac{(\frac{1}{2})_n^2}{(1)_n^2}\frac{\Gamma(s)\Gamma(n+1)}{\Gamma(n+s+1)}\\ &=&\frac{\Gamma(s)}{\Gamma(\frac{1}{2})\Gamma(s+\frac{1}{2})}\sum_{n\geq0}\frac{(\frac{1}{2})_n}{n!}\int_0^1x^{n-\frac{1}{2}}(1-x)^{s-\frac{1}{2}}dx\\ &=&\frac{\Gamma(s)}{\Gamma(\frac{1}{2})\Gamma(s+\frac{1}{2})}\int_0^1x^{-\frac{1}{2}}(1-x)^{s-1}dx\\ &=&\frac{\Gamma(s)^2}{\Gamma(s+\frac{1}{2})^2} \end{eqnarray}
なので
\begin{eqnarray} \sum_{n\geq0}\frac{\beta_n^3}{n+1}&=&\frac{1}{2\pi}\left(\frac{2\pi^2}{\Gamma(\frac{3}{4})^4}-\frac{8\Gamma(\frac{3}{4})^4}{\pi^2}\right)\\ &=&A-\frac{4}{\pi^2}A^{-1} \end{eqnarray}
となります.

先程の式の両辺に$a^{s-1}$をかけ$a\in[0,\infty)$で積分します.
\begin{eqnarray} \mathrm{Im}\int_0^{\infty}a^{s-1}\int_0^{1}e^{-a\sqrt{x}(\kappa(x)-i\kappa(1-x))}\frac{dxda}{1-xt}=\frac{\pi}{t}\int_0^{\infty}a^{s-1}(e^{-a}-e^{-a\kappa(t)})da \end{eqnarray}
左辺は$x\in(0,1]$の積分と見れば$\sqrt{x}\kappa(x)\gt0$となりaについて可積分なので,フビニの定理より,
\begin{eqnarray} (LHS)&=&\mathrm{Im}\int_0^1\frac{dx}{1-xt}\int_0^{\infty}a^{s-1}e^{-a\sqrt{x}(\kappa(x)-i\kappa(1-x))}dx\\ &=&\mathrm{Im}\int_0^1\frac{\Gamma(s)}{x^{s/2}(\kappa(x)-i\kappa(1-x))^s}\frac{dx}{1-xt}\\ &=&\Gamma(s)\int_0^1x^{-s/2}\frac{\sin\left(s\tan^{-1}\frac{\kappa(1-x)}{\kappa(x)}\right)}{\left(\kappa(x)^2+\kappa(1-x)^2\right)^{s/2}}\frac{dx}{1-xt}\\ (RHS)&=&\frac{\pi\Gamma(s)}{t}\left(1-\frac{1}{\kappa(t)^s}\right) \end{eqnarray}
以上より,少し変形して,
\begin{eqnarray} \int_0^{1}\frac{\sin\left(s\tan^{-1}\frac{K'(x)}{K(x)}\right)}{\left(K(x)^2+K'(x)^2\right)^{s/2}}\frac{x^{1-s}}{1-x^2t^2}dx=\frac{\pi}{2t^2}\left(\left(\frac{2}{\pi}\right)^s-\frac{1}{K(t)^s}\right) \end{eqnarray}
がわかります.sの範囲は積分の順序交換が可能かつsが実数なので$s\gt0$です.
$s=1,t\to0$を考えれば,
\begin{eqnarray} \int_0^1\frac{K'(x)}{K(x)^2+K'(x)^2}dx&=&\lim_{t\to0}\frac{\pi}{2}\frac{\frac{\pi}{2}-\frac{1}{K(t)}}{t^2}\\ &=&\lim_{t\to0}\frac{\pi}{4}\frac{K(t)\frac{d^2}{dt^2}K(t)-2\left(\frac{d}{dt}K(t)\right)^2}{K(t)^3}\\ &=&\lim_{t\to0}\frac{\pi}{4}\frac{\left(\frac{\pi^2}{8}+O(t^2)\right)-2O(t^2)}{\frac{\pi^3}{8}+O(t^2)}\\ &=&\frac{1}{4} \end{eqnarray}
となる.

\begin{eqnarray} \int_0^{\pi/2}\frac{\cos x}{\sin^2x}\left(1-\frac{x}{\tan x}\right)dx&=&\int_0^1\left(1-\frac{\sqrt{1-x^2}\sin^{-1}x}{x}\right)\frac{dx}{x^2}\\ &=&\int_0^1\frac{dx}{x^2}\int_0^x\left(\frac{\sin^{-1}y}{y^2\sqrt{1-y^2}}-\frac{1}{y}\right)dy \end{eqnarray}
ここで,$|x|\leq1$で$(\sin^{-1}x)^2=\sum_{n\gt0}\frac{x^{2n}}{2n^2\beta_n}$より,$\frac{\sin^{-1}x}{\sqrt{1-x^2}}=\sum_{n\geq0}\frac{x^{2n+1}}{(2n+1)\beta_n}$となることを用います.
\begin{eqnarray} (RHS)&=&\int_0^1\frac{dx}{x^2}\int_0^x\left(\frac{\sin^{-1}y}{y^2\sqrt{1-y^2}}-\frac{1}{y}\right)dy\\ &=&\int_0^1\frac{dx}{x^2}\int_0^x\sum_{n\gt0}\frac{y^{2n-1}}{(2n+1)\beta_n}dy\\ &=&\sum_{n\gt0}\frac{1}{(2n+1)2n(2n-1)\beta_n}\\ &=&\sum_{n\geq0}\frac{1}{(2n+1)^2(2n+3)\beta_n}\\ &=&\sum_{n\geq0}\left(\frac{1}{2n+1}-\frac{1}{2n+3}\right)\frac{1}{2(2n+1)\beta_n}\\ &=&\frac{1}{2}\int_0^1(x^{-1}-x)\frac{\sin^{-1}x}{\sqrt{1-x^2}}dx\\ &=&\frac{1}{2}\int_0^{\pi/2}\frac{x}{\sin x}-x\sin x \ dx \\&=&\beta(2)-\frac{1}{2} \end{eqnarray}

\begin{eqnarray} \int_0^1\frac{1}{(x-\tanh^{-1}x)^2+\pi^2}\frac{dx}{1-x^2}&=&\int_0^\infty\frac{dx}{(\tanh x-x)^2+\pi^2}\ \ \ (\tanh^{-1}x\to x)\\ &=&\frac12\int_{-\infty}^{\infty}\frac{dx}{(\tanh x-x)^2+\pi^2}\\ &=&\frac{1}{2}\int_0^{\infty}\frac{1}{\left(\frac{x^2-1}{x^2+1}-\ln x\right)^2+\pi^2}\frac{dx}{x} \end{eqnarray}
ここで,偏角を$(-\pi,\pi)$として
\begin{eqnarray} f(z):=\frac{1}{\frac{z^2-1}{z^2+1}-\ln z}\frac{1}{z} \end{eqnarray}
の画像のような積分路の複素積分を考えます.

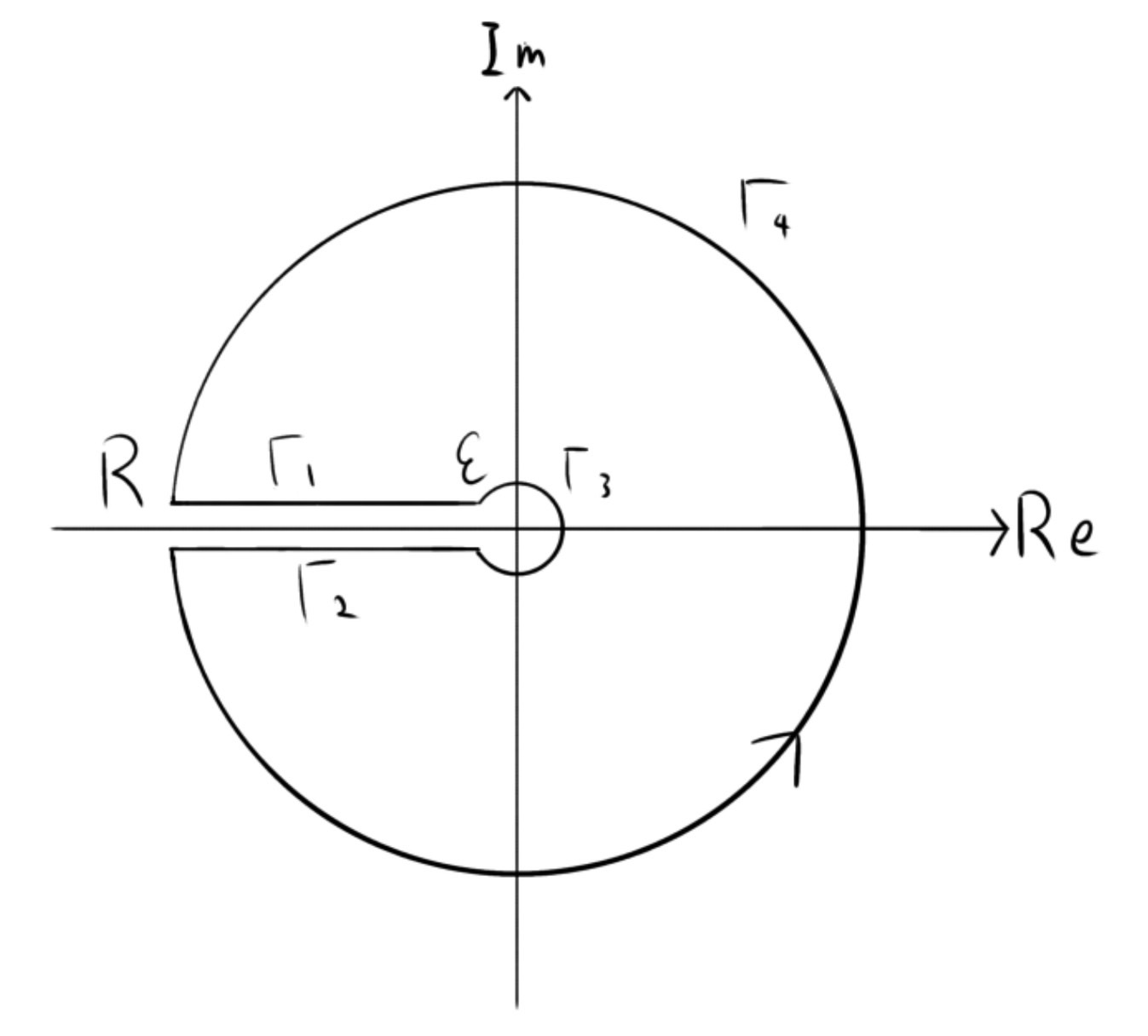
\begin{eqnarray} \int_{\Gamma_1+\Gamma_2}f(z)dz&=&\int_0^{\infty}f(te^{\pi i})-f(te^{-\pi i})dt\\ &=&\int_0^{\infty}\frac{-2\pi i}{\left(\frac{t^2-1}{t^2+1}-\ln t\right)^2+\pi^2}\frac{dt}{t} \end{eqnarray}
そして,$\varepsilon$を$0$または,$\infty$付近の値としたとき $x\in[-\pi,\pi]$に対して,
\begin{eqnarray} \left|\frac{\varepsilon^2e^{2ix}-1}{\varepsilon^2e^{2ix}+1}-\ln \varepsilon-ix\right|&\geq&\left|\frac{\varepsilon^2e^{2ix}-1}{\varepsilon^2e^{2ix}+1}-\ln\varepsilon\right|-\pi\\ &\geq&|-\ln\varepsilon|-\frac{\varepsilon^2+1}{\varepsilon^2-1}-\pi \end{eqnarray}
ですから,
\begin{eqnarray} \left|\int_{\Gamma_3}f(z)dz\right|= \left|\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon e^{ix}dx\right|\leq\frac{2\pi}{-\ln\varepsilon-\frac{\varepsilon^2+1}{\varepsilon^2-1}-\pi}\to0 \end{eqnarray}
と言えます.$\Gamma_4$も同様です.
次に,極を考えます.$\frac{z^2-1}{z^2+1}=\ln z$を満たす複素数を考えればよいです.
\begin{eqnarray} \frac{z^2-1}{z^2+1}=\ln z\Leftrightarrow\frac{\frac{1}{z^2}-1}{\frac{1}{z^2}+1}=\ln\frac{1}{z} \end{eqnarray}
ですから,$z=re^{iw}$が解の時$z=\frac1re^{-iw}$も解になります.
故に$z=re^{iw}\ \ (r\in(0,1],w\in(-\pi,\pi))$について考えれば十分です.
実部比較と虚部比較から,
\begin{eqnarray} \frac{r^4-1}{r^4+2r^2\cos2w+1}=\ln r,\frac{2r^2\sin2w}{r^4+2r^2\cos2w+1}=w \end{eqnarray}
であり,右側の両辺の符号から$w\in(-\frac{\pi}{2},\frac{\pi}{2})$である必要があり,$w\neq0,w\in(-\frac{\pi}{2},\frac{\pi}{2})$で$A=\cos2w-\frac{\sin2w}{w},r^2=-A-\sqrt{A^2-1}$がわかり,実部の方から
\begin{eqnarray} h(w)=\frac{w}{\sin2w}\frac{\sqrt{A^2-1}(\sqrt{A^2-1}+1)}{-A-\sqrt{A^2-1}}-\frac{1}{2}\ln(-A-\sqrt{A^2-1}) \end{eqnarray}
の挙動を見ればよく,$w\neq0,w\in(-\frac{\pi}{2},\frac{\pi}{2})$で$h(w)\gt0$となるので$w=0$以外で解をもちません.$w=0$では,$x\in\mathbb{R},\frac{x^2-1}{x^2+1}=\ln x$の解を考えるだけなので,増減表などから$x=1$のみが解になることがわかります.
以上より,$f(z)$は$z=1$にのみ極があります.
あとは,留数計算ですがwolframより,
\begin{eqnarray} \frac{1}{\frac{(z-1)^2-1}{(z-1)^2+1}-\ln(z-1)}\frac{1}{z-1}=-\frac{3}{z^3}-\frac{3}{2z^2}-\frac{6}{5z}+\frac{3}{5}-\frac{1419z}{2800}+O(z^2) \end{eqnarray}
ですから,
\begin{eqnarray} \oint_{\Gamma_{1+2+3+4}}f(z)dz=-\int_0^{\infty}\frac{2\pi i}{\left(\frac{t^2-1}{t^2+1}-\ln t\right)^2+\pi^2}\frac{dt}{t}=-2\pi i\frac{6}{5} \end{eqnarray}
となり,題意が示せました.

\begin{eqnarray} \int_0^1\frac{\tan^{-1}q\sqrt{p^2x^2+1}}{q\sqrt{p^2x^2+1}}\frac{dx}{(r^2+1)p^2x^2+1}&=&\frac{1}{2pq^2}\int_{q^2}^{q^2(p^2+1)}\frac{\tan^{-1}\sqrt{t}}{\sqrt{t}\sqrt{\frac{t}{q^2}-1}}\frac{dt}{(r^2+1)\left(\frac{t}{q^2}-1\right)+1}\ \ \ (q\sqrt{p^2x^2+1}\to\sqrt{t})\\ &=&\frac{1}{2pq^2r^2}\int_{\frac{1}{q^2(p^2+1)}}^{\frac{1}{q^2}}\frac{\frac{\pi}{2}-\tan^{-1}\sqrt{t}}{\sqrt{\frac{1}{q^2}-t}}\frac{dt}{\frac{r^2+1}{q^2r^2}-t}\ \ \ (t\to t^{-1}) \end{eqnarray}
以下,\begin{eqnarray} \int_0^X\frac{\tan^{-1}\sqrt{t}}{\sqrt{b-t}(a-t)}dt \end{eqnarray}
について考えます.
\begin{eqnarray} \int\frac{dt}{\sqrt{b-t}(a-t)}=-\frac{2}{\sqrt{a-b}}\tan^{-1}\sqrt{\frac{b-t}{a-b}}+C \end{eqnarray}
ですから,
\begin{eqnarray} \int_0^X\frac{\tan^{-1}\sqrt{t}}{\sqrt{b-t}(a-t)}dt=-\frac{2}{\sqrt{a-b}}\int_0^X\tan^{-1}\sqrt{t}d\left(\tan^{-1}\sqrt{\frac{b-t}{a-b}}\right) \end{eqnarray}
となります.
\begin{eqnarray} \alpha+\sum_{n\gt0}\frac{k^n}{n}\sin2n\alpha=\int_0^\alpha\frac{\frac{1+k}{1-k}\frac{1}{\cos^2\alpha}}{1+\left(\frac{1+k}{1-k}\right)^2\tan^2\alpha}d\alpha=\tan^{-1}\left(\frac{1+k}{1-k}\tan\alpha\right) \end{eqnarray}
に基づき,新たに$t$の関数$\alpha,k$と定数$\beta,\gamma$を用いた関数
\begin{eqnarray} S(\alpha,\beta,\gamma;k)=\sum_{n\gt0}\frac{k^n}{n^2}(\cos2n\alpha-\cos2n\beta+\cos2n\gamma-1)-\alpha^2+\beta^2-\gamma^2 \end{eqnarray}
を考えます.
\begin{eqnarray} \frac{dS}{dt}:&=&f(k)\frac{dk}{dt}-2\tan^{-1}\left(\frac{1+k}{1-k}\tan\alpha\right)\frac{d\alpha}{dt}\\ f(k):&=&\sum_{n\gt0}\frac{k^{n-1}}{n}(\cos2n\alpha-\cos2n\beta+\cos2n\gamma-1)=\frac{1}{2k}\ln\frac{(1-2k\cos2n\beta+k^2)(1-k)^2}{(1-2k\cos2n\alpha+k^2)(1-2k\cos2n\gamma+k^2)} \end{eqnarray}
ですから,$\alpha=\tan^{-1}\sqrt{\frac{b-t}{a-b}}$とすれば,
\begin{eqnarray} 2\tan^{-1}\left(\frac{1+k}{1-k}\sqrt{\frac{b-t}{a-b}}\right)\frac{d(\tan^{-1}\sqrt{\frac{b-t}{a-b}})}{dt}=-\frac{dS}{dt}+f(k)\frac{dk}{dt} \end{eqnarray}
となることがわかります.$\frac{dk}{dt}$の項が邪魔なので$f(k)=0$,つまり,
$(1-2k\cos2n\alpha+k^2)(1-2k\cos2n\gamma+k^2)-(1-2k\cos2n\beta+k^2)(1-k)^2=0$
という二次方程式を解けばいいのですが,
\begin{eqnarray} k=\frac{A-1}{A+1},A:=\sqrt{\frac{1}{\tan^2\alpha\tan^2\gamma}-\frac{\cos^2\beta}{\sin^2\alpha\sin^2\gamma}} \end{eqnarray}
がその解のようです.よって$k=\frac{A-1}{A+1}$とすれば,
\begin{eqnarray} 2\tan^{-1}\left(A\sqrt{\frac{b-t}{a-b}}\right)\frac{d(\tan^{-1}\sqrt{\frac{b-t}{a-b}})}{dt}=-\frac{dS}{dt} \end{eqnarray}
となります.最後に,$A=\sqrt{\frac{a-b}{b-t}}\sqrt{t}$となるように,$\beta,\gamma$を決定できれば良いのですが,それは,係数比較により$(a-b)\cos^2\gamma-a\cos^2\beta=0,\cos^2\beta=(a-b)\sin^2\gamma$
がわかるので,$\beta=\tan^{-1}\sqrt{\frac{b+1}{a-b}},\gamma=\tan^{-1}\frac{1}{\sqrt{a}}$とすれば,
\begin{eqnarray} 2\tan^{-1}\sqrt{t}\frac{d(\tan^{-1}\sqrt{\frac{b-t}{a-b}})}{dt}=-\frac{dS}{dt} \end{eqnarray}
となり,
\begin{eqnarray} \int^X\frac{\tan^{-1}\sqrt{t}}{\sqrt{b-t}(a-t)}dt=\frac{1}{\sqrt{a-b}}S\left(\tan^{-1}\sqrt{\frac{b-X}{a-b}},\tan^{-1}\sqrt{\frac{b+1}{a-b}},\tan^{-1}\frac{1}{\sqrt{a}};\frac{A-1}{A+1}\right)+C \end{eqnarray}
がわかりました.よって,
\begin{eqnarray} \int_0^1\frac{\tan^{-1}\frac{1}{q\sqrt{p^2x^2+1}}}{q\sqrt{p^2x^2+1}}\frac{dx}{(r^2+1)p^2x^2+1}&=&\frac{1}{2pq^2r^2}\int_{\frac{1}{q^2(p^2+1)}}^{\frac{1}{q^2}} \frac{\tan^{-1}\sqrt{t}}{\sqrt{\frac{1}{q^2}-t}\left(\frac{r^2+1}{q^2r^2}-t\right)}dt\\ &=&\frac{1}{2pqr}\left(S\left(0,\tan^{-1}r\sqrt{q^2+1},\tan^{-1}\frac{qr}{\sqrt{r^2+1}};1\right)-S\left(\tan^{-1}\frac{pr}{\sqrt{p^2+1}},\tan^{-1}r\sqrt{q^2+1},\tan^{-1}\frac{qr}{\sqrt{r^2+1}};\frac{1-pqr}{1+pqr}\right)\right) \end{eqnarray}
第二項の$k$に注目すると$pqr=1$であれば,$k=0$となり,簡単に値が出せます.そのため,$pqr=1$とすると,$\sum_{n\gt0}\frac{\cos(2n\tan^{-1}x)}{n^2}=\frac{\pi^2}{12}+\left(\tan^{-1}\frac{1}{x}\right)^2$を用いて,
\begin{eqnarray} \int_0^1\frac{\tan^{-1}\frac{1}{q\sqrt{p^2x^2+1}}}{q\sqrt{p^2x^2+1}}\frac{dx}{(r^2+1)p^2x^2+1}&=&\frac{1}{2}\left(\left(\tan^{-1}\frac{pr}{\bar{p}}\right)^2-\left(\tan^{-1}\frac{1}{\bar{q}r}\right)^2+\left(\tan^{-1}\frac{\bar{r}}{qr}\right)^2\right)\\ &=&\frac{1}{2}\left(\left(\tan^{-1}\frac{1}{\bar{p}q}\right)^2-\left(\tan^{-1}\frac{1}{\bar{q}r}\right)^2+\left(\tan^{-1}\bar{r}p\right)^2\right) \end{eqnarray}
であり,$\int_0^1\frac{\frac{\pi}{2}}{q\sqrt{p^2x^2+1}}\frac{dx}{(r^2+1)p^2x^2+1}=\frac{\pi}{2}\tan^{-1}\frac{1}{\bar{p}q}$なので,
\begin{eqnarray} \int_0^1\frac{\tan^{-1}q\sqrt{p^2x^2+1}}{q\sqrt{p^2x^2+1}}\frac{dx}{(r^2+1)p^2x^2+1}=\frac{\pi^2}{8}-\frac{1}{2}(\tan^{-1}\bar{p}q)^2+\frac12\left(\tan^{-1}\frac{1}{\bar{q}r}\right)^2-\frac{1}{2}(\tan^{-1}\bar{r}p)^2 \end{eqnarray}
がわかりました.