積分問題集の解説(上級)
\begin{eqnarray} \int_{0}^{1}\frac{\ln x\ln(1+x)}{x(1+x)}dx=-\frac{5}{8}ζ(3) \end{eqnarray}
級数展開により多重ゼータ値に帰着させます.
\begin{eqnarray} \int_{0}^{1}\frac{\ln x}{x(1+x)}\ln(1+x)dx&=&\int_{0}^{1}\frac{\ln x}{x(1+x)}\int_{0}^{x}\frac{dtdx}{1+t}\\ &=&\sum_{n,m≥0}(-1)^{m+n}\int_{0}^{1}x^{m-1}\ln x\int_{0}^{x}t^mdtdx\\ &=&\sum_{n,m≥0}\frac{(-1)^{n+m+1}}{(n+m+1)^2(m+1)}\\ &=&\sum_{n≥m>0}\frac{(-1)^n}{n^2m}\\ &=&ζ(\bar{3})+ζ(1,\bar{2})\\ &=&-\frac{5}{8}ζ(3) \end{eqnarray}
途中多重ゼータ値が出てきました.
$ζ(1,\bar{2})=\frac{1}{8}ζ(3)$
はwataruさんの下の記事で示されています.
シャッフル積,調和積により計算できるようですね.
あとは部分積分によりポリログの積分にして解くという発想がありますが試していません.
まめけびさんの調和数を含んだ級数seriesでも求められていました.
[調和数を含む級数とゼータ]
( https://mamekebi-science.com/math/series/harmonicseries-dedoelder1/ )
\begin{eqnarray} \int_{0}^{π/2}\frac{x}{\sqrt{\tan x}}dx=\frac{π}{2\sqrt{2}}(\frac{π}{2}-\ln 2) \end{eqnarray}
これは$\int_{0}^{π}\sin^{s-1}x\sin{tx}dx$を求めてtで偏微分しt=1/2,s=1/2を代入することで求めることができます.
今回は問題を作っていた際にNKSさんから頂いた面白い計算方法を紹介します.
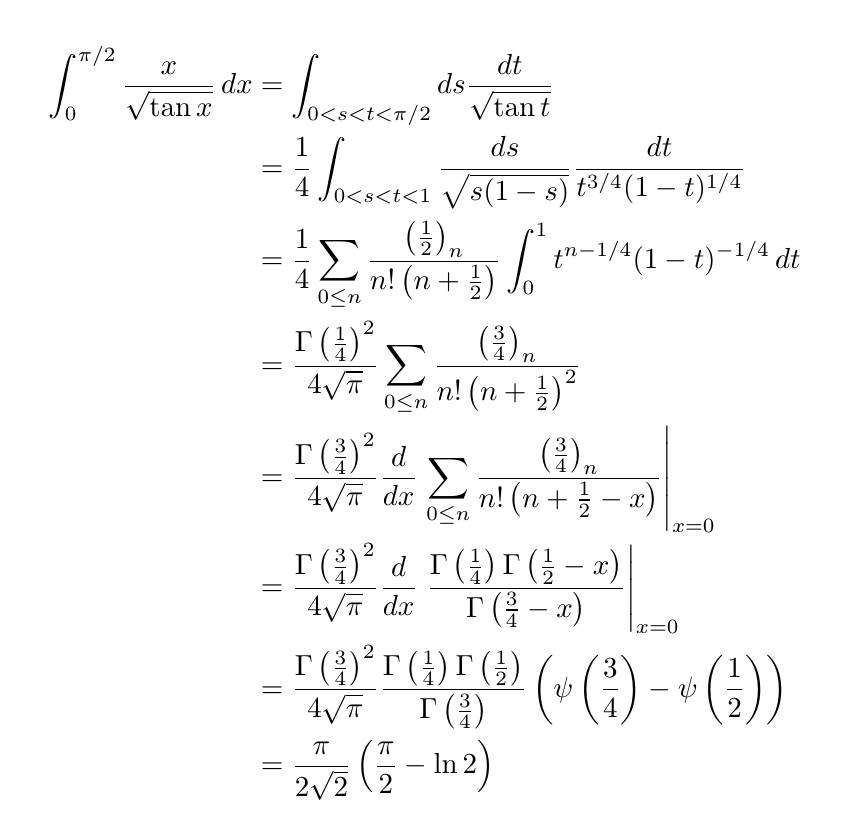
こういった複雑な積分を反復積分により級数にするという操作は魅力がありますね!
最近はなんらかの積分でこういった操作をできないか色々試して結構慣れてきた気がします.
やはりどんな事も回数を重ねる事が大事ですね.
\begin{eqnarray} \int_{0}^{1}\left(\frac{\arctan x}{x}\right)^3dx=\frac{3}{2}β(2)+\frac{3π}{8}\ln 2-\frac{3π^2}{32}-\frac{π^3}{64} \end{eqnarray}
ここで$β(2)$とはカタラン定数($\sum_{n≥0}\frac{(-1)^n}{(2n+1)^2}$)です.
これは誰かが一般化できそうと話していた気がしますが結局は出来ていないっぽいですね.
僕も検討しましたがうまい具合にはできそうにない気がします.
今回の問題は結構都合の良い形になっているので簡単に解けますね.
\begin{eqnarray}
\int_{0}^{1}\frac{\arctan^3x}{x^3}dx&=&\left[-\frac{x^{-2}}{2}\arctan^3x\right]_0^1+\frac{3}{2}\int_{0}^{1}\frac{\arctan^2x}{x^2}+\frac{\arctan^2x}{1+x^2}dx\\
&=&-\frac{π^3}{64}+\frac{3}{2}\int_{0}^{1}\frac{\arctan^2x}{x^2}dx
\end{eqnarray}
\begin{eqnarray}
\int_{0}^{1}\frac{\arctan^2x}{x^2}dx
&=&-\frac{π^2}{16}+2\int_{0}^{π/4}\frac{x\cos x}{\sin x}dx\\
&=&-\frac{π^2}{16}-\frac{π}{4}\ln 2 -2\int_{0}^{π/4}\ln\sin xdx\\
&=&-\frac{π^2}{16}+\frac{π}{4}\ln 2
+2\sum_{n>0}\int_{0}^{π/4}\frac{\cos 2nx}{n}dx\\
&=&-\frac{π^2}{16}+\frac{π}{4}\ln 2+β(2)
\end{eqnarray}
\begin{eqnarray}
\therefore \int_{0}^{1}\left(\frac{\arctan x}{x}\right)^3dx=\frac{3}{2}β(2)+\frac{3π}{8}\ln 2-\frac{3π^2}{32}-\frac{π^3}{64}
\end{eqnarray}
途中対数三角関数のフーリエ級数である
$\ln 2\sin x=-\sum_{n>0}\frac{\cos 2nx}{n}$
を使いました.
\begin{eqnarray} \int_{0}^{π/2}\frac{x^4}{\tan x}dx=\frac{π^2}{16}\ln 2+\frac{93}{32}ζ(5)- \frac{9π^2}{16}ζ(3) \end{eqnarray}
パット見面倒くさそうですね
実際結構面倒くさいです.
そして右辺$\ln 2$の係数が他の値と比べてみるとweightが違うように感じます.
実際wolframに入れてみると$π$の指数が4であることがわかります.
多分typoですね.
これはなんとxの指数部分における一般化を出せたのでそれを証明しようと思います.
今回用いるのは次のような変形です.
\begin{eqnarray}
\int_{0}^{π/2}x^n\cot xdx&=& \Re\int_{0}^{π/2}x^n\frac{2i}{1-e^{-2ix}}e^{-2ix}dx\\
&=&\Re\lim_{m→∞}\int_{0}^{π/2}\frac{1-e^{-2imx}}{1-e^{-2ix}}x^ne^{-2ix}\\
&=&\lim_{m→∞}\sum_{l=1}^{m}\int_{0}^{π/2}x^ne^{-2ixl}dx
\end{eqnarray}
途中で無限和のようなものと積分を入れ替えましたがそもそも総和の極限が元から外にあるのでこれは項別積分しただけです.
そしていきなり出てきた極限ですが計算(部分積分と挟み込み)をしてみると0になる事がわかります.
なら最初から部分積分した$\ln \cos$のフーリエ級数を用いればいいではないかとなるんですがなんとなくこっちの方が見通しがいい気がするのでこの方法で進めます.
先ほどの変形から求めるべきは次の積分であることがわかります.
\begin{eqnarray} \int_{0}^{x}x^n e^{-2ixl}dx \end{eqnarray}
不定積分となっていますがどちらにせよやることは同じなので区間についても一般化した感じです.
これはこの問題1の積分を$I_n$
と置き部分積分することで漸化式に変形する事で解きます.
\begin{eqnarray}
I_n=-\frac{x^ne^{-2ixl}}{2il}+\frac{n}{2il}I_{n-1}
\end{eqnarray}
\begin{eqnarray}
⇒\frac{(2il)^n}{n!}I_n-\frac{(2il)^{n-1}}{(n-1)!}I_{n-1}=-(2il)^{n-1}x^n\frac{e^{-2ixl}}{n!}
\end{eqnarray}
\begin{eqnarray}
\frac{(2il)^n}{n!}I_n&=&I_0-\sum_{k=1}^{n}\frac{(2il)^{k-1}}{k!}x^ke^{-2ixl}\\
I_n&=&\frac{n!(1-e^{-2ilx})}{(2il)^{n+1}}-\sum_{k=1}^{n}\frac{n!}{k!(2il)^{n+1-k}}x^ke^{-2ixl}
\end{eqnarray}
汚すぎます.
$x→π/2$とし実部をとりlについての無限和を取りましょう.
補題意自体を$I$とおきます
\begin{eqnarray} I&=&\Re\sum_{l>0}\frac{n!}{2^nl^{n+1}}(1-(-1)^l)\cos(πn/2) -(-1)^l\sum_{k=1}^{n}\frac{n!π^k}{2^nl^{n+1-k}k!}\cos(\frac{π(n-k)}{2})\\ &=&\frac{n!\cos\frac{πn}{2}}{2^n}(ζ(n+1)-ζ(\overline{n+1}))-\frac{n!}{2^n}\sum_{k=1}^{n}\frac{π^k}{k!}ζ(\overline{n+1-k})\cos\frac{π(n-k)}{2} \end{eqnarray}
汚すぎます.
今回の題意であるn=4を代入して見ましょう.
\begin{eqnarray}
\frac{4!}{2^4}(ζ({5})-ζ(\bar{5}))-\frac{4!}{2^4}\sum_{k=1}^{4}\frac{π^k}{k!}\cos\frac{π(4-k)}{2}ζ(\overline{5-k})
\end{eqnarray}
\begin{eqnarray}
&=&\frac{3}{2}(2-\frac{1}{2^4})ζ(5)+\frac{3π^2}{4}ζ(\bar{3})+\frac{π^4}{16}\ln 2\\
&=&\frac{π^4}{16}\ln 2+\frac{93}{32}ζ(5)-\frac{9π^2}{16}ζ(3)
\end{eqnarray}
一致しましたね.
もうすでにかなり濃い内容ですが更に話したいことがあります.
反復ベータ積分についてです.
\begin{eqnarray}
\int_{0}^{x}\frac{t^{2n-1}}{\sqrt{1-t^2}}dt=\frac{1}{2nβ_n}\sum_{m≥n}β_mx^{2m}\sqrt{1-x^2}
\end{eqnarray}
\begin{eqnarray}
\int_{0}^{x}\frac{t^{2n}}{\sqrt{1-t^2}}dt=β_n\sum_{m>n}\frac{x^{2m-1}}{2mβ_m}\sqrt{1-x^2}
\end{eqnarray}
$β_n:=\binom{2n}{n}2^{-2n}$
積分botにて次の積分が出されていました.
\begin{eqnarray} \int_{0}^{x}\frac{t^3}{\tan t}dt=\frac{x}{4}\sum_{n>0}\frac{\sin^{2n}x}{n^3β_n}-\frac{\cos x}{8}\sum_{m>n>0}\frac{\sin^{2m-1}x}{n^3mβ_m}\\ \end{eqnarray}
早速証明です
\begin{eqnarray}
\int_{0}^{x}\frac{t^3}{\tan t}dt&=&\int_{0}^{\sin x}\frac{\arcsin^3 t}{t}dt\\
&=&\int_{0}^{x}\frac{\arcsin^2t}{t}\int_{0}^{t}\frac{dsdt}{\sqrt{1-s^2}}\\
&=&\sum_{n>0}\frac{1}{2n^2β_n}\int_{0}^{\sin x}t^{2n-1}\int_{0}^{t}\frac{dsdt}{\sqrt{1-s^2}}\\
&=&\sum_{n>0}\frac{1}{4n^3β_n}\int_{0}^{\sin x}\frac{\sin^{2n}x-s^{2n}}{\sqrt{1-s^2}}ds\\
&=&\frac{x}{4}\sum_{n>0}\frac{\sin^{2n}x}{n^3β_n}-\frac{\cos x}{8}\sum_{m>n>0}\frac{\sin^{2m-1 }x}{n^3mβ_m}
\end{eqnarray}
また$x=π/2$のとき
\begin{eqnarray}
\sum_{n>0}\frac{1}{4n^3β_n}\int_{0}^{1}\frac{1-t^{2n}}{\sqrt{1-t^2}}dt=\frac{π}{8}\sum_{n>0}\frac{1}{n^3β_n}-\frac{1}{n^3}
\end{eqnarray}
では同様の展開を4乗の場合にもやってみしょう.
\begin{eqnarray} \int_{0}^{\sin x}\frac{\arcsin^4t}{t}dt&=&2!\int_{0}^{\sin x}\frac{\arcsin^2t}{t}\int_{0}^{t}\frac{1}{\sqrt{1-s^2}}\int_{0}^{s}\frac{dudsdt}{\sqrt{1-u^2}}\\ &=&\frac{1}{2}\sum_{n>0}\frac{1}{n^3β_n}\int_{0}^{\sin x}\frac{\sin^{2n}x-s^{2n}}{\sqrt{1-s^2}}\int_{0}^{s}\frac{duds}{\sqrt{1-u^2}}\\ &=&\frac{x^2}{4}\sum_{n>0}\frac{\sin^{2n}x}{n^3β_n}-\frac{1}{4}\sum_{m>n>0}\frac{1}{n^3mβ_m}\int_{0}^{\sin x}\frac{\sin^{2n-1}x\cos x-s^{2n-1}\sqrt{1-s^2}}{\sqrt{1-s^2}}ds\\ &=&\frac{x^2}{4}\sum_{n>0}\frac{\sin^{2n}x}{n^3β_n}-\frac{x\cos x}{4}\sum_{m>n>0}\frac{\sin^{2m-1}x}{n^3mβ_m}+\frac{1}{8}\sum_{m>n>0}\frac{\sin^{2m}x}{m^3n^2β_n} \end{eqnarray}
ここから何らかの級数が得られそうで面白いですね
\begin{eqnarray} \int_{0}^{\infty}\frac{\cos αx}{\cosh x+\cos βπ}dx=\frac{π\sinh αβπ}{\sinh απ\sin βπ} \end{eqnarray}
まず,被積分関数には次のような級数表示があります.
\begin{eqnarray}
\frac{1}{\cosh x+\cos t}=\frac{2}{\sin t}\sum_{n>0}(-1)^{n-1}\sin nt \ e^{-nx}
\end{eqnarray}
証明はいたって簡単です.
\begin{eqnarray} \frac{1}{\cos x+\cos t}&=&\frac{2e^{-x}}{(e^{-x}+e^{ix})(e^{-x}+e^{-ix})}\\ &=&\frac{e^{-x}}{i\sin t}(\frac{1}{e^{-x}+e^{-it}}-\frac{1}{e^{-x}+e^{it}})\\ &=&\frac{e^{-x}}{i\sin t}\sum_{n>0} (-1)^n e^{-nx}(e^{(n+1)it}-e^{-(n+1)it})\\ &=&\frac{2}{\sin t}\sum_{n>0}(-1)^{n-1}\sin nt \ e^{-nx} \end{eqnarray}
では積分の証明です.
\begin{eqnarray} \int_{0}^{\infty}\frac{\cos αx}{\cosh x+\cos βπ}dx&=&\frac{2}{\sin βπ}\sum_{n>0}(-1)^{n-1}\sin βπn \int_{0}^{\infty}\cos αx e^{-nx}dx\\ &=&\frac{2}{\sin βπ}\sum_{n>0}\frac{(-1)^{n-1}n\sin βπn}{n^2+α^2}\\ &=&\frac{π\sinh αβπ}{\sinh απ\sin βπ} \end{eqnarray}
途中次の級数を使いました.
\begin{eqnarray}
\sum_{n>0}\frac{n\sin πx}{n^2+a^2}=\frac{π\sinh a(π-x)}{2\sinh aπ}
\end{eqnarray}
留数定理により証明できます.
\begin{eqnarray} \int_{0}^{π}\sin^{2n+1}x e^{-tx}dx=\frac{(2n+1)!}{\prod_{k=0}^{n}(t^2+(2k+1)^2}(1+e^{-πt}) \end{eqnarray}
これは高校範囲で証明可能です!
部分積分により漸化式に持ち込みます.
\begin{eqnarray}
I_{n+1}:&=&\int_{0}^{π}\sin^{2n+1}x e^{-tx}dx\\
&=&\frac{2n+1}{t}\int_{0}^{π}\cos x\sin^{2n}x e^{-tx}dx\\
&=&\frac{2n+1}{t^2}\int_{0}^{π}(2n\sin^{2n-1}x(1-\sin^2x)-\sin^{2n+1}x)e^{-tx}dx\\
&=&\frac{(2n+1)2n}{t^2}I_n-\frac{(2n+1)^2}{t^2}I_{n+1}
\end{eqnarray}
\begin{eqnarray}
⇒I_{n+1}=\frac{(2n+1)2n}{t^2+(2n+1)^2}I_n
\end{eqnarray}
\begin{eqnarray}
⇒I_{n+1}&=&\frac{(2n+1)!}{\prod_{k=1}^n(t^2+(2k+1)^2)}I_1\\
&=&\frac{(2n+1)!}{\prod_{k=0}^{n}(t^2+(2k+1)^2)}(1+e^{-πt})
\end{eqnarray}
ここまで計算してみると区間が$[0,πn]$のときは$\sin x$により,
$[0,∞)$のときは$e^{-tx}$により
良い具合に漸化式を作るれることに気づきます.
実際,同様の計算により
\begin{eqnarray}
\int_{0}^{\infty}\sin^{2n+1}x e^{-tx}dx=\frac{(2n+1)!}{\prod_{k=0}^{n}(t^2+(2k+1)^2)}
\end{eqnarray}
がわかります.
そして,これがある問題に使えます.
初級で解説した時に与えられた次の問題です.
\begin{eqnarray} \int_{0}^{\infty}\prod_{k=0}^{n}\frac{1}{x^2+(2k+1)^2}dx=\frac{π}{2^{2n+1}(2n+1)n!^2} \end{eqnarray}
次のような変形ができます.
\begin{eqnarray}
\int_{0}^{\infty}\prod_{k=0}^{n}\frac{1}{x^2+(2k+1)^2}dx&=&
\frac{1}{(2n+1)!}\int_{0}^{\infty}\int_{0}^{\infty}\sin^{2n+1}y e^{-xy}dydx\\
&=&\frac{1}{(2n+1)!}\int_{0}^{\infty}\sin^{2n+1}y\int_{0}^{\infty}e^{-xy}dxdy\\
&=&\frac{1}{(2n+1)!}\int_{0}^{\infty}\frac{\sin^{2n+1}x}{x}dx
\end{eqnarray}
なんとこんな簡単な形に変形できるんですね.
また次のようなこともわかります.
\begin{eqnarray}
\int_{0}^{\infty}\sin^{2n+1}x e^{-tx}dx&=&\frac{1}{2^{2n+1}}(-1)^{n-1}i\int_{0}^{\infty}\sum_{k=0}^{2n+1}\binom{2n+1}{k}(-1)^ke^{ix(2n+1-2k)}e^{-tx}dx\\
&=&\frac{i}{2^{2n+1}}\sum_{k=0}^{2n+1}\binom{2n+1}{k}\frac{(-1)^{n-k-1}}{t-i(2n+1-2k)}\\
&=&\frac{1}{2^{2n+1}}\sum_{k=0}^{2n+1}\binom{2n+1}{k}\frac{2n-2k+1}{t^2+(2n-2k+1)^2}(-1)^{n-k}\\
&=&\frac{1}{2^{2n}}\sum_{k=0}^{n}\binom{2n+1}{k}\frac{2k+1}{t^2+(2k+1)^2}(-1)^k
\end{eqnarray}
つまり
\begin{eqnarray}
\prod_{k=0}^{n}\frac{1}{t^2+(2k+1)^2}=\frac{1}{2^{2n}(2n+1)!}\sum_{k=0}^{n}\binom{2n+1}{k}\frac{2k+1}{t^2+(2k+1)^2}
\end{eqnarray}
と部分分数分解できます.
\begin{eqnarray} \int_{0}^{\infty}\frac{x^{s-1}}{1+x^2}\frac{\sin(x-s\arctan\frac{1}{ax})}{(1+a^2x^2)^{s/2}}dx=\frac{π}{2e(1+a)^s} \end{eqnarray}
これはかなり難しいです.
特徴としては前回の解説同様に
$\frac{1}{(a+ib)^s}$が関係してきます.
\begin{eqnarray}
\int_{0}^{\infty}\frac{x^{s+1}}{1+x^2}\frac{\sin(x-s\arctan\frac{1}{ax})}{(1+a^2x^2)^{s/2}}dx&=&
\Im\int_{0}^{\infty}\frac{1}{1+x^2}\frac{e^{ix}}{(a+i/x)^s}dx\\
&=&\Im\frac{1}{Γ(s)}\int_{0}^{\infty}\frac{e^{ix}}{1+x^2}\int_{0}^{\infty}t^{s-1}e^{-t(a+i/x)}dtdx\\
&=&\frac{1}{Γ(s)}\int_{0}^{\infty}t^{s-1}e^{-at}\int_{0}^{\infty}\frac{x\sin(x-\frac{t}{x})}{1+x^2}dxdt
\end{eqnarray}
ここでxの積分を解きます.
\begin{eqnarray}
I(t):&=&\int_{0}^{\infty}\frac{x\sin(x-\frac{1}{x})}{1+x^2}dx\\
I'(t)&=&-\int_{0}^{\infty}\frac{\cos(x-\frac{t}{x})}{1+x^2}dx\\
I''(t)&=&-\int_{0}^{\infty}\frac{\sin(x-\frac{t}{x})}{1+x^2}\frac{dx}{x}\\
I(0)&=&\frac{π}{2e}
\end{eqnarray}
\begin{eqnarray}
I(t)-I''(t)&=&\int_{0}^{\infty}\frac{\sin(x-\frac{t}{x})}{x}dx\\
&=&-\int_{0}^{\infty}\frac{\sin(x-\frac{t}{x})}{x}dx (x→\frac{t}{x})\\
&=&-0
\end{eqnarray}
\begin{eqnarray}
\therefore I(t)=\frac{π}{2}e^{-t-1}
\end{eqnarray}
なんと微分方程式によりあっさり解決できました.綺麗ですね.
先ほどの計算から始めます.
\begin{eqnarray}
&=&\frac{π}{2eΓ(s)}\int_{0}^{\infty}
t^{s-1}e^{-at}dt\\
&=&\frac{π}{2e(a+1)^s}
\end{eqnarray}
かなり計算が多いですね.
初手から行っていたガンマ関数への変形を施せばこういった問題に対処できる可能性があると思います.
また途中でてきた$I(t)$は便利さんによりかなり前に解説されています.(どこで解説されていたかは覚えていません…)
その際の手法は次の記事のような置換だったと記憶しています.
\begin{eqnarray} \int_{0}^{\infty}\left(\frac{\sin x}{x}\arcsin a\sin x\right)^2=\frac{π}{4}\mathrm{Li}_2(a^2) \end{eqnarray}
今回は次の公式を使います.
$f(x)=f(π-x)=f(x+π)$なる$f$について次が成り立つ
\begin{eqnarray}
\int_{0}^{\infty}\frac{\sin^2x}{x^2}f(x)dx=\int_{0}^{\infty}\frac{\sin x}{x}f(x)=\int_{0}^{π/2}f(x)dx
\end{eqnarray}
(詳細は
wikipedia
へ)
証明は
ここ
でされています.
三角関数の分数展開によるものですね.
今回の関数は条件を満たすので範囲を変えて積分していきましょう.
\begin{eqnarray} \int_{0}^{π/2}\arcsin^2a\sin xdx&=&\int_{0}^{1}\frac{\arcsin^2ax}{\sqrt{1-x^2}}dx\\ &=&\sum_{n>0}\frac{a^{2n}}{2n^2β_n}\int_{0}^{1}\frac{x^{2n}}{\sqrt{1-x^2}}dx\\ &=&\frac{π}{4}\sum_{n>0}\frac{a^{2n}}{n^2} \end{eqnarray}
種がわかってしまえば簡単ですがその種がめちゃくちゃ難しいですよね.この問題にぶつかって全く歯が立たないとなってこの解説を読めばロバーチェフスキーの積分公式が偉大に見えそうです.(経験者は語る)
そしてこれはexc3に解を与えます.
\begin{eqnarray}
\int_{0}^{\infty}\frac{\sin^{2n+1}x}{x}dx&=&\int_{0}^{π/2}\sin^{2n}xdx\\
&=&\frac{(2n)!π}{2^{2n+1}n!^2}
\end{eqnarray}
\begin{eqnarray} \int_{0}^{\infty}x\ln\left(1+\frac{1}{\cosh x}\right)dx=\frac{21}{16}ζ(3) \end{eqnarray}
この問題はNKSさんがすごい解法を見せてくださったのでそれを共有します!
問題2と同様に反復積分に持ち込みます.
\begin{eqnarray} \int_{0}^{\infty}x\ln\left(1+\frac{1}{\cosh x}\right)dx&=&\int_{0< t< x}\ln\left(1+\frac{1}{\cosh x}\right)tdtdx\\ &=&\int_{0< s< t<1}\frac{\ln(1+s)}{s\sqrt{1-s^2}}\frac{dsdt}{\sqrt{1-t^2}} (\frac{1}{\cosh x}→s,\frac{1}{\cosh t}→t)\\ &=&\int_{0< u< s< t<1}\frac{dt}{t\sqrt{1-t^2}}\frac{ds}{s\sqrt{1-s^2}}\frac{du}{1+u} (\frac{dt}{t\sqrt{1-t^2}}→\frac{dt}{t},\frac{ds}{s\sqrt{1-s^2}})→\frac{ds}{s},\frac{du}{u\sqrt{1-u^2}}→\frac{du}{u\sqrt{1-u^2}}(これらの微分方程式の解はy=\frac{2x}{1+x^2}))\\ &=&2\int_{0< u< s< t<1}\frac{dt}{t}\frac{ds}{s}\frac{1-u}{(1+u^2)(1+u)}du\\ &=&2\int_{0< u< s< t<1}\frac{dt}{t}\frac{ds}{s}\left(\frac{1}{1+u}-\frac{u}{1+u^2}\right)\\ &=&2\sum_{n>0}(-1)^n\int_{0< u< s< t<1}\frac{dt}{t}\frac{ds}{s}(u^n-u^{2n+1})du\\ &=&\frac{21}{16}ζ(3) \end{eqnarray}
途中で都合の良い置換をするために微分方程式を解くのは凄いテクニックですよね.
この置換は反復積分においてかなり有用らしいです.
また次のような解法もあります.
\begin{eqnarray}
\int_{0}^{\infty}\frac{x^{s-1}}{\cosh x+\cos t}\sin tdx=2Γ(s)\sum_{n>0}\frac{(-1)^{n-1}}{n^s}\sin nt
\end{eqnarray}
\begin{eqnarray}
⇒\int_{0}^{\infty}x^{s-1}\ln(1+\frac{1}{\cosh x})dx=2Γ(s)\sum_{n>0}\frac{(-1)^{n-1}}{n^{s+1}}(\cos\frac{πn}{2}-1)
\end{eqnarray}
上のメリン変換は問題5と同様にして示せます.
\begin{eqnarray} \int_{0}^{1}\frac{\ln(1-x)}{1+s^2x^2}dx=\frac{\arctan s\ln(1+s^2)}{2s}-\sum_{n≥0}\frac{(-1)^n}{(2n+1)^2}s^{2n} \end{eqnarray}
これはものすごく難しいです.
級数展開により右辺と一致することを示します.
\begin{eqnarray}
\int_{0}^{1}\frac{\ln(1-x)}{1+s^2x^2}dx&=&\sum_{n≥0}(-1)^ns^{2n}\int_{0}^{1}x^{2n}\ln(1-x)dx\\
&=&\sum_{n≥0}\frac{(-1)^ns^{2n}}{2n+1}(ψ(1)-ψ(2n+2))\\
&=&\sum_{n≥0}\frac{(-1)^{n-1}s^{2n}}{2n+1}H_{2n+1}\\
&=&-\sum_{n≥0}\frac{(-1)^n}{(2n+1)^2}s^{2n}+\sum_{n>0}\frac{(-1)^{n-1}}{2n+1}H_{2n}s^{2n}
\end{eqnarray}
\begin{eqnarray}
\arctan x\ln(1+x^2)&=&\left(\int_{0}^{x}\frac{1}{1+t^2}dx\right)\left(\int_{0}^{x}\frac{2s}{1+s^2}ds\right)\\
&=&\left(\int_{0< t< s< x}+\int_{0< s< t< x}\right)\frac{dt}{1+t^2}\frac{2s}{1+s^2}ds\\
&=&2\sum_{m,n≥0}(-1)^{m+n}x^{2m+2n+3}\left(\frac{1}{2(n+1)(2m+2n+3)}+\frac{1}{(2m+1)(2m+2n+3)}\right)\\
&=&2\sum_{m≥n>0}\frac{(-1)^{m-1}}{2m+1}x^{2m+1}(\frac{1}{2n}+\frac{1}{2n-1})\\
&=&2\sum_{m>0}\frac{(-1)^{m-1}}{2m+1}H_{2m}x^{2m+1}
\end{eqnarray}
\begin{eqnarray}
\therefore \int_{0}^{1}\frac{\ln(1-x)}{1+s^2x^2}dx=\frac{\arctan s\ln(1+s^2)}{2s}-\sum_{n≥0}\frac{(-1)^n}{(2n+1)^2}s^{2n}
\end{eqnarray}
難しいですね…
これの両辺をsで不定積分し適切な変形を施す事で次が示せます.
\begin{eqnarray}
\int_{0}^{1}\frac{\arctan{sx}}{x}\ln\frac{\sqrt{1+s^2x^2}}{1-x}dx=\sum_{n≥0}\frac{(-1)^{n}}{(2n+1)^3}s^{2n+1}
\end{eqnarray}
これは元々
Necrooo
さんから提唱された問題でなんと$|s|≥1$でも成り立つそうです.
僕はまだ$|s|≤1$しか示せていないのでまだ謎はありますね.
