任意のポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求める方法(日曜数学会)
タイトル画像 使用ツール Bing Image Creator : 提供 DALL-E3
はじめに
この記事は 第$28$回日曜数学会($2023.10.29$) で発表した内容に加筆したものです。
また、記事の内容は過去の記事
・ ドミノタイリングの数え上げ公式の導出方法【前編～導出～】
・ ドミノタイリングの数え上げ公式の導出方法【後編～証明～】
を読んでいることを前提として、過去の記事で使った用語や定理を説明せずに使っている部分がありますので、未読の方は先にこれらの記事を読んでからこの記事を読むことをお勧めします。
……が、記事の前半部分はこの記事単独でも理解できるように作りましたので、お急ぎの方は前半だけでも読んでいただければと思います。
ドミノで埋め尽くす方法の総数
この記事では、ポリオミノ(単位正方形を辺でつないだ多角形)をドミノ(ポリオミノのうち$1\times2$ の大きさのもの)で埋め尽くす方法の総数を、行列式を使って「機械的に」「あっという間に」計算できる、私が考案したアルゴリズムをご紹介します。
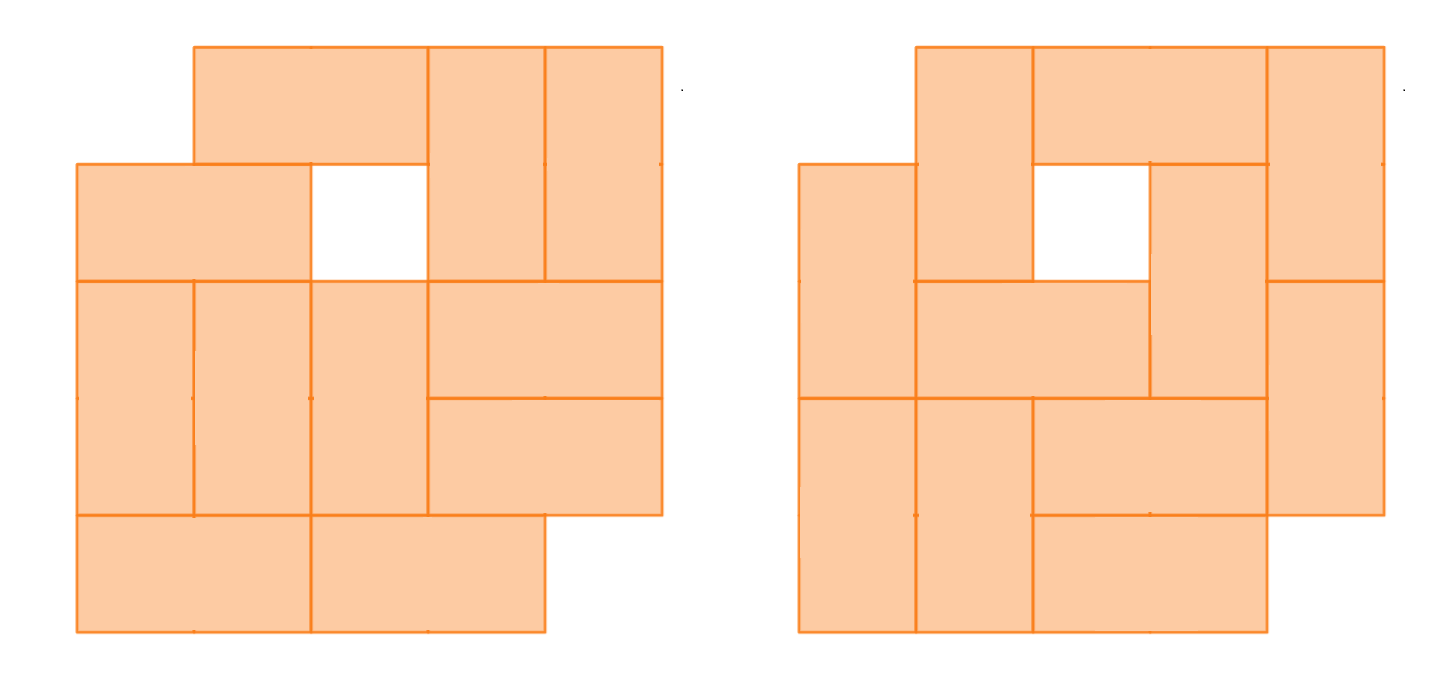ポリオミノをドミノで埋め尽くす
概要
たとえば、次のようなポリオミノをドミノで埋め尽くす方法の総数を計算するには、次のようにします。
このポリオミノをドミノで埋め尽くす方法の総数を求める
このポリオミノに対応する行列を $A$ とする。
$A$ の行列式を求める。
$\det(A)=-171745847673856$
行列式の絶対値の正の平方根を求める。
$\sqrt{|\det(A)|}=13105184$
これがドミノで埋め尽くす方法の総数と一致する。つまり
ドミノで埋め尽くす方法の総数$=13105184$
どうですか、簡単でしょう?
え?「このポリオミノに対応する行列」ってどんな行列なのか書いてない?
……わかりました。それではお見せしましょう。こんな行列になります。
対応する行列
大きすぎてすいません。実は、対応する行列のサイズはポリオミノを構成する単位正方形の数になります。上記のポリオミノは $86$ 個の単位正方形からできていますので、対応する行列は $86 \times 86$ になります。
コンピュータを使えば行列式の計算はこのサイズでも一瞬なんですけどね……。
行列の構成方法
それではここから、具体的な行列の構成方法を、次のポリオミノを例として説明していきます。
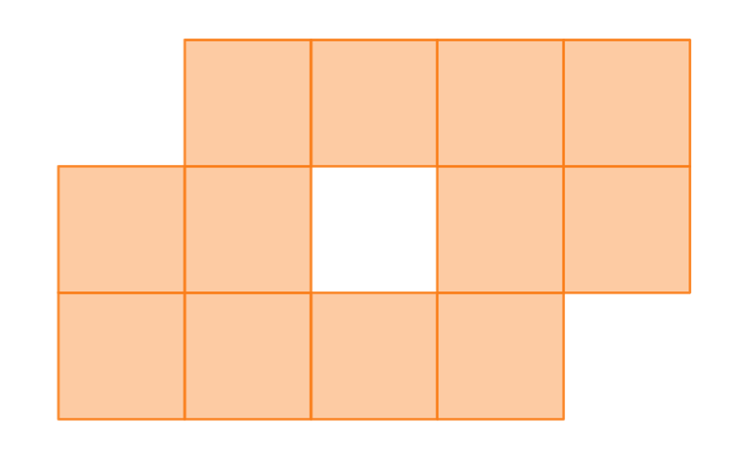このポリオミノに対応する行列を構成する
グラフを作り、頂点に番号を振る
各正方形の中心を頂点とし、隣接する頂点を辺でつないだグラフを作ります。
各頂点には「左から右、下から上」の順に番号をふって $V_1,V_2,\cdots$ と名前を付けます。
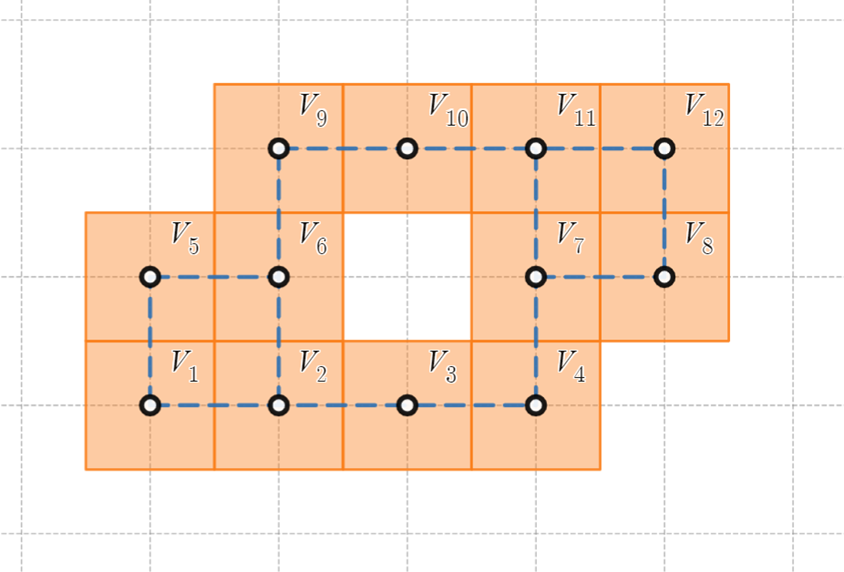グラフを作り、頂点に番号を振る
それぞれの辺に「重み」を設定する
次に、それぞれの辺に「重み」を設定します。
ヨコの辺は重みを $1$ に、タテの辺は重みを虚数単位 $i$ にします。
ただし、穴が開いていた場合は、穴と外側をつなぐ線を引いて、その線をまたぐ辺の符号を逆にします。
※ 穴と外側をつなぐ線を引く場合に、グラフの頂点を通らないようにひいてください。
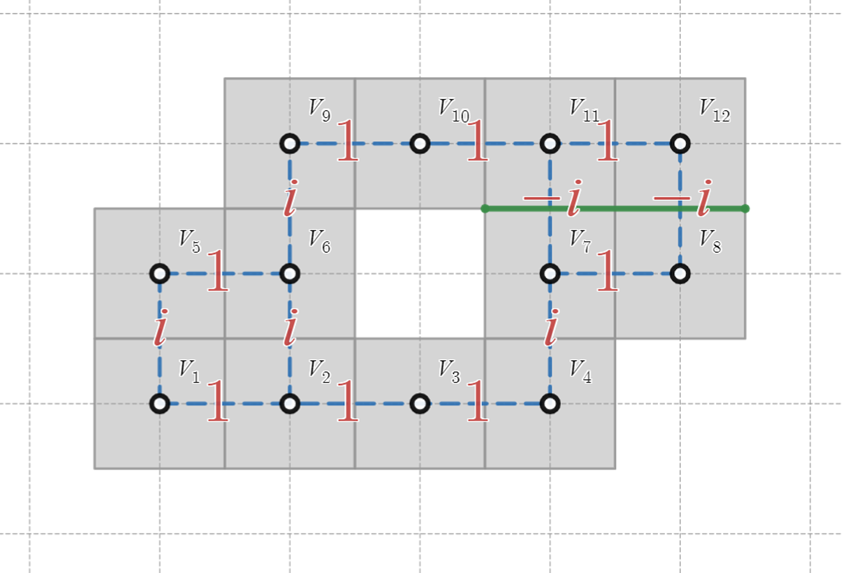辺に重みをつける
※ 図は穴が $1$ つだけの場合です。穴が $2$ つ以上ある場合については後ほど説明します。
※ 穴と外側をつなぐ線は、図 $7$ では穴の右側に引いていますが、本質的にはどの向きに引いても構いません。
頂点間の辺の重みを表にする
頂点間の辺の重みを表にします。ただし、右から左、上から下は -1 倍にします。
$\begin{array}{c|r:r:r:r:r:r:r:r:r:r:r:r:r:r:r:} 頂点番号 & V_{1} & V_{2} & V_{3} & V_{4} & V_{5} & V_{6} & V_{7} & V_{8} & V_{9} & V_{10} & V_{11} & V_{12} \\ \hline V_{1} & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hdashline V_{2} & -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 \\ \hdashline V_{3} & 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hdashline V_{4} & 0 & 0 & -1 & 0 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 \\ \hdashline V_{5} & -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hdashline V_{6} & 0 & -i & 0 & 0 & -1 & 0 & 0 & 0 & i & 0 & 0 & 0 \\ \hdashline V_{7} & 0 & 0 & 0 & -i & 0 & 0 & 0 & 1 & 0 & 0 & -i & 0 \\ \hdashline V_{8} & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & -i \\ \hdashline V_{9} & 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & 0 & 1 & 0 & 0 \\ \hdashline V_{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 1 & 0 \\ \hdashline V_{11} & 0 & 0 & 0 & 0 & 0 & 0 & i & 0 & 0 & -1 & 0 & 1 \\ \hdashline V_{12} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & i & 0 & 0 & -1 & 0 \\ \hdashline \end{array}$
※ この表はグラフ理論でいうところの「隣接行列」の一種と解釈できます。……が、特にそのことはこの記事では使いませんので気にしなくても良いです。
行列の構成
頂点間の辺の重みの表が、そのまま先ほどのポリオミノに対応する行列になります!簡単ですね!
あとは、行列式を計算し、その絶対値の正の平方根を計算すればドミノ埋め尽くしの総数が求められます!
$A=\begin{pmatrix} 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 \\ -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -i & 0 & 0 & -1 & 0 & 0 & 0 & i & 0 & 0 & 0 \\ 0 & 0 & 0 & -i & 0 & 0 & 0 & 1 & 0 & 0 & -i & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & -i \\ 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & i & 0 & 0 & -1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & i & 0 & 0 & -1 & 0 \\ \end{pmatrix}$
$\det(A)=25$
$\sqrt{|\det(A)|}=5$
ドミノ埋め尽くしの総数は $5$ とおり
複数の穴が開いている場合
複数の穴が開いている場合も、穴が1つだけのときのやり方を繰り返して辺の重みを決定すればよいです。
それぞれの穴と外側をつなぐ線を引き、その線をまたぐごとに辺の重みを -1 倍にします。複数の線をまたぐ辺は、奇数本の線をまたいだときだけ-1 倍することになります(左図)。
「重なった線を消す」ことにしても同じことです。そうすると、「穴どおしをつないだ線でもよい」ルールとも解釈できます(右図)。
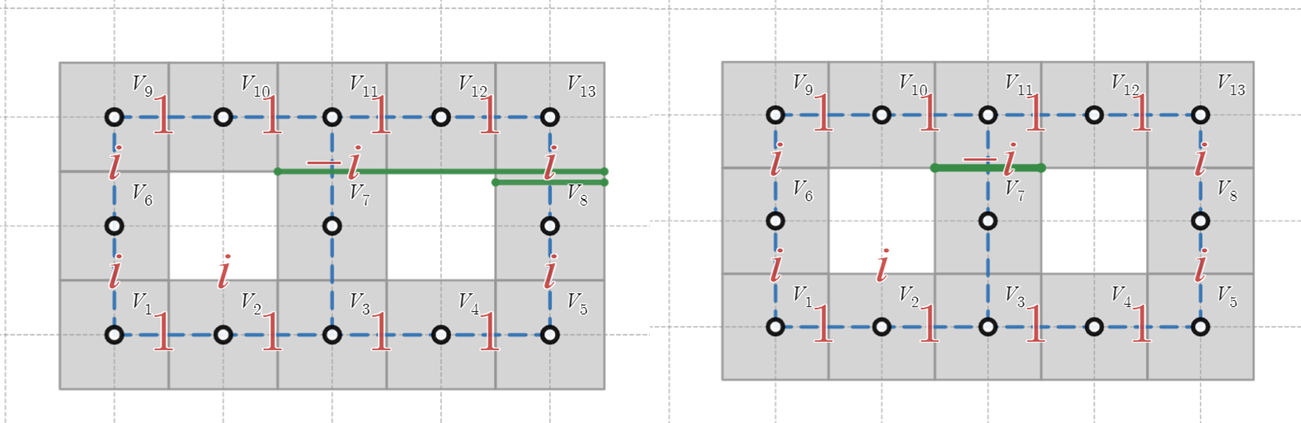複数の穴が開いている場合
穴が接している場合でも、接していない場合と同様に考えれば良いです。
そうすると、偶数個の穴が接している場合は、偶数本の線を外側とつなぐことになるので、重なるように線を引けば、結局は線を引かない事と同じになります。奇数個の穴が接している場合には $1$ 本の線を外側とつなげばよいことになります。
機械的に構成する方法
プログラムを組んで機械的に処理するならば、「タテの辺の下側の頂点の左側に空いている穴の数が奇数のときは、その辺の重みを $-1$ 倍にする」というルールで処理すれば簡単です。
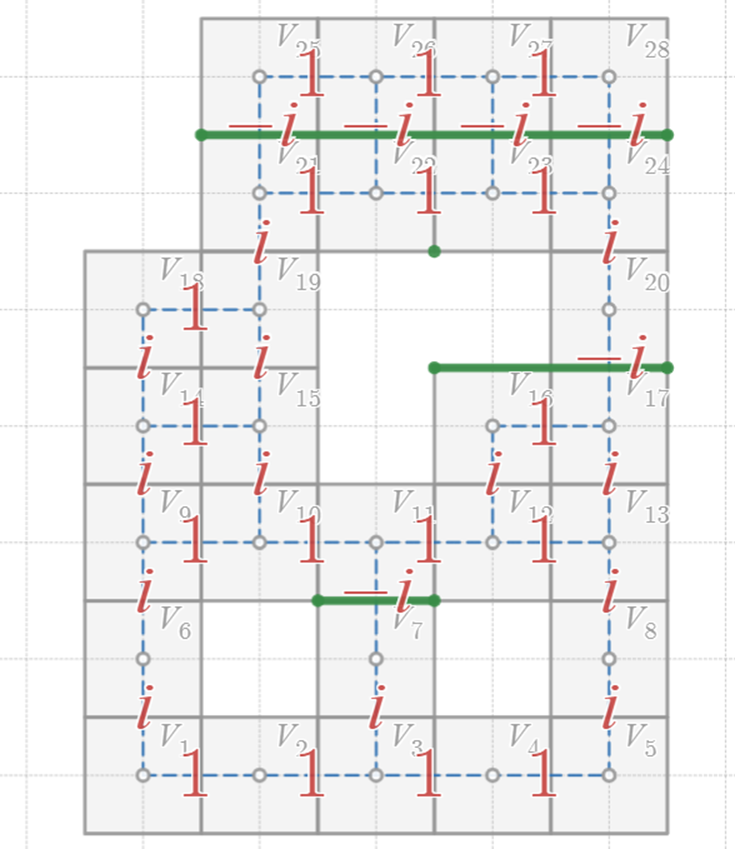機械的に構成する方法
図 $9$ で一番上の緑色の線は、プログラムで機械的に処理すると、この位置にも線が引かれることになることを表しています。なくてもいい線ですが、あっても問題ありません。
c++
参考として、c++ でのサンプルコードを載せておきます。
#include <bits/stdc++.h>
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
typedef long long ll;
int main() {
// 任意のポリオミノをドミノで埋め尽くす方法を行列式を使って求める方法
// by @apu_yokai
// double の精度で計算しているため、頂点数が多くなると誤差がでてきます。
// 盤面の配置
// '#' が配置可能場所
// '.' が配置不可能場所
// 必ず全体を長方形状にすること
vector<string> strmap = {
".####",
".####",
"##..#",
"##.##",
"#####",
"#.#.#",
"#####"
};
vector<vector<int>> map(strmap.size(),vector<int>(strmap.at(0).length()));
for (int i = 0; i < strmap.size(); i++){
// 文字列を一文字ずつ調べて0または1を設定
for (int j = 0; j < strmap.at(i).length(); j++) {
if (strmap.at(i)[j] == '.') {
map.at(i).at(j) = 0;
} else if (strmap.at(i)[j] == '#') {
map.at(i).at(j) = 1;
} else {
// それ以外の文字に対する処理（必要に応じて追加）
}
}
}
int m = map.size();
int n = map.at(0).size();
vector<pair<ll, ll>> V={}; // 頂点を入れる配列
vector<ll> parity={}; // 頂点の左側にある「穴」の数のパリティ 1...even -1...odd
for (int i = m; i >= 1; i--) {
int pm = 1;
for(int j = 1; j <= n; j++) {
if (map.at(i - 1).at(j - 1) == 1) {
V.push_back(make_pair(m + 1 - i,j));
parity.push_back(pm);
} else {
pm = -pm;
}
}
}
// 複素行列の宣言
MatrixXcd complexMatrix(V.size(), V.size());
for (int ii = 0; ii < V.size(); ii++) {
for (int jj = 0; jj < V.size(); jj++) {
int i = V.at(ii).first;
int j = V.at(ii).second;
int k = V.at(jj).first;
int l = V.at(jj).second;
// ここから隣接行列の成分を作成
// parity が -1 のときは縦方向を -1倍にしている
if ( k == i && l == j - 1) {cout << "-1 "; complexMatrix(ii, jj) = complex<double>(-1.0, 0.0);}
else if (k == i && l == j + 1) {cout << "1 "; complexMatrix(ii, jj) = complex<double>(1.0, 0.0);}
else if (k == i + 1 && l == j) {if (parity.at(ii) == 1) {cout << "i "; complexMatrix(ii, jj) = complex<double>(0.0, 1.0);}
else {cout << "-i "; complexMatrix(ii, jj) = complex<double>(0.0, -1.0);}}
else if (k == i - 1 && l == j) {if (parity.at(jj) == 1) {cout << "-i "; complexMatrix(ii, jj) = complex<double>(0.0, -1.0);}
else {cout << "i "; complexMatrix(ii, jj) = complex<double>(0.0, 1.0);}}
else { cout << "0 "; complexMatrix(ii, jj) = complex<double>(0.0, 0.0);}
}
cout << endl;
}
// 行列式を計算し、実部を取り出す(虚部はゼロになる)
double det = complexMatrix.determinant().real();
// ドミノタイリングの総数を計算する。
double Z = sqrt(abs(det));
// 出力の精度を設定
cout << setprecision(15); // 15桁の精度
// 結果を出力
cout << "行列式の値: " << det << endl;
cout << "ドミノタイリングの総数: " << Z << endl;
return 0;
}
このコードは、ポリオミノに対応する行列と行列式とドミノタイリングの総数を出力します。
出力された行列は、コピーして行列式計算サイトへペーストすることで行列式を計算することができます。
外部サイト： Matric Calculator 行列計算機
なぜこの方法でうまくいくのか
なぜ「穴と外側をつなぐ線をまたぐ辺の重みを -1 倍にする」とうまくいくかというと、交互閉路の回転による切り替えで頂点の置換のパリティと辺の重みの積のパリティが連動するようになるからです。
ドミノタイリングの数え上げ公式の導出方法【後編～証明～】 の最後の部分を思い出してください。
長方形のポリオミノをドミノで敷き詰める場合に、交互閉路の回転により相互に移る配置で、対応する行列のパフィアンの計算での置換の符号の交代がキャンセルされる証明の流れは次のようなものでした。
$[1]$ 辺の重みの総積のパリティと交互閉路内の単位正方形の数のパリティは連動する。
$\mathcal{E}^{[A]} \cdot (-1)^{S}=\mathcal{E}^{[B]}$
$[2]$ 置換のパリティと交互閉路上の頂点数のパリティは連動する。
$\operatorname{sgn}(\sigma^{[A]})=(-1)^{V_e-1}\cdot{\operatorname{sgn}(\sigma^{[B]})}$
$[3]$ 辺々掛け合わせて次の式を得る。
${\operatorname{sgn}(\sigma^{[A]})}\cdot\mathcal{E}^{[A]} \cdot(-1)^{S-V_e+1}={\operatorname{sgn}(\sigma^{[B]})}\cdot\mathcal{E}^{[B]} $
$[4]$ ピックの定理より、交互閉路内の頂点数 $V_i=S-V_e+1$ であるから
${\operatorname{sgn}(\sigma^{[A]})}\cdot\mathcal{E}^{[A]} \cdot(-1)^{V_i}={\operatorname{sgn}(\sigma^{[B]})}\cdot\mathcal{E}^{[B]} $
$[5]$ 交互閉路の内側にある頂点も必ずペアにならなければならないから $V_i$ は偶数である。したがって
$(-1)^{V_i}=1$
$[6]$ 置換のパリティと辺の重みの総積のパリティは連動する。すなわち置換による符号の交代がキャンセルされる。
${\operatorname{sgn}(\sigma^{[A]})}\mathcal{E}^{[A]}={\operatorname{sgn}(\sigma^{[B]})}\mathcal{E}^{[B]}$
一般のポリオミノの場合も、「ポリオミノに穴が開いていない場合は」この長方形の敷き詰めの場合の考え方がそのまま使えます。
お恥ずかしい話ですが、実は当初、私は一般のポリオミノの場合も、全く同じ方法でドミノ埋め尽くしの総数を求められるのではないかと考えていました……が、実際に検証してみた結果、計算が合わなかったため、ポリオミノに穴が開いている場合にはそのままでは使えないことに気が付きました。
そのときのポストたち
ちょっと検証したいことがあって協力してほしいんですが、この2つの盤面それぞれについて、ドミノタイリング(1×2の長方形の敷き詰め)の方法の総数がいくらになるか数えてもらえませんか? pic.twitter.com/n2AnWJzgoh
— ａｐｕ (@apu_yokai) October 25, 2023
検証していただいた結果、ある予想が外れていたことがわかった(無念)
— ａｐｕ (@apu_yokai) October 25, 2023
ぐぬぬ
では、何が問題だったのでしょうか。
結論としては、 「$[5]$ 交互閉路の内側にある頂点も必ずペアにならなければならないから $V_i$ は偶数である。」 の部分に問題がありました。交互閉路内に穴が開いている場合は、穴の数も計算に含める必要があったのです!
交互閉路内の格子点で頂点がない点を「穴」とし、穴の数を $H$ で表すことにします。すると、さきほどの流れはこのように修正できます。
$[1]$ 辺の重みの総積のパリティと交互閉路内の単位正方形の数のパリティは連動する。
$\mathcal{E}^{[A]} \cdot (-1)^{S}=\mathcal{E}^{[B]}$
$[2]$ 置換のパリティと交互閉路上の頂点数のパリティは連動する。
$\operatorname{sgn}(\sigma^{[A]})=(-1)^{V_e-1}\cdot{\operatorname{sgn}(\sigma^{[B]})}$
$[3]$ 辺々掛け合わせて次の式を得る。
${\operatorname{sgn}(\sigma^{[A]})}\cdot\mathcal{E}^{[A]} \cdot(-1)^{S-V_e+1}={\operatorname{sgn}(\sigma^{[B]})}\cdot\mathcal{E}^{[B]} $
$[4]$ ピックの定理より、交互閉路内の頂点数と穴の数の和 $V_i\textcolor{red}{+H}=S-V_e+1$ であるから
${\operatorname{sgn}(\sigma^{[A]})}\cdot\mathcal{E}^{[A]} \cdot(-1)^{V_i\textcolor{red}{+H}}={\operatorname{sgn}(\sigma^{[B]})}\cdot\mathcal{E}^{[B]} $
$[5]$ 交互閉路の内側にある頂点も必ずペアにならなければならないから $V_i$ は偶数である。したがって
$(-1)^{V_i\textcolor{red}{+H}}=\textcolor{red}{(-1)^{H}}$
$[6]$ 置換のパリティと辺の重みの総積のパリティは交互閉路内の穴の数が奇数のときは逆になる。
${\operatorname{sgn}(\sigma^{[A]})}\mathcal{E}^{[A]}\textcolor{red}{\cdot(-1)^{H}}={\operatorname{sgn}(\sigma^{[B]})}\mathcal{E}^{[B]}$
気が付いてしまえば単純な話でしたので、修正は容易でした。
要するに、穴が開いている場合には、交互閉路を構成する辺を $1$ つ選んで重みの符号を逆にしてやればよいのです。そうすれば、回転したときに辺の重みの積が $-1$ 倍されて、置換の符号の交代をキャンセルすることができます。
そして、符号を逆にする辺を選ぶためには、穴と外側をつなぐ線を引いて、それをまたぐ辺を選べばよいのです!
こうして、実にシンプルなアルゴリズムが完成したのでした!
めでたしめでたし。
神ゲーム「ドミノタイリングの数え上げ」の誕生
それから、このゲームを紹介しないわけにはいきません。
検証の過程で、Tatt（たっと）@tatt61880 さんに、ドミノタイリングの数え上げをテーマにしたゲームを作っていただきました!
"ドミノタイリングの数え上げ"https://t.co/cQHPWsBW70
— Tatt（たっと） (@tatt61880) November 1, 2023
最大7x6の盤面に関してドミノタイリングの総数を一瞬で求めるサイトを公開しています。
自動的にコレクションする機能もあります。
目指せ、ドミノタイリングマスター！ pic.twitter.com/Lj1OXQeygw
・
ドミノタイリングの数え上げ
ゲーム画面
このゲームは私がアルゴリズムの検証をするのに大いに役立っただけではなく、コレクション機能が追加されたことにより、純粋にゲームとしても非常に中毒性の高いゲームになっています。是非遊んでみて、沼にはまって欲しいと思います。
おわりに
というわけで、ポリオミノをドミノで埋め尽くす方法の総数を、行列式を使って「機械的に」「あっという間に」計算できる、私が考案したアルゴリズムをご紹介しました。
とは言っても、「ポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求めることが可能である」こと自体はカステレインなどの数学者が既に考案・証明しています。
また、「あっという間に」というのは行列式は多項式時間で解ける問題である($n$ 次正方行列の行列式の計算のオーダーは $O(n^3)$ であることが知られています。)であることを表現したもので、これも私のアイデアで高速化したというわけではありません。
私が考案したのは、この問題を解くための行列を「機械的に」構築する方法の部分です。つまり、この記事の前半部分で説明した部分です。
手前味噌ですが、実にシンプルなルールで行列を構築できたと思っています。
それから、日曜数学会のスライドを作ってて思ったんですが、これってものすごく「競プロ」み がありますよね。 もしかして競プロでこんな出題があったりしたのでしょうか。 もしあった場合、想定解法はこんな感じだったのでしょうか。 情報があれば教えて欲しいです!
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
