ドミノタイリングの数え上げ公式の導出方法【前編～導出～】

はじめに

　この記事では、$m \times n$ の長方形をドミノタイリングする方法が何通りあるかを計算する公式について考察します。

　まず、「ドミノタイリング」について説明します。
　ドミノタイリングというのは、図$1$ のようにしてドミノ($1 \times 2$ の長方形)で領域を埋めつくすことをいいます。

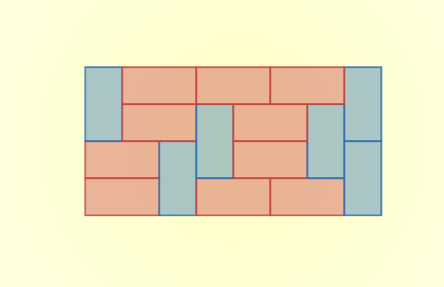ドミノタイリングの例

　この、ドミノタイリングの方法が何通りあるかを考えるわけです。なお、回転したり裏返したりして重なるものについても異なるものとして数えます。

　記事を【前編～導出～】と【後編～証明～】にわけています。

　前編では、公式の導出までを一気に解説します。ただし、一部の説明は省略しています。
　後編では、省略した部分を補足して、なぜこの公式がドミノタイリングの総数となるのかについて掘り下げたいと思います。

　なお、導出方法は参考文献の「線形代数と数え上げ[増補版]」を大いに参考にしていますが、一部に私の独自の改変が加えてあります。致命的なミスはないと信じていますが、問題があれば優しく教えていただければ幸いです。

(R5.10.21　後編を公開しました!)
リンク: Mathlog|ドミノタイリングの数え上げ公式の導出方法【後編～証明～】

(R5.11.4　応用編となる記事を公開しました!)
リンク: Mathlog|任意のポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求める方法(日曜数学会)

観察

　$m \times n$ の長方形のドミノタイリングの方法の数を $Z_{m,n}$ とあらわすことにします。

　手始めに、小さいときから考えてみましょう。
　総当たりで調べると $Z_{1,2}=1,Z_{2,2}=2,Z_{2,3}=3,Z_{3,4}=11$ となります。
　
$Z_{3,4}=11$

$m,n$ が $10$ 以下の場合の $Z_{m,n}$ の値について表にすると、次のようになります。

$\begin{array}{c|r:r:r:r:r:r:r:r:r:r:} m\backslash n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline 1 & 0 & 1 & 0 & 1 & 0 & 1& 0 & 1& 0 & 1 \\ \hdashline 2 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55& 89 \\ \hdashline 3 & 0 & 3 & 0 & 11 & 0 & 41 & 0 & 153 & 0 & 571\\ \hdashline 4 & 1 & 5 & 11 & 36 & 95 & 281 & 781 & 2245 & 6336 & 18061\\ \hdashline 5 & 0 & 8 & 0 & 95 & 0 & 1183 & 0 & 14824 & 0 & 185921\\ \hdashline 6 & 1 & 13 & 41 & 281 & 1183 & 6728 & 31529 & 167089 & 817991 & 4213133\\ \hdashline 7 & 0 & 21 & 0 & 781 & 0 & 31529 & 0 & 129{}2697 & 0 & 53175517\\ \hdashline 8 & 1 & 34 & 153 & 2245 & 14824 & 167089 & 129{}2697 & 12988816 & 108435745 & 103{}1151241\\ \hdashline 9 & 0 & 55 & 0 & 6336 & 0 & 817991 & 0 & 108435745 & 0 & 144{}79521761\\ \hdashline 10 & 1 & 89 & 571 & 18061 & 185921 & 4213133 & 53175517 & 103{}1151241 & 144{}79521761 & 258584046368\\ \hdashline \end{array} $

　この表を見ているだけでもわかることがいくつかありますので、本題に入る前に、この表を観察してみましょう。

　まず、$m,n$ がともに奇数の場合は $0$ になっていますね。
　$m,n$ がともに奇数の場合は、長方形の面積が奇数になるので、ドミノで敷き詰めることが不可能なので $0$ というわけですね。

　それから、$m,n$ の片方が $1$ の場合は、直線状に並べるしかないので $0$ と $1$ が交互に並んでいます。

　$m,n$ の片方が $2$ の場合はどこかでみた数列になっていますね。
　そう、フィボナッチ数列です!
　この記事ではこれ以上説明しませんが、本当にフィボナッチ数列であることを証明することができます。

　$m,n$ がともに $3$ 以上の場合については、簡単な法則はなさそうに見えます。

　それから、全体の傾向として、(両方が奇数の場合を除いて、)$m,n$ が大きくなるにつれて場合の数が爆発的に大きくなっています。いわゆる「組み合わせ爆発」が起きていますね。

　ちなみに、 $m=n=20$ の場合、実に

$Z_{20,20}=1269984011256235834242602753102293934298576249856$

　という数になります!
　読み方は「1 極 2699 載 8401 正 1256 澗 2358 溝 3424 穣 2602 秭 7531 垓 229 京 3934 兆 2985 億 7624 万 9856」です。

　仮に総当たりでこれを数え上げようとするならば、$1$ 秒間に $1$ 京とおりを調べることができたとしても $4.0\times10^{24}$ 年以上かかります。宇宙の寿命が先に尽きてしまいます。

　これほどの数になると、たとえスーパーコンピュータを使ったとしても、まともに数え上げることはできそうもありません。・・・が、実は一つ一つ調べることなくその総数を計算できる公式があるのです。(だから上記の数がわかるわけですが)

　それでは、その公式をご紹介しましょう。こんな公式です。

　「公式に出てくる記号の意味がわからない!」という方はこちらをご覧ください。

　記号の意味を説明したところで、もう一度公式を見てみましょう。

　${\displaystyle 　\prod_{j=1}^{\left\lceil\frac{m}{2} \right\rceil}\prod_{k=1}^{\left\lceil\frac{n}{2} \right\rceil} 　\left( 　4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1} 　\right)}$
　
　計算の仕方はわかりますが、それにしても、式の中に $\cos$ が出てくるのが不思議だと思いませんか?

　試しに $m=3,n=4$ で計算してみると

　計算途中には無理数も出てきますが、最終的な計算結果は整数になりました。さきほどの表の値と同じ $11$ になりましたね!

　また、$m,n$ がともに奇数の場合は、総積の中にゼロとなる項があるのでゼロになることが分かります。 　

Desmos：検算用

公式の導出

　いやあ、それにしても凄い式です。組み合わせ爆発でとんでもないことになる場合の数を一瞬で計算できてしまうのですから。

　そんなわけで、まずはこの公式を導出しましょう。途中で気になるところがいろいろ出てくるとは思いますが、まずはスピード重視で計算を進めます。

手順 $1$　複素数平面上に長方形を配置する

　$m\times n$ の長方形を構成する各単位正方形の中心を頂点とするグラフを考えます。頂点を結ぶ辺は、頂点に対応する単位正方形が隣接している場合に引きます。
　
　そして、そのグラフを、複素数平面の格子点に頂点が重なるように配置します。

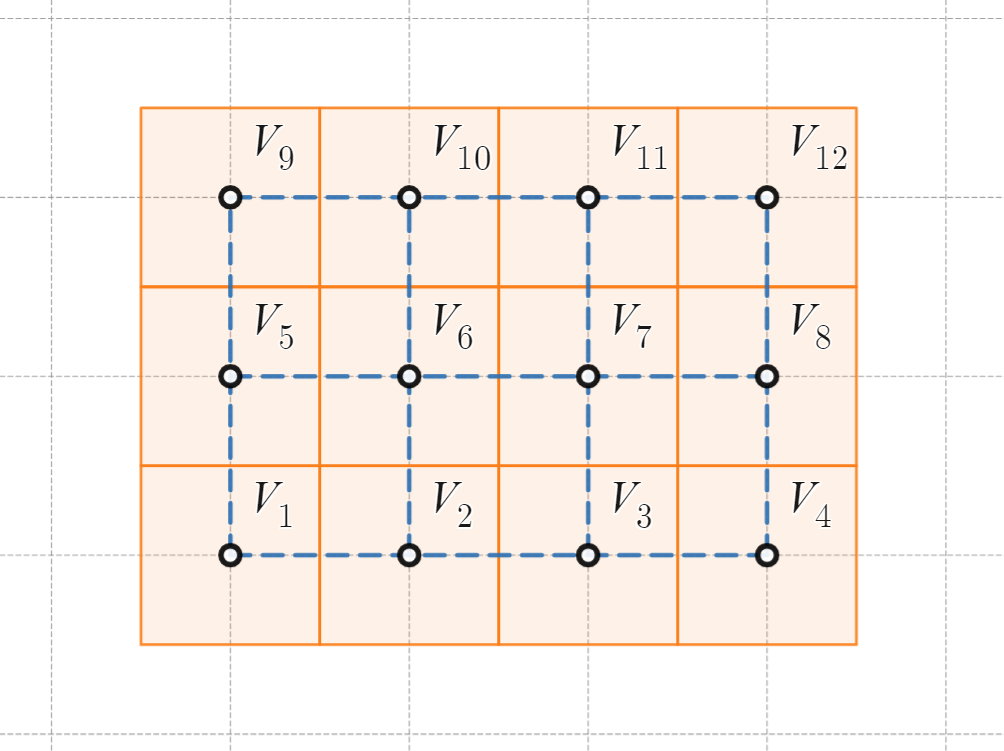単位正方形の中心を複素数平面の格子点と重なるように配置

　$m\times n$ の長方形には $mn$ 個の頂点があります。
　頂点には図のように番号をふります。
　すなわち、左下を $V_1$ として、実軸方向に $1$ ずつ番号を増やしていき、虚軸方向には $n$ ずつ番号を増やしていきます。

　下から $j$ 番目、左から $k$ 番目の頂点は $V_{n(j-1)+k}$ というわけです。

　これらの頂点の隣接関係を表にします。

手順 $2$　行列を作り、行列式を計算する

　頂点が隣接していない場合は $0$ を、隣接している場合は次の図のように、隣の頂点との差分を表に書き込んでいきます。

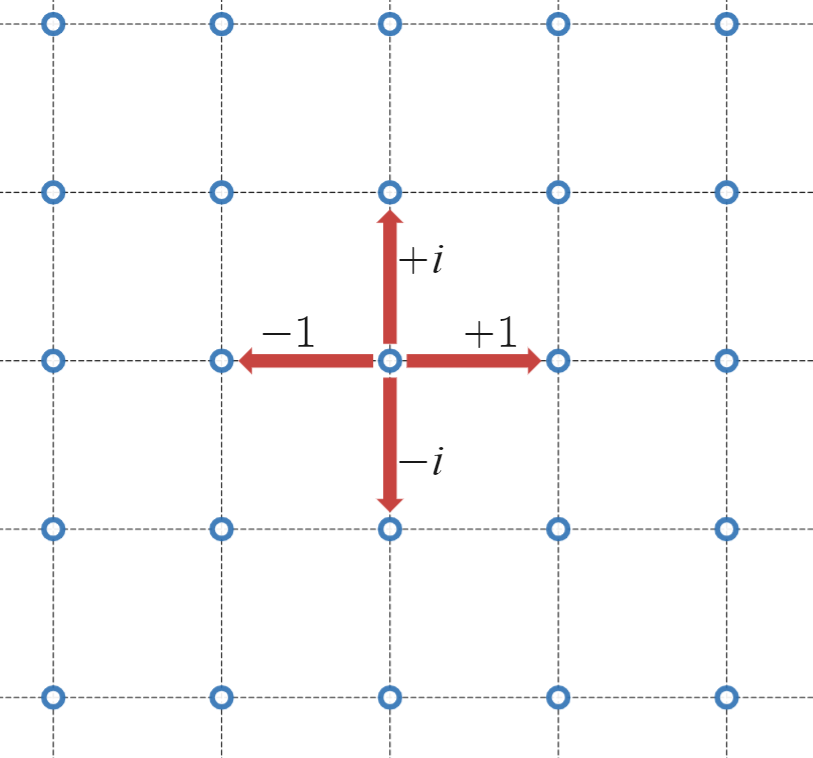隣の頂点との差分

　「表の $j$ 行 $k$ 列目の成分は $V_j$ と $V_k$ の位置の差分(ただし隣接していない場合は $0$)」として頂点の隣接関係を表にするとこんな感じの表ができます。

　なお、具体的な数字を入れた方が分かりやすいと思いますので、ここからは $m=3,n=4$ の場合について計算を進めます。

　これを $12$ 次正方行列とみて、行列式を計算します。
　(余談ですが、このような行列を「隣接行列」と呼んだりします。グラフ理論とも関係がありますが、ここでは深入りしません。)
　
　手作業では大変なので、計算サイトなどを利用して行列式を計算すると、$121$になります。

利用したサイト： Matrix calculator 行列式計算機

$\begin{vmatrix} 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 0 & 0 & i & 0 & 0 & 0 & 0 \\ -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 \\ 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 & 0 & i & 0 & 0 \\ 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 & 0 & i & 0 \\ 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 0 & 0 & 0 & i \\ 0 & 0 & 0 & 0 & -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 \\ \end{vmatrix}=121$

　行列式の平方根、すなわち $\sqrt{121}=11$ が、$3\times4$ のドミノタイリングの総数と一致しています。

　これが偶然ではないことを確かめるために、$10$ 以下の $m,n$ について行列式を計算したものを表にしてみました。

$\begin{array}{c|r:r:r:r:r:r:r:r:r:r:} m\backslash n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ \hdashline 2 & -1 & 4 & -9 & 25 & -64 & 169& -441 & 1156 & -3025 & 7921 \\ \hdashline 3 & 0 & 9 & 0 & 121 & 0 & 1681& 0 & 23409 & 0 & 326041 \\ \hdashline 4 & 1 & 25 & 121 & 1296 & 9025 & 78961& 609961 & 5040025 & 40144896 & 326199721 \\ \hdashline 5 & 0 & 64 & 0 & 9025 & 0 & 139{}9489 & 0 & 219750976& 0 & 345{}66618241 \\ \hdashline 6 & -1 & 169 & -1681 & 78961 & -1399489 & 45265984 & -994077841 & 279{}18733921 & -669109276081 & 177{}50489675689 \\ \hdashline 7 & 0 & 441 & 0 & 609961 & 0 & 994077841& 0 & 167{}1065533809 & 0 & 282{}7635608217289 \\ \hdashline 8 & 1 & 1156 & 23409 & 5040025 & 219750976 & 27918733921& 167{}1065533809 & 168{}709341081856 & 117{}58310793705025 & 1063272881815840081 \\ \hdashline 9 & 0 & 3025 & 0 & 40144896 & 0 & 669109276081& 0 & 117{}58310793705025 & 0 & 209656550427272541121 \\ \hdashline 10 & -1 & 7921 & -326041 & 326199721 & -34566618241 & 177{}50489675689 & -2827635608217289 & 1063272881815840081 & -209656550427272541121 & 66865709036047973991424 \\ \hdashline \end{array} $

　この表と、冒頭の$m,n$ が $10$ 以下の場合のドミノタイリングの総数の表を見比べてみてください。
　ドミノタイリングの総数を $Z_{m,n}$ とし、この表の行列式を $\det(A)$ とすると、次の関係が見えてきます。

　ドミノタイリングの総数が、行列式の絶対値の平方根と一致しています。
　このことを利用して、公式を導出することができます。

手順 $3$　行列の固有値と固有ベクトル

　ところで、サイズの大きな行列式の計算を定義通りに計算すると、組み合わせ爆発になってしまい大変です。そこで、簡単に計算できる方法がいろいろ研究されています。今回は、行列の固有値を使って簡単に行列式を計算していきます。

　$m \times n$ の長方形に対応する行列は、$mn$ 行 $mn$ 列の行列でした。

　固有値と固有ベクトルの組は $mn$ 組あります。この後の説明をやりやすくするために、添え字を $2$ 種類にします。

　イメージとしては、グラフの頂点 $V_{n(j-1)+k}$ それぞれに固有値 $\lambda_{j,k}$ と固有ベクトル $\phi_{j,k}$ を対応させたものと考えるとよいでしょう。

　固有ベクトルにはそれぞれ $mn$ 個の成分がありますから、これにも添え字を $2$ 種類つけて、固有ベクトル $\phi_{j,k}$ の成分を $\varphi_{s,t}^{(j,k)}$ のようにあらわすことにしましょう。ただし、添え字が多すぎると見づらいので、適宜 $\varphi_{s,t}$ のように添え字の一部を省略して書くことにします。

　さて、じつに天下り的ですが、今考えている行列の固有値と固有ベクトルの成分はこんなふうに書くことができます。

　これらの固有値・固有ベクトルは、$m,n$ を色々変えて実際に固有値・固有ベクトルを計算してみると、なんとなく法則性があることから推測して見つけることができます。

利用したサイト： Matrix calculator 固有値計算機

　「推測した固有値なんて怪しい」ですって?
　ごもっともです。本当に固有値・固有ベクトルなのか、定義にしたがって検算して確認しておきましょう。
　本当は微分方程式の類似として差分方程式を変数分離法で解くことでも求められるらしいけど私にはわかりませんでした。

　ではさきほど「固有値」「固有ベクトル」としてあげた式たちが本当に定義を満たしているのか検算して確認してみましょう。
　$A$ を $\phi_{j,k}$ に作用させたベクトルを $\Psi_{j,k}$ であらわすことにします。つまり $(\Psi_{j,k}=A\,\phi_{j,k})$
　$\Psi$ の成分を $\psi$ で、次のようにあらわすことにします。

　このとき、$\psi$ は $\varphi$ を使って次の式で表すことができます。

　ただし、$\varphi$ の添え字が範囲外になるときは $0$ として計算します。

　…さらっと書きましたが、ここは結構な驚きポイントだと思いますので、本当にこの関係が成り立つのか、ちょっと確かめてみましょう。

　行列の成分をみると、$-i,-1,1,i$ が左上から右下へ直線状にならんでいます。

$\begin{pmatrix} 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0 & 0 & 0 & i & 0 & 0 & 0 & 0 \\ -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 & i & 0 & 0 & 0 \\ 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 & 0 & i & 0 & 0 \\ 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 & 0 & i & 0 \\ 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 0 & 0 & 0 & i \\ 0 & 0 & 0 & 0 & -i & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -i & 0 & 0 & -1 & 0 \\ \end{pmatrix}$

　そのことを利用して、先ほどの式(☆)ができていたわけです。

　・・・が、よくみると、$-1$ と $1$ は直線状の並びの一部が途切れています。長方形の端の位置、すなわち $t=1$ のときには $-1$ が途切れて、$t=n$ のときは $1$ が途切れています。
　そのときでも、先ほどの式(☆)は成立します。

　なぜなら、$t=1$ のときは

　　$\varphi_{s,t-1}=i^{t+1-s}\sin\frac{\pi js}{m+1}\cdot\underbrace{\sin\frac{\pi k(1-1)}{n+1}}_{=0}$

　がゼロになり、$t=n$ のときも

　　$\varphi_{s,t+1}=i^{t+1-s}\sin\frac{\pi js}{m+1}\cdot\underbrace{\sin\frac{\pi k(n+1)}{n+1}}_{=0}$

　がゼロになり、うまいことつじつまが合うのです!

　それでは、
　$\varphi_{s,t}^{(j,k)}=i^{t-s}\sin\frac{\pi js}{m+1}\cdot\sin\frac{\pi kt}{n+1}$
　を先ほどの式(☆)に代入して計算を進めてみましょう。

　${\displaystyle \begin{align} \psi_{s,t}&=-i\varphi_{s-1,t}-\varphi_{s,t-1}+\varphi_{s,t+1}+i\varphi_{s+1,t}\\ &=-i\cdot i^{t-(s-1)}\sin\frac{\pi j(s-1)}{m+1}\cdot\sin\frac{\pi kt}{n+1}-i^{(t-1)-s}\sin\frac{\pi js}{m+1}\cdot\sin\frac{\pi k(t-1)}{n+1}\\ &\qquad +i^{(t+1)-s}\sin\frac{\pi js}{m+1}\cdot\sin\frac{\pi k(t+1)}{n+1}+i\cdot i^{t-(s+1)}\sin\frac{\pi j(s+1)}{m+1}\cdot\sin\frac{\pi kt}{n+1}\\ &=i^{t-s}\sin\frac{\pi kt}{n+1}\left(\sin\frac{\pi j(s-1)}{m+1}+\sin\frac{\pi j(s+1)}{m+1}\right)\\ &\qquad +i\cdot i^{t-s}\sin\frac{\pi js}{m+1}\left(\sin\frac{\pi k(t-1)}{n+1}+\sin\frac{\pi k(t+1)}{n+1}\right)\\ &=i^{t-s}\sin\frac{\pi kt}{n+1}\cdot 2\sin\frac{\pi js}{m+1}\cos\frac{\pi j}{m+1}\\ &\qquad +i\cdot i^{t-s}\sin\frac{\pi js}{m+1}\cdot 2\sin\frac{\pi kt}{n+1}\cos\frac{\pi k}{n+1}\\ &=\left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\cdot i^{t-s}\sin\frac{\pi js}{m+1}\sin\frac{\pi kt}{n+1}\\ &=\lambda_{j,k}\,\varphi_{s,t} \end{align} }$

　${\psi_{s,t}}$ は ${\Psi_{j,k}}$ の成分で、${\varphi_{s,t}^{(j,k)}}$ は ${\phi_{j,k}}$ の成分なので

$\Psi_{j,k}=A\,\phi_{j,k}$ ですから

というわけで、$\lambda_{j,k}$ と $\phi_{j,k}$ は、確かに固有値と固有ベクトルの定義を満たしています。

手順 $4$　固有値の積で行列式を計算する

　行列式の値は全ての固有値の積と一致します。

　この性質を使って行列式を求めましょう。
　$m\times n$ のドミノタイリングに対応する $mn$ 次正方行列を $A_{m,n}$ とします。
　先に書いた通り、行列 $A_{m,n}$ に対応する固有値は

　　$\lambda_{j,k}=2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}$ 　　

です。$j,k$ は $ 1\le j \le m,\,1\le k \le n $　の範囲を動きますので、固有値は $mn$ 個あります。

求める行列式を $\det(A_{m,n})$ と書きます。

　${\displaystyle \begin{align} \det(A_{m,n})&=\prod_{j=1}^{m}\prod_{k=1}^{n} \lambda_{j,k} \end{align} }$

ということになります。
この式に

　$\lambda_{j,k}=2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}$

を代入することで次の式が得られます。

　$mn$ 個の固有値を複素数平面に並べると、実軸方向に $m$ 個、虚軸方向に $n$ 個の長方形状に並ぶことが分かります。対称性を利用して式をシンプルにすることを考えます。
　特に、共役複素数の積が実数になることを利用することで実数のみの式にすることができます。

　あまり場合分けはしたくないのですが、ここではやむを得ず場合分けをしましょう。
　$m,n$ の偶奇で場合分けして計算していきます。

$m$ が偶数、$n$ も偶数のとき

$A_{4,4}$ の固有値

$(m:even,n:even)$

　${\displaystyle \begin{align} \det(A_{m,n}) &=\prod_{j=1}^{m}\prod_{k=1}^{n} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\\ &=\prod_{j=1}^{m}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\\ &=\left(\prod_{j=1}^{\frac{m}{2}}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ \end{align} }$

$m$ が奇数、$n$ も奇数のとき

$(m:odd,n:odd)$

$A_{3,3}$ の固有値

　$j=\frac{m+1}{2},k=\frac{n+1}{2}$ のときカッコ内がゼロになるので総積もゼロになります。
　
　${\displaystyle \begin{align} \det(A_{m,n}) &=\prod_{j=1}^{m}\prod_{k=1}^{n} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\\ &=0\\ \end{align} }$

$m$ が奇数、$n$ は偶数のとき

$(m:odd,n:even)$

$A_{3,4}$ の固有値

　${\displaystyle \begin{align} \det(A_{m,n}) &=\prod_{j=1}^{m}\prod_{k=1}^{n} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\\ &=\prod_{j=1}^{m}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\\ &=\left(\prod_{j=1}^{\frac{m-1}{2}}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ 　　&\qquad \times 　　 \underbrace{\prod_{j=\frac{m+1}{2}}^{\frac{m+1}{2}}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)}_{=1}\\ &=\left(\prod_{j=1}^{\frac{m+1}{2}}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ \end{align} }$

　$3$ 行目から $4$ 行目の変形に注目してください。わざわざ $1$ になる項をもう一回かけています。なぜこんなことをしているかというと、あとで場合分けのない $1$ つの式に統合するときに都合がいいからです。

　また、$3$ 行目で $=1$ となっている部分。本当に $1$ になるのかあやしいと思いませんか?念の為確認しておきましょう。

　　${\displaystyle \begin{align} &\prod_{j=\frac{m+1}{2}}^{\frac{m+1}{2}}\prod_{k=1}^{\frac{n}{2}} \left(\underbrace{4\cos^2\frac{\pi j}{m+1}}_{=0}+4\cos^2\frac{\pi k}{n+1}\right)\\ &= \prod_{k=1}^{\frac{n}{2}} \left(2\cos\frac{\pi k}{n+1}\right)^2\\ &= \prod_{k=1}^{\frac{n}{2}} \left(\exp\left(\frac{i\pi k}{n+1}\right)+\exp\left(-\frac{i\pi k}{n+1}\right)\right)^2\\ &= \prod_{k=1}^{\frac{n}{2}} \left(\exp\left(\frac{i\pi k}{n+1}\right) \left( 1+\exp\left(-\frac{2i\pi k}{n+1}\right) \right) \exp\left(\frac{-i\pi k}{n+1}\right) \left( \exp\left(\frac{2i\pi k}{n+1}\right)+1 \right) \right)\\ &= \prod_{k=1}^{n} \left( \exp\left(\frac{2i\pi k}{n+1}\right)+1 \right)\\ \end{align} }$

この最後の式が $1$ になることを示すには次のようにすればよいです。

　$x^{n+1}-1=(x-1)(x^{n}+x^{n-1}+\cdots+1)$

と

　$x^{n+1}-1=(x-1)\prod_{k=1}^{n}\left( x-\exp\left(2i\pi\frac{k}{n+1}\right) \right)$

を比較して

　$\prod_{k=1}^{n}\left( x-\exp\left(2i\pi\frac{k}{n+1}\right) \right) =x^{n}+x^{n-1}+\cdots+1$

　$x=-1$ を代入し、$n$ が偶数であることに注意して計算すると

　$\begin{align} 　\prod_{k=1}^{n}\left( -1-\exp\left(2i\pi\frac{k}{n+1}\right) \right) &=1-1+1-1\pm\cdots+1\\ &=1 \end{align} $
　$\therefore\begin{align} 　\prod_{k=1}^{n}\left( \exp\left(\frac{2i\pi k}{n+1}+1\right) \right) &=1 \end{align} $

だいぶ脱線しましたが、これで$m$ が奇数、$n$ は偶数のときの計算が完成です。

　${\displaystyle \begin{align} \det(A_{m,n}) &=\left(\prod_{j=1}^{\frac{m+1}{2}}\prod_{k=1}^{\frac{n}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ \end{align} }$

$m$ が偶数、$n$ は奇数のとき

$(m:even,n:odd)$

$A_{4,3}$ の固有値

場合分けの最後、$m$ が偶数、$n$ が奇数のときも同じように計算を進めましょう。

　${\displaystyle \begin{align} \det(A_{m,n}) &=\prod_{j=1}^{m}\prod_{k=1}^{n} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\\ &=\prod_{j=1}^{m}\prod_{k=1}^{\frac{n-1}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\\ 　　 &\qquad\times\prod_{j=1}^{m}\prod_{k=\frac{n+1}{2}}^{\frac{n+1}{2}} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)\\ &=\left(\prod_{j=1}^{\frac{m}{2}}\prod_{k=1}^{\frac{n-1}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ 　　 &\qquad\times\underbrace{\prod_{j=1}^{m}\prod_{k=\frac{n+1}{2}}^{\frac{n+1}{2}} 　　 \left(2\cos\frac{\pi j}{m+1}+i\cdot2\cos\frac{\pi k}{n+1}\right)}_{=(-1)^{\frac{m}{2}}}\\ &=(-1)^{\frac{m}{2}}\left(\prod_{j=1}^{\frac{m}{2}}\prod_{k=1}^{\frac{n+1}{2}} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2\\ \end{align} }$

　$3$ 行目から $4$ 行目の変形に注目してください。わざわざ 積が $1$ になる項を乗じています。なぜこんなことをしているかというと、あとで場合分けのない $1$ つの式に統合するときに都合がいいからです。

　また、$3$ 行目で $=(-1)^{\frac{m}{2}}$ すなわち $\pm1$ となっている部分。本当に $\pm1$ になるのかあやしいと思いませんか?念の為確認しておきましょう。

$m$ が偶数であることに注意しながら計算を進めます。

　${\displaystyle \begin{align} &\prod_{j=1}^{m}\prod_{k=\frac{n+1}{2}}^{\frac{n+1}{2}} 　　 \left(2\cos\frac{\pi j}{m+1}+\underbrace{i\cdot2\cos\frac{\pi k}{n+1}}_{=0}\right)\\ &=\prod_{j=1}^{m} 　　 2\cos\frac{\pi j}{m+1}\\ &=\prod_{j=1}^{m} \left(\exp\left( \frac{i\pi j}{m+1} \right) +\exp\left( -\frac{i\pi j}{m+1} \right) \right)\\ &=\prod_{j=1}^{m} \exp\left( -i\pi\cdot\frac{j}{m+1} \right) \left(\exp\left( \frac{2i\pi j}{m+1} \right) +1 \right)\\ &=\exp\left( -i\pi\cdot\frac{\frac{m(m+1)}{2}}{m+1} \right) \prod_{j=1}^{m} \left(\exp\left( \frac{2i\pi j}{m+1} \right) +1 \right)\\ &=(-1)^{\frac{m}{2}} \underbrace{ \prod_{j=1}^{m} \left(\exp\left( \frac{2i\pi j}{m+1} \right) +1 \right)}_{=1}\\ &=(-1)^{\frac{m}{2}}\\ \end{align} }$

手順 $5$　公式の完成

　場合分けして計算した結果をまとめるとこうなります。

　これらの式は、次のように $1$ 本の式にまとめることができます。

　$m\times n$ のドミノタイリングの総数を $Z_{m,n}$ とすると、

　$Z_{m,n}=\sqrt{\left|\det(A_{m,n})\right|}$

　でした。代入すると

　${\displaystyle \begin{align} Z_{m,n} &=\sqrt{\left(\prod_{j=1}^{\left\lceil\frac{m}{2}\right\rceil}\prod_{k=1}^{\left\lceil\frac{n}{2}\right\rceil} 　　 \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right)\right)^2} \end{align} }$

　平方根を外せば公式の完成です!!

おわりに

　というわけで、細部は省略しましたが、とにかくも公式が導出できました!
　なお、導出に使った隣接行列の配置は、参考文献をもとに私が考案した配置です。

　・・・とはいえ、本質的には参考文献で使われていた、二部グラフから作られたカステレイン行列と同じものですし、このようなシンプルな配置に誰も気が付かなかったとは考えにくいので、おそらくどこかで既出なのだろうと思います。

　また、導出の途中で証明した

　　${\displaystyle \prod_{k=1}^{n} \left(4\cos^2\frac{\pi k}{2n+1}\right)=1 }$

の部分については、X(旧Twitter)にて立見鶏 (@StandeeCock)さんに幾何的な別解を教えていただきました。

1≦a[i]≦nで
a[i]が偶数ならa[i+1]=a[i]/2
a[i]が奇数ならa[i+1]={2n+1-a[i]}/2
とするようにして幾つかの輪っかを作る。
n=5なら1-5-3-4-2-1
n=7なら1-7-4-2-1と3-6-3と5
輪っかの逆順で正2n+1角形内の二等辺三角形を順に作り、底辺部分をcosで表し続けていくと循環するはず。
添付図はn=5の場合。
添付図
pic.twitter.com/gypcNwhAE3

— 立見鶏 (@StandeeCock) September 11, 2023

　幾何的に証明できるとは驚きですね。

　それでは、【前編～導出～】の記事はここで終了となります。【後編～証明～】では、ドミノタイリングの総数と行列式の関係がなぜ成り立つのかについて掘り下げたいと思います。
　是非、【後編】の記事もご覧ください!

リンク: Mathlog|ドミノタイリングの数え上げ公式の導出方法【後編～証明～】

　(2023.11.4 追記)
　また、この方法を一般化し、任意のポリオミノをドミノで埋め尽くす方法の総数を求められる行列の構成方法を考案しましたので、こちらの記事もご覧ください!

リンク: Mathlog|任意のポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求める方法(日曜数学会)