ドミノタイリングの数え上げ公式の導出方法【後編~証明~】
はじめに
この記事は、$m \times n$ の長方形をドミノタイリングする方法が何通りあるかを計算する公式について考察する記事の後編になります。
前編の記事をお読みでない方は、まずこちらで前編の記事を読んでからこの記事を読むことをお勧めします。
リンク: Mathlog|ドミノタイリングの数え上げ公式の導出方法【前編~導出~】
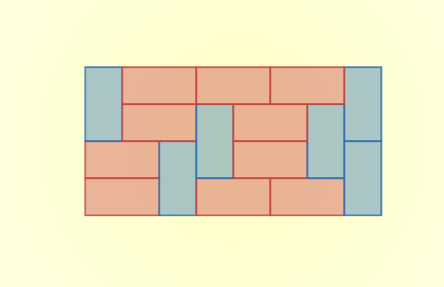 ドミノタイリングの例
ドミノタイリングの例
公式の確認
では、前編で導出した公式をまず確認しましょう。
${\displaystyle \begin{align} Z_{m,n} &=\prod_{j=1}^{\left\lceil\frac{m}{2}\right\rceil}\prod_{k=1}^{\left\lceil\frac{n}{2}\right\rceil} \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right) \end{align} }$
前編記事では次のような流れで公式を導出しました。
$m\times n$ の長方形のドミノタイリングの総数 $Z_{m,n}$ の求め方
$1$ 複素数平面の格子点に $m\times n$ 個の頂点を長方形に並べる
$2$ 隣接行列 $A_{m,n}$を作る。成分は隣接していない場合は $0$ 、隣接している場合は隣の頂点との差分により $\pm1,\pm i$ のいずれかとする。
$3$ 固有値を使って隣接行列の行列式 $\det(A_{m,n})$ を求める。
$4$ $Z_{m,n}=\sqrt{\left|\det(A_{m,n})\right|}$ に代入すると公式が得られる
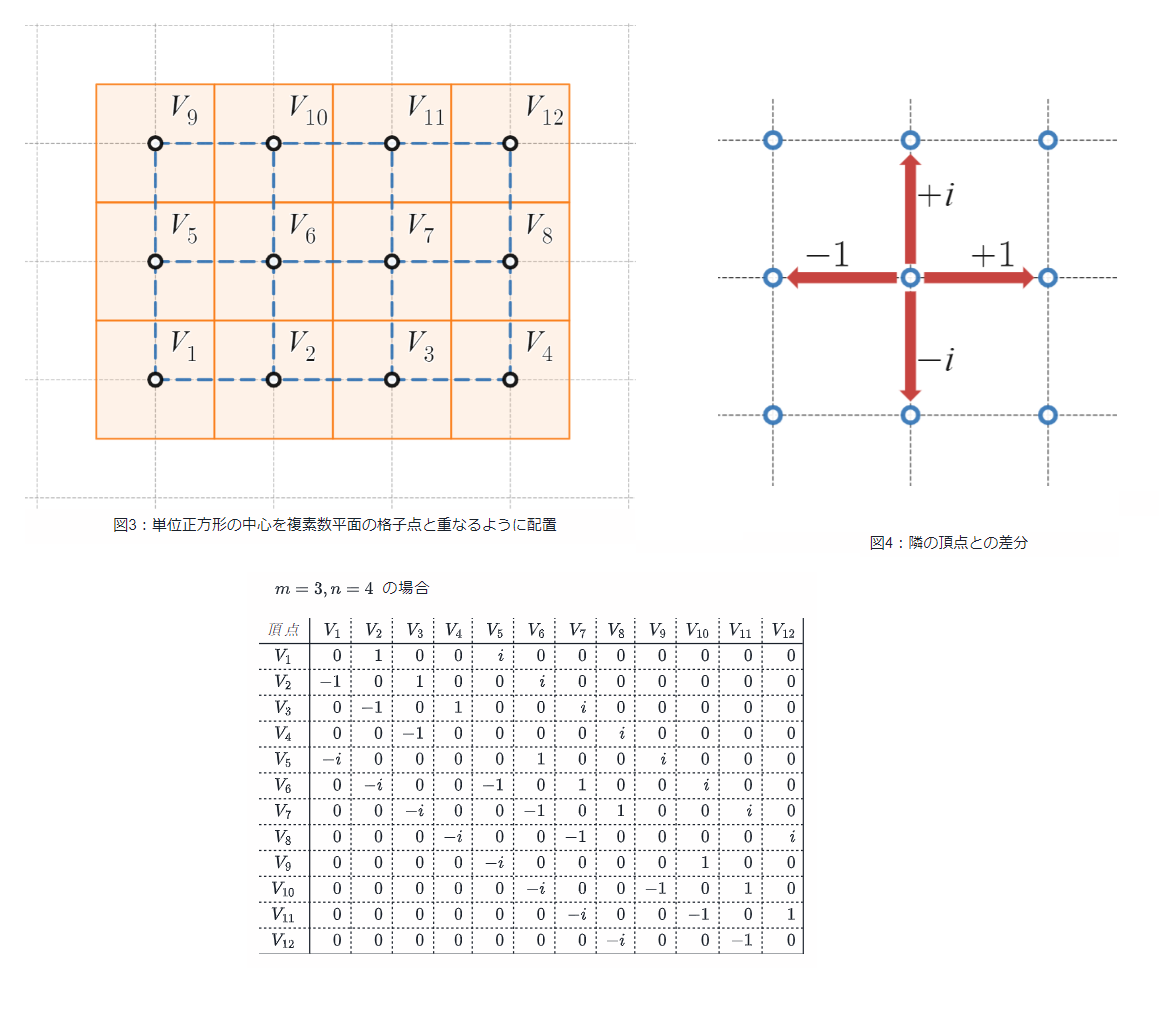 m=3,n=4 の場合の隣接行列(前編の記事より引用)
m=3,n=4 の場合の隣接行列(前編の記事より引用)
前編記事では、 $Z_{m,n}=\sqrt{\left|\det(A_{m,n})\right|}$ が成立することは $10$ 以下の $m,n$ での計算結果で観察しただけで、「なぜこの式が成り立つのか」については説明していませんでした。
説明がないことにモヤモヤしていた方、おまたせしました!
この後編記事では、まさに「なぜこの式が成り立つのか」について解説したいと思います。
パフィアンとは
ドミノタイリングの総数と行列式の関係を理解するにはパフィアンについて知っている必要があります。まず、パフィアンについて説明します。
パフィアン(Pfaffian)もしくはパフ式とは、一般的には偶数次の交代行列(=反対称行列・歪対称行列)に対して定義されるものです。
「交代行列」についてわからない方は(ここをクリック/タップ)
正方行列 $A$ が
$A^{\mathrm{T}}=-A$
をみたすとき,交代行列 (=反対称行列・歪対称行列 alternating matrix) といいます。
例えば次のような行列は交代行列です。
\begin{pmatrix} 0 & 2 & 1 \\ -2 & 0 & 3 \\ -1 & -3 & 0 \\ \end{pmatrix}
交代行列は、必ず次のような形になっています。
\begin{pmatrix} 0 & & & & \\ & 0 & & \large{A} & \\ & & 0 & & \\ & -\large{A^{\mathrm{T}}} & & 0 & \\ & & & & 0 \end{pmatrix}
パフィアンの定義
$2n\times 2n$ の交代行列 $A=(a_{ij})_{i,j=1}^{2n}$ のパフ式 $\operatorname{Pf} (A)$ は
${\displaystyle\operatorname{Pf} (A)=\sum_{\sigma\in F_{2n}}
\operatorname{sgn}(\sigma)\prod_{t=1}^{n}a_{\sigma(2t-1)\sigma(2t)}
}$
という総和で与えられる。ここで $F_{2n}$ は $1,2,\cdots,2n-1,2n$ の上の置換 $\sigma$ で
$\sigma(2i-1)<\sigma(2i)\qquad(i=1,2,\cdots,n)$
$\sigma(1)<\sigma(3)<\cdots<\sigma(2n-1)$
という条件を満たすもの全体の集合を表す。
……初見ではよくわからないと思いますので、少しくわしく説明します。
まず、「置換」についてですが、この記事では単に「$1,2,3,\cdots,2n$」と並んだ数字の列を並び替えることと思えばよいでしょう。
$\mathrm{sgn}$ は置換の符号を表しています。
$\sigma$ が奇置換のとき $\operatorname{sgn}(\sigma)=-1$
$\sigma$ が偶置換のとき $\operatorname{sgn}(\sigma)=1$
奇置換・偶置換というのは、ここでは「$2$ つの数字の入れ替え」という操作を何回合成すればその置換になるかを調べて、その回数が奇数なら奇置換、偶数なら偶置換、と考えれば良いでしょう。
たとえば、「$1,2,3,4$」を「$1,3,2,4$」に並び替えるのは奇置換、「$2,1,4,3$」に並び替えるのは偶置換となります。
<関連記事: Mathlog|15パズルのパリティと転倒数 >
それから、定義 $2$ の中のこの部分についてですが
$\sigma(2i-1)<\sigma(2i)\qquad(i=1,2,\cdots,n)$
$\sigma(1)<\sigma(3)<\cdots<\sigma(2n-1)$
この条件、一見すると複雑そうに見えますが、実は、「2つずつの数字のペアを作り、数字の小さい方が左になるように並び替えたもの」を数式で表したものにすぎません。
別の言い方をすると、「$1,2,\cdots,2n-1,2n$ を $2$ つずつ $n$ 個のペアに組む方法を全部並べ、標準的な並べ方として、各ペアの左側を右側より小さく選び、 $n$ 個のペアを、左側の数字が小さい順に並べたもの」、と考えるとわかりやすいかもしれません。
たとえば、$6$ 次対称行列のパフィアンを計算するには、
${1,2,3,4,5,6}$ を $2$ つずつ $3$ 個のペアに組む方法を並べて
$\{(1,2),(3,4),(5,6)\}$
$\{(1,2),(3,5),(4,6)\}$
$\{(1,2),(3,6),(4,5)\}$
$\{(1,3),(2,4),(5,6)\}$
$\qquad\vdots\qquad$(中略 全部見るにはここをクリック/タップ)
$\{(1,3),(2,5),(4,6)\}$
$\{(1,3),(2,6),(4,5)\}$
$\{(1,4),(2,3),(5,6)\}$
$\{(1,4),(2,5),(3,6)\}$
$\{(1,4),(2,6),(3,5)\}$
$\{(1,5),(2,3),(4,6)\}$
$\{(1,5),(2,4),(3,6)\}$
$\{(1,5),(2,6),(3,4)\}$
$\{(1,6),(2,3),(4,5)\}$
$\{(1,6),(2,4),(3,5)\}$
$\{(1,6),(2,5),(3,4)\}$
となります。これを元にパフィアンを計算する方法を表にすると
| ペア | $\mathrm{sgn}$ | 乗じる成分 |
|---|---|---|
| $\{(1,2),(3,4),(5,6)\}$ | + | $a_{1,2}a_{3,4}a_{5,6}$ |
| $\{(1,2),(3,5),(4,6)\}$ | - | $a_{1,2}a_{3,5}a_{4,6}$ |
| $\{(1,2),(3,6),(4,5)\}$ | + | $a_{1,2}a_{3,6}a_{4,5}$ |
| $\{(1,3),(2,4),(5,6)\}$ | - | $a_{1,3}a_{2,4}a_{5,6}$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
| $\{(1,6),(2,5),(3,4)\}$ | + | $a_{1,6}a_{2,5}a_{3,4}$ |
という感じになります。
では、$m\times n$ の長方形のドミノタイリングに対応する行列 $A_{m,n}$ を思い出してください。
$A_{m,n}$ は交代行列ですから、パフィアンを考えることができます。
パフィアンの計算の際に作るペアは、長方形上の頂点のペアに対応しています。
すると、隣接しないペアの部分は $a_{j,k}=0$ になり、隣接するペアの部分は $a_{j,k}\in\{1,i\}$ となりますから、パフィアンの計算上、すべてのペアが隣接する頂点に対応している場合だけ計算に寄与し、$1$ つでも隣接しない頂点のペアを含んでいる場合には計算に寄与しないことになります。
$2 \times 3$ の場合について具体的にパフィアンの計算過程を動画にしてみました。
$A_{2,3}=\begin{pmatrix} 0 & 1 & 0 & i & 0 & 0 \\ -1 & 0 & 1 & 0 & i & 0 \\ 0 & -1 & 0 & 0 & 0 & i \\ -i & 0 & 0 & 0 & 1 & 0 \\ 0 & -i & 0 & -1 & 0 & 1 \\ 0 & 0 & -i & 0 & -1 & 0 \\ \end{pmatrix}$
![!FORMULA[90][-1969434975][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FrEBwC6QlVttTW5LQ8em4.gif?alt=media) $\operatorname{Pf} (A_{2,3})$
$\operatorname{Pf} (A_{2,3})$
まず、行列の成分 $\pm1,\pm i$ のうちパフィアンの計算で使われているのは $1,i$ だけで、$-1,-i$ は使われていません。
これは、パフィアンの定義から、計算で使われるのは行列の右上部分だけだからです。
 計算で使われるのは右上の三角形の配置の部分のみ
計算で使われるのは右上の三角形の配置の部分のみ
次に注目していただきたいのは、ドミノタイリングが成立しない組合せのときは積の値がゼロになり、成立する組合せのときはゼロではないということです。これは、隣接しない頂点のペアに対応する成分がゼロなので、$1$ つでも隣接しないペアがあるとその積がゼロになってしまうからです。
そして、これが一番のポイントですが、全ての頂点のペアが隣接しているとき、すなわちドミノタイリングが成立するとき、$\operatorname{sgn}(\sigma)$ はプラスの場合もマイナスの場合もあるにもかかわらず、計算に与える影響は常に同じ値($=i$)になっています!
なお、上の例の場合($m=3,n=4$)は積が $i$ になりましたが、$m,n$ の値によっては、$\pm1,\pm i$ のいずれかの値になります。
(どの値になるかについてはのちほど説明します。)
「なぜ隣接する場合の成分を全て $1$ にせず、縦方向を $i$ にしたのか」の理由がまさにこれになります。
つまり、辺の重みを横方向 $1$ 、縦方向 $i$ としたことによって、パフィアンの計算時に発生する符号の交代をキャンセルすることができているのです!
そのことにより、ドミノタイリングの総数とパフィアンの絶対値が一致することになります。
(「どうして縦方向の辺の"重み"を $i$ にすると符号の交代をキャンセルできるのか」についてはのちほど説明します。)
ともかく、縦方向の辺の"重み"を $i$ にすることにより、ドミノタイリングが成立する場合は次のようになります。
${\displaystyle\operatorname{sgn}(\sigma)\prod_{t=1}^{mn/2}a_{\sigma(2t-1)\sigma(2t)}= \begin{cases} \mathcal{E}&\qquad \text{ドミノタイリングが成立する場合}\\ 0&\qquad \text{ドミノタイリングが成立しない場合}& \end{cases} }$
ただし、$\mathcal{E}$ は $m,n$ によって定まる値で、$\pm1,\pm i$ のいずれかの値をとる。
したがって、パフィアンはこうなります。
${\displaystyle \begin{align} \operatorname{Pf} (A_{m,n})&=\sum_{\sigma\in F_{mn}} \operatorname{sgn}(\sigma)\prod_{t=1}^{mn/2}a_{\sigma(2t-1)\sigma(2t)}\\ &=Z_{m,n}\cdot\mathcal{E}\\ \end{align} }$
両辺の絶対値をとって
$Z_{m,n}=\left|\operatorname{Pf}(A_{m,n})\right|$
つまり、ドミノタイリングの総数は、対応する行列のパフィアンの絶対値と一致するということですね。
しかし、パフィアンのままでは計算が大変なので、公式の導出の際には次に説明するパフィアンと行列式の関係を利用しています。
パフィアンと行列式の関係
交代行列の行列式とパフィアンには次の関係があることが知られています。
${\displaystyle \operatorname {det} (A)=(\operatorname {Pf} (A))^{2}}$
証明はちょっと難しいので、一旦飛ばします。
(気になる方は、この記事の最後に「おまけ」として解説していますのでそちらをごらんください。)
この関係について「パフィアンは行列式の平方根」という言い方をすることもあります。
$m,n$ がともに奇数の場合は $A_{m,n}$ は奇数次の交代行列となるため通常の意味でのパフィアンは定義されませんが、「奇数次の交代行列のパフィアンはゼロである」と解釈すれば済む話(それに、奇数次の交代行列の行列式は必ずゼロになることが知られています。)なので、この記事ではわざわざ場合分けはしません。
なお、この記事では複素行列を扱っているので、行列式やパフィアンが複素数になる場合があることに注意してください。
$A_{m,n}$ についてこの関係式の両辺の絶対値をとると
${\displaystyle \begin{align} \left|\operatorname {det} (A_{m,n})\right| &=\left|(\operatorname {Pf} (A_{m,n}))^{2}\right|\\ &=(\left|\operatorname {Pf} (A_{m,n})\right|)^{2}\\ &=Z_{m,n}^{2}\\ \end{align} }$
$\therefore Z_{m,n}=\sqrt{\left|\operatorname {det} (A_{m,n})\right|}$
これで、ドミノタイリングの総数と行列式が、パフィアンを通してつながることを確認できました。
どうして縦方向の辺の"重み"を $i$ にすると符号の交代をキャンセルできるのか
では、パフィアンを計算する際に、横軸(実軸)方向の重みを $1$ 、縦軸(虚軸)方向の重みを $i$ にすると、どうして置換の符号の交代をキャンセルすることができるのでしょうか。それをここから解説します。
パフィアンの計算の際に、置換 $\sigma$ を渡って総和を計算しますが、そのうち、ゼロにならない置換、すなわちドミノタイリングが成立する置換を $2$ つ選んで $\sigma^{[A]},\sigma^{[B]}$ とします。
また、$\sigma^{[A]},\sigma^{[B]}$ に対応する辺の重みの総積を $\mathcal{E}^{[A]},\mathcal{E}^{[B]}$ とします。
$\mathcal{E}^{[A]}=\prod_{t=1}^{mn/2}a_{\sigma^{[A]}(2t-1)\sigma^{[A]}(2t)}$
$\mathcal{E}^{[B]}=\prod_{t=1}^{mn/2}a_{\sigma^{[B]}(2t-1)\sigma^{[B]}(2t)}$
ここでの目標は、辺に重みをつけることで置換による符号の交代がキャンセルされることを示すことです。式で表すとこうなります。
$\sigma^{[A]},\sigma^{[B]}$ の選び方にかかわらず、次の等式は常に成り立つ。
${\displaystyle
\operatorname{sgn}(\sigma^{[A]})\mathcal{E}^{[A]}
=\operatorname{sgn}(\sigma^{[B]})\mathcal{E}^{[B]}
}$ ……(★)
交互閉路とは
次に、交互閉路について説明します。
任意に選んだドミノタイリングに対応する置換、 $\sigma^{[A]},\sigma^{[B]}$ にそれぞれ対応するグラフをぴったり重ね、「重なった辺は消す」という操作をすると、次の図のように辺がループ状につながった経路があらわれます。これを「交互閉路」と呼びます。
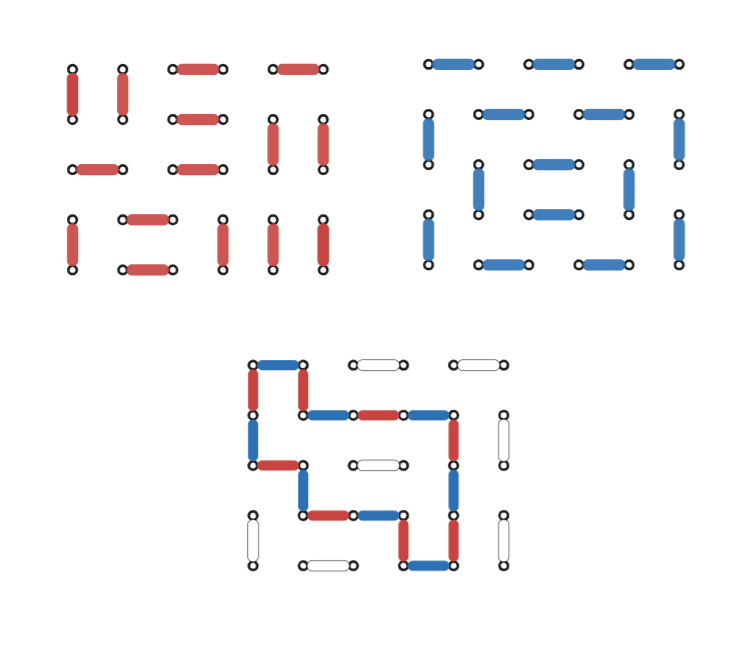 交互閉路
交互閉路
必ずループ状になる
交互閉路が必ずループ状になることは次のように説明できます。
ドミノタイリングに対応するグラフの各頂点には、必ず $1$ つの辺が伸びています。したがって、交互閉路上の頂点には、必ず $2$ つの辺が伸びていることになります。
そうすると、交互閉路上の頂点をたどっていったときに枝分かれも行き止まりも発生しないことになります。
したがって、その経路はループ状にしかなりえません。
交互閉路上の「回転」とは
例えば交互閉路上の辺を交互に赤色、青色に塗り分けると、「赤色に対応するグラフ」「青色に対応するグラフ」それぞれからドミノタイリングに対応するグラフが得られます。また、赤色と青色を切り替える操作は、あたかも交互閉路上の辺が回転移動するように見えることから、この操作を「回転」と呼びます。
交互閉路上の辺に「向き」をつける
交互閉路を構成する辺に、反時計回りに「向き」をつけてみましょう。
そうすると、「上向きの辺の数」=「下向きの辺の数」となります。
同様に、「左向きの辺の数」と「右向きの辺の数」も同じになります。
そのことは、辺をベクトルで考えたとき、交互閉路 $1$ 周分のベクトルの和がゼロになることからわかります。
そのことから、交互閉路がもつ、次のような性質がわかります。
・ 「上向きの辺の数 $+$ 右向きの辺の数」 $=$ 「全ての辺の数」 $\div2$
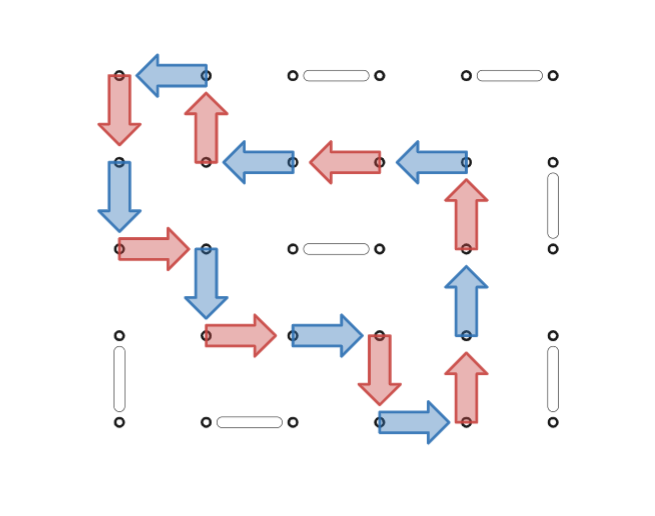 向きごとの辺の数を調べる
向きごとの辺の数を調べる
交互閉路が $1$ つだけの場合のみ考えれば良い
$\sigma^{[A]}$ に対応する配置と $\sigma^{[B]}$ に対応する配置が、交互閉路 $C$ の「回転」で互いに移りあうときに(★)が成り立つことを確認します。
このとき、交互閉路は複数ある場合もありますが、交互閉路が $1$ つだけの場合について考えるだけで十分です。
なぜなら、交互閉路が $1$ つだけの場合について(★)が成り立つならば、それを繰り返し適用することで、交互閉路が複数の場合についても(★)が成り立つことがいえるからです。
というわけで、ここからは交互閉路が $1$ つだけの場合について考えます。
辺の重みの総積のパリティ
交互閉路 $C$ 内の単位正方形の数を $S$ とします。
ここからは、交互閉路 $C$ 上で「回転」操作をしたとき、辺の重みの総積は交互閉路内の単位正方形の数のパリティ(偶奇)、すなわち $S$ のパリティ
と連動して変化することを示します。
交互閉路上の辺を図 $6$ 左側のように赤・青に交互に塗り分けます。
タテの辺のうち赤いものが $a$ 本、青いものが$b$ 本あるとします。
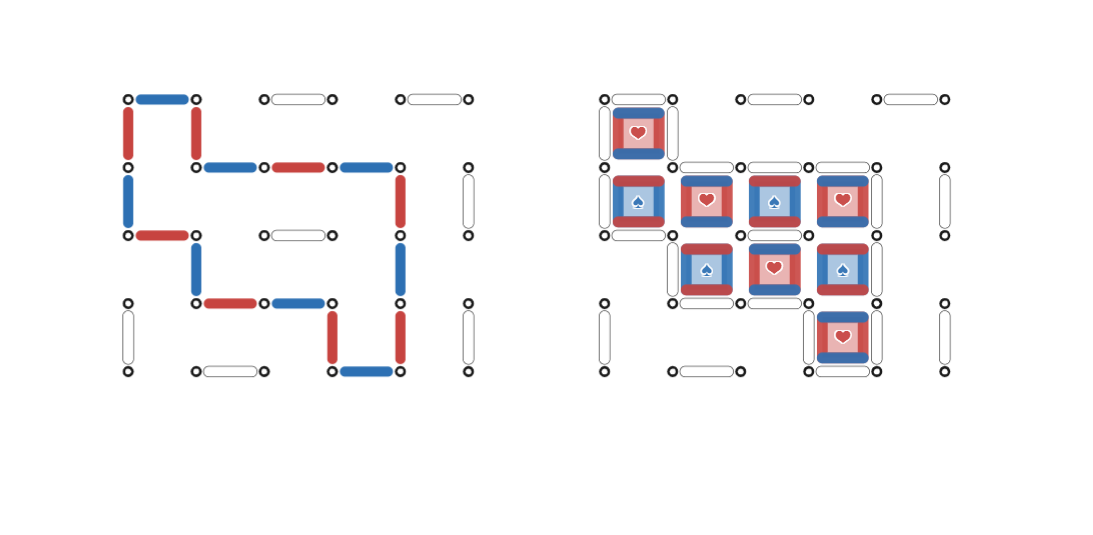 交互閉路を単位正方形に分割
交互閉路を単位正方形に分割
交互閉路内を単位正方形で、図 $6$ 右側のように「分割」します。
このうち、左右の辺が赤い正方形(❤)が $A$個、逆に左右の辺が青い正方形(♠)が $B$ 個あるとします。
チェス盤の黒マス白マスのように交互に並ぶことに注意してください。
そして、タテの辺のうち、交互閉路の内部で接している部分が $x$ 組あるとします。
このとき、次の関係があることが図からわかります。
$a=2A-x$
$b=2B-x$
$A+B=S$
$\mathcal{E}^{[A]}$ と $\mathcal{E}^{[B]}$ の計算に現れる $i$ の数の差は、$a$ と $b$ の差になることが図からわかります。
$b-a$ を計算します。
${\displaystyle \begin{align} b-a&=(2B-x)-(2A-x)\\ &=2B-2A\\ &=2(S-A)-2A\\ &=2S-4A\\ \end{align} }$
$i^4=1$ を考慮して、以下 $\mod4$ で考えます。
$S$ が偶数のときは
$b-a\equiv0\,\mod4$
となり、$\mathcal{E}^{[A]}=\mathcal{E}^{[B]}$ となります。
$S$ が奇数のときは
$b-a\equiv2\,\mod4$
となり、$\mathcal{E}^{[A]}=i^2\mathcal{E}^{[B]}$ すなわち $\mathcal{E}^{[A]}=-\mathcal{E}^{[B]}$ となります。
つまり、交互閉路が切り替わった時に辺の重みの総積は $(-1)^{S}$ 倍になるということです。
$\mathcal{E}^{[A]} \cdot (-1)^{S}=\mathcal{E}^{[B]}$
交互閉路上の頂点数のパリティ
交互閉路 $C$ 上の頂点数を $2V_e$とします。
頂点数は必ず偶数になるため、$V_e$ は整数です。
ここからは、交互閉路 $C$ 上で「回転」操作をしたとき、置換のパリティすなわち ${\operatorname{sgn}(\sigma)}$ が、交互閉路 $C$ 上の辺の数の偶奇、すなわち $V_e$ のパリティと連動して変化することを示します。
まず、$\sigma^{[A]}$ のうち、交互閉路上の辺に対応する頂点が、反時計回りの順番になるように並び替えたものを$\sigma^{[A]\prime}$ とします。
$\sigma^{[B]}$ についても同様に並び替えたものを 、$\sigma^{[B]\prime}$ とします。
このとき、「ある頂点のペア」と「別の頂点のペア」を交換する操作は偶置換なので入れ替えても $\operatorname{sgn}(\sigma)$ の符号は変わりませんが、「ある頂点のペア」の中で頂点の順番を入れ替えると奇置換なので符号が交代することに注意してください。
交互閉路を構成する頂点を $1$ つ選び、そこから順番に番号を振って、
$P_1,P_2,\cdots ,P_{2V_e}$
とします。
このとき、次のような置換を考えます。
$\pmatrix{ P_1&P_2&P_3&\cdots&P_{2V_e}\\ P_{2V_e}&P_1&P_2&\cdots&P_{2V_e-1} }$
上の行、下の行がそれぞれ頂点の組を表しているものと考えます。イメージとしては、$\sigma^{[A]}$ に対応する辺に赤色を、$\sigma^{[B]}$ に対応する辺に青色を付けたとして
赤い辺の組 $(P_1,P_2),(P_3,P_4),\cdots,(P_{2V_e-1},P_{2V_e})$
青い辺の組 $(P_{2V_e},P_1),(P_2,P_3),\cdots,(2P_{V_e-2},2P_{V_e-1})$
になる、という感じです。
頂点の組に対応する辺が、上の行と下の行で「回転」しているのがわかりますでしょうか。
このとき、この置換は必ず奇置換となります。
なぜなら、要素数が偶数の巡回置換は奇置換になるからです。
次に、交互閉路上の辺に反時計回りに「向き」をつけたとき「左向き、又は下向きの辺」のうち、赤色の辺の数が $N_r$ 個、青色の辺の数が $N_b$ 個とします。
言い換えると、複素数平面で実軸負の向き又は虚軸負の向きのもののうち、赤色の辺の数と青色の辺の数、ということです。
$N_r+N_b=V_e$
となります。
$\sigma^{[A]}$ と $\sigma^{[A]\prime}$ は $N_r$ 回の互換で遷移し、 $\sigma^{[B]}$ と $\sigma^{[B]\prime}$ は $N_b$ 回の互換で遷移します。また、 $\sigma^{[A]\prime}$ と $\sigma^{[B]\prime}$ は奇置換で遷移しますので
$\mathrm{sgn}(\sigma^{[A]\prime})=(-1)^{N_r}\cdot\mathrm{sgn}(\sigma^{[A]})$
$\mathrm{sgn}(\sigma^{[B]\prime})=(-1)^{N_b}\cdot\mathrm{sgn}(\sigma^{[B]})$
$\mathrm{sgn}(\sigma^{[A]\prime})=-\mathrm{sgn}(\sigma^{[B]\prime})$
第 $1$ 式の両辺を入り替えたものと、第 $2$ 式の辺々を掛け合わせ、第 $3$ 式を使って整理すると次の式が得られます。
$\mathrm{sgn}(\sigma^{[A]})=(-1)^{N_r+N_b-1}\cdot\mathrm{sgn}(\sigma^{[B]})$
$V_e=N_r+N_b$ ですから、次の関係式が得られます。
$\operatorname{sgn}(\sigma^{[A]})=(-1)^{V_e-1}\cdot{\operatorname{sgn}(\sigma^{[B]})}$
……このあたりの感覚は数式で表すと難しく見えてしまうかもしれませんが、実際にはパリティがどうなるかを観察しているだけのことですので、数式から理解しようとするより、頂点の置換回数が偶数か奇数か、感覚的にとらえてもらったほうがわかりやすいかもしれません。
補題 $3$ と補題 $4$ を再掲します。
(補題 $3$) $\mathcal{E}^{[A]} \cdot (-1)^{S}=\mathcal{E}^{[B]}$
(補題 $4$) $\operatorname{sgn}(\sigma^{[A]})=(-1)^{V_e-1}\cdot{\operatorname{sgn}(\sigma^{[B]})}$
補題 $3$ と補題 $4$ の辺々かけて次の関係を得ます。
${\operatorname{sgn}(\sigma^{[A]})}\cdot\mathcal{E}^{[A]} \cdot(-1)^{S-V_e+1}={\operatorname{sgn}(\sigma^{[B]})}\cdot\mathcal{E}^{[B]} $
交互閉路 $C$ 上の頂点数と $C$ 内の単位正方形数のパリティ
いよいよ大詰めです。最後に ${(-1)^{S-V_e+1}=1 }$ を示します。
突然ですが、交互閉路に対して「ピックの定理」を使います。
ピックの定理は等間隔に点が存在する平面上にある多角形の面積を求める公式である。この場合の多角形の頂点は全て、最も近い点同士の間隔を$1$とする正方格子点上にあり、内部に穴は開いていないものとする。多角形の内部にある格子点の個数を $V_i$、辺上にある格子点の個数を $b$ とするとこの種の多角形の面積 $S$ は以下の式で求められる。
${\displaystyle S=V_i+{\frac {1}{2}}b-1}$
例えば図の六角形なら内部にある点が $V_i = 39$ 個、辺上にある点が $b = 14$ 個なので$ S = 39 + 14/2 − 1 = 45$ と簡単に計算できる。
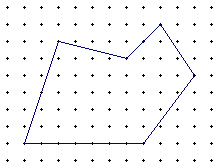 画像の名前
画像の名前
(画像・文章はWikipedia(ja)「ピックの定理」) より引用)
交互閉路 $C$ 内の頂点数を $V_i$とすると、ピックの定理により、次の関係が得られます。
${\displaystyle S=V_i+{\frac {1}{2}}\cdot(2V_e)-1}$
${\displaystyle \therefore V_i=S-V_e+1}$
実は、交互閉路が「ドミノタイリングが成立する置換を互いに移り合わせる」ものであるならば、$V_i$ は必ず偶数になります。なぜなら、交互閉路の内側にある頂点も必ずペアにならなければならないからです。
したがって
${\displaystyle \begin{align} (-1)^{S-V_e+1} &=(-1)^{V_i}\\ &=1 \end{align} }$
これを補題 $5$ に代入して
${\operatorname{sgn}(\sigma^{[A]})}\mathcal{E}^{[A]}={\operatorname{sgn}(\sigma^{[B]})}\mathcal{E}^{[B]}$
これこそが示すべきこと(★)でした!
少し長くなりましたので、証明の流れを簡単にまとめておきます。
$[1]$ 辺の重みの総積のパリティと交互閉路内の単位正方形の数のパリティは連動する。
$\mathcal{E}^{[A]} \cdot (-1)^{S}=\mathcal{E}^{[B]}$
$[2]$ 置換のパリティと交互閉路上の頂点数のパリティは連動する。
$\operatorname{sgn}(\sigma^{[A]})=(-1)^{V_e-1}\cdot{\operatorname{sgn}(\sigma^{[B]})}$
$[3]$ 交互閉路内の単位正方形の数のパリティと交互閉路上の頂点数のパリティは連動する。
$(-1)^{S-V_e+1}=1$
$[4]$ 置換のパリティと辺の重みの総積のパリティは連動する。すなわち置換による符号の交代がキャンセルされる。
${\operatorname{sgn}(\sigma^{[A]})}\mathcal{E}^{[A]}={\operatorname{sgn}(\sigma^{[B]})}\mathcal{E}^{[B]}$
どの値になるか
ここまでで、$\sigma$ がドミノタイリングを成立させるような置換である場合には
${\operatorname{sgn}(\sigma)}{\prod_{t=1}^{mn/2}a_{\sigma(2t-1)\sigma(2t)}}$
は $\sigma$ によらず一定の値($=\mathcal{E}$)となることを見てきました。
次に、その「一定の値」が何になるのか $m,n$ を使って表すことを考えます。
それには、次のようにタイリングが成立する場合の辺の重みの積を $1$ つ見つければよいです。
重み $1$ の辺(=横向きの辺)をできるだけたくさん敷き詰めてから、残ったスキマに重み $i$ の辺(縦向きの辺)を置いていく。
・ $n$ が偶数のときは重み $1$ の辺で全て敷き詰めることができる。このとき $\mathrm{sgn}(\sigma)=1$ であるから $\mathcal{E}=1$
・ $n$ が奇数、$m$ が偶数のときは縦1列分のスキマができるので、重み $i$ の辺を $\frac{m}{2}$ 個置くことになる。このとき $\mathrm{sgn}(\sigma)=1$ であるから $\mathcal{E}=i^{{m}/{2}}$
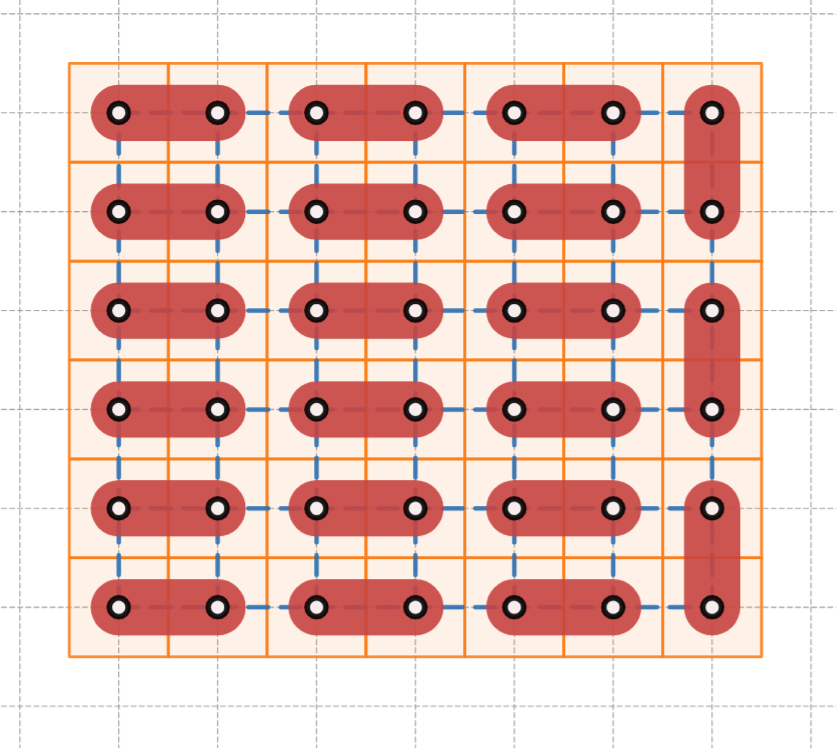 計算しやすいように敷き詰める
計算しやすいように敷き詰める
従って次のようになります。
$\sigma$ がドミノタイリングを成立させる置換である場合、
$\mathcal{E}\\ =\begin{cases} 1 &\text{(if n:even)}\\ i^{m/2} &\text{(if m:even,n:odd)} \end{cases}$
まとめ
ここまでの結果をもとに、パフィアン及び行列式を改めて $m,n$ を使って表すとこうなります。
${\displaystyle \begin{align} \mathrm{Pf} (A_{m,n}) &=Z_{m,n}\cdot\begin{cases} 1 &\text{(if n:even)}\\ i^{m/2} &\text{(if m:even,n:odd)} \end{cases} \end{align} }$
${\displaystyle \begin{align} \operatorname {det} (A_{m,n}) &=Z_{m,n}^2\cdot\begin{cases} 1 &\text{(if n:even)}\\ (-1)^{m/2} &\text{(if m:even,n:odd)} \end{cases} \end{align} }$
$m,n$ がともに奇数のときは $\operatorname {det} (A_{m,n})=Z_{m,n}=0$ であることを利用すれば、$\operatorname {det} (A_{m,n})$ を場合分けのないシンプルな式にまとめることができます。
${\displaystyle \begin{align} \operatorname {det} (A_{m,n}) &=(-1)^{n\cdot\left\lceil\frac{m}{2}\right\rceil}\cdot Z_{m,n}^2 \end{align} }$
前編記事の、$10$ 以下の $m,n$ について行列式を計算した表と一致しましたね!
おわりに
これで後編の記事は(「おまけ」を残して)終了です。
記事の完成までかなり時間がかかってしまいましたが、その分内容は充実できたのかな、と思います。
特に、計算に使った隣接行列は自分で考えたものなので、後編の証明に使ったいろいろなアイデアも自分で考えだす必要があり、他にはない独自性が出せたのではないかと思います。
実に手ごわい式でしたが、できあがった式は組み合わせ爆発をものともせずに一瞬でドミノタイリングの総数ができ、なおかつ見た目も美しい素晴らしい式だと思います。
自分の手でそれが成り立つことを確認できたことはとても楽しい体験でした。
最後に公式を再掲して、愛でながら終了にしたいと思います。
ありがとうございました!
$m\times n$ のドミノタイリングの総数(再掲)
${\displaystyle \begin{align} Z_{m,n} &=\prod_{j=1}^{\left\lceil\frac{m}{2}\right\rceil}\prod_{k=1}^{\left\lceil\frac{n}{2}\right\rceil} \left(4\cos^2\frac{\pi j}{m+1}+4\cos^2\frac{\pi k}{n+1}\right) \end{align} }$
(2023.11.4 応用編となる記事を公開しました!)
リンク:
Mathlog|任意のポリオミノをドミノで埋め尽くす方法の総数を行列式を使って求める方法(日曜数学会)
おまけ 交代行列の行列式がパフィアンの $2$ 乗となる証明
ここからは「おまけ」として、交代行列の行列式がパフィアンの $2$ 乗となる証明の解説をしたいと思います。
ただし、これは英語版のWikipediaを中心に私がネット上で拾ったものを再構成したものであり、私自身よくわかっていない部分を含んでいることをお断りしておきます。
$\operatorname{pf}(B^{\top}AB)=\det(B)\operatorname{pf}(A)$
証明にあたり、先にいくつかの補題を示します。
$n\times n$ の交代行列 $A=(a_{ij})_{i,j=1}^{n}$ について考えます。
ただし、$n$ は偶数とし、$n=2m$ とします。
任意の $n \times n$ 行列 $B=(b_{ij})_{i,j=1}^{n}$ に対し、$\operatorname{pf}(B^{\top}AB)=\det(B)\operatorname{pf}(A)$ が成り立つことを補題としてまず示します。
また、$\alpha,\beta$ を $n$ 次対称群を渡る和を計算するときの置換を表す記号として使います。
パフィアンの計算を、置換の重複を許して計算し、最後に重複度で割る方法で求めると、次の式が得られます。
${\displaystyle\operatorname{pf}(A)=\frac{1}{2^m \cdot m!}\sum_{\alpha}\left( \operatorname{sgn}(\alpha)a_{\alpha(1)\alpha(2)}\cdot\cdots\cdot a_{\alpha(n-1)\alpha(n)} \right)}$
$B$ の行列式を定義どおりに計算して次の式が得られます。
${\displaystyle\operatorname{det}(B)=\sum_{\alpha}\left( \operatorname{sgn}(\alpha)a_{1\alpha(1)}\cdot\cdots\cdot a_{n\alpha(n)} \right)}$
$\beta$ で行ごと置換すると、行列式は $\operatorname{sgn}(\beta)$ 倍になります。
${\displaystyle\operatorname{sgn}(\beta)\operatorname{det}(B)=\sum_{\alpha}\left(
\operatorname{sgn}(\alpha)a_{\beta(1)\alpha(1)}\cdot\cdots\cdot a_{\beta(n)\alpha(n)}
\right)}$
ここで、$\left(B^{\top}AB\right)_{ij}=\sum_{k=1}^{n} \sum_{l=1}^{n} b_{ki}a_{kl}b_{lj}$ であり、添え字 $k,l$ は自由に動かせるから、
${\displaystyle\begin{align} 2^{m}\cdot m!\operatorname{pf}(B^{\top}AB) &=\sum_{\alpha}\left( \operatorname{sgn}(\alpha)\left(B^{\top }AB\right)_{\alpha(1)\alpha(2)}\cdot\cdots\cdot \left(B^{\top}AB\right)_{\alpha(n-1)\alpha(n)}\right)\\ &=\sum_{\alpha}\left( \operatorname{sgn}(\alpha)\sum_{\beta}\left(b_{\beta(1)\alpha(1)}a_{\beta(1)\beta(2)}b_{\beta(2)\alpha(2)}\right)\cdot\cdots\cdot \left(b_{\beta(n-1)\alpha(n-1)}a_{\beta(n-1)\beta(n)}b_{\beta(n)\alpha(n)}\right)\right)\\ &=\sum_{\beta}\sum_{\alpha}\left( \operatorname{sgn}(\alpha)b_{\beta(1)\alpha(1)}b_{\beta(2)\alpha(2)}\cdots b_{\beta(n)\alpha(n)}\right)\cdot\cdots\cdot \left(a_{\beta(1)\beta(2)}\cdots a_{\beta(n-1)\beta(n)}\right)\\ &=\sum_{\beta}\operatorname{sgn}(\beta)\operatorname{det}(B)\left(a_{\beta(1)\beta(2)}\cdots a_{\beta(n-1)\beta(n)}\right)\\ &=\det(B)\cdot 2^m\cdot m!\operatorname{pf}(A) \end{align} }$
これで補題が示されました。
$\operatorname{pf}(B^{\top}AB)=\det(B)\operatorname{pf}(A)$
${\displaystyle A=Q^{\top}S Q}$
スペクトル理論によると、実交代行列は
${\displaystyle A=Q^{\top } S Q}$
の形に対角化できることが知られています。
ただし、$Q$ は直交行列で、$S$ は以下の形式のブロック対角行列です。
$\lambda _{k}$ は固有値の虚部を表す正実数です。
なお、$2m$ 次の実交代行列の固有値は $\pm i\lambda_1 ,\pm i\lambda_2 ,\cdots\pm i\lambda_m$ の形で表すことができることが知られています。
${\displaystyle \mathrm{S} ={\begin{bmatrix}{\begin{matrix}0&\lambda _{1}\\-\lambda _{1}&0\end{matrix}}&0&\cdots &0\\0&{\begin{matrix}0&\lambda _{2}\\-\lambda _{2}&0\end{matrix}}&&0\\\vdots &&\ddots &\vdots \\0&0&\cdots &{\begin{matrix}0&\lambda _{r}\\-\lambda _{r}&0\end{matrix}}\\&&&&{\begin{matrix}0&&\\&\ddots &\\&&0\end{matrix}}\end{bmatrix}}}$
${\displaystyle \operatorname {pf} (A)^{2}=\det(A)}$
${\displaystyle \operatorname {pf} (A)^{2}=\det(A)}$ を多項式の等式とみることで、実交代行列についてこれを証明すれば、自動的に複素交代行列の証明もできたことになります。
以下では、実交代行列を対象として計算しています。
補題 $10$ より
${\displaystyle A=Q^{\top } S Q}$
と対角化して、パフィアンの $2$ 乗を計算します。
$2$ 行目の変形に補題 $9$ を使っています。
${\displaystyle
\begin{align}
\operatorname {pf} (A)^{2}
&=\operatorname {pf} (Q^{\top} S Q)^{2}\\
&=\det(Q)^2\operatorname{pf}(S)^2\\
&=\operatorname{pf}(S)^2\\
&=\left(\prod \lambda_i\right)^2\\
&=\det(A)
\end{align}}$
${\displaystyle \operatorname {pf} (A)^{2}=\det(A)}$
以上でおまけは終了です。
……が、おまけの部分は難しすぎて私自身よくわかっていません。
この分野に詳しい方に補足の記事を書いていただけたら、嬉しいです!
