ラマヌジャンは本当に何も知らなかったのか

はじめに
ラマヌジャンとは
ラマヌジャンの論文
ラマヌジャンの円周率公式
ラマヌジャンのノートブック
ラマヌジャンの円周率公式、再び
円周率公式についての記述
モジュラー方程式についての記述
アイゼンシュタイン級数についての記述
超幾何関数についての記述
まとめ
おわりに
おまけ：関連書籍の紹介
参考文献

子葉

数学史・伝記解説

文献あり

ラマヌジャンは本当に何も知らなかったのか

円周率,ラマヌジャン

61313

はじめに

　数学好きの人間なら誰もが一度は耳にする偉人、ラマヌジャン。彼は人間離れした洞察力により数えきれないほどの発見を世に残しました。現代では彼についての数々の逸話が語り継がれていますが、その実際と比べてみると少し神格化されすぎているような気がします。もちろん彼が神懸かりとも言える発想力を持っていたことは確かだと思いますが、さも「無から有を生み出した」かのような噂が独り歩きして無闇に敬遠されてしまうのは少し残念に思います。
　この記事ではそんなラマヌジャンについて、ラマヌジャンの円周率公式
$\frac{1}{π} = \frac{2 \sqrt{2}}{99^{2}} \sum_{n = 0}^{\infty} \frac{(4 n)!}{(n!)^{4}} \frac{26390 n + 1103}{396^{4 n}}$
を例に挙げて、実際のところ彼が何を知り、何を考えた上でこのような公式を発見をしたのか、個人的に考察していきたいと思います。

ラマヌジャンとは

　数学における偉業とは問題を解決することだけではなく、問題を見出すことにもある。その点で稀代の数学者ラマヌジャンは無数の偉業を成し遂げた、まさに天から才を授けれらた人物であると言えましょう。
このガビガビの画像は誰が作ったものなのだろう

　ラマヌジャンはその32年という短い生涯の中で何千もの公式をノートに書き留めており、例えばこちらの記事で紹介されているような初等的な等式から上に挙げた円周率公式のような高度な等式まで、そのどれもが謎と魅力に満ちたものとなっていました。
　しかしこの途方もない数の公式を彼がどのように導出したのか、それは誰にも、彼自身にも説明することはできませんでした。彼が言うには「夢の中で女神様が教えてくれた」とのことです。そういった彼の性質上、彼は彼の発見した事実の多くに証明を付けることをしませんでした。聞くだにラマヌジャンは「証明」という概念を身に付けていなかったとさえ言われています。
　このようにラマヌジャンの業績は(客観的にみると)論理的裏付けに乏しいものであったのに対し、その結果はどれも正しいものばかりでした。またこのようにラマヌジャンが息を吐くように生み出した公式であっても厳密に証明するには非常に難解な議論が必要であることもありました。例えば上の円周率公式も発見(1910)から証明(1987)されるまで実に77年もの時間が必要でした。
　というのがラマヌジャンについて"一般的によく語られている"人物像となります。

ラマヌジャンの論文

　そんなラマヌジャンの不可解な経歴から「公式だけ暗記してタイムスリップしてきた未来人」などと冗談を言われれることもありますが、果たして彼は本当に何も知らなかったのでしょうか。
　これについてはラマヌジャンの書いた論文を読んでみるとわかることがあります。実はラマヌジャンも人並みに論文は執筆しており、生涯で40編の論文を発表しています。そのうちの37編はこちらのサイトやこちらのアーカイブで閲覧することができます(前者についてはpdf形式でダウンロードすることもできます)。例えばせきゅーん氏のこのツイート

"A proof of Bertrand's postulate"
"Some properties of p(n), the number of partitions of n"
などのラマヌジャンの論文を読むとラマヌジャンは普通に証明を残していると思うのですが、「ラマヌジャンが証明を残さなかった」や「知らなかった」というのは正しい歴史認識なのでしょうか。
— せきゅーん (@integers_blog) June 19, 2023

にもあるように、簡単に読める範囲では先のサイトで言う24,25番目の論文を読んでみるとラマヌジャンの証明能力が窺い知れると思います(それぞれベルトランの仮説と分割数についての論文となります)。
　実際私もラマヌジャンの円周率公式やリーマン予想に関するラマヌジャンの定理について調べていた時に同じく6,15番目の論文に目を通したことがありましたが、"We can easily show that"という文言のクソでか行間に頭を抱えたことこそあれど、ある程度再現性のある説明は為されていたように思います。

ラマヌジャンの円周率公式

　では実際にラマヌジャンの円周率公式
$\begin{aligned} \frac{1}{π} & = \frac{1}{3528} \sum_{n = 0}^{\infty} (- 1)^{n} \frac{(4 n)!}{(n!)^{4}} \frac{21460 n + 1123}{14112^{2 n}} \\ = \frac{2 \sqrt{2}}{99^{2}} \sum_{n = 0}^{\infty} \frac{(4 n)!}{(n!)^{4}} \frac{26390 n + 1103}{396^{4 n}} \end{aligned}$
を例に挙げてラマヌジャンが論文「Modular equations and approximations to π (モジュラー方程式と $π$ の近似)」にてどのような説明を行っていたのか見てみましょう(この公式はこの論文の式(39),(44)として出てきます)。
　上の論文の中ではラマヌジャンの円周率公式に直接かかわる命題として次のような事実が陰に陽に述べられています(論文の内容とは少し表現を変えています)。

楕円積分 $K (k)$ は
${(\frac{2 K}{π})}^{2} = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} (2 k k^{'})^{2 n}$
という級数展開を持つ(ただし $(x)_{n}$ はポッホハマー記号とした)。また $τ = i K^{'} / K$ ( $K^{'}$ は微分の意ではない)においてアイゼンシュタイン級数 $E_{2} (τ)$ は
$\begin{aligned} E_{2} (τ) & = \frac{4}{π^{2}} (3 k k^{' 2} K \dot{K} + (1 - 2 k^{2}) K^{2}) \\ = (1 - 2 k^{2}) \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} (3 n + 1) (2 k k^{'})^{2 n} \end{aligned}$
という級数展開を持つ。
$N$ 次モジュラー方程式
$\frac{K^{'}}{K} = N \frac{L^{'}}{L} (L = K (l))$
を満たすような $k, l$ は互いに代数的な関係にある。またこのときある代数関数 $R_{N} (k, l)$ が存在して
$N E_{2} (N τ) - E_{2} (τ) = \frac{4 K L}{π^{2}} R_{N} (k, l)$
が成り立つ。
特に自然数 $N$ に対して $K^{'} / K = \sqrt{N}$ を満たすような $k$ は代数的数となり、またある代数的数 $R_{N}$ が存在して
$E_{2} (\sqrt{- N}) = \frac{R_{N}}{2 \sqrt{N}} {(\frac{2 K}{π})}^{2} + \frac{3}{π \sqrt{N}}$
が成り立つ。これによって
$\begin{aligned} \frac{1}{π} & = \frac{\sqrt{N}}{3} E_{2} (\sqrt{- N}) - \frac{R_{N}}{6} {(\frac{2 K}{π})}^{2} \\ = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} (A n + B) (2 k k^{'})^{2 n} \end{aligned}$
という円周率公式が得られる。
一般に $s = 2, 4, 3, 6$ において
$K_{s} = \frac{π}{2} \sum_{n = 0}^{\infty} \frac{(\frac{1}{s})_{n} (1 - \frac{1}{s})_{n}}{(1)_{n}^{2}} k^{2 n}, τ_{s} = \frac{1}{\sin \frac{π}{s}} \frac{i K_{s}^{'}}{K_{s}} (q_{s} = e^{π i τ_{s}})$
とおいたとき、これらに対応する同様の理論が存在し
$\begin{aligned} \frac{1}{π} & = \frac{4}{π^{2}} (\frac{k k^{' 2}}{1 - 2 k^{2}} A K_{s} {\dot{K}}_{s} + B K_{s}^{2}) \\ = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{s})_{n} (1 - \frac{1}{s})_{n}}{(1)_{n}} (A n + B) (2 k k^{'})^{2 n} \end{aligned}$
という円周率公式が得られる(このことは"There are corresponding theories"とだけしか説明されていない)。

　見ての通りラマヌジャンは
$\frac{1}{π} = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{s})_{n} (1 - \frac{1}{s})_{n}}{(1)_{n}} \frac{A n + B}{C^{n}}$
という形の円周率公式の導出方法をほぼ完全に解明しています。実際のところ同論文で提示されている $s = 2$ の円周率公式
$\begin{aligned} \frac{4}{π} & = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} \frac{6 n + 1}{4^{n}} \\ \frac{16}{π} & = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} \frac{42 n + 5}{64^{n}} \\ \frac{32}{π} & = \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} \frac{(42 \sqrt{5} + 30) n + 5 \sqrt{5} - 1}{64^{n}} {(\frac{\sqrt{5} - 1}{2})}^{8 n} \end{aligned}$
はラマヌジャンの説明から再現することができますし、さらに言えば上に挙げた円周率公式
$\begin{aligned} \frac{1}{π} & = \frac{1}{3528} \sum_{n = 0}^{\infty} (- 1)^{n} \frac{(4 n)!}{(n!)^{4}} \frac{21460 n + 1123}{14112^{2 n}} \\ = \frac{2 \sqrt{2}}{99^{2}} \sum_{n = 0}^{\infty} \frac{(4 n)!}{(n!)^{4}} \frac{26390 n + 1103}{396^{4 n}} \end{aligned}$
に関わる重要な定数
$\begin{aligned} G_{37}^{4} & = \sqrt{37} + 6 & g_{58}^{2} & = \frac{\sqrt{29} + 5}{2} \\ (G_{37}^{12} & = \frac{21460}{4 \sqrt{37}} + \frac{14112}{16} & g_{58}^{12} & = \frac{2 \sqrt{2} \cdot 26390}{\sqrt{58}} + \frac{396^{2}}{16}) \end{aligned}$
も同論文の中で登場しています。
　もっと言うと超幾何関数の変換公式を用いれば $s = 3, 4, 6$ に対して
$\sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{2}}{(1)_{n}^{2}} k^{2 n} = m_{s} \sum_{n = 0}^{\infty} \frac{(\frac{1}{s})_{n} (1 - \frac{1}{s})_{n}}{(1)_{n}^{2}} k_{s}^{2 n}$
なる $k$ についての代数関数 $m_{s}, k_{s}$ が存在することがわかるので、 $s = 2$ の円周率公式はそのまま $s = 3, 4, 6$ の円周率公式に変形することができます。このことはラマヌジャンの論文では触れられてはいませんでしたが、少なくともGoursat (1881)には証明されている事実であり、ともすればラマヌジャンによって円周率公式の理論部分は全て解明されていたことになります。

Pi and the AGMについて

　ラマヌジャンの円周率公式はBorwein(1987)によって解決したことになっていますが、ラマヌジャンによってここまで解明されていたとなると一体何を証明するのに時間がかかったのでしょうか。私はこのあたりの歴史について詳しいことは知らないので憶測でしかありませんが、上で述べたようにラマヌジャンは円周率公式の理論部分についてはほとんど説明していたものの、その理論を用いた各定数の具体値の計算過程については記していなかったため、それらの値を厳密に計算するのに、また計算できるだけの道具が揃うのに長い時間が必要であったのだと思います(あるいは単に説明が不十分であり、行間にある理論の発展に時間がかかったのかもしれません)。
　実際Borwein兄弟が1987年に出版したのは論文ではなく"Pi and the AGM"という400ページにも及ぶ書籍でした。タイトルにもある通り、この書籍はラマヌジャンの円周率公式を主題としていたわけではなく、算術幾何平均や円周率に関係する理論を広く展開した専門書となっています。特に色々な定数や級数などの具体値や近似値を求める手法が多々紹介されており、円周率公式に関わる各定数も様々なアプローチによって計算されています。

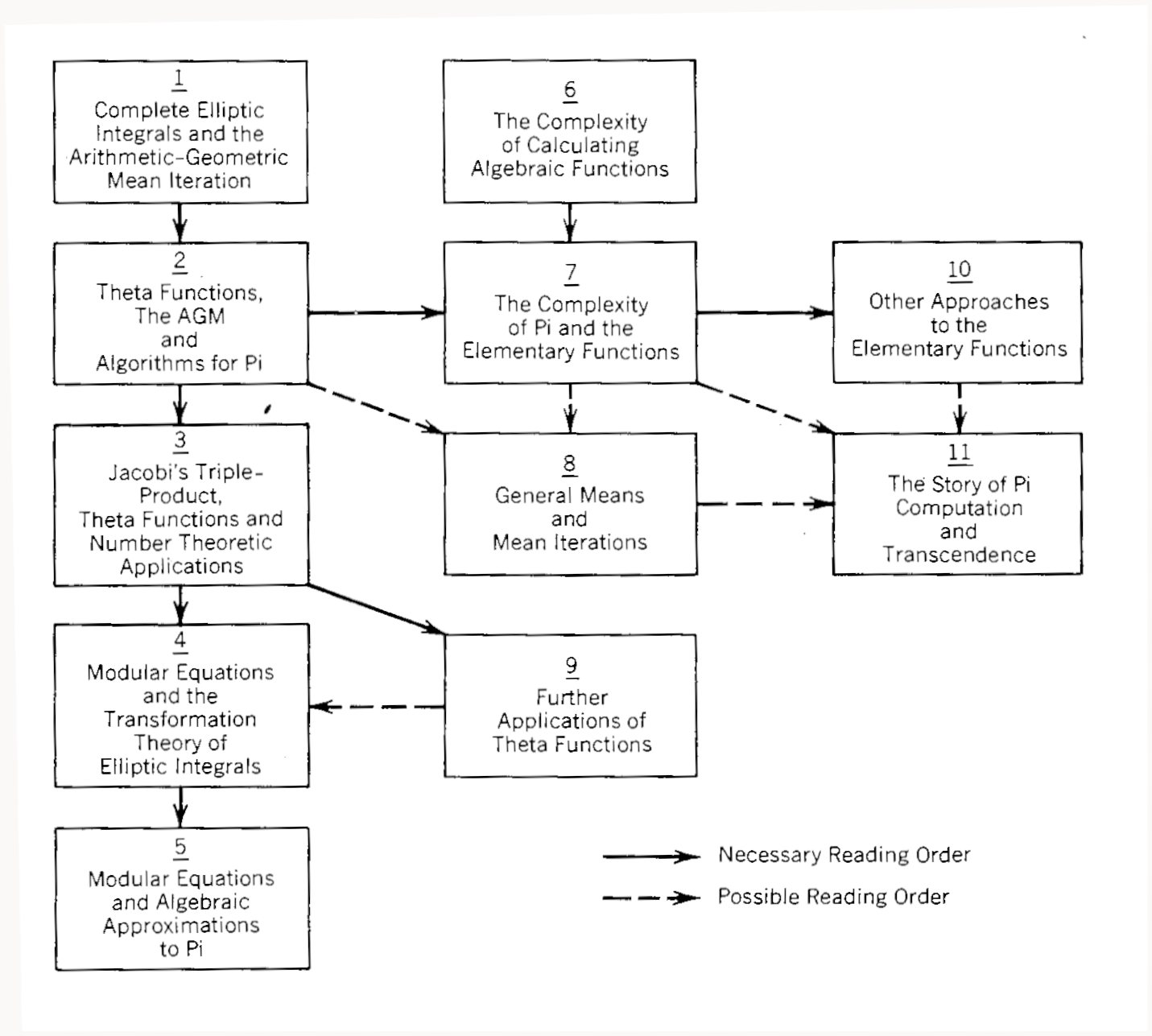Pi and the AGMの内容のフローチャート
ラマヌジャンの円周率公式は第5章にて解決されている

ラマヌジャンのノートブック

　何はともあれ「ラマヌジャンは証明能力に欠けていた」という言説は少なくとも部分的に誤りであることがわかりました。しかしこれだけの証拠では「ラマヌジャンは後付け的に説明する能力はあったというだけで、種々の公式を思い付いた段階ではやはり何の根拠もなかったのではないか」という疑問が残ります。
　この疑問についてはラマヌジャンのノートブックを読んでみるとわかることがあります。紙が非常に高価であった当時においてラマヌジャンは主に石板(とチョーク)を用いて試行錯誤に耽っており、気に入った結果だけをルーズリーフに書き起こしていました。ラマヌジャンがハーディに招待されてイギリスに渡る以前に綴じられた三冊のノートブックを"Ramanujan's Notebook"、その後病に伏しインドに帰ってから書かれたテキストの寄せ集めを"Ramanujan's Lost Notebook"と言います。それらのスキャンされたデータ(をさらにスキャンしたもの)はこちらのサイトで閲覧することができます(Go to page numberの右にある>>からpdfに飛べます)。
　依然ラマヌジャンがどのような試行錯誤を経て多くの結果を得たのかを知ることはできませんが、彼のノートブックを見ることでどのような思考の流れがあったのかを推察することくらいはできます。

ラマヌジャンの円周率公式、再び

　例えばラマヌジャンが円周率公式を発見する前後ではどのような思考があったのか見てみましょう。

円周率公式についての記述

　私が軽く目を通した限りだと、まずNotebook 2の終わり際に $s = 2$ の円周率公式が確認できました。
Notebook 2より
このページに
$\begin{aligned} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} (4 x (1 - x))^{n} & = z^{2} \\ \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{3}}{(1)_{n}^{3}} (3 n + 1) (4 x (1 - x))^{n} & = \frac{1}{1 - 2 x} (1 - 24 \sum_{n = 1}^{\infty} \frac{n}{e^{2 n y} - 1}) \end{aligned}$
という公式があることからラマヌジャンは何の脈絡もなく円周率公式を思い付いた、というわけではなさそうに見えます。
　次に円周率公式が現れるのはNotebook 3の中頃あたりになります。
Notebook 3より
これの直前のページを眺めてみると
$\begin{aligned} e^{π \sqrt{22}} & = 2508951.9982 \dots \\ e^{π \sqrt{37}} & = 199148647.999978 \dots \\ e^{π \sqrt{58}} & = 24591257751.99999982 \dots \end{aligned}$
といった公式が、また直後のページを眺めてみると
$\begin{aligned} 2 (1 - 24 \sum_{n = 1}^{\infty} \frac{n q^{4 n}}{1 - q^{4 n}}) - (1 - 24 \sum_{n = 1}^{\infty} \frac{n q^{2 n}}{1 - q^{2 n}}) & = \frac{4 K L}{π^{2}} (k^{'} + l) \\ 4 (1 - 24 \sum_{n = 1}^{\infty} \frac{n q^{8 n}}{1 - q^{8 n}}) - (1 - 24 \sum_{n = 1}^{\infty} \frac{n q^{2 n}}{1 - q^{2 n}}) & = \frac{12 K L}{π^{2}} (\sqrt{k^{'}} + \sqrt{l})^{2} \end{aligned}$
という公式が確認できます。これらの公式もまた円周率公式の核心に迫るものであり、こうしてみるとやはりラマヌジャンには最初から円周率公式に至る道筋が見えていたのではないかと思えます。
　ちなみに前者の公式は
$\begin{aligned} e^{π \sqrt{22}} & ≒ 2^{8} \cdot 99^{2} - 104 \\ e^{π \sqrt{37}} & ≒ 2^{8} \cdot 882^{2} + 104 \\ e^{π \sqrt{58}} & ≒ 2^{8} \cdot 99^{4} - 104 \end{aligned}$
と書き換えることができ、これらの値は円周率公式の指数部分と深い関わりを持っています。

モジュラー方程式についての記述

　ここで出てきた楕円積分、アイゼンシュタイン級数、そして $e^{π \sqrt{N}}$ の近似値などと円周率公式はモジュラー方程式という概念によって深く結びついています。モジュラー方程式についてはラマヌジャンも幾度となく考察している対象であり、ノートブックの至る所に円周率公式にも繋がる重要な記述が見受けられます。
　例えば円周率公式が初めて現れたあたりから少し遡ると $G_{37} = (\sqrt{37} - 6)^{6}$ などを筆頭とした重要な定数が記されているのが確認できます。
Notebook 2より
　さらにNotebook 1まで遡ると316ページ(下の画像右)に(少し掠れて見えづらいですが) $g_{58} = \sqrt{\frac{5 + \sqrt{29}}{2}}$ を筆頭とした同様の定数が確認できます。
Notebook 1より
　興味深いことにNotebook 1の312ページ(画像左)には円周率公式
$\begin{aligned} \frac{1}{π} & = \frac{\sqrt{3}}{6} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{4})_{n} (\frac{3}{4})_{n}}{(1)_{n}^{3}} \frac{8 n + 1}{3^{2 n}} \\ = \frac{2 \sqrt{2}}{3^{2}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{4})_{n} (\frac{3}{4})_{n}}{(1)_{n}^{3}} \frac{10 n + 1}{3^{4 n}} \\ = \frac{\sqrt{11}}{198} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{4})_{n} (\frac{3}{4})_{n}}{(1)_{n}^{3}} \frac{280 n + 19}{99^{2 n}} \\ = \frac{2 \sqrt{2}}{99^{2}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n} (\frac{1}{4})_{n} (\frac{3}{4})_{n}}{(1)_{n}^{3}} \frac{26390 n + 1103}{99^{4 n}} \end{aligned}$
の指数部分に現れる定数に関する表
$\begin{aligned} 3 & - 3 \\ 5 & - 9 \\ 11 & - 99 \\ 29 & - 99^{2} \end{aligned}$
が記されています。

アイゼンシュタイン級数についての記述

　また $G_{37} = (\sqrt{37} - 6)^{6}$ という定数が出てくる少し前のページを眺めているとアイゼンシュタイン級数に関する次ような記述が確認できます。

Notebook 2より

$1 - \frac{3}{y} - 24 \sum_{n = 1}^{\infty} \frac{n}{e^{2 n y} - 1}$
is a complete series which when divided by $z^{2}$ can be expressed as radicals precisely, in the same manner as the series
$1 + 240 \sum_{n = 1}^{\infty} \frac{n^{3}}{e^{2 n y} - 1}$
and the series
$1 - 504 \sum_{n = 1}^{\infty} \frac{n^{5}}{e^{2 n y} - 1}$
when divided by $z^{4}$ and $z^{6}$ respectively.

　これは私の読みが間違っていなければ次のようなことを主張しているものだと思います。

　 $τ = i K^{'} / K = \sqrt{- N}$ においてアイゼンシュタイン級数
$E_{2} (τ) - \frac{3}{π Im (τ)}, E_{4} (τ), E_{6} (τ)$
はそれぞれ $(2 K / π)^{2}, (2 K / π)^{4}, (2 K / π)^{6}$ で割ったとき代数的数となる。

　この主張やその後にも考察されている
$N (1 - 24 \sum_{n = 1}^{\infty} \frac{n}{e^{2 N n y} - 1}) - (1 - 24 \sum_{n = 1}^{\infty} \frac{n}{e^{2 n y} - 1}) = ϕ (e^{- y})^{2} ϕ (e^{- N y})^{2} f (α, β)$
といった形の公式は上でも触れたように円周率公式の導出において最も重要な事実となっています。

超幾何関数についての記述

　この時点でラマヌジャンは円周率公式を発見できるだけの駒をかなり手にしていたわけですが、その直後には王手をかけるように超幾何関数の変換について考察しているのが確認できます。

Notebook 2より

　ここには次のような変換公式が記されています。
$\begin{aligned} \sum_{n = 0}^{\infty} \frac{(\frac{1}{3})_{n} (\frac{2}{3})_{n}}{(1)_{n}^{2}} β^{n} & = \frac{1 + p + p^{2}}{\sqrt{1 + 2 p}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{2}}{(1)_{n}^{2}} α^{n} & (α = \frac{p^{3} (2 + p)}{1 + 2 p} & β = \frac{27}{4} \frac{(p + p^{2})^{2}}{(1 + p + p^{2})^{3}}) \\ \sum_{n = 0}^{\infty} \frac{(\frac{1}{4})_{n} (\frac{3}{4})_{n}}{(1)_{n}^{2}} x^{2 n} & = \frac{1}{\sqrt{1 + x}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{2}}{(1)_{n}^{2}} {(\frac{2 x}{1 + x})}^{n} \\ \sum_{n = 0}^{\infty} \frac{(\frac{1}{6})_{n} (\frac{5}{6})_{n}}{(1)_{n}^{2}} x^{n} & = \sqrt[4]{1 - y + y^{2}} \sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{2}}{(1)_{n}^{2}} y^{n} & (y = \frac{p (2 + p)}{1 + 2 p} & x = \frac{27}{4} \frac{(p + p^{2})^{2}}{(1 + p + p^{2})^{3}}) \end{aligned}$
これは上で触れた
$\sum_{n = 0}^{\infty} \frac{(\frac{1}{2})_{n}^{2}}{(1)_{n}^{2}} k^{2 n} = m_{s} \sum_{n = 0}^{\infty} \frac{(\frac{1}{s})_{n} (1 - \frac{1}{s})_{n}}{(1)_{n}^{2}} k_{s}^{2 n}$
という形の変換公式に他なりません。

まとめ

　以上、ラマヌジャンの論文とノートブックを簡単に眺めてきたわけですが、つまるところ、ええと、ラマヌジャンは全て理解したうえで円周率公式を発見していたことになりませんか？それはそれで怖いですね。

おわりに

　私はついこの間までラマヌジャンの円周率公式について勉強しており、先日ようやくその結果をまとめた記事を公開するに至りました。そうして円周率公式への探究に一息ついたところで「ラマヌジャン、公式だけ暗記してタイムスリップしてきた未来人説」的なツイートがバズっているのを目にしました。それは定期的にバズる内容のものなのでまたいつものかと思っていましたが、昔よりラマヌジャンへの造詣が深まった今、そのツイートの周辺で語られているラマヌジャンの人物像に違和感があることに気付きました。
　この記事はその違和感の正体を確かめるべく書き始めたものなのですが、調べてみれば調べてみるほどラマヌジャンは世間で語られているほどものを知らなかったわけではないことがわかり、むしろ円周率公式周りの理論については知りすぎていて怖くなるほどでした。ラマヌジャンは一体どこからどこまで見透かしていたのでしょうね。
　とりあえず皆さんに知ってもらいたいことは「ラマヌジャンの円周率公式は何の脈絡もなく発見されたものではなく、彼はそれに至る道を既に切り拓いていた」ということにあります。しかし「ラマヌジャンがそのそれぞれの道をどうやって開拓したのか」という部分については謎が多いままであることにも注意したいところです。再三になりますがやはり彼が人間離れした洞察力を持っていたことは確かであり、その根底にある理屈は我々が簡単に理解できるものではないということは依然変わりないと思います。
　最後に私がラマヌジャンのノートブックを眺めていて言葉を失ったページを紹介して終わりといたしましょう。
Notebook 3より

このページについての解説

　この記事に対する多くの反響があった中で、「この最後のページについて解説してほしい」という声がいくつか見られたので私なりの見解を簡単に述べておきます。
　下部の掠れて読めない部分については図書館で原典を確認してみたところ
$\begin{aligned} \sqrt[3]{2} & = 1.259921, 049894, 873164, 767208 \\ = \frac{5}{4} {(1 + \frac{24}{1000})}^{\frac{1}{3}} = \frac{63}{50} {(1 + \frac{188}{1000000})}^{- \frac{1}{3}} \end{aligned}$
と書いてありました。この等式についてはもはや「はいはい、ラマヌジャン、ラマヌジャン」としか言えることはありません(ちなみにこの近似値 $\sqrt[3]{2} = \dots, 767208 \dots$ は正確には $\sqrt[3]{2} = \dots, 76721060 \dots$ と続きます)。
　私が真に言葉を失ったのは、言うまでもなく、上部の四乗和・五乗和の等式にあります。まずもって
$29^{5} = 20511149$
などの値を平気で扱っているのもおかしな話ではあるのですが、たとえ $1$ から順に $4$ 乗、 $5$ 乗の値を書き並べたとして果たして
$4^{4} + 6^{4} + 8^{4} + 9^{4} + 14^{4} = 15^{4}$
や
$5^{5} + 10^{5} + 11^{5} + 16^{5} + 19^{5} + 29^{5} = 30^{5}$
といった関係が簡単に浮かび上がってくるものでしょうか。
　またこのような四乗和の関係式をたった $8$ 本見つけただけで果たして
$\begin{aligned} (8 s^{2} + 40 s t - 24 t^{2})^{4} + (6 s^{2} - 44 s t - 18 t^{2})^{4} + (14 s^{2} - 4 s t - 42 t^{2})^{4} \\ + (9 s^{2} + 27 t^{2})^{4} + (4 s^{2} + 12 t^{2})^{4} & = (15 s^{2} + 45 t^{2})^{4} \\ (4 m^{2} - 12 n^{2})^{4} + (3 m^{2} + 9 n^{2})^{4} + (2 m^{2} - 12 m n - 6 n^{2})^{4} \\ + (4 m^{2} + 12 n^{2})^{4} + (2 m^{2} + 12 m n - 6 n^{2})^{4} & = (5 m^{2} + 15 n^{2})^{4} \end{aligned}$
という一般化を $2$ 本も思い付くことができるでしょうか。
　また興味深いことに"Ramanujan's Notebook Part IV"のp.95にてBerndtはこれらの公式を次のように解説しています。

　一つ目の公式
$\begin{aligned} (8 s^{2} + 40 s t - 24 t^{2})^{4} + & (6 s^{2} - 44 s t - 18 t^{2})^{4} + (14 s^{2} - 4 s t - 42 t^{2})^{4} \\ + (9 s^{2} + 27 t^{2})^{4} + (4 s^{2} + 12 t^{2})^{4} = (15 s^{2} + 45 t^{2})^{4} \end{aligned}$
は既にC. B. Haldeman(1904)にて発見されていた。注目すべきことにラマヌジャンの記した公式はHaldemanの記した公式と記号や項の順番に至るまでもが全く一致しているのだ！ある人は「ラマヌジャンはHaldemanの論文、またはその二次的な文献を見たことがあったのだろう」と結論付けるだろう。しかしその可能性は非常に低いと思われる。なぜならばラマヌジャンがインドで閲覧できた学術誌は非常に少なく、またHaldemanの論文はかなりマイナーな学術誌に掲載されていたのだ。そしてまたラマヌジャンはHaldemanよりも先に上の公式を発見していた、という可能性も十分にある。したがってラマヌジャンとHaldemanが全く同じ公式を記していたのは驚くほど(amazingly)偶然であっただけに違いないだろう。
　また二つ目の公式
$\begin{aligned} (4 m^{2} - 12 n^{2})^{4} + (3 m^{2} + 9 n^{2})^{4} + (2 m^{2} - 12 m n - 6 n^{2})^{4} \\ + (4 m^{2} + 12 n^{2})^{4} + (2 m^{2} + 12 m n - 6 n^{2})^{4} & = (5 m^{2} + 15 n^{2})^{4} \end{aligned}$
についてもHaldeman(1904)にて既に発見されており、同時期にA. Martin(1904)でも証明されている。こちらの公式の表示についてはHaldemanとは異なるのに対し、Martinの記したものとは一致している。これもまた驚くべき(astonishing)偶然に他ならないだろう。

　この記事で考察してきたような解析的な議論に関してはラマヌジャンもある程度の蓄積があったと考えられましたが、タクシー数の逸話やこの四乗和の関係式にも見られるようにラマヌジャンの整数に関するセンスについてはそのような説明が効かず、まさに神懸りであったと言えます。このセンスの鋭さをよく言い表した名言を一つ最後に紹介しておきましょう。

　"Every positive integer is one of Ramanujan's personal friends." - J. E. Littlewood

　では。

おまけ：関連書籍の紹介

　上でも紹介したようにラマヌジャンは1000ページを超える紙の上にひたすら数式を書き起こしていました。その途方もないほどの発見は偉大なるB. C. Berndtによって解読が試みられ、その結果は"Ramanujan's Notebooks (Part I-V)"および"Ramanujan's Lost Notebook (Part I-V)"にまとめられています(最終巻の出版が2018年とかなり最近で驚いています)。これらはラマヌジャンが一体どういったことを書き留め、どういったことを発見したのか詳しく知るには欠かせない十冊となっています。ちなみにBerndtはラマヌジャンの業績に触れて「ラマヌジャンは自身が発見した事実のほとんどに対して証明を付けることができたが、あえてそれをしなかったのではないか」と評しています。
　またP. K. Srinivasanによって蒐集されたラマヌジャンに関する手紙の数々はBerndtらによって"Ramanujan: Letters and Commentary"にて注釈付きでまとめられており、これについては偉大なる細川尋史氏による邦訳"ラマヌジャン書簡集"が出ています。「自己紹介をさせてください」から始まるラマヌジャンの周辺で行われた生のやり取りが歴史的・数学的背景の詳細な解説とともに記録された貴重な一冊となっています。私はまだ初めの方しか読めていませんが、ラマヌジャンがハーディに宛てた二本目の手紙に見られる「私はすでに半分餓死しそうな男であります」や「証明方法を墓の中まで持っていくつもりは決してございません」という言葉がお気に入りです。

追記

　先日調べ物をしていたら上に挙げた書籍の一部
・ Ramanujan's Notebooks Part I
・ Ramanujan's Notebooks Part II
・ Ramanujan's Notebooks Part III
・ Ramanujan's Lost Notebook Part I
・ Ramanujan: Letters and Commentary
がInternet Archiveに挙がっているのを見つけました。
　興味があれば是非ラマヌジャンの業績を目で見て感じてみてはいかがでしょうか。