xy平面上の関数をX(x)Y(y)平面に写す操作である再スケールの定義とX(x)Y(y)平面上の微積分の定義
はじめに
この記事は私が再スケールについて書いた2個目の記事です. 1個目から読みたい人は
超微分の図形的意味から平面上の「再スケール」を定義を考える
を読んでください.
この記事の目的は再スケールという操作と再スケールした平面上における微積分を定義することです.
マクロ
$\rsc$: \rsc$\to$\mathrm{Rsc}
$\rscint$: \rscint$\to$\displaystyle\hspace{0.28em}\mathcal{S}\hspace{-0.95em}\int
再スケールの着想の元: 超微分とは
超微分は7777777氏による微分の定義式のハイパー演算子(足し算$\to$掛け算$\to$冪乗$\to$テトレーション$\to\cdots$)を上げた式によって定義される分野です.
微分導関数の定義式
$$
\frac{d}{dx}f(x):=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}
$$
のハイパー演算子を上げた超微分の定義式は
$$
f^‘(x):=\lim_{h\to 1} \log_h\frac{f(hx)}{f(x)}=\frac{x f'(x)}{f(x)}
$$
となります.
同氏の記事 超微分に関する先行研究 では, 超微分の図形的意味として両対数グラフの接線であることが述べられています. この両対数グラフは平面の各軸に$e^x,\,e^y=\cdots,\,1/e^2,\,1/e,\,0,\,e,\,e^2,\,\cdots$を均等に取った平面上に写された関数です.
再スケール微分は
$$
f(x)=\cdots,\,f(-2),\,f(-1),\,f(0),\,f(1),\,f(2),\,\cdots
$$
$$
g(x)=\cdots,\,g(-2),\,g(-1),\,g(0),\,g(1),\,g(2),\,\cdots
$$
を各軸に均等に取った平面に$xy$平面上で表される関数を写し, 写した関数を微分する操作を意味します.
超微分に興味のある方はここのリンクから相関図が見られます.
超微分の記事まとめ
, 7777777
再スケール
定義
$X:A_X\to B_X,\,Y:A_Y\to B_Y$は定義域内で連続かつ全単射な2関数とする.
関数$f: C\to D\times F\subseteq B_X\times B_Y,\,t\mapsto(x(t),\,y(t))$に対して, $f_{\rsc(X,\,Y)}$を
$$
f_{\rsc(X,\,Y)} (t):=\left\{\begin{array}{l}
X^{-1}(x(t))\\
Y^{-1}(y(t))
\end{array}\right.
$$
と定め, この操作を再スケールと言い, $\rsc$をスケール, スケールの対象になる関数を元または要素と言う.
定義域内連続かつ全単射の2関数を$X:A_X\to B_X,\,Y:A_Y\to B_Y$とする.
関数$f$は定義域内の端点を除いた任意の点で微分可能な関数$f:C\to D,\,x\mapsto f(x)\quad(C\subseteq B_X,\,D\subseteq B_Y)$とする.
$f_{\rsc(X,\,Y)}(x):=(Y^{-1}\circ f\,\circ X)(x)$
陽関数の再スケールの定義は媒介変数表示の再スケールを変形して求められる.
グラフの書き方
$f_{\rsc(X,\,Y)}$の定義の見た目通り, $x,\,y$の方向にそれぞれ$X,\,Y$の逆関数を加えて, 圧縮または伸張してしています. 再スケール後の関数がどうなったか見るために必要なグラフの書き方を教えます.
軸の書き方
$(X,\,Y)=(f,\,g)$としたとき,
横の軸は右から左に$\cdots,\,f(-2),\,f(-1),\,f(0),\,f(1),\,f(2),\,\cdots$
縦の軸は下から上に$\cdots,\,g(-2),\,g(-1),\,g(0),\,g(1),\,g(2),\,\cdots$
を等間隔で刻み, 原点を$(f(0),\,g(0))$とします.
 f(x)g(y)平面
f(x)g(y)平面
関数の書き込み方
関数$h$を再スケールして, $h_{\rsc(f,\,g)}$を計算する.
このとき, $h_{\rsc(f,\,g)}$の書き方は簡単です. $h_{\rsc(f,\,g)}$を$xy$平面と同じときのようにそのまま書いてください.
例題
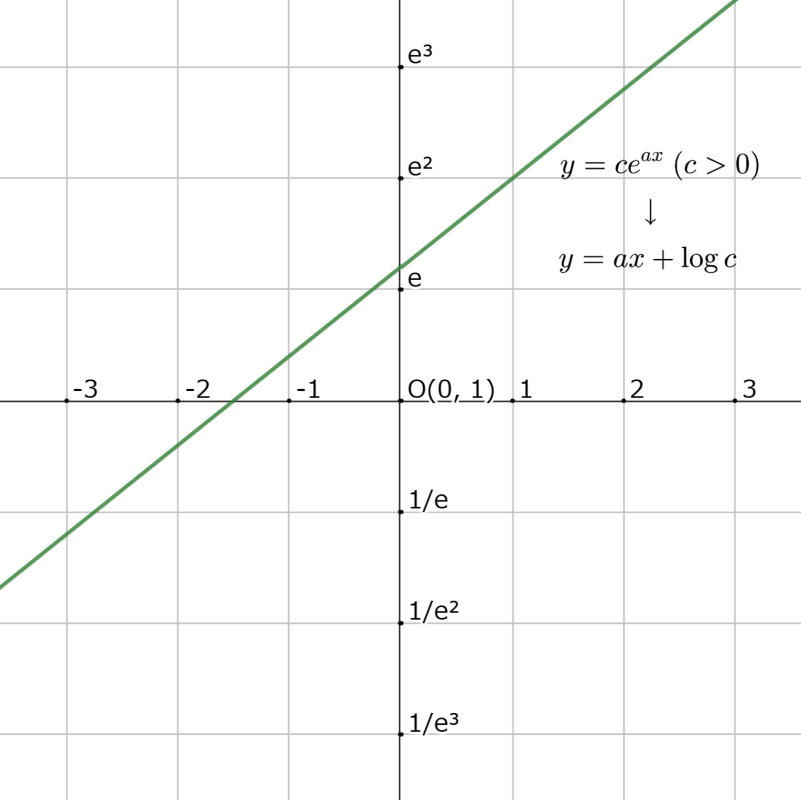
$X\equiv x,\,Y\equiv\exp y$のとき, $f(x)=ce^{ax}\,(c>0)$を$\rsc(X,\,Y)$で再スケールして, $XY$平面上での$f$のグラフを書け.
$X:\mathbb{R}\to\mathbb{R},\,Y:\mathbb{R}\to(0,\,\infty),\,f:\mathbb{R}\to(0,\,\infty)$より, 定義に沿って計算すると
$$
f_{\rsc(X,\,Y)}=\log f(x)=ax+\log c
$$
定理
$X:A_X\to B_X,\,Y:A_Y\to B_Y$は定義域内で連続かつ全単射な2関数とする.
関数$f: C\to D\times F\subseteq B_X\times B_Y,\,t\mapsto(x(t),\,y(t))$に対して, 関数$g$を
$$
g(t)=f_{\rsc(X,\,Y)}(t)
$$
とすると, 次が成り立つ.
$$
g_{\rsc(X^{-1},\,Y^{-1})}=f(t)
$$
$X,\,Y$の逆関数を元に取るスケール$\rsc(X^{-1},\,Y^{-1})$を逆スケールと言い, $\rsc(X^{-1},\,Y^{-1})=\rsc(X,\,Y)^{-1}$と表す.
$X:A_X\to B_X,\,Y:A_Y\to B_Y$は定義域内で連続かつ全単射な2関数とする.
関数$f: C\to D\times F\subseteq B_X\times B_Y,\,t\mapsto(x(t),\,y(t))$に対して, 関数$g$を次のように置く.
$$
g(t)=f_{\rsc(X,\,Y)} (t)=\left\{\begin{array}{l}
X^{-1}(x(t))\\
Y^{-1}(y(t))
\end{array}\right.
$$
このとき, $g_{\rsc(X^{-1},\,Y^{-1})} (t)$を定義より計算すると
$$
g_{\rsc(X^{-1},\,Y^{-1})} (t)=\left\{\begin{array}{l}
X(X^{-1}(x(t)))\\
Y(Y^{-1}(y(t)))
\end{array}\right.
=\left\{\begin{array}{l}
x(t)\\
y(t)
\end{array}\right.
=f(t)
$$
関数$X_1,\,X_2,\,Y_1,\,Y_2$を定義域内で連続かつ全単射とし, 関数$f$は定義域内で連続な関数とする. $X_1(x)=X_2(-x),\,Y_1(x)=Y_2(-x)$を満たすとき, 次が成り立つ.
- $\!X$軸対称: $f_{\rsc(X_1,\,Y_1)}(x)=-f_{\rsc(X_1,\,Y_2)}(x)$
- $\!Y$軸対称: $f_{\rsc(X_1,\,Y_1)}(x)=f_{\rsc(X_2,\,Y_1)}(-x)$
- 原点対称: $f_{\rsc(X_1,\,Y_1)}(x)=-f_{\rsc(X_2,\,Y_2)}(-x)$
$\!X$軸対称
$$ Y_1(x)=Y_2(-x)\Leftrightarrow x=Y_2(-Y_1^{-1}(x))\Leftrightarrow Y_1^{-1}(x)=-Y_2^{-1}(x) $$
より
$$ f_{\rsc(X_1,\,Y_1)}(x)=Y_1^{-1}(f(X_1(x)))=-Y_2^{-1}(f(X_1(x)))=-f_{\rsc(X_1,\,Y_2)}(x) $$
である.$\!Y$軸対称
$$ f_{\rsc(X_1,\,Y_1)}(x)=Y_1^{-1}(f(X_1(x)))=Y_1^{-1}(f(X_2(-x)))=-f_{\rsc(X_2,\,Y_1)}(-x) $$
である.原点対称
$\!X$軸対称と$\!Y$軸対称の変形を順に使えば求める関係式が得られる.
再スケール微分
定義域内連続かつ全単射かつ微分可能な2関数を$X:A_X\to B_X,\,Y:A_Y\to B_Y$とする.
関数$f:C\to D,\,x\mapsto f(x)\quad(C\subseteq B_X,\,D\subseteq B_Y)$とする.
$a\in C$に対して
$$
f_{\nabla\rsc(X,\,Y)}(a):=\lim_{h\to 0} \frac{(Y^{-1}\circ f\,\circ X)(X^{-1}(a)+h)-(Y^{-1}\circ f\,\circ X)(X^{-1}(a))}{h}
$$
と定める.
これを$f$のスケール$\rsc(X,\,Y)$に対する$x=a$における再スケール微分係数と言い, $f_{\rsc(X,\,Y)}$は$a$で狭義再スケール微分可能と言う.
また, これを形式的に次の記号で表す.
$$
\frac{d}{d_{\rsc(X,\,Y)}x}f(a)=f_{\nabla\rsc(X,\,Y)}(a)
$$
定義域内連続かつ全単射かつ微分可能な2関数を$X:A_X\to B_X,\,Y:A_Y\to B_Y$とする.
関数$f:C\to D,\,x\mapsto f(x)\quad(C\subseteq B_X,\,D\subseteq B_Y)$とする.
$x\in C$に対して
$$
f_{\nabla\rsc(X,\,Y)}(x):=\lim_{h\to 0} \frac{(Y^{-1}\circ f\,\circ X)(X^{-1}(x)+h)-(Y^{-1}\circ f\,\circ X)(X^{-1}(x))}{h}
$$
と定める.
これを$f$のスケール$\rsc(X,\,Y)$に対する再スケール導関数と言う.
また, これを形式的に次の記号で表す.
$$
\frac{d}{d_{\rsc(X,\,Y)}x}f(x)=f_{\nabla\rsc(X,\,Y)}(x)
$$
$X,\,Y,\,f$が定義域内で微分可能$\Rightarrow f$は定義域内でスケール$\rsc(X,\,Y)$に対する再スケール微分可能
再スケール微分の変換公式
$f$が$x\in C$で微分可能であるとき
$$
f_{\nabla\rsc(X,\,Y)}(x)=\frac{f'(x)(\frac{d}{dx}Y^{-1}\circ f)(x)}{\frac{d}{dx}X^{-1}(x)}
$$
変換公式から分かる通り, 関数の和や積についての再スケール微分は関数$Y$の性質によって簡単にできるかどうかが変わります.
再スケール微分の定義は
$$
f_{\nabla\rsc(X,\,Y)}(x)=\lim_{h\to 0} \frac{(Y^{-1}\circ f\,\circ X)(X^{-1}(x)+h)-(Y^{-1}\circ f\,\circ X)(X^{-1}(x))}{h}
$$
である.
$$
f_{\nabla\rsc(X,\,Y)}(x)=\frac{d}{dt}(Y^{-1}\circ f\,\circ X)(t)\Bigg|_{t=X^{-1}(x)}
$$
$$
=\left\{\left(\frac{dY^{-1}}{dt}\circ f\,\circ X\right)(t)\cdot\left(\frac{df}{dt}\,\circ X\right)(t)\cdot\frac{dX}{dt}\right\}\Bigg|_{t=X^{-1}(x)}
$$
$$
=\left(\frac{dY^{-1}}{dx}\circ f\right)(x)\cdot\frac{df}{dx}\cdot\left(\frac{dX}{dx}\circ X^{-1}\right)(x)
$$
合成関数の微分より, $X(X^{-1}(x))=x$を微分して
$$
\frac{dX}{dx}(X^{-1}(x))\cdot\frac{dX^{-1}}{dx}=1\Leftrightarrow\frac{dX}{dx}(X^{-1}(x))=\frac{1}{\frac{dX^{-1}}{dx}}
$$
となるので
$$
f_{\nabla\rsc(X,\,Y)}(x)=\frac{f'(x)(\frac{d}{dx}Y^{-1}\circ f)(x)}{\frac{d}{dx}X^{-1}(x)}
$$
次のスケール$\rsc(X,\,Y)$について, 再スケール導関数$f_{\nabla\rsc(X,\,Y)}(x)$を変換公式に当てはめて等式を求めよ.
$X(x)=ae^{bx}, Y(y)=pe^{qy}\,(a,\,b,\,p,\,q\in\mathbb{R},\,0< a,\,p)$
変換公式にそのまま代入して
$$
f_{\nabla\rsc(X,\,Y)}(x)=\dfrac{f'(x)(\frac{d}{dx}\frac{1}{q}(\log x-\log p)\circ f)(x)}{\frac{d}{dx}\frac{1}{b}(\log x-\log a)}=\dfrac{bxf'(x)}{qf(x)}
$$
再スケール積分
定義
基本は合成関数の積分なのですが, 一応定義しときましょう.
定義域内連続かつ全単射な2関数を$X:A_X\to B_X,\,Y:A_Y\to B_Y$とする.
$f:C\to D,\,x\mapsto f(x)\quad(C\subseteq B_X,\,D\subseteq B_Y)$は定義域内で連続とする.
方針
$xy$平面の$f$を$XY$平面に写した$f_{\rsc(X,\,Y)}$を通常の積分の定義と同様にRiemann和で上下で面積を挟むことで定義する.
閉区間$I=[a,\,b]\subseteq C$の分割$\Delta=\{I_k\}_{1\leq k\leq n}$を
$$
\Delta:a=x_0< x_1<\cdots< x_n=b,\,I_k=[x_{k-1},\,x_k]_{1\leq k\leq n}
$$
とする.
$Y$が広義単調増加の場合
$Y$は全単射なので, 単調性が言える. まず, $Y$が広義単調増加の場合で定義を考える.
過剰再スケール和$R(f,\,\Delta)$, 不足再スケール和$r(f,\,\Delta)$を次のように定義する.
$$
R(f,\,\Delta):=Y\left(\sum_{k=1}^n \;\sup\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
$$
$$
r(f,\,\Delta):=Y\left(\sum_{k=1}^n \;\inf\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
$$
$f:C\subseteq B_X\to D\subseteq B_Y$が有界であるとき
$$
\overline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x:=\inf_\Delta\;R(f,\,\Delta)
$$
$$
\underline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x:=\sup_\Delta\;r(f,\,\Delta)
$$
が存在して, それぞれ上再スケール積分, 下再スケール積分とする. (スケールが自明な場合は${\rsc(X,\,Y)}$を省略する.)
$$
\underline{\rscint_a^b} f(x)\,dx\leq\overline{\rscint_a^b} f(x)\,dx
$$
が常に成り立つ.
2の補題4.1, 系4.2の証明を参考に有界性の証明と不等式の証明をする.
$I=[a,\,b]$とし, $I$の分割を$I_k=[a_{k-1},\,a_k],\,J_l=[b_{l-1},\,b_l],\,\Delta:=\{I_k\}_{1\leq k\leq n},\,\Delta':=\{J_l\}_{1\leq l\leq m}$とする.
任意の$1\leq k\leq n$に対して, $\inf\{f(x)\mid x\in I_k\}\leq\sup\{f(x)\,|\,x\in I_k\}$である.
$$
\inf\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\leq\sup\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|
$$
$$
\sum_{k=1}^n \inf\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\leq\sum_{k=1}^n \sup\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|
$$
$Y$は広義単調増加なので, 順序を保ち, 次が成り立つ.
$$
r(f,\,\Delta)\leq R(f,\,\Delta)\cdots\cdots(1)
$$
次に各$k$に対して, $J_l\subset I_k$を満たす任意の$l$を取れば, $r(f,\,I_k)\leq r(f,\,J_l),\,R(f,\,J_l)\leq R(f,\,I_k)$が成り立つ.
$$
\sum_{k=1}^n r(f,\,I_k)|X^{-1}(a_k)-X^{-1}(a_{k-1})|
\leq\sum_{k=1}^n \sum_{l:J_l\subset I_k} r(f,\,J_l)|X^{-1}(b_l)-X^{-1}(b_{l-1})|
=\sum_{l=1}^m r(f,\,J_l)|X^{-1}(b_l)-X^{-1}(b_{l-1})|
$$
$$
\sum_{k=1}^n R(f,\,I_k)|X^{-1}(a_k)-X^{-1}(a_{k-1})|
\geq\sum_{k=1}^n \sum_{l:J_l\subset I_k} R(f,\,J_l)|X^{-1}(b_l)-X^{-1}(b_{l-1})|
=\sum_{l=1}^m R(f,\,J_l)|X^{-1}(b_l)-X^{-1}(b_{l-1})|
$$
よって, 次が成り立つ.
$$
r(f,\,\Delta)\leq r(f,\,\Delta'),\,R(f,\,\Delta')\leq R(f,\,\Delta)\cdots\cdots(2)
$$
$\Delta''=\Delta\cup\Delta'$なる$I$の分割を取ることができ, $(1),\,(2)$より
$$
r(f,\,\Delta)\leq r(f,\,\Delta'')\leq R(f,\,\Delta'')\leq R(f,\,\Delta')
$$
$$
\therefore r(f,\,\Delta)\leq R(f,\,\Delta')
$$
$\Delta'$を固定して, $\Delta$の分割$I_k (1\leq k\leq n)$全体を任意に動かすと
$$
r(f,\,\Delta)\leq\overline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x\leq R(f,\,\Delta')
$$
ここから$\Delta'$の分割$I_l (1\leq l\leq m)$全体を任意に動かすと
$$
r(f,\,\Delta)\leq\underline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x\leq\overline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x\leq R(f,\,\Delta')
$$
となり, 有界性と不等式を得られた.
$$
\overline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x=\underline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x
$$
が成り立つとき, $f$は$[a,\,b]$上で再スケール積分可能(または再スケール可積分)と言い
$$
\rscint_a^b f(x)\,d_{\rsc(X,\,Y)}x:=\overline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x=\underline{\rscint_a^b} f(x)\,d_{\rsc(X,\,Y)}x
$$
を$f$の再スケール定積分と言う.
(スケールが自明な場合は${\rsc(X,\,Y)}$を省略する.)
$Y$が広義単調減少の場合
$Y$全単射より$Y_+(y)=Y(-y)$なる$Y_+$が1つ取れる. $Y,\,Y_+$は$xy$平面上の$x$軸で線対称であるから, $Y_+$は広義単調増加である.
$I=[a,\,b]$の分割$\Delta:=\{I_k\}\,(1\leq k\leq n)$を取ると, 各$k$に対して
$\inf\{f(x)\mid x\in I_k\}=-\sup\{-f(x)\mid x\in I_k\},\,\sup\{f(x)\mid x\in I_k\}=-\inf\{-f(x)\mid x\in I_k\}$が成り立つ.
$$
R(f,\,\Delta):=Y\left(\sum_{k=1}^n \;\inf\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
=Y_+\left(\sum_{k=1}^n \;\sup\{-f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
$$
$$
r(f,\,\Delta):=Y\left(\sum_{k=1}^n \;\sup\{f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
=Y_+\left(\sum_{k=1}^n \;\inf\{-f(x)\mid x\in I_k\}|X^{-1}(x_k)-X^{-1}(x_{k-1})|\;\right)
$$
とおけば, 広義単調増加の再スケール積分を定義しているので, 広義単調減少の再スケール積分を定義できる.
関数$f$が$\rsc(X,\,Y)$に対して, 再スケール積分可能$\Leftrightarrow$任意の$\epsilon>0$に対して, ある$I$の分割$\Delta:=\{I_k\}\,(1\leq k\leq n)$があり, $|R(f,\,\Delta)-r(f,\,\Delta)|<\epsilon$を満たす.
再スケール積分の変換公式
$f$は再スケール可積分とするとき, $f$は積分可能で次が成り立つ.
$$
\rscint f(x)\,d_{\rsc(X,\,Y)}x=Y\left(\int (X^{-1})'(x)f(x)\,dx\right)
$$
再スケール微分の変換公式と同じく再スケール積分の変換公式も, 関数の和や積についての再スケール積分は関数$Y$の性質によって簡単にできるかどうかが変わります.
関数$f:C_f\to D_f,\,g:C_g\to D_g\quad(C_f,\,C_g\subseteq B_X,\,D_f\subseteq A_Y,\,D_g\subseteq B_Y)$は定義域内の端点を除いた任意の点で微分可能とする.
このとき, 次の式を$g(x)$について解きます.
$$
f(x)=g_{\nabla\rsc(X,\,Y)}(x)=\frac{d}{dt}(Y^{-1}\circ g\,\circ X)(t)\bigg|_{t=X^{-1}(x)}
$$
$x$に$X(x)$を代入して
$$
f(X(x))=\frac{d}{dx}(Y^{-1}\circ g\,\circ X)(x)
$$
両辺を積分して
$$
(Y^{-1}\circ g\,\circ X)(x)=\int f(X(x))\,dx
$$
$$
g(x)=Y\left(\int^{X^{-1}(x)} (f\,\circ X)(t)\,dt\right)
$$
さらに$u=X(t)$と置くと, $t=X^{-1}(x)\to u=x$になるので, $u$を$x$の積分に変えて
$$
g(x)=Y\left(\int \frac{f(x)}{X'(X^{-1}(x))}\,dx\right)=Y\left(\int (X^{-1})'(x)f(x)\,dx\right)
$$
を得る.
再スケール微積分の基本定理
$f$は再スケール可積分とするとき, $f$は積分可能で次が成り立つ.
$$
\frac{d}{d_{\rsc(X,\,Y)}x}\rscint f(x)\,d_{\rsc(X,\,Y)}x=f(x)
$$
再スケール積分の変換公式より
$$
\rscint f(x)\,d_{\rsc(X,\,Y)}x=Y\left(\int (X^{-1})'(x)f(x)\,dx\right)
$$
再スケール微分の定義式から
$$
\frac{d}{d_{\rsc(X,\,Y)}x}\rscint f(x)\,d_{\rsc(X,\,Y)}x=\frac{d}{dt} Y^{-1}\left(Y\left(\int^{X(t)} (X^{-1})'(s)f(s)\,ds\right)\right)\Bigg|_{t=X^{-1}(x)}
$$
$$
=\frac{d}{dt} \int^{X(t)} (X^{-1})'(s)f(s)\,ds\Bigg|_{t=X^{-1}(x)}
$$
$u=X^{-1}(s)$と置換すると, $s=X(u)$より$ds=X'(u)\,du$となるから
$$
=\frac{d}{dt} \int^t f(X(u))\,du\Bigg|_{t=X^{-1}(x)}
=f(X(t))\bigg|_{t=X^{-1}(x)}
=f(x)
$$
おわりに
再スケール微分の変換公式, 再スケール積分の変換公式から関数の和や積の再スケール微積分などの性質は$Y$がどんな関数かによって変わり, 関数方程式$f(x+y)=f(x)+f(y)$などを満たす性質がある関数を考える必要があるので, そのことについては次の記事で書きたいと思います.
更新履歴
2024年12月27日: 記事投稿
