文献あり

コーシー列を2重数列の収束と捉える

191

はじめに

距離空間の点列$\seq{x_n}{n}$がコーシー列であることを
$$ \lim_{n,m\to\infty} d(x_n,x_m)=0$$
と書くことがありますが，左辺の極限はどういう意味なのでしょうか．$\varepsilon$-$N$論法を略記した形式的なものと思ってもいいですが，実際にある種の極限として解釈することもできます．
先に結論だけ書くと，$\N\times\N$を直積順序によって有向集合とみなし，$d(x_n,x_m)$をこの有向集合$\N\times\N$によって添字づけられたネットと考えればよいです．このとき$\seq{x_n}{n}$がコーシー列であることは，ネット$\net{d(x_n,x_m)}{\pair{n,m}\in\N\times\N}$が$0$に収束することと同値になります．

距離空間におけるネット

ネットの収束

以下，ネットの上極限・下極限の内容は既知とする．

上極限を使った議論に慣れるため，本記事の証明では敢えて上極限を多用します．
上極限に不慣れな人は，命題1 や命題4 を定義とみなして読み進めることも可能です．（その場合は，上極限を用いた証明を$\varepsilon$-$N$論法的なやり方で書き直してみることをおすすめします．）

このとき実数列の場合と同様に，ネットの収束が次のように定義できる．

距離空間におけるネットの収束

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$が点$x\in X$に収束するとは
$$ \limsup_{\lambda\in\Lambda}d(x_\lambda,x)\le 0$$
が成り立つことをいう．

$\varepsilon$-$N$論法

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$と点$x\in X$について，次の2条件は同値である．

$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に収束する．
各$\varepsilon\in(0,\infty)$に対して「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)< \varepsilon$が成り立つ」という性質を満たす$\lambda\in\Lambda$が存在する．

(1)を言い換えると
\begin{align*} &\limsup_{\lambda\in\Lambda}d(x_\lambda,x)\le 0 \\ \iff&{}^\forall\varepsilon\in(0,\infty),\ \limsup_{\lambda\in\Lambda}d(x_\lambda,x)<\varepsilon \\ % \iff&{}^\forall\varepsilon\in(0,\infty),\ \text{$\varepsilon$ は $\{\sup_{\mu\succeq\lambda}d(x_\mu,x)\mid \lambda\in\Lambda\}$ の下界でない} \\ \iff&{}^\forall\varepsilon\in(0,\infty),\ {}^\exists\lambda\in\Lambda,\ \sup_{\mu\succeq\lambda}d(x_\mu,x)<\varepsilon \end{align*}
であり，$\sup_{\mu\succeq\lambda}d(x_\mu,x)<\varepsilon$であれば「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)< \varepsilon$が成り立つ」という性質が成り立つから，$(1)\Rightarrow(2)$が示された．
逆に(2)のとき，各$\varepsilon\in(0,\infty)$に対して「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)<\varepsilon/2$が成り立つ」という性質を満たす$\lambda\in\Lambda$が取れる．この性質は$\sup_{\mu\succeq\lambda}d(x_\mu,x)\le \varepsilon/2<\varepsilon$を意味するから，冒頭の言い換えより$(2)\Rightarrow(1)$も成り立つ．

極限の一意性

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$が2点$x,y\in X$に収束するならば，$x=y$である．

任意の$\lambda\in\Lambda$に対して$d(x,y)\le d(x_\lambda,x)+d(x_\lambda,y)$が成り立つから
\begin{align*} d(x,y) &\le \limsup_{\lambda\in\Lambda}(d(x_\lambda,x)+d(x_\lambda,y)) \\ &\le \limsup_{\lambda\in\Lambda}d(x_\lambda,x)+\limsup_{\lambda\in\Lambda}d(x_\lambda,y) \\ &\le 0. \end{align*}

収束$\Rightarrow$部分ネットも収束

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$を有向集合，$\pair{X,d}$を距離空間とし，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$と点$x\in X$を考える．
このとき$\net{x_\lambda}{\lambda\in\Lambda}$が$x$に収束するならば，$\net{x_\lambda}{\lambda\in\Lambda}$の任意の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$も$x$に収束する．

$\net{d(x_{\phi(\mu)},x)}{\mu\in M}$は$\net{d(x_\lambda,x)}{\lambda\in\Lambda}$の部分ネットだから
$$ \limsup_{\mu\in M}d(x_{\phi(\mu)},x)\le\limsup_{\lambda\in\Lambda}d(x_\lambda,x)\le 0.$$

直積順序

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$を前順序集合とし，直積集合$\Lambda\times M$上の二項関係$\preceq$を
$$ \pair{\lambda,\mu}\preceq\pair{\lambda',\mu'} \ \Longleftrightarrow\ \lambda\preceq_\Lambda \lambda' \text{ かつ } \mu\preceq_M\mu' \qquad (\pair{\lambda,\mu},\pair{\lambda',\mu'}\in\Lambda\times M)$$
で定める．このとき，次のことが成り立つ．

$\preceq$は$\Lambda\times M$上の前順序である．
$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$がともに有向集合であれば，$\pair{\Lambda\times M,\preceq}$も有向集合である．

この前順序$\preceq$を，$\preceq_\Lambda$と$\preceq_M$の直積順序という．

$\pair{\lambda,\mu},\pair{\lambda',\mu'},\pair{\lambda'',\mu''}\in\Lambda\times M$とする．

- $\lambda\preceq_\Lambda\lambda$と$\mu\preceq_M\mu$が成り立つから，$\pair{\lambda,\mu}\preceq\pair{\lambda,\mu}$である．
- $\pair{\lambda,\mu}\preceq\pair{\lambda',\mu'}\preceq\pair{\lambda'',\mu''}$とする．このとき$\lambda\preceq_\Lambda\lambda'\preceq_\Lambda\lambda''$と$\mu\preceq_M\mu'\preceq_M\lambda''$が成り立つから，$\lambda\preceq_\Lambda\lambda''$かつ$\mu\preceq_M\mu''$，つまり$\pair{\lambda,\mu}\preceq\pair{\lambda'',\mu''}$である．
$\{\lambda,\lambda'\}$の上界$\lambda''\in\Lambda$と$\{\mu\,\mu'\}$の上界$\mu''\in M$を取れば，$\lambda\preceq_\Lambda\lambda''$と$\mu\preceq_M\mu''$より$\pair{\lambda,\mu}\preceq\pair{\lambda'',\mu''}$が，$\lambda'\preceq_\Lambda\lambda''$と$\mu'\preceq_M\mu''$より$\pair{\lambda',\mu'}\preceq\pair{\lambda'',\mu''}$が成り立つから，$\pair{\lambda'',\mu''}$は$\{\pair{\lambda,\mu},\pair{\lambda',\mu'}\}$の上界である．

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$を前順序集合とし，$\preceq$を$\Lambda\times M$上の直積順序とする．このとき，次のことを示せ．

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$がともに半順序集合であれば，$\pair{\Lambda\times M,\preceq}$も半順序集合である．
$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$がともに全順序集合であっても，$\pair{\Lambda\times M,\preceq}$が全順序集合とは限らない．

$\pair{\lambda,\mu},\pair{\lambda',\mu'}\in\Lambda\times M$とする．

解答例
$\pair{\lambda,\mu}\preceq\pair{\lambda',\mu'}$かつ$\pair{\lambda',\mu'}\preceq\pair{\lambda,\mu}$が成り立つとき，$\lambda\preceq_\Lambda\lambda'$かつ$\lambda'\preceq_\Lambda\lambda$より$\lambda=\lambda'$であり，$\mu\preceq_M\mu'$かつ$\mu'\preceq_M\mu$より$\mu=\mu'$だから，$\pair{\lambda,\mu}=\pair{\lambda',\mu'}$が成り立つ．
解答例
$\N$を大小関係によって全順序集合とみなすと，$\pair{0,1}\preceq\pair{1,0}$も$\pair{1,0}\preceq\pair{0,1}$も成り立たないから，$\N\times\N$は直積順序$\preceq$に関して全順序集合でない．

$\pair{\Lambda,\preceq_\Lambda},\pair{\Lambda',\preceq_{\Lambda'}},\pair{M,\preceq_M},\pair{M',\preceq_{M'}}$を前順序集合とし，写像$\phi:\Lambda\to M$と$\phi':\Lambda'\to M'$は次の2条件を満たすとする．

各$\lambda\in\Lambda$に対して「$\nu\succeq_{M}\mu$を満たす任意の$\nu\in M$に対して$\lambda\preceq_{\Lambda}\phi(\nu)$が成り立つ」という性質を満たす$\mu\in M$が存在する．
各$\lambda'\in\Lambda'$に対して「$\nu'\succeq_{M'}\mu'$を満たす任意の$\nu'\in M'$に対して$\lambda'\preceq_{\Lambda'}\phi'(\nu')$が成り立つ」という性質を満たす$\mu'\in M'$が存在する．

このとき，写像$\phi\times\phi':\Lambda\times\Lambda'\ni\pair{\lambda,\lambda'}\mapsto\pair{\phi(\lambda),\phi'(\lambda')}\in M\times M'$も同様の性質：

各$\pair{\lambda,\lambda'}\in\Lambda\times\Lambda'$に対して「$\pair{\nu,\nu'}\succeq\pair{\mu,\mu'}$を満たす任意の$\pair{\nu,\nu'}\in M\times M'$に対して$\pair{\lambda,\lambda'}\preceq(\phi\times\phi')(\nu,\nu')$が成り立つ」という性質を満たす$\pair{\mu,\mu'}\in M\times M'$が存在する．

を満たすことを確かめよ．ただし，$\Lambda\times\Lambda'$と$M\times M'$はそれぞれ直積順序によって前順序集合とみなす．

直積順序の定義より明らか．（仮定と結論を見比べよ．）

コーシーネット

距離空間におけるコーシーネット

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$がコーシーネットであるとは，ネット$\net{d(x_\lambda,x_\mu)}{\pair{\lambda,\mu}\in\Lambda\times\Lambda}$が$0$に収束すること，つまり
$$ \limsup_{\pair{\lambda,\mu}\in\Lambda\times\Lambda}d(x_\lambda,x_\mu)\le 0$$
が成り立つことをいう．ただし，$\Lambda\times\Lambda$は直積順序によって有向集合とみなしている．

上の定義が$\varepsilon$-$N$論法的なコーシーネット（コーシー列）の定義と一致するという次の命題が，本記事の主題である．

$\varepsilon$-$N$論法

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$について，次の2条件は同値である．

$\net{x_\lambda}{\lambda\in\Lambda}$はコーシーネットである．
各$\varepsilon\in(0,\infty)$に対して「$\mu\succeq\lambda$かつ$\nu\succeq\lambda$を満たす任意の$\mu,\nu\in\Lambda$に対して$d(x_\mu,x_\nu)<\varepsilon$が成り立つ」という性質を満たす$\lambda\in\Lambda$が存在する．

$(1)\Rightarrow(2)$：詳細
$\varepsilon\in(0,\infty)$を任意に取ると，「$\pair{\mu,\nu}\succeq\pair{\lambda_1,\lambda_2}$を満たす任意の$\pair{\mu,\nu}\in\Lambda\times\Lambda$に対して$d(x_\mu,x_\nu)<\varepsilon$が成り立つ」という性質を満たす$\pair{\lambda_1,\lambda_2}\in\Lambda\times\Lambda$が取れる．そこで$\{\lambda_1,\lambda_2\}$の上界$\lambda\in\Lambda$を取れば，$\mu\succeq\lambda$かつ$\nu\succeq\lambda$を満たす任意の$\mu,\nu\in\Lambda$に対して$\pair{\mu,\nu}\succeq\pair{\lambda,\lambda}\succeq\pair{\lambda_1,\lambda_2}$より$d(x_\mu,x_\nu)<\varepsilon$が成り立つ．
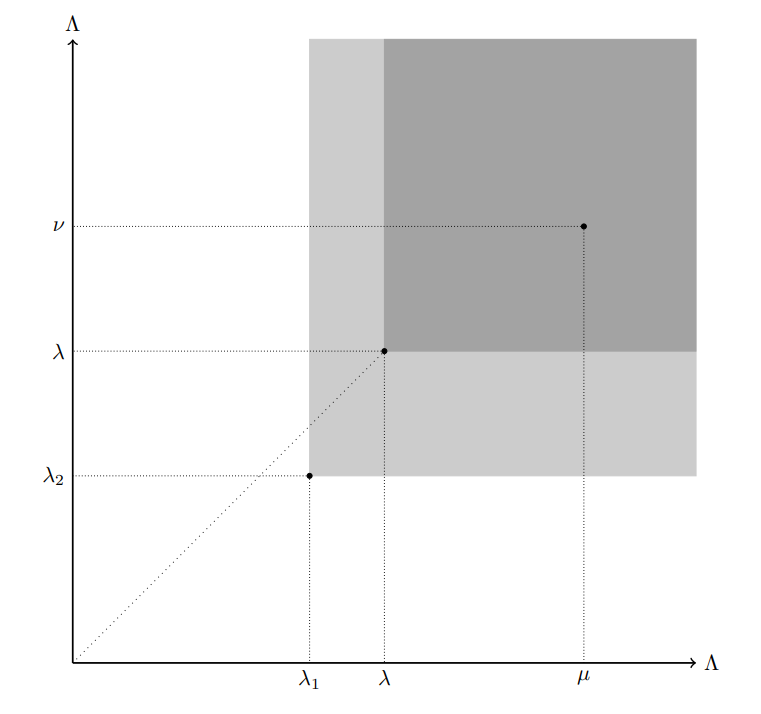
$(2)\Rightarrow(1)$：詳細
$\varepsilon\in(0,\infty)$を任意に取ると，「$\mu\succeq\lambda$かつ$\nu\succeq\lambda$を満たす任意の$\mu,\nu\in\Lambda$に対して$d(x_\mu,x_\nu)<\varepsilon$が成り立つ」という性質を満たす$\lambda\in\Lambda$が取れる．この性質は，$\pair{\lambda,\lambda}$が「$\pair{\mu,\nu}\succeq\pair{\lambda,\lambda}$を満たす任意の$\pair{\mu,\nu}\in\Lambda\times\Lambda$に対して$d(x_\mu,x_\nu)<\varepsilon$が成り立つ」という性質を満たすことを意味している．

コーシーネットに対しても，コーシー列と同様に以下のような性質が成り立っている．

収束ネット$\Rightarrow$コーシーネット

$\pair{\Lambda,\preceq}$を有向集合とし，$\pair{X,d}$を距離空間とする．このとき，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$が点$x\in X$に収束するならば，$\net{x_\lambda}{\lambda\in\Lambda}$はコーシーネットである．

任意の$\lambda,\mu\in\Lambda$に対して$d(x_\lambda,x_\mu)\le d(x_\lambda,x)+d(x_\mu,x)$が成り立つから
\begin{align*} \limsup_{\pair{\lambda,\mu}\in\Lambda\times \Lambda}d(x_\lambda,x_\mu) &\le\limsup_{\pair{\lambda,\mu}\in\Lambda\times \Lambda}(d(x_\lambda,x)+d(x_\mu,x)) \\ &\le\limsup_{\pair{\lambda,\mu}\in\Lambda\times \Lambda}d(x_\lambda,x)+\limsup_{\pair{\lambda,\mu}\in\Lambda\times \Lambda}d(x_\mu,x) \\ &=\limsup_{\lambda\in\Lambda}d(x_\lambda,x)+\limsup_{\mu\in \Lambda}d(x_\mu,x) \\ &\le 0. \end{align*}

コーシーネット$\Rightarrow$部分ネットもコーシーネット

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$を有向集合，$\pair{X,d}$を距離空間とし，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$を考える．
このとき$\net{x_\lambda}{\lambda\in\Lambda}$がコーシーネットであれば，$\net{x_\lambda}{\lambda\in\Lambda}$の任意の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$もコーシーネットである．

問題2 より$\net{d(x_{\phi(\mu)},x_{\phi(\mu')})}{\pair{\mu,\mu'}\in M\times M}$は$\net{d(x_\lambda,x_{\lambda'})}{\pair{\lambda,\lambda'}\in\Lambda\times\Lambda}$の部分ネットだから，$0$に収束する．

コーシーネットが収束部分ネットをもつ$\Rightarrow$収束

$\pair{\Lambda,\preceq_\Lambda}$を有向集合，$\pair{X,d}$を距離空間とし，$X$上のコーシーネット$\net{x_\lambda}{\lambda\in\Lambda}$を考える．
このとき$\net{x_\lambda}{\lambda\in\Lambda}$のある部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$が点$x\in X$に収束するならば，$\net{x_\lambda}{\lambda\in\Lambda}$も$x$に収束する．

問題2 より$\net{d(x_{\lambda},x_{\phi(\mu)})}{\pair{\lambda,\mu}\in \Lambda\times M}$は$\net{d(x_\lambda,x_{\lambda'})}{\pair{\lambda,\lambda'}\in\Lambda\times\Lambda}$の部分ネットだから
\begin{align*} \limsup_{\lambda\in\Lambda}d(x_\lambda,x) &=\limsup_{\pair{\lambda,\mu}\in\Lambda\times M}d(x_\lambda,x) \\ &\le \limsup_{\pair{\lambda,\mu}\in\Lambda\times M}(d(x_\lambda,x_{\phi(\mu)})+d(x_{\phi(\mu)},x)) \\ &\le \limsup_{\pair{\lambda,\mu}\in\Lambda\times M}d(x_\lambda,x_{\phi(\mu)})+\limsup_{\pair{\lambda,\mu}\in\Lambda\times M}d(x_{\phi(\mu)},x) \\ &\le \limsup_{\pair{\lambda,\lambda'}\in\Lambda\times \Lambda}d(x_\lambda,x_{\lambda'})+\limsup_{\mu\in M}d(x_{\phi(\mu)},x) \\ &\le 0. \end{align*}

完備距離空間（復習）

距離空間$\pair{X,d}$が（点列）完備であるとは，$X$上の任意のコーシー列が，$X$のある点に収束することをいう．

$\pair{\Lambda,\preceq}$を有向集合，$\pair{X,d}$を完備距離空間とし，$X$上のコーシーネット$\net{x_\lambda}{\lambda\in\Lambda}$を考える．
このとき，ある点$x\in X$が存在して，$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に収束する．

$\Lambda$上の二項演算$\vee$であって，すべての$\lambda,\lambda'\in\Lambda$に対して$\lambda\preceq\lambda\vee\lambda'$かつ$\lambda'\preceq\lambda\vee\lambda'$を満たすものを$1$つ固定する．さて，$\net{x_\lambda}{\lambda\in\Lambda}$はコーシーネットだから，各$n\in\N$に対して「$\lambda\succeq\lambda_n$かつ$\lambda'\succeq\lambda_n$を満たす任意の$\lambda,\lambda'\in\Lambda$に対して$d(x_\lambda,x_{\lambda'})<2^{-n}$が成り立つ」という性質を満たす$\lambda_n\in\Lambda$が取れる．そこで写像$\phi:\N\to\Lambda$を帰納的に
$$ \phi(n):=\begin{cases}\lambda_0&(n=0),\\\lambda_n\vee\phi(n-1)&(n\ge 1)\end{cases}$$
で定めれば，$\seq{x_{\phi(n)}}{n}$はコーシー列となるから，ある点$x\in X$に収束する．

$\seq{x_{\phi(n)}}{n}$がコーシー列であることの説明：各$\varepsilon\in(0,\infty)$に対して$2^{-N}<\varepsilon$を満たす$N\in\N$を取れば，$N$以上の任意の$m,n\in N$に対して$\lambda_N\preceq\phi(N)\preceq\phi(m)$かつ$\lambda_N\preceq\phi(N)\preceq\phi(n)$より$d(x_{\phi(m)},x_{\phi(n)})<2^{-N}<\varepsilon$が成り立つ．

このとき$\net{x_\lambda}{\lambda\in\Lambda}$も$x$に収束することを示すため，$\varepsilon\in(0,\infty)$を任意に取る．すると次の2性質を満たす$N_1,N_2\in\N$が取れる：

$2^{-N_1}<\varepsilon/2$である．
$N_2$以上の任意の$n\in\N$に対して$d(x_{\phi(n)},x)<\varepsilon/2$が成り立つ．

そこで$N:=\max(\{N_1,N_2\})$とおけば，$\lambda\succeq\phi(N)$を満たす任意の$\lambda\in\Lambda$に対して
$$ d(x_\lambda,x)\le d(x_\lambda,x_{\phi(N)})+d(x_{\phi(N)},x)<2^{-N}+\frac{\varepsilon}{2}<\varepsilon$$が成り立つから，$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に収束する．

連続写像とネット

距離空間における連続写像（復習）

距離空間$\pair{X,d_X},\pair{Y,d_Y}$と写像$f:X\to Y$および点$x\in X$に対して，$f$が$x$において連続であるとは，各$\varepsilon\in(0,\infty)$に対して「$d_X(x',x)<\delta$を満たす任意の$x'\in X$に対して$d_Y(f(x'),f(x))<\varepsilon$が成り立つ」という性質を満たす$\delta\in(0,\infty)$が存在することをいう．

ネットの収束による連続性の特徴づけ

距離空間$\pair{X,d_X},\pair{Y,d_Y}$と写像$f:X\to Y$および点$x\in X$に対して，次の2条件は同値である．

$f$は$x$において連続である．
任意の有向集合$\pair{\Lambda,\preceq}$と$x$に収束する$X$上の任意のネット$\net{x_\lambda}{\lambda\in\Lambda}$に対して，$\net{f(x_\lambda)}{\lambda\in\Lambda}$は$f(x)$に収束する．

$(1)\Rightarrow(2)$：詳細
有向集合$\pair{\Lambda,\preceq}$と$x$に収束する$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$および$\varepsilon\in(0,\infty)$を任意に取る．このとき$f$の$x$における連続性より「$d_X(x',x)<\delta$を満たす任意の$x'\in X$に対して$f_Y(f(x'),f(x))<\varepsilon$が成り立つ」という性質を満たす$\delta\in(0,\infty)$が取れて，$\net{x_\lambda}{\lambda\in\Lambda}$が$x$に収束することから「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)<\delta$が成り立つ」という性質を満たす$\lambda\in\Lambda$が取れる．このとき$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)<\delta$より$f_Y(f(x_\lambda),f(x))<\varepsilon$が成り立つから，$\net{f(x_\lambda)}{\lambda\in\Lambda}$は$f(x)$に収束する．
$(2)\Rightarrow(1)$：詳細
$\varepsilon\in(0,\infty)$を任意に取る．もし$f$が$x$において連続でなければ，各$\delta\in(0,\infty)$に対して$d_X(x_\delta,x)<\delta$かつ$d_Y(f(x_\delta),f(x))\ge\varepsilon$を満たす$x_\delta\in X$を取ることによって$X$上のネット$\net{x_\delta}{\delta\in(0,\infty)}$が得られる（$(0,\infty)$は逆大小関係によって有向集合とみなす）．このとき
$$ \limsup_{\delta\in(0,\infty)}d_X(x_\delta,x)\le\limsup_{\delta\in(0,\infty)}\delta=0$$
より$\net{x_\delta}{\delta\in(0,\infty)}$は$x$に収束するが，一方
$$ \limsup_{\delta\in(0,\infty)}d_Y(f(x_\delta),f(x))\ge\varepsilon>0$$
より$\net{f(x_\delta)}{\delta\in(0,\infty)}$は$f(x)$に収束しないので(2)に矛盾する．したがって$f$は$x$において連続である．

ネットの収束による一様連続性の特徴づけ

距離空間$\pair{X,d_X},\pair{Y,d_Y}$と写像$f:X\to Y$に対して，次の2条件は同値である．

$f$は一様連続である．
「$\net{d_X(x_\lambda,x_\lambda')}{\lambda\in\Lambda}$が$0$に収束する」という性質を満たす任意の有向集合$\pair{\Lambda,\preceq}$と$X$上の任意のネット$\net{x_\lambda}{\lambda\in\Lambda},\net{x_\lambda'}{\lambda\in\Lambda}$に対して，$\net{d_Y(f(x_\lambda),f(x_\lambda'))}{\lambda\in\Lambda}$は$0$に収束する．

$(1)\Rightarrow(2)$：詳細
有向集合$\pair{\Lambda,\preceq}$と
$$ \limsup_{\lambda\in\Lambda}d_X(x_\lambda,x_\lambda')\le 0$$
を満たす$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda},\net{x_\lambda'}{\lambda\in\Lambda}$を任意に取る．写像$\omega_f:[0,\infty]\to[0,\infty]$を次式で定めると，$f$の一様連続性より$\omega_f$は$0$において連続である．
$$ \omega_{f}(\delta):=\sup\{d_Y(f(x),f(x'))\mid x,x'\in X,\ d_X(x,x')\le\delta\} \qquad (\delta\in[0,\infty]).$$
また仮定より$\net{d_X(x_\lambda,x_\lambda')}{\lambda\in\Lambda}$は$0$に収束するため，$\net{\omega_f(d_X(x_\lambda,x_\lambda'))}{\lambda\in\Lambda}$は$\omega_f(0)=0$に収束する．すると，任意の$\lambda\in\Lambda$に対して$d_Y(f(x_\lambda),f(x_\lambda'))\le\omega_f(d_X(x_\lambda,x_\lambda'))$が成り立つことから
$$ \limsup_{\lambda\in\Lambda}d_Y(f(x_\lambda),f(x_\lambda'))\le \limsup_{\lambda\in\Lambda}\omega_f(d_X(x_\lambda,x_\lambda'))\le 0.$$
$(2)\Rightarrow(1)$：詳細
$\varepsilon\in(0,\infty)$を任意に取る．もし$f$が一様連続でなければ，各$\delta\in(0,\infty)$に対して$d_X(x_\delta,x_\delta')<\delta$かつ$d_Y(f(x_\delta),f(x_\delta'))\ge\varepsilon$を満たす$x_\delta,x_\delta'\in X$を取ることによって$X$上のネット$\net{x_\delta}{\delta\in(0,\infty)},\net{x_\delta'}{\delta\in(0,\infty)}$が得られる（$(0,\infty)$は逆大小関係によって有向集合とみなす）．このとき
$$ \limsup_{\delta\in(0,\infty)}d_X(x_\delta,x_\delta')\le\limsup_{\delta\in(0,\infty)}\delta=0$$
より$\net{d_X(x_\delta,x_\delta')}{\delta\in(0,\infty)}$は$0$に収束するが，一方
$$ \limsup_{\delta\in(0,\infty)}d_Y(f(x_\delta),f(x_\delta'))\ge\varepsilon>0$$
より$\net{d_Y(f(x_\delta),f(x_\delta'))}{\delta\in(0,\infty)}$は$0$に収束しないから(2)に矛盾する．したがって$f$は一様連続である．

一様連続写像はコーシーネットをコーシーネットにうつす

$\pair{\Lambda,\preceq}$を有向集合，$\pair{X,d_X},\pair{Y,d_Y}$を距離空間とし，$f:X\to Y$を一様連続写像，$\net{x_\lambda}{\lambda\in\Lambda}$を$X$上のコーシーネットとする．このとき，$\net{f(x_\lambda)}{\lambda\in\Lambda}$もコーシーネットである．

写像$\omega_f:[0,\infty]\to[0,\infty]$を次式で定めると，$f$の一様連続性より$\omega_f$は$0$において連続である．
$$ \omega_{f}(\delta):=\sup\{d_Y(f(x),f(x'))\mid x,x'\in X,\ d_X(x,x')\le\delta\} \qquad (\delta\in[0,\infty]).$$
また$\net{x_\lambda}{\lambda\in\Lambda}$がコーシーネットであることから$\net{d_X(x_\lambda,x_\mu)}{\pair{\lambda,\mu}\in\Lambda\times\Lambda}$は$0$に収束するため，$\net{\omega_f(d_X(x_\lambda,x_\mu))}{\pair{\lambda,\mu}\in\Lambda\times\Lambda}$は$\omega_f(0)=0$に収束する．すると，任意の$\pair{\lambda,\mu}\in\Lambda\times\Lambda$に対して$d_Y(f(x_\lambda),f(x_\mu))\le\omega_f(d_X(x_\lambda,x_\mu))$が成り立つことから
$$ \limsup_{\pair{\lambda,\mu}\in\Lambda\times\Lambda}d_Y(f(x_\lambda),f(x_\mu))\le \limsup_{\pair{\lambda,\mu}\in\Lambda\times\Lambda}\omega_f(d_X(x_\lambda,x_\mu))\le 0.$$

余談：位相空間におけるネット

ネットの収束

位相空間上のネットに対しても，収束を次のように定義することができる．

位相空間におけるネットの収束

$\pair{\Lambda,\preceq}$を有向集合，$\pair{X,\mathcal{O}}$を位相空間とする．このとき$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$が点$x\in X$に収束するとは，$x$の各近傍$N$に対して「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$x_\mu\in N$が成り立つ」という性質を満たす$\lambda\in\Lambda$が存在することをいう．

距離空間上のネットに対しては2通りの方法で収束を定義したが，これらの定義は同値である．

$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に（定義1の意味で）収束する．
$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に（定義5の意味で）収束する．ただし，$X$は$d$が定める距離位相によって位相空間とみなす．

$(1)\Rightarrow(2)$：詳細
$x$の近傍$N$を任意に取る．このとき$B(x,\varepsilon):=\{y\in X\mid d(y,x)<\varepsilon\}\subset N$を満たす$\varepsilon\in(0,\infty)$が取れるから，(1)より「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$d(x_\mu,x)< \varepsilon$が成り立つ」という性質を満たす$\lambda\in\Lambda$が存在する．このとき$\varepsilon$の取り方によって，$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$x_\mu\in B(x,\varepsilon)\subset N$が成り立つから，$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に(2)の意味でも収束する．
$(2)\Rightarrow(1)$：詳細
$\varepsilon\in(0,\infty)$を任意に取る．このとき$B(x,\varepsilon)$は$x$の近傍だから，(2)より「$\mu\succeq\lambda$を満たす任意の$\mu\in\Lambda$に対して$x_\mu\in B(x,\varepsilon)$が成り立つ」という性質を満たす$\lambda\in\Lambda$が取れる．したがって，$\net{x_\lambda}{\lambda\in\Lambda}$は$x$に(1)の意味でも収束する．

収束$\Rightarrow$部分ネットも収束

$\pair{\Lambda,\preceq_\Lambda},\pair{M,\preceq_M}$を有向集合，$\pair{X,\mathcal{O}}$を位相空間とし，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$と点$x\in X$を考える．
このとき$\net{x_\lambda}{\lambda\in\Lambda}$が$x$に収束するならば，$\net{x_\lambda}{\lambda\in\Lambda}$の任意の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$も$x$に収束する．

$x$の近傍$N$を任意に取る．このとき$\net{x_\lambda}{\lambda\in\Lambda}$が$x$に収束することから「$\lambda\succeq_\Lambda\lambda_0$を満たす任意の$\lambda\in\Lambda$に対して$x_\lambda\in N$が成り立つ」という性質を満たす$\lambda_0\in\Lambda$が取れて，部分ネットの定義から「$\mu\succeq_M\mu_0$を満たす任意の$\mu\in M$に対して$\lambda_0\preceq_\Lambda\phi(\mu)$が成り立つ」という性質を満たす$\mu_0\in M$が取れる．すると$\mu\succeq_M\mu_0$を満たす任意の$\mu\in M$に対して，$\lambda_0\preceq_\Lambda\phi(\mu)$より$x_{\phi(\mu)}\in N$が成り立つから，$\net{x_{\phi(\mu)}}{\mu\in M}$も$x$に収束する．

距離空間とは違い，ハウスドルフでない位相空間においては極限の一意性は成り立たない．

コンパクト性

位相空間における様々な概念をネットの収束によって書き直せることが知られているが，ここではコンパクト性について軽く触れるに留める．

コンパクト空間（復習）

位相空間$\pair{X,\mathcal{O}}$がコンパクトであるとは，$X$の任意の開被覆が有限部分被覆を持つことをいう．

収束部分ネットの存在

$\pair{\Lambda,\preceq}$を有向集合，$\pair{X,\mathcal{O}}$を位相空間とする．このとき，$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$と点$x\in X$が次の性質：

各$\lambda\in\Lambda$と$x$の各近傍$N$に対して，$\lambda_0\succeq\lambda$かつ$x_{\lambda_0}\in N$を満たす$\lambda_0\in\Lambda$が存在する．
（つまり，各$\lambda\in\Lambda$に対して$x\in\overline{\{x_{\lambda'}\mid \lambda'\in\Lambda,\ \lambda\preceq\lambda'\}}$が成り立つ．）

を満たすならば，$\net{x_\lambda}{\lambda\in\Lambda}$の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$であって$x$に収束するものが存在する．

$x$の近傍系$\mathcal{N}(x)$を逆包含関係によって有向集合とみなすと，$M:=\{\pair{\lambda,N}\in\Lambda\times\mathcal{N}(x)\mid x_\lambda\in N\}$は直積順序の制限によって有向集合となる．

$M$が有向集合となることの説明：詳細
$\pair{\lambda,N},\pair{\lambda',N'}\in M$を任意に取ると，まず$\{\lambda,\lambda'\}$の上界$\lambda''\in\Lambda$が存在する．すると仮定より$\lambda_0\succeq\lambda''$かつ$x_{\lambda_0}\in N\cap N'$を満たす$\lambda_0\in\Lambda$が取れるが，このとき$\pair{\lambda_0,N\cap N'}\in M$が$\{\pair{\lambda,N},\pair{\lambda',N'}\}$の上界となっている．

あとは，写像$\phi:M\ni\pair{\lambda,N}\mapsto \lambda\in\Lambda$が所望の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$を定めることを確かめればよい．

部分ネットであること：詳細
各$\lambda\in\Lambda$に対して$\mu:=\pair{\lambda,X}$とおくと，$\mu\preceq\nu$を満たす任意の$\nu\in M$に対して直積順序の定義から$\lambda\preceq\phi(\nu)$が成り立つ．
$x$に収束すること：詳細
$N\in\mathcal{N}(x)$を任意に取ると，仮定より$x_\lambda\in N$を満たす$\lambda\in\Lambda$が存在する．このとき$\pair{\lambda,N}\in M$であり，$\pair{\lambda',N'}\succeq\pair{\lambda,N}$を満たす任意の$\pair{\lambda',N'}\in M$に対して$x_{\phi(\lambda',N')}=x_{\lambda'}\in N'\subset N$が成り立つから，$\net{x_{\phi(\mu)}}{\mu\in M}$は$x$に収束する．

ネットの収束によるコンパクト性の特徴づけ

位相空間$\pair{X,\mathcal{O}}$について，次の2条件は同値である．

$\pair{X,\mathcal{O}}$はコンパクトである．
任意の有向集合$\pair{\Lambda,\preceq}$と$X$上の任意のネット$\net{x_\lambda}{\lambda\in\Lambda}$に対して，$\net{x_\lambda}{\lambda\in\Lambda}$の部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$と点$x\in X$で「$\net{x_{\phi(\mu)}}{\mu\in M}$は$x$に収束する」という性質を満たすものが存在する．

$(1)\Rightarrow(2)$：詳細
有向集合$\pair{\Lambda,\preceq}$と$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$を任意に取る．このとき各$\lambda\in\Lambda$に対して開集合$U_\lambda$を
$$ U_\lambda:=\{x_{\lambda'}\mid \lambda'\in\Lambda,\ \lambda\not\preceq\lambda'\}^\circ$$
で定めると，$\net{U_\lambda}{\lambda\in\Lambda}$は$X$を被覆しない．もし被覆すると仮定すると，(1)よりある有限個の添字$\lambda_1,\ldots,\lambda_n\in\Lambda$によって$X=U_{\lambda_1}\cup\cdots\cup U_{\lambda_n}$と書けるが，$\{\lambda_1,\ldots,\lambda_n\}$の上界$\lambda_{\ast}\in\Lambda$を取れば$X=U_{\lambda_{\ast}}\not\ni x_{\lambda_{\ast}}$となり矛盾するからである．したがってどの$U_\lambda$にも属さない点$x\in X$が存在し，前補題より$x$に収束する部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$も存在する．
$(2)\Rightarrow (1)$：詳細
$X$の開被覆$\mathcal{U}$を任意に取り，$\mathcal{U}$の有限部分集合全体の集合$\Lambda$を包含関係によって有向集合とみなす．もし$X$がコンパクトでなければ，各$\lambda\in\Lambda$に対して$x_\lambda\in X\setminus\bigcup\lambda$を満たす$x_\lambda\in X$を取ることによって$X$上のネット$\net{x_\lambda}{\lambda\in\Lambda}$が得られ，さらに(2)よりある部分ネット$\net{x_{\phi(\mu)}}{\mu\in M}$がある点$x\in X$に収束する．このとき$U\in\mathcal{U}$と$x$の近傍$N$を任意に取ると，次の2性質を満たす$\mu,\mu'\in M$が取れる．
- （部分ネットの定義）$\nu\succeq\mu$を満たす任意の$\nu\in M$に対して$\{U\}\subset\phi(\nu)$が成り立つ．
- （$\net{x_{\phi(\mu)}}{\mu\in M}$が$x$に収束する）$\nu\succeq\mu'$を満たす任意の$\nu\in M$に対して$x_{\phi(\nu)}\in N$が成り立つ．
そこで$\{\mu,\mu'\}$の上界$\mu''\in M$を取れば，$x_{\phi(\mu'')}\in N$であり，さらに$\net{x_\lambda}{\lambda\in\Lambda}$の取り方から
$$ x_{\phi(\mu'')}\in X\setminus\bigcup\phi(\mu'')\subset X\setminus\bigcup\{U\}=X\setminus U$$
も成り立つ．つまり$X\setminus U$は$x$の任意の近傍$N$と交わるから$x\in\overline{X\setminus U}=X\setminus U$であるが，$U$は任意だったから$\mathcal{U}$が$X$の開被覆であることに矛盾する．したがって，$X$はコンパクトである．