準同型をExcelのシートで説明してみる
準同型について
数学の特に代数学の概念で、準同型という概念がある。より強力な同型という概念を緩めた対応付けに「準じる」概念なので「準」がついている。
何かと何かが全く同じでなくてもほぼ同じと見なせることとそのの対応付けを「同型」、さらに緩めた同じと見なせるときのその対応付けを「準同型」という。
それが、$\mathbb{X}$で
話題になっていた
ので、考えたことをことを記事にした。
[Link]「
準同型 - Wikipedia
」
代数系
集合に、構造を入れたもの(集合と構造の組)を考える。特に代数学では二項演算を入れたものを考えて、それを「
代数系
」という。
2025/8/14 18:05 指摘を受けたので誤っていた部分を修正
集合とそこでの演算の規則の族の組を、「
代数系
」と呼ぶ。代数系の集合を台集合と呼ぶが、混乱の恐れがない場合にはそのまま台集合を代数系といって、同じ記号で表す。
代数系に関しては以下の記事にいくつかの定義や例を書いた
[Link]「
エックマン-ヒルトンの定理の視覚的証明が面白い | Mathlog
」
その特定の代数系と言えるものの実例が複数あったとして、複数の実例が注目している性質を満たすかどうかを判断する上では「同じである」ことを同型だといいたい。
写像
$2$つの集合(見かけ上$2$つ、$1$つでもよい)$X,Y$があるとき、$X$から$Y$への写像という、$X$の$1$つの要素$x$に対して、$Y$の$1$つの要素$y$を対応づける概念を考えられる。
$1$つの写像を$f$で表すとき、
$f:X \longrightarrow Y$
$x \longmapsto y$
$y=f(x)$
などと書く。
このとき、一方の要素$X$からもう一方の要素$y$へ「写る」ともいう。写り元全体を定義域(または始域)、写り先全体を終域という
例えば、$n$を$1$つの整数とするとき、$2n$を対応させる、つまり$2$倍する対応付けは、整数から整数への写像である。そのまま、整数から偶数への写像ともみなせる。$n$に対して、$n^2$を対応させるのもまた別の写像である。
単射と全射(この記事では、やや脱線なので読み飛ばしてOK)
写像の性質として、単射と全射というのがある。
異なる要素が、同じ要素に写らない写像を単射であるという。例えば、
$n \longmapsto 2n $は単射である。
$n \longmapsto n^2$は単射でない。(∵$2$も$-2$も4に写るから)
写り先の要素のすべてに、その写像での写り元がある写像を全射という。
写り元全体を整数全体、写り先全体を整数全体とすると、
$n \longmapsto 2n $について、奇数には写るものはないから、全射ではない。しかし、写り先全体を偶数全体とすると、どの偶数$m(=2n)$にも移り元$\frac{m}{2}(=n)$があるので全射である。
整数全体から整数全体の写像
$n \longmapsto n^2$は全射ではない(∵非負整数や$2$や$3$へ写る要素が無い)
例えば、単射と全射の両方を満たす写像を全単射という。
整数全体から整数全体の写像
$n \longmapsto n+1$は全単射である。
単射と全射に関することは別の記事に書いた
「
集合論の単射と全射に関する練習問題 | Mathlog
」
代数系の準同型とは
代数系の写像が、「演算を保つ」とき写像は準同型写像であるという。略して「準同型」ともいう。
写像が準同型でかつ、全単射とのとき、同型写像(略して同型)という。また、同型写像があるとき、始域の代数系と終域の代数系は「同型」であるという。
準同型、演算を保つとは
$ \circ $:$X$の演算
$ \bullet $:$Y$の演算
$f:X \longrightarrow Y$
として、
$\forall x,x' \in X; f(x \circ x')=f(x) \bullet f(x')$
が成り立つとき、準同型という。「演算を保つ」ともいう。
$2$つの要素を演算した後に写像で写すのと、それぞれ同じ写像で写した要素を演算するのと結果が同じときである。
例えば、整数のたし算を演算として、整数全体から整数全体の写像
$f:n \longmapsto 2n $は準同型である。
∵$n,m \in \mathbb{Z} ;f(n+m)=2(n+m)=2n+2m=f(n)+f(m)$∎
整数のたし算を演算として、整数全体から整数全体の写像
$g:n \longmapsto n^2 $は準同型ではない。
∵
$ g(1+2)=3^2=9$
$ g(1)+g(2)=1+4=5 \neq 9$∎
準同型をより簡単な例で説明してみる
この記事の本題はここからである。
準同型(写像)の例を日常の言葉やExcelシートを使って説明を試みる。
文字列とその連結
異なる種類の文字が連なったものを文字列という。
$2$つの文字列をつなげることを連結という。例えば、
「I have a pen.」と
「I have an apple.」とを「連結」すると
「I have a pen.I have an apple.」になる。
Excelシートの数式では、文字列の連結は「&」で行う。
 文字列の連結
文字列の連結
文字列全体の集合を考えると、「連結」は二項演算と見なせる。
- 文字列の連結結果は文字列になる。
- $3$つの文字列について、最初の$2$つを連結したものと最後との連結、最初と、残り$2$つを連結したものを連結した文字列は等しい。
- 文字が$1$つもないものも特別な「文字列」と見なし「空文字列」という。他の文字列と連結してもその文字列と同じものになる。
一般に集合$M$とその演算$\circ $が以下の条件で代数系をなすとき、
- $\forall s,t \in M;s\circ t \in M $
- $\forall s,t,u \in M;(s\circ t)\circ u=s\circ (t\circ u)$
- $\exists e \in M;\forall s \in M;s\circ e=e \circ s=s$
その代数系を
モノイド
と呼ぶ。この$e$を単位元と呼ぶ。
すなわち、文字列全体集合は「連結」を演算、「空文字列」を「単位元」としてモノイドである。
ついでにいうと、関係式(単位元と等しい非自明な複数の要素の演算結果)を何も仮定しない場合は「自由」と呼ばれるので、自由モノイドである。
モノイドの定義や関連する興味深い事実を別の記事
「
エックマン-ヒルトンの定理の視覚的証明が面白い | Mathlog
」
にも書いた。
Excelの文字列関数
Excelの数式には、与えられた文字列の中の英字小文字をすべて大文字にする関数「UPPER 関数」
[Link]「
UPPER 関数 - Microsoft サポート
」
がある。
これは文字列の集合から文字列の集合への写像とみなせる。
これを「大文字化」と呼ぶことにする。
この写像は例えば、
「I hava a pen.」を
「I HAVA A PEN.」に写す。
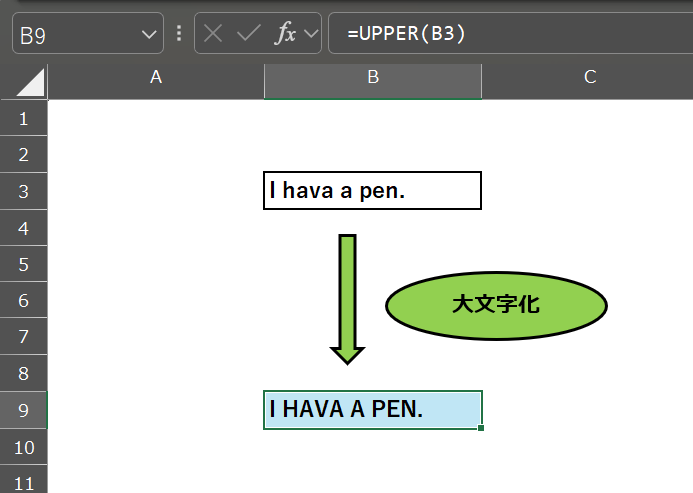 文字列の大文字化
文字列の大文字化
ちなみに、終域を「文字列の集合全体」としたとき、この写像は単射でも全射でもない。
大文字化の写像は準同型(連結演算を保つ)
結論から言うと、この写像(UPPER 関数)は、文字列の連結演算を保つので「準同型(写像)」である。
このことをExcelシートでExcelの数式とセル参照を利用して表す。
左上の$2$つのセル(B3,C3)を文字列の入力セルとする。
- 入力セルの下方(左下)にあるセル(B9,C9)に大文字化の結果のセルを配置する。
B9には「=UPPER(B3)」と入力。
C9には「=UPPER(C3)」と入力。 - 入力セルの右方(右上)にあるセル(G3)に、入力セルの$2$つの文字列を連結した結果のセルを配置する。
G3には「=B3&C3」と入力。 - 大文字化した$2$つのセルの参照して連結するセルを配置する。F9に「=B9&C9」と入力。
- 連結結果のセルを参照して大文字化するセルを配置する。
G8に「=UPPER(G3)」と入力。 - G9に一致を確認するセルを配置する。
G9に「=F9=G8」
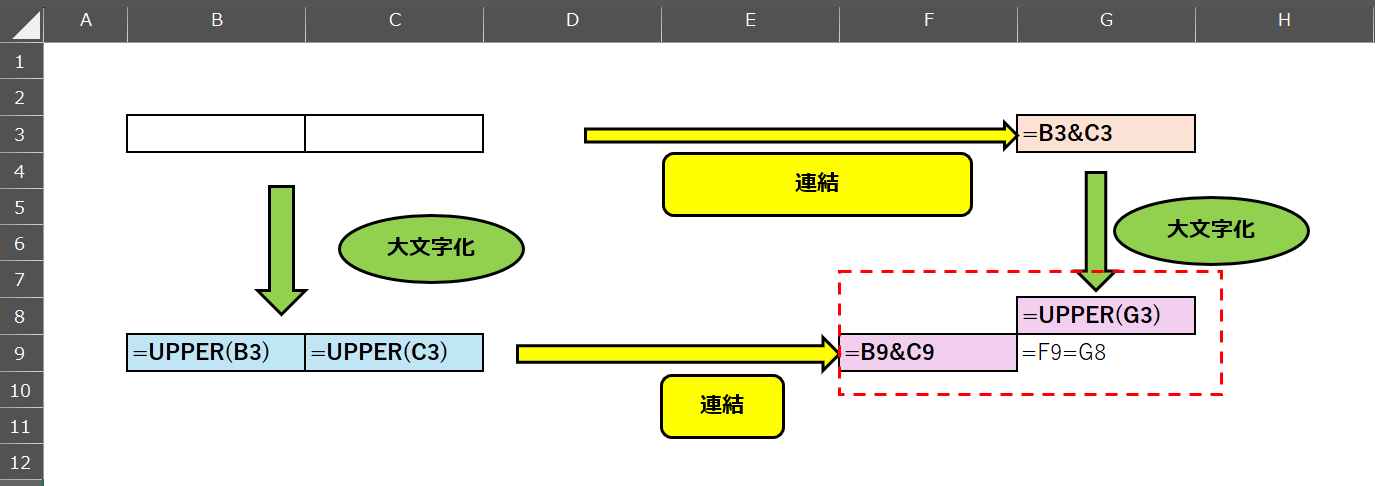 文字列の連結と大文字化
文字列の連結と大文字化
Excelシートのセルの数式入力した数式を確認したいときは、
ショートカットキーで、[Ctrl]+[Shift]+[@]
元に戻すのも、同じキーで行う。
そして、実際に左上の入力セル$2$つに文字列を入力すると右下の$2$つのセルは同じ値になるのが確認できる。
「連結してから大文字化」と「大文字化してから連結」との結果が一致する。「大文字化の写像は連結の演算を保つ」ので、大文字化の写像(UPPER 関数)は「準同型」である。
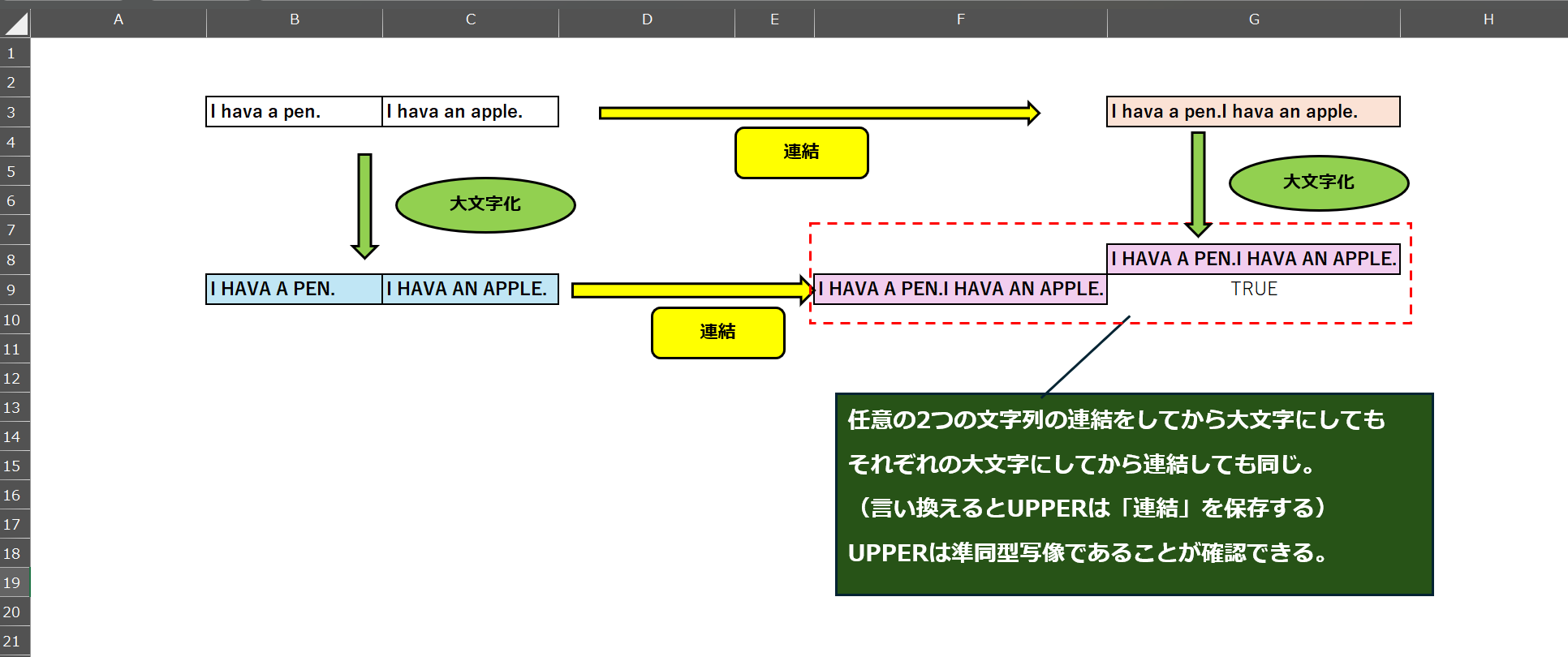 文字列の連結と大文字化の実例
文字列の連結と大文字化の実例
文字列の長さの写像も準同型である
別の例として、終域が非負整数全体(ここでは物理的な上限は考えない)となる、与えられた文字列の長さを返す「LEN 関数」
[Link]「
LEN 関数 - Microsoft サポート
」 がある。
これは、文字列全体から非負整数全体への写像である。
ただし、終域の演算は数値の和$+$となる。
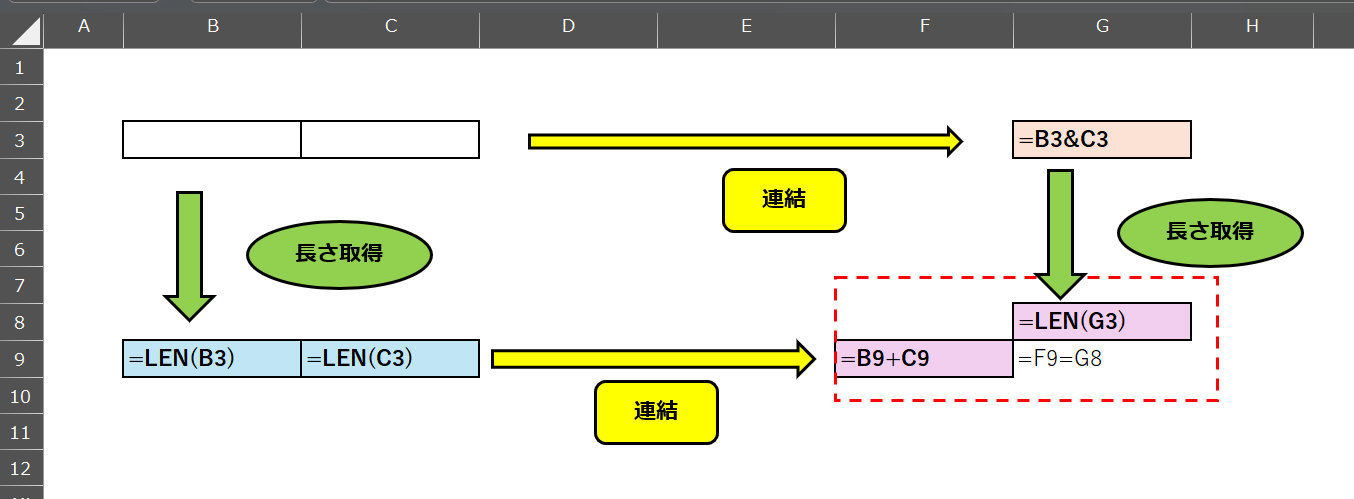 連結と文字列の長さ
連結と文字列の長さ
この写像も「準同型」となる。
どのような$2$つの文字列でも、連結してから長さを取得しても、まず長さを取得して、その和を計算しても、同じ値になるからである。
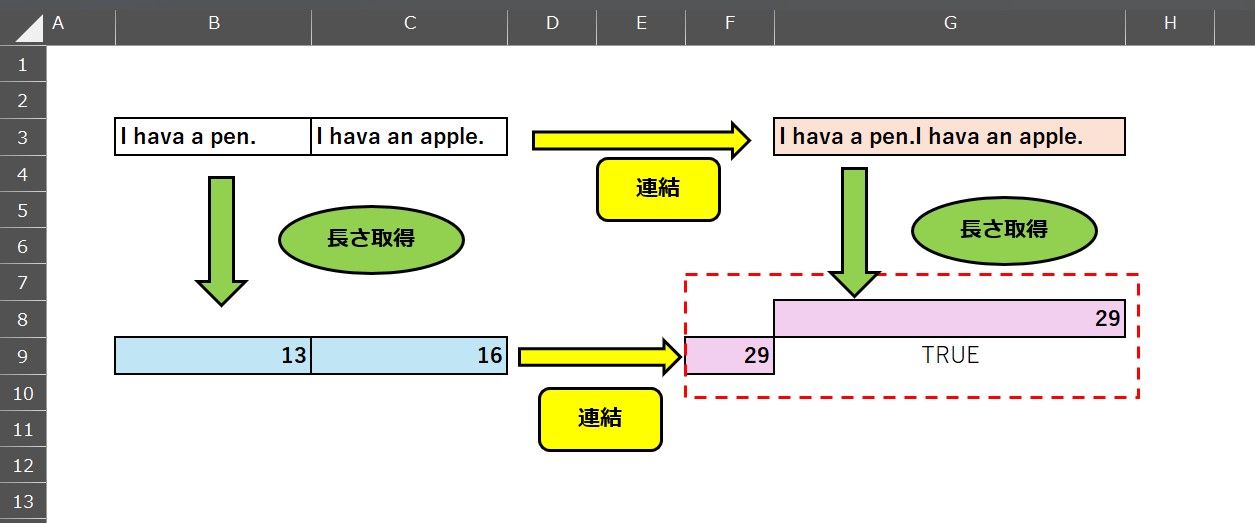 連結と文字列の長さの確認
連結と文字列の長さの確認
終わりに
演算や写像の処理を異なる$2$つの順番で行っても同じ結果になるような図式は、代数学や圏論など高度な数学で、「 可換図式 - Wikipedia」 と呼ばれる。準同型はその簡単な例にもなっている。
「準同型」についてはどういうものかは理解されている方も多いと思うが、周りの「準同型」についてまだ未知であると考えてる人に、説明しようと思うとなかなかうまく説明できないかもしれない。この説明や例でも必ずしも周りの人が理解できるとも限らないが、日常の言葉での説明できる実例の案を思いついたのでこの記事を書いた。もちろんより良い説明を発見できるかもしれない、その「発見」のきっかけになることを期待する。