応用数学解説

文献あり

八元数による7次元回転

八元数,回転

342

八元数の基本性質と7次元回転について説明します。

八元数についての基本事項は記事内で説明するため、前提とはしません。また、必ずしも四元数を前提とはしませんが、その延長線上で扱うため、四元数の知識があればスムーズです。

八元数の基本構造

八元数は、四元数を拡張した8次元の代数系です。実数、複素数、四元数に続くノルム付き可除代数として知られます。wiki-norm

八元数は以下のような特徴を持ちます：

8次元の数体系
非交換的（交換法則が成り立たない）
非結合的（結合法則が成り立たない）
ノルムを持つ（ノルムの積の法則が成立）

八元数は以下の8つの基底から構成されます：

八元数の基底

${1, e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}}$

ここで、1は実部を表し、 $e_{1}$ から $e_{7}$ は7つの虚数単位を表します。

実部の基底

$1$ ではなく $e_{0}$ と表記することもあります。この記事では、実部は基底を付けない実数として表記します。

八元数 $o$ は一般に以下の形で表されます：

$o = o_{0} + o_{1} e_{1} + o_{2} e_{2} + o_{3} e_{3} + o_{4} e_{4} + o_{5} e_{5} + o_{6} e_{6} + o_{7} e_{7}$

ここで、 $o_{0}, o_{1}, \dots, o_{7}$ は実数であり、 $e_{1}, e_{2}, \dots, e_{7}$ は虚数単位です。

虚数単位の性質

これらの虚数単位は以下の性質を持ちます：

各虚数単位の2乗は $- 1$ となる
$e_{i}^{2} = - 1$ （ $i = 1, 2, \dots, 7$ ）
積の順序を変えると符号が反転する（反交換性）
$e_{i} e_{j} = - e_{j} e_{i}$ （ $i \neq j$ ）
異なる虚数単位の積は別の虚数単位となり、組み合わせによっては負となる（反交換性を反映）
$e_{i} e_{j} = e_{k}$ または $- e_{k}$ （ $i, j, k$ は相異なる）

これらの性質により、八元数の乗法構造は複雑になりますが、同時に豊かな代数的・幾何学的構造を持つことになります。

八元数の共役は、虚部を符号反転として定義されます。この記事では上付きの $*$ で共役を表記します。

八元数とその共役

$\begin{aligned} o & = o_{0} + o_{1} e_{1} + o_{2} e_{2} + o_{3} e_{3} + o_{4} e_{4} + o_{5} e_{5} + o_{6} e_{6} + o_{7} e_{7} \\ o^{*} & = o_{0} - o_{1} e_{1} - o_{2} e_{2} - o_{3} e_{3} - o_{4} e_{4} - o_{5} e_{5} - o_{6} e_{6} - o_{7} e_{7} \end{aligned}$

八元数のノルムは以下のように定義されます：

八元数のノルム

$| o |^{2} = o o^{*} = o_{0}^{2} + o_{1}^{2} + o_{2}^{2} + o_{3}^{2} + o_{4}^{2} + o_{5}^{2} + o_{6}^{2} + o_{7}^{2}$

このノルムは、八元数の幾何学的な長さを表すと同時に、代数的な性質も持っています。特に、ノルムの積の法則が成立します：

ノルムの乗法性

$| o p | = | o | | p |$

ここで $o$ と $p$ は任意の八元数です。

八元数の乗法構造とファノ平面

八元数の乗法構造を理解するために、7つの三つ組（triads）を導入します。これらの三つ組は、互いに直交する3つの虚数単位から成り、四元数と同型な部分構造を形成します。

7つの三つ組の古典的な定義は以下の通りです：

グレイブスとケイリーによる三つ組

$(e_{1}, e_{2}, e_{3})$
$(e_{1}, e_{4}, e_{5})$
$(e_{1}, e_{7}, e_{6})$
$(e_{2}, e_{4}, e_{6})$
$(e_{2}, e_{5}, e_{7})$
$(e_{3}, e_{4}, e_{7})$
$(e_{3}, e_{6}, e_{5})$

1つの虚数単位は3つの三つ組に含まれます。各三つ組内では、四元数と同じ乗算規則が成り立ちます（例として最初の三つ組を使用）：

$\begin{aligned} e_{1} e_{2} & = - e_{2} e_{1} = e_{3} \\ e_{2} e_{3} & = - e_{3} e_{2} = e_{1} \\ e_{3} e_{1} & = - e_{1} e_{3} = e_{2} \end{aligned}$

三つ組の定義は一意には定まらず、480種類のバリエーションがあります。どれに基づいても八元数の代数的な性質は同じであるため、今回の記事では最初に発見されたグレイブス（1843）とケイリー（1845）による定義を使用します。7shi-480

ファノ平面による乗法規則の視覚化

八元数の乗法構造は、ファノ平面と呼ばれる幾何学的図形を用いて視覚化できます。ファノ平面は、7つの点と7つの線（うち1つは円）から成る射影平面です。

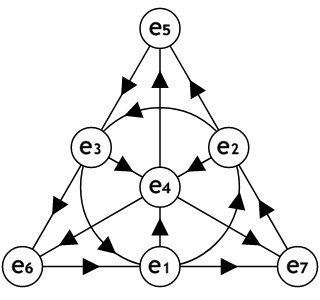ファノ平面

この図では、向き付けられた円と6本の線（三角形の3辺と3本の垂線）が、7つの三つ組に対応しています。円上に $e_{1}, e_{2}, e_{3}$ を配置し、それらと円の中心に置かれた $e_{4}$ との添え字の足し算によって、 $e_{5}, e_{6}, e_{7}$ が生成されるように配置しています。円と三角形上の線の向きは反時計回りで統一しています。

ファノ平面を用いて、八元数の乗法規則を以下のように構成できます：

線分は両端がつながっていると見なす。
（円が基本で、線分も円と同じ構造を持つが、図形上の都合で線分としている）
線（円を含む）上の2つの虚数単位の積は、矢印の順方向に隣接する場合は正、逆方向の場合は負の符号を伴った、残りの虚数単位となる。
（任意の2つの虚数単位を含む線が存在し、残りの1つは一意に決まる）

例えば：

$e_{1} e_{2} = e_{3}$ （ $e_{1}, e_{2}$ は円上で順方向に隣接）
$e_{2} e_{1} = - e_{3}$ （ $e_{2}, e_{1}$ は円上で逆方向に隣接）
$e_{1} e_{4} = e_{5}$ （ $e_{1}, e_{4}$ は線上で順方向に隣接）

このように、八元数の複雑な乗法構造を視覚的に理解することができます。実用上は、まずファノ平面を描いて、そこから三つ組が再構成できれば十分です。

ファノ平面のバリエーション

ファノ平面は虚数単位の置き方や線の向きにバリエーションがあります。三つ組の選択にも依存するため、他の資料に掲載されているファノ平面は必ずしも同じではありません。その場合でも、ファノ平面からの乗法規則の構成方法は同じです。

非結合性

八元数の重要な特徴の一つに非結合性があります。これは、3つ以上の八元数の積を計算する際に、括弧の位置によって結果が変わることを意味します。

非結合的な組み合わせ

$(e_{1} e_{2}) e_{4} \neq e_{1} (e_{2} e_{4})$

具体的に計算してみると：

$(e_{1} e_{2}) e_{4} = e_{3} e_{4} = e_{7}$
$e_{1} (e_{2} e_{4}) = e_{1} e_{6} = - e_{7}$

この例では結果が異なりましたが、一致する場合もあります：

結合的な組み合わせ

$(e_{1} e_{2}) e_{3} = e_{1} (e_{2} e_{3})$

$(e_{1} e_{2}) e_{3} = e_{3} e_{3} = - 1$
$e_{1} (e_{2} e_{3}) = e_{1} e_{1} = - 1$

組み合わせが1つの三つ組内で閉じている場合、結合的となります。これは四元数が結合的であることに対応します。

このように、八元数の乗法では必ずしも結合法則が成り立ちません。これは四元数までには見られなかった性質で、八元数の複雑さを示す特徴の一つです。非結合性があるため、八元数の計算では括弧の位置に注意を払う必要があります。

行列表現

結合的な代数系は行列で表現できますが、非結合的な系は行列で表現することは困難です。ただし制限付きでの行列表現は考えられており、別の記事で説明する予定です。

純虚八元数の積と7次元空間

純虚八元数は、実部がなく、虚部のみによって構成される八元数です。一般的な形式は以下のようになります：

純虚八元数

$x = x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3} + x_{4} e_{4} + x_{5} e_{5} + x_{6} e_{6} + x_{7} e_{7}$

純虚八元数は、7次元ベクトル空間の元に対応します：

$\vec{x} = (x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7})^{T}$

この対応により、純虚八元数の代数的操作を7次元空間の幾何学的操作として解釈することができます。

純虚八元数の積

純虚八元数 $v, w$ の積を計算します。

$\begin{aligned} v & = v_{1} e_{1} + v_{2} e_{2} + v_{3} e_{3} + v_{4} e_{4} + v_{5} e_{5} + v_{6} e_{6} + v_{7} e_{7} \\ w & = w_{1} e_{1} + w_{2} e_{2} + w_{3} e_{3} + w_{4} e_{4} + w_{5} e_{5} + w_{6} e_{6} + w_{7} e_{7} \\ v w & = - (v_{1} w_{1} + v_{2} w_{2} + v_{3} w_{3} + v_{4} w_{4} + v_{5} w_{5} + v_{6} w_{6} + v_{7} w_{7}) \\ + {(v_{2} w_{3} - v_{3} w_{2}) + (v_{4} w_{5} - v_{5} w_{4}) + (v_{7} w_{6} - v_{6} w_{7})} e_{1} \\ + {(v_{3} w_{1} - v_{1} w_{3}) + (v_{4} w_{6} - v_{6} w_{4}) + (v_{5} w_{7} - v_{7} w_{5})} e_{2} \\ + {(v_{1} w_{2} - v_{2} w_{1}) + (v_{4} w_{7} - v_{7} w_{4}) + (v_{6} w_{5} - v_{5} w_{6})} e_{3} \\ + {(v_{5} w_{1} - v_{1} w_{5}) + (v_{6} w_{2} - v_{2} w_{6}) + (v_{7} w_{3} - v_{3} w_{7})} e_{4} \\ + {(v_{1} w_{4} - v_{4} w_{1}) + (v_{7} w_{2} - v_{2} w_{7}) + (v_{3} w_{6} - v_{6} w_{3})} e_{5} \\ + {(v_{1} w_{7} - v_{7} w_{1}) + (v_{2} w_{4} - v_{4} w_{2}) + (v_{5} w_{3} - v_{3} w_{5})} e_{6} \\ + {(v_{6} w_{1} - v_{1} w_{6}) + (v_{2} w_{5} - v_{5} w_{2}) + (v_{3} w_{4} - v_{4} w_{3})} e_{7} \end{aligned}$

純虚八元数の積の実部を内積の符号反転、虚部を外積と定義します。

純虚八元数の内積と外積

$\begin{aligned} v \cdot w := & - Re (v w) \\ v \times w := & Im (v w) \\ v w = & - v \cdot w + v \times w \end{aligned}$

虚部の取得

複素数の虚部を取得する $Im$ は虚数単位 $i$ を含みません。それに対し、八元数では虚数単位が複数ある関係上、 $Im$ は虚数単位を含みます。

例: $Im (1 + 2 e_{1} + 3 e_{2}) = 2 e_{1} + 3 e_{2}$

内積と外積の性質について見ていきます。

内積の定義と性質

7次元ベクトル $\vec{v}, \vec{w}$ の内積は以下のように定義されます：

7次元ベクトルの内積

$\vec{v} \cdot \vec{w} = v_{1} w_{1} + v_{2} w_{2} + v_{3} w_{3} + v_{4} w_{4} + v_{5} w_{5} + v_{6} w_{6} + v_{7} w_{7}$

この定義は純虚八元数の内積と一致し、以下の性質を持ちます：

対称性: $\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}$
線形性: $(a \vec{v} + b \vec{w}) \cdot \vec{u} = a (\vec{v} \cdot \vec{u}) + b (\vec{w} \cdot \vec{u})$
正定値性: $\vec{v} \cdot \vec{v} \geq 0$ , かつ $\vec{v} \cdot \vec{v} = 0 ⟺ \vec{v} = \vec{0}$

3次元空間の特殊性と外積

7次元外積は3次元外積から構成されるため、まず3次元外積について説明します。

3次元空間では、任意の平面に対して向きの違いを除いて一意に法線ベクトルが定まります。この特殊性が、3次元空間での外積（ベクトル積）の定義を可能にします。

3次元ベクトル $\vec{a} = (a_{1}, a_{2}, a_{3})^{T}$ と $\vec{b} = (b_{1}, b_{2}, b_{3})^{T}$ の外積は以下のように定義されます：

3次元ベクトルの外積

$\vec{a} \times \vec{b} = (\begin{matrix} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{matrix})$

外積は $\vec{a}$ と $\vec{b}$ の両方に垂直なベクトルを生成します。これは $\vec{a}$ と $\vec{b}$ が張る平行四辺形に対する法線ベクトルとなり、長さはその平行四辺形の面積となります。

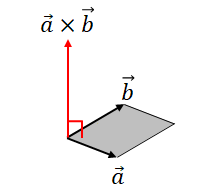外積（右手系）

法線ではなく、直接的に平面上の面積を扱う方法もあり、ウェッジ積と呼ばれます。ウェッジ積は3次元の特殊性には依存しません。7shi-oct

八元数による7次元外積の実現

7次元空間では平面に対する法線が定まらないため、外積を直接的には定義できません。

八元数は7つの三つ組を内包しています。これら三つ組は3次元部分空間を形成します。純虚八元数の積の虚部から定義される7次元外積は、各3次元部分空間内での外積を組み合わせた形となります：7shi-oct

7次元ベクトルの外積

$\vec{v} \times \vec{w} = (\begin{matrix} (v_{2} w_{3} - v_{3} w_{2}) + (v_{4} w_{5} - v_{5} w_{4}) + (v_{7} w_{6} - v_{6} w_{7}) \\ (v_{3} w_{1} - v_{1} w_{3}) + (v_{4} w_{6} - v_{6} w_{4}) + (v_{5} w_{7} - v_{7} w_{5}) \\ (v_{1} w_{2} - v_{2} w_{1}) + (v_{4} w_{7} - v_{7} w_{4}) + (v_{6} w_{5} - v_{5} w_{6}) \\ (v_{5} w_{1} - v_{1} w_{5}) + (v_{6} w_{2} - v_{2} w_{6}) + (v_{7} w_{3} - v_{3} w_{7}) \\ (v_{1} w_{4} - v_{4} w_{1}) + (v_{7} w_{2} - v_{2} w_{7}) + (v_{3} w_{6} - v_{6} w_{3}) \\ (v_{1} w_{7} - v_{7} w_{1}) + (v_{2} w_{4} - v_{4} w_{2}) + (v_{5} w_{3} - v_{3} w_{5}) \\ (v_{6} w_{1} - v_{1} w_{6}) + (v_{2} w_{5} - v_{5} w_{2}) + (v_{3} w_{4} - v_{4} w_{3}) \end{matrix})$

成分ごとに見ると、3つの3次元外積が組み合わされた形をしています。これは、1つの虚数単位が3つの三つ組に含まれる構造を反映しています。

八元数による7次元回転

一般に $n$ 次元空間における回転は、2次元部分空間を回転面として考えることができます。7shi-rot

7次元空間には以下の数の2次元部分空間の基底が存在します：

$(\binom{7}{2}) = 7 \times 6 \div 2 = 21$

したがって、7次元空間における一般的な回転は21個の独立したパラメーターによって完全に記述されます。これらのパラメーターによって、7次元空間内で任意の回転面が指定できます。

八元数による7次元回転は単位八元数によって指定されます。八元数は8つのパラメーターを持ちますが、単位八元数はノルムが $1$ という制約があるため自由度は7となります。そのため自由度が21である一般的な7次元回転を完全には表現できず、特定の種類の回転しか表現できません。nakajima

具体的には、回転軸に直交する3つの2次元平面で同期した回転となります。これは、7次元空間を3つの2次元平面と1つの1次元軸（回転軸）に分解していると解釈できます。

自由度

7次元回転の自由度21のうち、3つの平面で同時に回転することから自由度は21÷3=7となり、単位八元数の自由度7と一致します。

単位八元数による回転の表現

単位八元数 $r$ は以下の形式で表現できます：7shi-coord

単位八元数の指数関数表示

$\begin{aligned} r & = \exp (\frac{θ}{2} n) = \cos \frac{θ}{2} + \sin \frac{θ}{2} n \\ n & = n_{1} e_{1} + \dots + n_{7} e_{7} (n^{2} = - 1, n_{1}^{2} + \dots + n_{7}^{2} = 1) \end{aligned}$

ここで、 $θ$ は回転角、 $n$ は単位純虚八元数で回転軸を表します。

オイラーの公式

$n^{2} = - 1$ より $n$ は虚数単位と同一視できるため、 $r$ の定義ではオイラーの公式を適用しています。

具体的な回転操作は、単位八元数とその共役とで両側から挟むことで表現できます：

八元数による7次元回転

$(r x) r^{*} = r (x r^{*}) = (\cos \frac{θ}{2} + \sin \frac{θ}{2} n) x (\cos \frac{θ}{2} - \sin \frac{θ}{2} n)$

この操作は、 $n$ に直交する3つの2次元平面のそれぞれで $θ$ の回転を引き起こします。

交代代数

八元数が満たす交代代数の性質により $r x r^{*}$ は常に結合的です。wiki-alt

詳細はこちらの資料の1.19式を参照してください。nakajima

具体的な計算結果をベクトルとして示します：

$(\begin{matrix} \cos θ x_{1} + \sin θ {(n_{2} x_{3} - n_{3} x_{2}) + (n_{4} x_{5} - n_{5} x_{4}) + (n_{7} x_{6} - n_{6} x_{7})} + (1 - \cos θ) n_{1} (n \cdot x) \\ \cos θ x_{2} + \sin θ {(n_{3} x_{1} - n_{1} x_{3}) + (n_{4} x_{6} - n_{6} x_{4}) + (n_{5} x_{7} - n_{7} x_{5})} + (1 - \cos θ) n_{2} (n \cdot x) \\ \cos θ x_{3} + \sin θ {(n_{1} x_{2} - n_{2} x_{1}) + (n_{4} x_{7} - n_{7} x_{4}) + (n_{6} x_{5} - n_{5} x_{6})} + (1 - \cos θ) n_{3} (n \cdot x) \\ \cos θ x_{4} + \sin θ {(n_{5} x_{1} - n_{1} x_{5}) + (n_{6} x_{2} - n_{2} x_{6}) + (n_{7} x_{3} - n_{3} x_{7})} + (1 - \cos θ) n_{4} (n \cdot x) \\ \cos θ x_{5} + \sin θ {(n_{1} x_{4} - n_{4} x_{1}) + (n_{7} x_{2} - n_{2} x_{7}) + (n_{3} x_{6} - n_{6} x_{3})} + (1 - \cos θ) n_{5} (n \cdot x) \\ \cos θ x_{6} + \sin θ {(n_{1} x_{7} - n_{7} x_{1}) + (n_{2} x_{4} - n_{4} x_{2}) + (n_{5} x_{3} - n_{3} x_{5})} + (1 - \cos θ) n_{6} (n \cdot x) \\ \cos θ x_{7} + \sin θ {(n_{6} x_{1} - n_{1} x_{6}) + (n_{2} x_{5} - n_{5} x_{2}) + (n_{3} x_{4} - n_{4} x_{3})} + (1 - \cos θ) n_{7} (n \cdot x) \end{matrix})$

これをまとめると、八元数版のロドリゲスの回転公式が得られます：

八元数版ロドリゲスの回転公式

$\exp (\frac{θ}{2} n) x \exp (- \frac{θ}{2} n) = \cos θ x + \sin θ (n \times x) + (1 - \cos θ) n (n \cdot x)$

これは四元数による表式と同じ形をしています。7shi-rod

成分計算

成分計算はあまりに複雑なため、専用のプログラムを作成して計算しました。7shi-gist

その結果を手動で整理して示しました。

回転操作の幾何学的意味

回転操作 $r x r^{*}$ において、 $x$ の $n$ 方向の成分は変化しません。つまり、回転軸方向は保存されます。 $n$ に直交する空間は6次元で、これが3つの2次元平面に分解されます。各平面ではそれぞれ $θ$ 回転が起こります。

回転軸

n = e_{1}

の場合

$\begin{aligned} \exp (\frac{θ}{2} e_{1}) x \exp (- \frac{θ}{2} e_{1}) & = x_{1} e_{1} \\ + (\cos θ & x_{2} - \sin θ & x_{3}) e_{2} \\ + (\sin θ & x_{2} + \cos θ & x_{3}) e_{3} \\ + (\cos θ & x_{4} - \sin θ & x_{5}) e_{4} \\ + (\sin θ & x_{4} + \cos θ & x_{5}) e_{5} \\ + (\sin θ & x_{7} + \cos θ & x_{6}) e_{6} \\ + (\cos θ & x_{7} - \sin θ & x_{6}) e_{7} \end{aligned}$

$e_{1}$ の成分である $x_{1}$ が不変で、 $(e_{2}, e_{3}), (e_{4}, e_{5}), (e_{7}, e_{6})$ の3つの平面上で回転が起きています。この平面は $e_{1}$ を含む三つ組 $(e_{1}, e_{2}, e_{3}), (e_{1}, e_{4}, e_{5}), (e_{1}, e_{7}, e_{6})$ に由来します。

回転行列

個々の平面での回転は、2次元の回転行列に対応します。

$(\begin{matrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{matrix}) (\begin{matrix} x_{2} \\ x_{3} \end{matrix}) = (\begin{matrix} \cos θ x_{2} - \sin θ x_{3} \\ \sin θ x_{2} + \cos θ x_{3} \end{matrix})$