群の生成と準同型を一緒に学びたい記事
どうも
こんにちは ごててんです 暑い！！！ はやく夏を過ごし終わってブルーロックアニメ2期を見たいところです。
さて、この記事で扱う内容は「群の生成」と「群の準同型」になります。群論初心者向け記事です。部分群の定義と$\mathbb{Z}/n\mathbb{Z}$を知っていれば読めると思います！
群の生成とは？
数学をしていると、しばしば「生成」というものに出会います。この記事では「群」の生成を扱います。
部分群の例を見てみよう
群の例として$\mathbb{Z}$を考えてみます。整数全体の集合$\mathbb{Z}$は加法によって群になります。
さて、その部分集合を色々考えてみましょう。
$\{0\}$
これは$\mathbb{Z}$の部分群になります。単位元$0$があって、演算に閉じていて（$0+0=0$）、つねに逆元が取れます。（$0$の逆元は$0$）
$n\mathbb{Z}=\{nx | x\in\mathbb{Z}\}$
これも$\mathbb{Z}$の部分群になります。$0$は$n$の倍数。$n$の倍数同士の和も$n$の倍数。また$m$が$n$の倍数なら$-m$も$n$の倍数です。
$\mathbb{Z}$の部分群はすべて上の形で書けることが知られています。証明は...... なんか頑張ったらできます。
この記事で証明はしません。超ざっくりと証明の方針を書くと まず$H=\{0\}$の場合を除いて、部分群$H$に含まれる正の数でいちばん小さいものを取ってきて、すべての$H$の元がそれの整数倍で書けることを割り算とかを使って示します。群論に慣れてきたら、この証明くらいは何も見ずに書けると良いですね。
はい。ここまで、部分群となる例を見てきました。次は部分群とならない例です。
部分群にならない例を見てみよう
$\{2\}$
これは部分群になりませんね。いろいろダメです。たとえば、演算に閉じていません。（$2+2 \not \in \{2\}$）
$\{5,11\}$
これも部分群になりません。このように、群は考えなしに部分集合を取ってきても部分群にはなりません。
数学は執念深いので...
部分群にならない部分集合があったら何がしたいか。群論は群について考える学問なので、群になっていない集合を調べる理由などありません。ですが、部分群にならない部分集合に命を吹き込む方法があります。それが「部分群の生成」です。
部分群になっていない部分集合はどうして部分群になれていないのでしょうか。理由を次の3つに分けて考えてみます。
単位元がない
$\mathbb{Z}$の部分集合を考えてみても、そもそも$\{0\}$が含まれていなければどうしようもありません。
演算が閉じていない
群のいちばんの売りは演算です。その演算ができなければ意味がありませんね。
逆元が取れない
群のいちばんの売りは逆元です（爆速矛盾） 逆元が取れなければ意味がありませんね。
じゃあどうするのよ
みなさんお気づきでしょうか。上で挙げた3つの理由ですが、すべて一つの言葉でまとめることができます。それは「元が足りない！！！」というものです。
単位元がない
単位元がないというのは、「単位元が足りない」ということです。
演算が閉じていない
演算が閉じていないということは、$a,b$はあるのに$ab$が入っていないということで、「演算結果の$ab$が足りない」ということです。
逆元が取れない
逆元が取れないというのは、「逆元が足りない」ということです。
足りないのならどうすればいいでしょうか。足してあげればいいですね！！！！！
手探りで方法を考える
$\{2\}$ のケース
$S= \{2\}$とします。$S$は$\mathbb{Z}$の部分群になっていませんが、「もし$S=\{2\}$を含む部分群$H$があったら、どうなっているのだろう？」ということを考えてみます。
部分群は演算について閉じているので、たとえば$4=2+2 \in H$となっているはずです。また、$10\mathrm{億} = \underbrace{2+\dots +2}_{\text{2が超いっぱい}}$ なので、$10\mathrm{億} \in H$であるはずです。
部分群は逆元を取る操作について閉じているので、$-2 \in S$となっているはずです。ですので、$-2+2-2-2+2-2-2+2-2+2-2-2$ みたいに、$2$と$-2$を足しまくった数も$S$に含まれているはずです。
はい。というわけで、$S=\{2\}$を含む部分群$H$は、$2\mathbb{Z}=\{2x|x\in\mathbb{Z}\}$を含んでいそうです。実際含んでいます。
$\{5,11\}$ のケース
$S=\{5,11\}$とします。「もし$S=\{5,11\}$を含む部分群$H$があったら、どうなっているのだろう？」ということを考えてみます。
まあこちらは効率的に考えてしまいますか。$11-5-5=1 \in H$ということで$1$が作れます。
正の整数$a$を作りたい！となったら、$11-5-5$を$a$個つなげた式を作れば良いわけです。つまり、$H$は$\mathbb{Z}$の元をすべて作れますので、$H=\mathbb{Z}$となるしかありません。
アイキャッチ
この観察から
さて、$\{2\}$と$\{5,11\}$の$2$つの例を見てもらいました。ここから、部分群になっていない集合$S$について、$S$の元を足したり引いたりしまくったものを入れまくった集合を考えたら、部分群を作れるのでは？という発想が自然に沸き起こると思います。
ここで「$S$の元を足したり引いたりしまくったもの」をちゃんと定義しておきます。
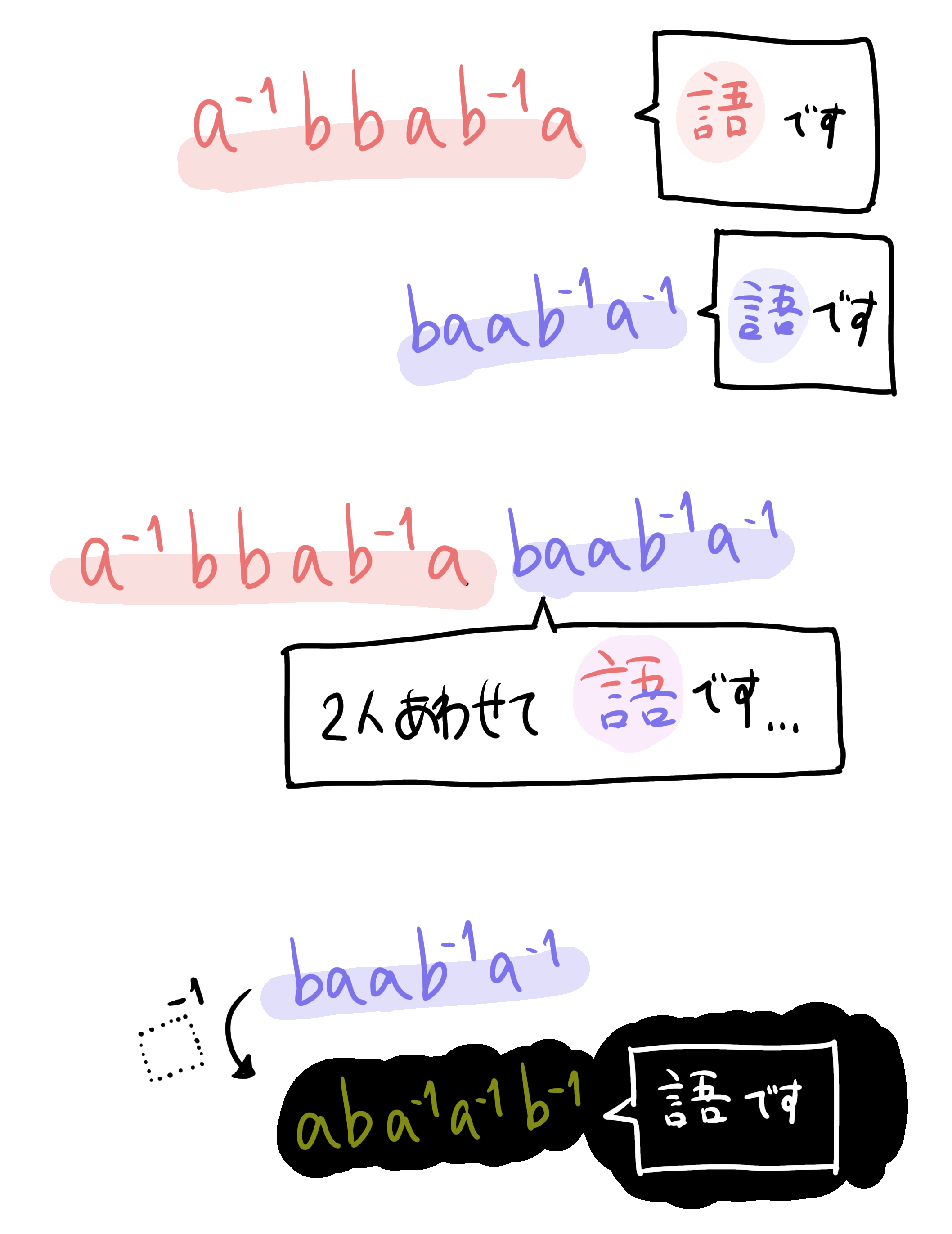
$G$を群, $S \subset G$を部分群とは限らない部分集合として, $T=\{x^{-1}|x \in S\}$, また$\Omega = S \cup T$とする. このとき、$x_1, \dots,x_n \in \Omega$によって $x_1 \dots x_n$という形をした元を$S$の元による語という.（また、$G$の単位元も$S$の元を$0$個つなげたものとみなし, 語に含めることにする）
群論の入門書などで、群の生成の定義でこの「語」を用いているケースはあまり無いと思います。初歩的な群論の話を同じ学年の人とかとするときにこの用語は使わないほうがいいと思います。
例を出しておきましょう。$\mathbb{C}\setminus\{0\}$の部分集合$S$を$S=\{2,\frac{4}{5},i\}$とすると、$\Omega=\{2,\frac{1}{2},\frac{4}{5},\frac{5}{4},i,-i\}$となっています。（$i$は虚数単位を表すとします）
このときの語は、例えば次のような感じです。
$2 \cdot (-i) \cdot \frac{5}{4} \cdot \frac{5}{4} \cdot \frac{4}{5} \cdot i \cdot 2$
$i\cdot i \cdot i$
$1$（$0$個つなげた場合）
$\frac{1}{2}$
$\frac{4}{5} \cdot 2 \cdot i$
他の例ですが、上の$S=\{2\}$としたときは$\Omega=\{2,-2\}$で、$-2+2-2-2+2-2-2+2-2+2-2-2$が語の例になっています。語の定義をしているときは積で書いていますが、演算を和の形で書いているときはプラスとマイナスで繋ぎまくった式が語にあたります。
部分群の生成を定義しよう
さてさて、ようやく生成の定義です。$G$を群、$S \subset G$を部分群とは限らない部分集合としましょう。このとき、$S$の元による語全体の集合を$\langle S \rangle$とします。これは$G$の部分群になり、$\langle S \rangle$を$S$によって生成された部分群といいます。
$\langle S \rangle$はどうして部分群になるのでしょうか。単位元は$0$個つなげた語のことで、演算について閉じているのは語と語をつなげても語だからで、逆元があるのは語の逆元もまた語だからです。
語たち
生成したものの性質
部分集合$S$から生成した$\langle S \rangle$ですが、これは$S$を含む最小の部分群になります！（証明略）
準同型とは？
新しい集合が出たら新しい写像を考えるよ
「群」は集合に演算が付随しているものです。数学あるあるとして、集合がベースになっている新しい概念を定義したら、その集合の間にいい感じの写像を考えるというものがあります。ここでは、そのいい感じの写像、準同型写像を説明します。早速定義します！
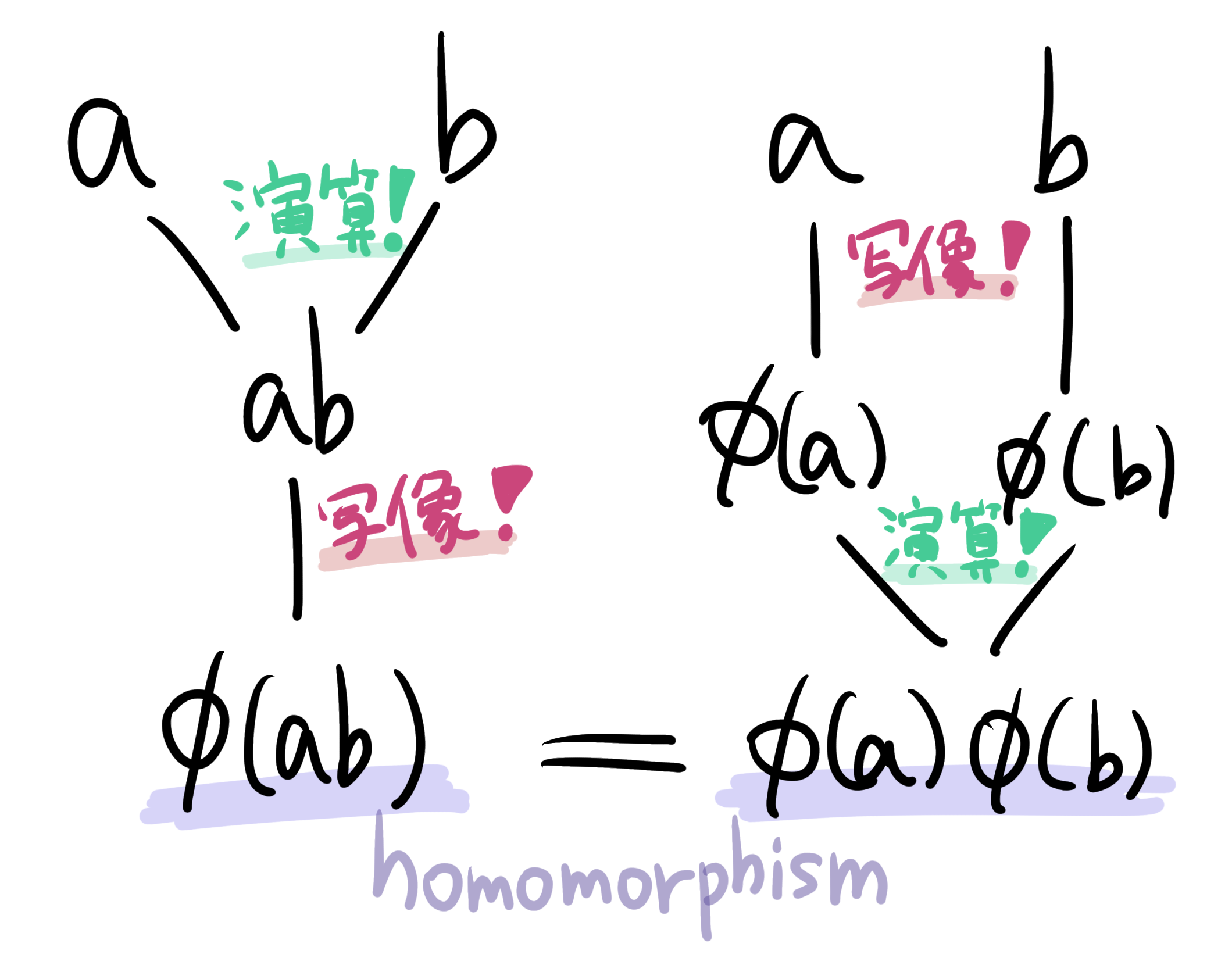
$G_1,G_2$を群, $\phi:G_1 \rightarrow G_2$を写像とする. このとき, 任意の$G$の元$x,y$について $\phi(xy)=\phi(x)\phi(y)$が成立するとき, $\phi$は準同型であるという.
この定義は「演算してから送っても、送ってから演算しても結果がおなじ」 「演算と写像で送る操作が交換可能」と咀嚼して下さい。準同型とは、群に備わっている演算と相性がいい写像、ということです。群の「構造」が大事になる話です。
演算と写像が交換可能
準同型写像は、代数学における「いい感じの写像」を包括しています。例を3つほど貼っておきます。（私の 別記事 から持ってきました。手抜き最高！！！）
この例を見て、準同型写像というのは大事な概念なんだ... とがんばって刷り込んで下さい。
開区間$I=(0,1)$上の$C^{\infty}$級関数全体を$C$とします。また$f,g \in C, x \in (0,1)$とするとき、その和$f+g$を$(f+g)(x)=f(x)+g(x)$で定めます。するとこれは$f+g \in C$で、この演算で$C$は群となります。
このとき、微分を行う写像 $\frac{d}{dx}:C \rightarrow C ;$ $ f \mapsto f'$は準同型となります。
（$\frac{d}{dx}(f+g)=\frac{df}{dx}+\frac{dg}{dx}$）
$\mathbb{R}_>=\{r\in \mathbb{R} | r > 0 \}$とします。指数関数 $\exp : \mathbb{R} \rightarrow \mathbb{R}_>$は準同型写像です。
$\exp(x+y)=\exp(x)\exp(y)$が成立していますね。定義域では「和」が群の演算、値域では「積」が群の演算になっていることに注意してください。
正則行列の行列式を求める写像$\det:\mathrm{GL}_n(\mathbb{R}) \rightarrow \mathbb{R} \setminus \{0\}$は準同型写像となります。
アイキャッチ
準同型写像のかんたんな性質を見る
準同型について、つぎの重要な事実があります。この記事のキモです。
$G_1,G_2$を群, $1_{G_1}$を$G_1$の単位元, $1_{G_2}$を$G_2$の単位元, $\phi:G_1 \rightarrow G_2$を準同型写像とする. このとき, 次が成立する.
- $\phi(1_{G_1})=1_{G_2}$.
- $x \in G_1$とするとき, $\phi(x^{-1})=\phi(x)^{-1}$.
証明します。面倒なので 画像で。
せっかく数式が使えるサイトで何してるんだろうな
さてこの、「単位元を単位元に送る」、「逆元を逆元に送る」という性質ですが、「準同型は構造を保つ」という示唆の一端となっています。
急に出てきてもよくわからないですよね
いきなり準同型とかいう新しい概念を出されても、それについて調べるモチベーションなんてそんなにすぐ湧いてこないと思います。いや普通に大事そうに見えるか それを緩和するためにも準同型を調べるメリットについて書いていこうと思います。（ここの部分はよくわからなくても大丈夫な話です）
間接的に調べる
大学数学あるあるなのですが、$\mathrm{A}$を調べたいと思った時に、$\mathrm{A}$自体を調べるのではなく、$\mathrm{A}$の情報を持ったなにかを調べるというのがあります。
例えば空でない集合$X$があったとき、一元集合$\{e\}$から$X$への写像全体$\mathrm{Map}(\{e\},X)$を考えます。これは、$X$の情報をそのまま保持しています。
どういうことでしょうか。一元集合$\{e\}$から$X$への写像というのは、ただひとつの元$e$に対して$X$の元をひとつ定めたものです。$X$の元$x$に対して、$f(e)=x$となる写像$f:\{e\} \rightarrow X$を考えると、この$f$が持っている情報というのは、「$e$の行き先」というひとつの情報です（定義域とかそういう情報もありますけど）。$e$の行き先の情報というのは、要するに$X$の元一個分の情報になります。さらに言えば、「一元集合$\{e\}$から$X$への写像」は実質的に「$X$の元と同一視できる」ということになります。
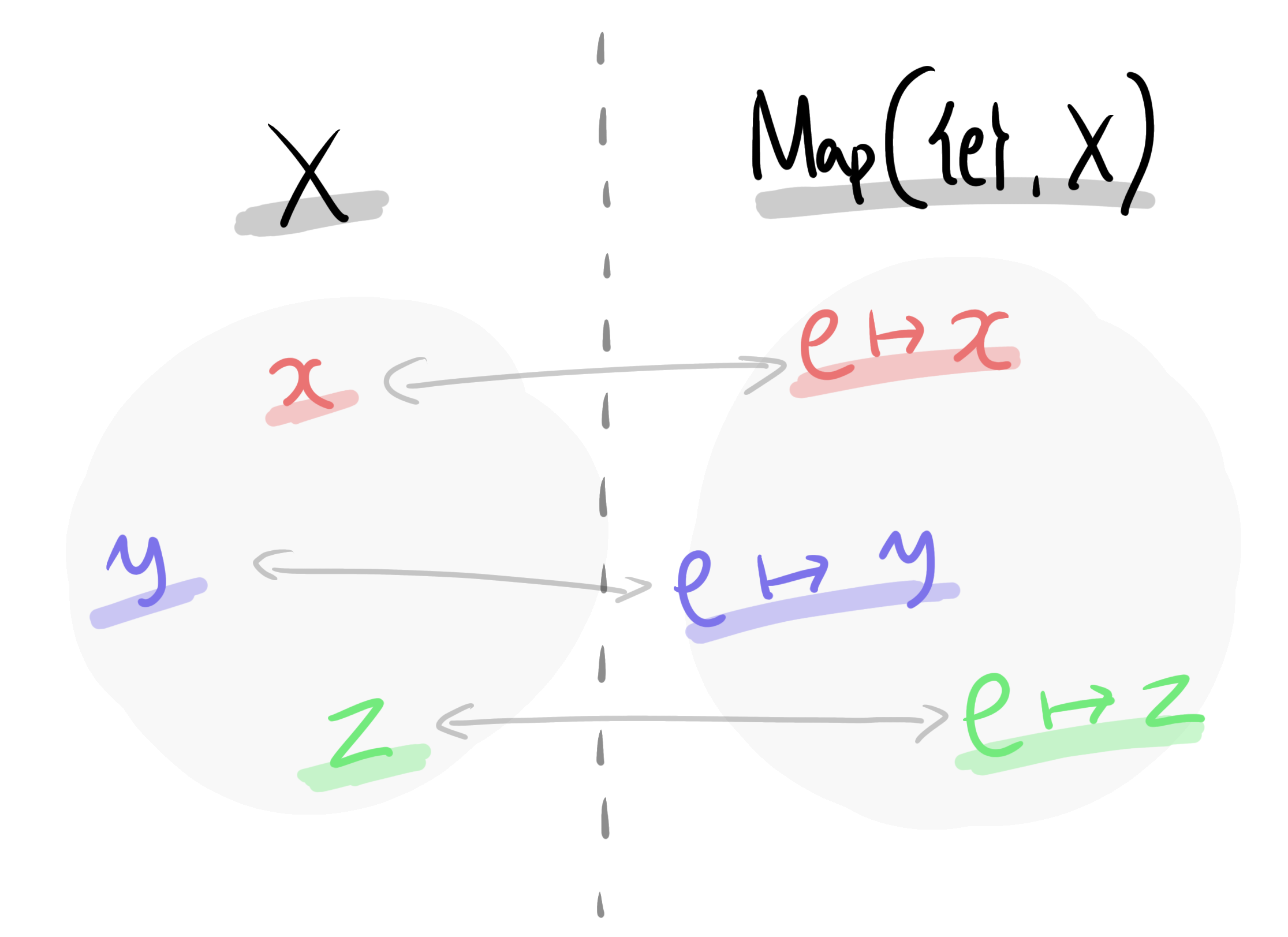ナイス1対1対応
もうちょっとフォーマルに言えば、$X$と$\mathrm{Map}(\{e\},X)$の間には全単射がある、ということです。$\mathrm{Map}(\{e\},X)$が$X$の情報を含んでいるというこの事実から、$X$そのものを考えるのではなく、$X$が絡んだ写像を考えることの意義がわかっていただけると思います。
じゃあ準同型を調べると何がわかるの
準同型について、たとえば次のような性質があります。
$G_1,G_2$を群, $\phi:G_1 \rightarrow G_2$を全射な準同型写像とする.
このとき, $G_1$が可換なら$G_2$も可換.
証明はかんたんです。これも図に投げます。
この命題は、可換群から自身への全射準同型の存在が、自身への可換性を説明するというものです。$G_1$から$G_2$への全射準同型が存在するというのは、$G_1$が$G_2$の情報を内包している、また$G_1$は$G_2$に、ちょっと似ている部分がある、というくらいに思ってよいと思います。このように、異なる群同士の関係を考察するとか、似てる群を使って性質を取り出すとか、そういうことができるのが準同型です。
本音
なんとか頑張って言葉をひねり出して準同型を調べるモチベーションを説明しましたが、準同型は群とセットの概念といってよく、準同型は群を調べる「手段」というよりむしろ、準同型自体も調べるのが「目的」といってよい概念です。群論をしたいと思ったとき、「どうして準同型写像を調べるんだろう」と思うことは「どうして群を調べるんだろう」と思うのとほぼ同じようなものだと思います。なのでまあ、準同型写像は、とりあえず受け入れて下さい（ここまで書いておいてなんだよ）
群の同型
準同型は準同型でも、「同型」と呼ばれるものがあります。これは異なる作り方をした$2$つの群が、実質的に同じものであるとみなすことができる概念です。先ほどは全射準同型の存在が、群がちょっと似ているとか、そういう風に見れると書きましたが、同型とは全単射な準同型のことです。これはちょっと似ているどころの話ではありません。群論の世界では全単射な準同型の存在をもって、その$2$つの群を同じ群とみなします。
これがやりたかっただけ
さて、同型をちゃんと定義してみましょう。
$G_1,G_2$を群, $\phi:G_1 \rightarrow G_2$を写像とする. このとき$\phi$が同型であるとは, $\phi$が逆写像を持ち, $\phi$と$\phi^{-1}$も準同型であることである. また2つの群の間に同型が存在することを$G_1 \cong G_2$で表す。
（全単射な準同型の存在が～とか書いておきながら、そうは定義していませんね。これは個人的な好みからです。位相空間論の話ですが、「全単射な連続写像」があっても同相写像と限らないからです。まあ群論では関係のない話です。群論だったら次の事実があるので大丈夫です）
$G_1,G_2$が群で, $\phi:G_1 \rightarrow G_2$が全単射な準同型写像であるなら, $G_1 \cong G_2$が成立する.
同型であることは、実は全単射な準同型が存在することを示せばそれでわかる、という主張です。証明は次のような感じです。
これで議論がちょっとラクになりますね。
同じ群とみなすってなに
違うものを同じとみなすというのは、数学をやっているとよく行うことです。中学数学などで図形の合同について学んだと思います。反転させたり回転させたり平行移動したりすればピッタリ重なる場合に、$2$つの図形は合同であると呼んでいたわけです。この「合同」という関係が、実際は座標が異なる点たち（つまり、集合としては違うものであるはず）でも動かしてピッタリ重なれば同じであるという価値観を表すわけです。
群の同型も同じです。実際は異なる集合である$2$つの群も、演算の構造がピッタリ重なれば同じ群という価値観を与えています。同型の例を見てみましょう。（また別の記事からコピーしてきました）
そうなってほしいと思いますので当然といえば当然ですが、群$G$は自分自身と同型です。$G \cong G$です。しかし、同型の作り方は工夫することができますし、しないこともできます。
例えば恒等写像$\mathrm{id}_G:G \rightarrow G$が同型です。それとは別に内部自己同型というものがあります。それは、$G$の元$g$を固定して、写像の対応$x\mapsto gxg^{-1}$を考えるというものです。これも同型写像です。どうしてこれが同型になるかは、練習で示してみてください。
$S_3$の部分群として、$(123)$で生成される部分群$H=\{1,(123),(132)\}$を考えます。これは$\mathbb{Z}/3\mathbb{Z}$と同型になります。なんか、そんな気がしますね（？）
ベクトル空間は、スカラー倍の演算を無視すると可換群とみなせます。$\mathbb{R}$ベクトル空間$\mathbb{R}^2$は和について群になりますが、この群は$\mathbb{C}$と同型です。そりゃそうかな、という感じです。$(x,y)$と$x+iy$とを対応させれば良いですね。（$i$は虚数単位を表すとします）
同型でない例も見ておきましょう。
$n \ne m$であるとき、$\mathbb{Z}/n\mathbb{Z}$と$\mathbb{Z}/m\mathbb{Z}$は同型となりません。なぜなら濃度が違うからですね。（そもそも全単射が存在しない）
濃度が同じでも同型でない例は 別の記事 で紹介しています。（前提知識がこの記事より少し多いです）
同型で区別をするとできること
同型なら同じものとみなす価値観は、群を強力に「分類」します。Mathpedia に、有限群を同型なものが同じ、同型でないものは違う、という価値観に基づいた分類をしたページがあります。覗いてみて下さい。（ 有限群の分類(位数1~100) - Mathpedia ）
この記事でやりたかったことに入ります
群の生成と準同型を、ど～～～～～しても同じ記事で解説したかったのです。準同型を調べる必要性を解いたのもそのためです。この$2$つを一緒に説明する記事を書きてえな～～～～～と2年くらい思っていたのが執筆のモチベーションでした。
そうです。「群の生成」という概念が、準同型を調べることにおいて非常に役立つのです！！！
観察してみよう
ひとまずの目標として、次の問題を解いてみましょう。
$\mathbb{Z}$から$\mathbb{Z}$への準同型をすべて特定せよ.
すべての準同型を特定するのって、どうすればいいんだ～～～という感じです。
ここでひとつアイデアを出しましょう。
準同型$\phi : \mathbb{Z} \rightarrow \mathbb{Z}$が、$\phi(1)=a$だったとしましょう。このとき、たとえば$\phi(4)$の値って、決まってしまいますよね。
なぜなら準同型は、演算と写像で送る操作が交換可能であるということですので、$\phi(4)=\phi(1+1+1+1)=\phi(1)+\phi(1)+\phi(1)+\phi(1)=a+a+a+a=4a$ということです。
そして、たとえば$\phi(-3)$の値も決まってしまいますよね。逆元をとる操作と写像で送る操作も交換可能でした。それを使うと $\phi(-3)=\phi(-1)+\phi(-1)+\phi(-1)=-\phi(1)-\phi(1)-\phi(1)=-a-a-a=-3a$がわかります。
さあ、ここまででわかりましたね。$\phi(1)$の値さえ決まればよかったのです。それはどうしてか。これは$\mathbb{Z}$が$\{1\}$によって生成されるからです。$\phi(1)$の値が$a$のとき、$\phi$は整数を$a$倍する写像になります。つまり、$\mathbb{Z}$から$\mathbb{Z}$への準同型全体は、$a$倍写像（$a\in\mathbb{Z}$）の全体ことだとわかりました。
ではこの、$\phi(1)$の値だけを考えたアイデアを定式化する命題を見てみましょう！
これを紹介したかった
$G_1,G_2$を群, $\phi_1, \phi_2:G_1 \rightarrow G_2$を準同型写像とし, $G_1$は部分集合$S$によって生成されているとする.
このとき, 任意の$S$の元$x$に対して$\phi_1(x)=\phi_2(x)$が成立していれば, $\phi_1=\phi_2$が成立する.
証明してみます！画像で
ゴリ押し
こういうの線形代数にありましたよね
線形代数の感動ポイントとして、ベクトル空間からベクトル空間への線形写像は基底の元の行き先さえ決めてしまえば定まってしまう、というのがあります。これの群論版ということですね。
もう少しだけ問題を解いてみよう
$\mathbb{Z}$から$\mathbb{Z}$への同型をすべて特定せよ.
今度は同型です。さっきの定理関係ないんですが一応証明しておきましょう（それでいいのか）。これは先程の事実の系として得ることができます。
ゆるい整数問題
$3$次対称群$S_3$から$\mathbb{R} \setminus \{0\}$への準同型をすべて特定せよ.
$S_3$を生成する元を考えるとかなりラクできます。解き方は次のような感じです。
1枚目
2枚目
まとめ
ここまで読んでいただきありがとうございました。私はいわゆる雪江代数で代数学を学んでいたのですが、B1だった当時 群の生成が語(word)で定義されていたことで混乱していた同級生を見ていました。というのもあり、雪江代数を読んでいて詰まるポイントを記事とかで減らせるといいなぁなどと思っていました。この記事が詰みポイント解消の一助になれば嬉しいです。
語で定義することのメリットとして、生成してる感が出る（？）というのと、上で紹介しました、生成する部分集合の行き先だけ見れば準同型が定まる事実が直感的になるというものがあると思います。この記事でやりたかったのはそれなので、語を用いた定義を採用しました。まあそれをやらないんだったら自身を含む部分群すべての共通部分で定義したいのですが
もし面白かったという方は記事の高評価よろしくお願いします！ それでは～～～
