写像の連続性を測るもの
はじめに
距離空間の間の写像については,連続性というものを考えることができました.
本記事では,写像の連続性の ”度合い” を測ることができる「連続度」という概念を紹介します.
(人によっては「連続率」など別の呼び方をすることもあるようです.)
正確な定義はすぐ後で述べますが,大雑把に言えば,写像$f:X\to Y$の連続度とは「2点$x,x'\in X$の近さ」に対して「2点$f(x),f(x')\in Y$の近さ」を返すような写像$\omega:[0,\infty]\to[0,\infty]$のことです.
$\varepsilon$-$\delta$を知っている人向けの補足
連続度$\omega$は "$\varepsilon$-$\delta$論法の$\delta$に対して$\varepsilon$を対応させる関数$\varepsilon=\omega(\delta)$" と思えばわかりやすいかもしれません.
英語版Wikipedia
には
In general, the role of $\omega$ is to fix some explicit functional dependence of $\varepsilon$ on $\delta$ in the $(\varepsilon,\delta)$ definition of uniform continuity.という記述があります.
$f$の連続性は「$x$と$x'$が十分近ければ,$f(x)$と$f(x')$は限りなく近づく」のように説明されることがありますが,この素朴な表現を連続度の性質に翻訳した
$$ \lim_{\delta\to +0}\omega(\delta)=0$$
という条件は実際に$f$の連続性を特徴づけます.
また,$f$の連続度の値が小さいほど2点$f(x),f(x')$が近くなりやすい(=連続性が強い)と考えられるので,連続度の値の大小によって連続性の強さを定量的に記述することが可能です.
悲しいことに日本語版Wikipediaには連続度のページがないので,
英語版Wikipedia
の記述を参考にいくつかの事実を証明付きで述べたいと思います.
Wikipediaの方には本記事で扱えなかった性質もいろいろ書いてあるので,ぜひそちらも読んでみてください.
連続度による連続性の言い換え
この節では,連続度の定義を紹介し,それを用いて$\varepsilon$-$\delta$論法による連続性の定義を書き直せることを見る.
連続度の定義
連続度とは,距離空間の間の連続写像$f:X\to Y$について「$x$と$x'$の距離が$\delta$以下ならば,$f(x)$と$f(x')$の距離は$\omega(\delta)$以下である」というような近さの定量的な関係を表現するのに用いる指標$\omega:[0,\infty]\to[0,\infty]$のことである.
連続度 (modulus of continuity) とは,写像$\omega:[0,\infty]\to[0,\infty]$であって,次の2条件を満たすもののことをいう.
- $\omega$は単調増加である.
- $\delta\to +0$のとき$\omega(\delta)\to 0$である.
![連続度のグラフ!FORMULA[39][-1965623688][0]の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FZhq0Lq2rFNdgUKrLISoM.png?alt=media) 連続度のグラフ$y=\omega(x)$の例
連続度のグラフ$y=\omega(x)$の例
連続度$\omega$について,単調増加性とはさみうちの原理より
$$ 0\le\omega(0)\le\omega(\delta)\to 0\qquad (\delta\to +0),$$
つまり$\omega(0)=0$が成り立つ.
連続度の定義のうち「$\delta\to +0$のとき$\omega(\delta)\to 0$である.」は,極限の定義から
- 任意の$\varepsilon\in(0,\infty)$に対してある$\delta\in(0,\infty)$が存在して,任意の$r\in(0,\delta]$に対して$\omega(r)\le\varepsilon$が成り立つ.
と表せるが,この条件は($\omega$の単調増加性から)より簡単な条件
- 任意の$\varepsilon\in(0,\infty)$に対してある$\delta\in(0,\infty)$が存在して,$\omega(\delta)\le\varepsilon$が成り立つ.
で置き換えることができる.
距離空間の間の写像$f:X\to Y$と単調増加な写像$\omega:[0,\infty]\to[0,\infty]$および点$x\in X$について,次の2条件は互いに同値であることを示せ.
- $d_X(x,x')\le\delta$を満たす任意の$x'\in X$と$\delta\in[0,\infty]$に対して,$d_Y(f(x),f(x'))\le\omega(\delta)$が成り立つ.
- 任意の$x'\in X$に対して,$d_Y(f(x),f(x'))\le\omega(d_X(x,x'))$が成り立つ.
- $(1)\Rightarrow(2)$:$x'\in X$に対して,$\delta:=d_X(x,x')$とおいて (1) を使えばよい.
- $(2)\Rightarrow(1)$:$x'\in X$と$\delta\in[0,\infty]$が$d_X(x,x')\le\delta$を満たすとき,$\omega$の単調性より$d_Y(f(x),f(x'))\le \omega(d_X(x,x'))\le \omega(\delta)$が成り立つ.
連続度$\omega$があれば,写像$f:X\to Y$について「不等式$d_Y(f(x),f(x'))\le\omega(d_X(x,x'))$が常に成り立つ」という性質($\omega$-連続性)が成り立つかどうかによって,$f$の連続性の強さを定量的に表現できる.
$(X,d_X),(Y,d_Y)$を距離空間,$\omega$を連続度とし,写像$f:X\to Y$を考える.
- $f$が点$x\in X$において$\omega$-連続 ($\omega$-continuous) であるとは,任意の$x'\in X$に対して不等式$d_Y(f(x),f(x'))\le\omega(d_X(x,x'))$が成り立つことをいう.
- $f$が$\omega$-連続であるとは,$f$が$X$の任意の点において$\omega$-連続であること,つまり任意の$x,x'\in X$に対して不等式$d_Y(f(x),f(x'))\le\omega(d_X(x,x'))$が成り立つことをいう.
![!FORMULA[94][1644233115][0]-連続写像のグラフの例(青線)。!HTML[2][1885234][0]グラフが赤い領域に含まれることが!FORMULA[95][1644233115][0]-連続性を意味する(!FORMULA[96][1644233115][0]は図1の連続度)](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fe2ylkXTwznElJqCr7Nju.gif?alt=media) $\omega$-連続写像のグラフの例(青線)。
$\omega$-連続写像のグラフの例(青線)。
グラフが赤い領域に含まれることが$\omega$-連続性を意味する($\omega$は図1の連続度)
$\alpha\in(0,1]$とする.このとき,連続度$\omega(\delta):=L\delta^\alpha$($L$は正の実数)に対する$\omega$-連続性は$\alpha$-ヘルダー連続性とよばれる.
![ヘルダー連続写像のグラフ(青線)。!HTML[3][58441851][0]!FORMULA[102][1242830142][0]が大きいほど局所的な変動が強く制限される](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FxVkfvCfaqmWkI2LiMXln.gif?alt=media) ヘルダー連続写像のグラフ(青線)。
ヘルダー連続写像のグラフ(青線)。
$\alpha$が大きいほど局所的な変動が強く制限される
特に,$1$-ヘルダー連続性のことをリプシッツ連続性という.
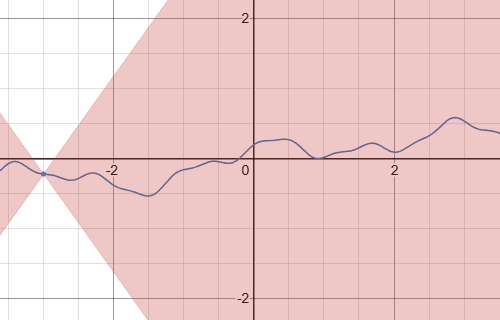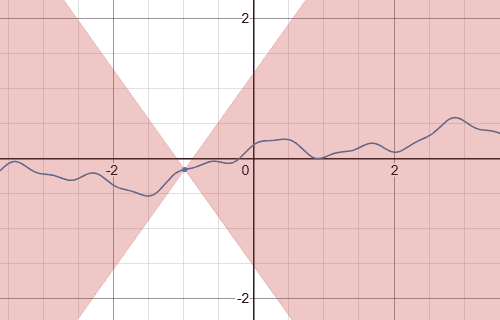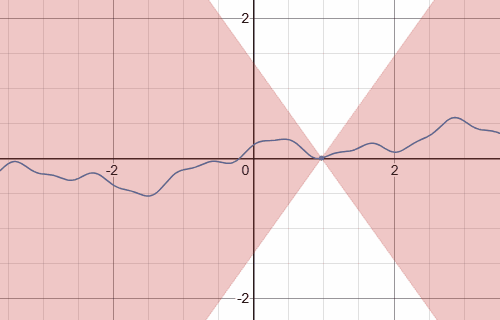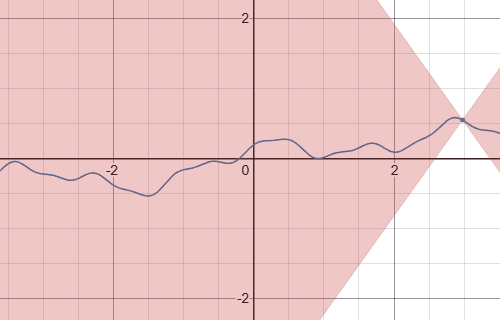 リプシッツ連続写像のグラフ(青線)
リプシッツ連続写像のグラフ(青線)
最適連続度
ここでは距離空間の間の写像$f:X\to Y$に対して,「$x$と$x'$の距離が$\delta$以下ならば,$f(x)$と$f(x')$の距離は$\omega(\delta)$以下である」という性質を満たす写像$\omega:[0,\infty]\to[0,\infty]$のうち最小のものを構成することを考える.
距離空間の間の写像$f:X\to Y$を考える.
- 点$x\in X$に対して,$f$の$x$における最適連続度 (the optimal modulus of continuity)$\omega_{f,x}:[0,\infty]\to[0,\infty]$を次式で定める.
$$ \omega_{f,x}(\delta):=\sup(\{d_Y(f(x),f(x'))\mid x'\in X,\ d_X(x,x')\le \delta\}) \qquad (\delta\in[0,\infty]).$$ - $f$の最適連続度$\omega_{f}:[0,\infty]\to[0,\infty]$を次式で定める.
$$ \omega_{f}(\delta):=\sup(\{d_Y(f(x),f(x'))\mid x,x'\in X,\ d_X(x,x')\le \delta\}) \qquad (\delta\in[0,\infty]).$$
最適連続度$\omega_{f,x},\omega_{f}$は
$$ \lim_{\delta\to+0}\omega_{f,x}(\delta)=0, \qquad \lim_{\delta\to+0}\omega_{f}(\delta)=0 $$
を満たすとは限らず,したがって冒頭で述べた意味での連続度になっているとは限らない.
後述するように,上の式が成り立つことは,$f$の$x$における連続性や一様連続性と同値になる.
距離空間の間の写像$f:X\to Y$と点$x\in X$に対して,最適連続度$\omega_{f,x}$を考える.
- $\omega_{f,x}(0)=0$である.
- $\omega_{f,x}$は単調増加である.
- 任意の$x'\in X$に対して$d_Y(f(x),f(x'))\le\omega_{f,x}(d_X(x,x'))$が成り立つ.
- 連続度$\omega$について,$f$が$x$において$\omega$-連続であれば,任意の$\delta\in[0,\infty]$に対して$\omega_{f,x}(\delta)\le\omega(\delta)$が成り立つ.
- $d_X(x,x')\le 0$のとき$x'=x$より$d(f(x),f(x'))=0$だから,$\omega_{f,x}(0)=\sup(\{0\})=0$である.
- 集合$\{d_Y(f(x),f(x'))\mid x'\in X,\ d_X(x,x')\le \delta\}$は$\delta$に関して単調増加だから,$\omega_{f,x}$も単調増加である.
- $\omega_{f,x}$の定義より,$d_X(x,x')\le\delta$を満たす任意の$x'\in X$と$\delta\in[0,\infty]$に対して$d_Y(f(x),f(x'))\le \omega_{f,x}(\delta)$が成り立つから,特に$\delta:=d_X(x,x')$と取れば良い.
- $x$における$\omega$-連続性より,$d_X(x,x')\le\delta$を満たす任意の$x'\in X$に対して$d_Y(f(x),f(x'))\le \omega(d_X(x,x'))\le \omega(\delta)$が成り立つから,$\omega_{f,x}$の定義より$\omega_{f,x}(\delta)\le\omega(\delta)$を得る.
距離空間の間の写像$f:X\to Y$に対して,最適連続度$\omega_{f}$を考える.
- $\omega_{f}(0)=0$である.
- $\omega_{f}$は単調増加である.
- 任意の$x,x'\in X$に対して$d_Y(f(x),f(x'))\le\omega_{f}(d_X(x,x'))$が成り立つ.
- 連続度$\omega$について,$f$が$\omega$-連続であれば,任意の$\delta\in[0,\infty]$に対して$\omega_{f}(\delta)\le\omega(\delta)$が成り立つ.
- $d_X(x,x')\le 0$のとき$x'=x$より$d(f(x),f(x'))=0$だから,$\omega_{f}(0)=\sup(\{0\})=0$である.
- 集合$\{d_Y(f(x),f(x'))\mid x,x'\in X,\ d_X(x,x')\le \delta\}$は$\delta$に関して単調増加だから,$\omega_{f}$も単調増加である.
- $\omega_{f}$の定義より,$d_X(x,x')\le\delta$を満たす任意の$x,x'\in X$と$\delta\in[0,\infty]$に対して$d_Y(f(x),f(x'))\le \omega_{f}(\delta)$が成り立つから,特に$\delta:=d_X(x,x')$と取れば良い.
- $\omega$-連続性より,$d_X(x,x')\le\delta$を満たす任意の$x,x'\in X$に対して$d_Y(f(x),f(x'))\le \omega(d_X(x,x'))\le \omega(\delta)$が成り立つから,$\omega_{f}$の定義より$\omega_{f}(\delta)\le\omega(\delta)$を得る.
$(X,d_X),(Y,d_Y)$を距離空間とし,写像$f:X\to Y$を考える.このとき,次式が成り立つ:
$$\omega_f(\delta)=\sup(\{\omega_{f,x}(\delta)\mid x\in X\}) \qquad (\delta\in[0,\infty]).$$
$\delta\in [0,\infty]$を任意に取る.
- $x\in X$を任意に取る.このとき$d_X(x,x')\le\delta$を満たす任意の$x'\in X$に対して
$$ d_Y(f(x),f(x'))\le\omega_f(d_X(x,x'))\le\omega_f(\delta)$$
が成り立つから,$x'$の任意性より$\omega_{f,x}(\delta)\le\omega_f(\delta)$となる.$x$は任意だったから,$\omega_f(\delta)\ge \sup(\{\omega_{f,x}(\delta)\mid x\in X\})$を得る. - $d_X(x,x')\le\delta$を満たす任意の$x,x'\in X$に対して
$$ d_Y(f(x),f(x'))\le \omega_{f,x}(d_X(x,x'))\le \omega_{f,x}(\delta)\le \sup(\{\omega_{f,x}(\delta)\mid x\in X\})$$
が成り立つから,$x,x'$の任意性より$\omega_{f}(\delta)\le \sup(\{\omega_{f,x}(\delta)\mid x\in X\})$を得る.
連続性の特徴づけ
$(X,d_X),(Y,d_Y)$を距離空間,$x\in X$とし,写像$f:X\to Y$を考える.このとき,次の2条件は同値である.
- $f$は$x$において連続である.
- ある連続度$\omega$が存在して,$f$は$x$において$\omega$-連続である.
$(1)\Rightarrow(2)$:詳細
最適連続度$\omega_{f,x}:[0,\infty]\to[0,\infty]$が
$$ \lim_{\delta\to +0}\omega_{f,x}(\delta)=0$$
を満たすことを示せばよい.$\varepsilon\in(0,\infty)$を任意に取ると,$f$の$x$における連続性より「$d_X(x,x')\le\delta$を満たす任意の$x'\in X$に対して$d_Y(f(x),f(x'))\le\varepsilon$が成り立つ」という性質を満たす$\delta\in(0,\infty)$が取れる.この性質は「$\varepsilon$が集合
$$ \{d_Y(f(x),f(x'))\mid x'\in X,\ d_X(x,x')\le\delta\} $$
の上界であること」を表しているので,$\omega_{f,x}(\delta)\le \varepsilon$が示された.$(2)\Rightarrow(1)$:詳細
$\varepsilon\in(0,\infty)$を任意に取る.このとき$\displaystyle\lim_{\delta\to +0}\omega(\delta)=0$であることから$\omega(\delta)\le \varepsilon$を満たす$\delta\in(0,\infty)$が取れて,$d_X(x,x')\le \delta$を満たす任意の$x'\in X$に対して$$ d_Y(f(x),f(x'))\le \omega(d_X(x,x'))\le \omega(\delta)\le\varepsilon $$が成り立つ.したがって,$f$は$x$において連続であることが示された.
一方で,「$f$が($X$の任意の点において)連続であること」と「ある連続度$\omega$が存在して,$f$が($X$の任意の点において)$\omega$-連続であること」は同値ではない.
これらの条件は,上の命題を踏まえるとそれぞれ次のように言い換えられる:
$f$が連続である
$\iff$ 任意の$x\in X$に対して,ある連続度$\omega_x$が存在して,$f$は$x$において$\omega_x$-連続であるある連続度$\omega$が存在して,$f$が$\omega$-連続である
$\iff$ ある連続度$\omega$が存在して,任意の$x\in X$に対して,$f$は$x$において$\omega$-連続である
が,連続度が点$x\in X$に依存するかどうかの違いがあるからである(前者は各$x$に対して別々の連続度を取ることができるのに対して,後者はすべての$x$に共通な連続度の存在を要請している).
このことから推測されるように,後者の条件に対応するのは,単なる連続性ではなく一様連続性である.
$(X,d_X),(Y,d_Y)$を距離空間とし,写像$f:X\to Y$を考える.このとき,次の2条件は同値である.
- $f$は一様連続である.
- ある連続度$\omega$が存在して,$f$は$\omega$-連続である.
$(1)\Rightarrow(2)$:詳細
最適連続度$\omega_{f}:[0,\infty]\to[0,\infty]$が
$$ \lim_{\delta\to +0}\omega_{f}(\delta)=0$$
を満たすことを示せばよい.$\varepsilon\in(0,\infty)$を任意に取ると,$f$の一様連続性より「$d_X(x,x')\le\delta$を満たす任意の$x,x'\in X$に対して$d_Y(f(x),f(x'))\le\varepsilon$が成り立つ」という性質を満たす$\delta\in(0,\infty)$が取れる.この性質は「$\varepsilon$が集合
$$ \{d_Y(f(x),f(x'))\mid x,x'\in X,\ d_X(x,x')\le\delta\} $$
の上界であること」を表しているので,$\omega_{f}(\delta)\le \varepsilon$が示された.$(2)\Rightarrow(1)$:詳細
$\varepsilon\in(0,\infty)$を任意に取る.このとき$\displaystyle\lim_{\delta\to +0}\omega(\delta)=0$であることから$\omega(\delta)\le \varepsilon$を満たす$\delta\in(0,\infty)$が取れて,$d_X(x,x')\le \delta$を満たす任意の$x,x'\in X$に対して
$$ d_Y(f(x),f(x'))\le \omega(d_X(x,x'))\le \omega(\delta)\le\varepsilon $$
が成り立つ.したがって,$f$は一様連続であることが示された.
写像$f:\mathbb{R}\ni x\mapsto x^2\in\mathbb{R}$について,以下の問に答えよ.
- $x\in\mathbb{R}$と$\delta\in[0,\infty]$に対して,$\omega_{f,x}(\delta)=\delta(\delta+2|x|)$が成り立つことを示せ.
- $f$が一様連続でないことを示せ.
解答例
$\delta=0,\infty$の場合は個別に考えることで容易に示せるから,以下$\delta\in(0,\infty)$の場合のみ考える.
- $|x-y|\le\delta$を満たす任意の$y\in\mathbb{R}$に対して
$$ |f(x)-f(y)|=|x^2-y^2|=|x-y||x+y|\le \delta(|y-x|+2|x|)\le \delta(\delta+2|x|)$$
が成り立つから,$\omega_{f,x}(\delta)\le\delta(\delta+2|x|)$である. - $y\in\mathbb{R}$を次式で定める.
$$ y:=\begin{cases}x+\delta&(\text{$x\ge 0$ の場合}),\\x-\delta&(\text{$x<0$ の場合}).\end{cases} $$
このとき$|x-y|=\delta$かつ$y^2=x^2+2|x|\delta+\delta^2$が成り立つから
$$ |f(x)-f(y)|=|x^2-y^2|=2|x|\delta+\delta^2=\delta(\delta+2|x|),$$
よって$\omega_{f,x}(\delta)\ge\delta(\delta+2|x|)$である.
- $|x-y|\le\delta$を満たす任意の$y\in\mathbb{R}$に対して
解答例
(1) より,$\delta\in[0,\infty]$に対して\begin{align*} \omega_f(\delta) =\sup_{x\in\mathbb{R}}\omega_{f,x}(\delta) =\sup_{x\in\mathbb{R}}\delta(\delta+2|x|) =\begin{cases} 0 & (\text{$\delta=0$ の場合}), \\ \infty & (\text{$\delta>0$ の場合}) \end{cases} \end{align*}
が成り立つから,$\displaystyle\lim_{\delta\to +0}\omega_f(\delta)=\infty$であり,$f$は一様連続でない.
$(X,d_X),(Y,d_Y)$を距離空間とし,写像$f:X\to Y$の最適連続度を$\omega_{f}$とする.
このとき$f$がディニ連続 (Dini-continuous) であるとは
$$ \int_0^1\frac{\omega_f(t)}{t}\,dt<\infty$$
が成り立つことをいう.次の問に答えよ.
- $\alpha\in(0,1]$とする.$f$が$\alpha$-ヘルダー連続ならば,$f$はディニ連続でもあることを示せ.
- $f$がディニ連続ならば,$f$は一様連続でもあることを示せ.
(※ ヘルダー連続でないディニ連続写像の例 )
解答例
$\alpha$-ヘルダー連続性より,ある$L\in(0,\infty)$が存在して,任意の$t\in[0,\infty]$に対して$\omega_f(t)\le Lt^\alpha$が成り立つ.よって
\begin{align*} \int_0^1\frac{\omega_f(t)}{t}\,dt &\le\int_0^1 Lt^{\alpha-1}\,dt =\frac{L}{\alpha}<\infty. \end{align*}解答例
もし$f$が一様連続でなければ,ある$\varepsilon_0\in(0,\infty)$が存在して,任意の$\delta\in(0,\infty)$に対して$\omega_f(\delta)>\varepsilon_0$が成り立つ.このとき
$$ \int_0^1\frac{\omega_f(t)}{t}\,dt\ge \int_0^1\frac{\varepsilon_0}{t}\,dt=\infty$$
となって$f$のディニ連続性に矛盾する.
連続度の性質
$(X,d_X),(Y,d_Y)$を距離空間,$x\in X$とし,連続度$\omega_1,\omega_2$は任意の$\delta\in[0,\infty]$に対して
$$ \omega_1(\delta)\le\omega_2(\delta) $$
を満たすとする.このとき,写像$f:X\to Y$が$x$において$\omega_1$-連続であれば,$f$は$x$において$\omega_2$-連続でもある.
$x'\in X$を任意に取ると,$f$の$x$における$\omega_1$-連続性などから
$$ d_Y(f(x),f(x'))\le \omega_1(d_X(x,x'))\le \omega_2(d_X(x,x')) $$
が成り立つ.したがって,$f$は$x$において$\omega_2$-連続である.
$(X,d_X),(Y,d_Y),(Z,d_Z)$を距離空間,$x\in X$,$\omega_1,\omega_2$を連続度とする.
このとき,写像$f:X\to Y$が$x$において$\omega_1$-連続で,かつ写像$g:Y\to Z$が$f(x)$において$\omega_2$-連続であれば,合成写像$g\circ f$は$x$において${\omega_2}\circ{\omega_1}$-連続である.
$x'\in X$を任意に取ると
\begin{align*}
d_Z((g\circ f)(x),(g\circ f)(x'))
&=d_Z(g(f(x)),g(f(x'))) \\
&\le \omega_2(d_Y(f(x),f(x'))) \\
&\le \omega_2(\omega_1(d_X(x,x'))) \\
&=({\omega_2}\circ{\omega_1})(d_X(x,x'))
\end{align*}
が成り立つから,$g\circ f$は$x$において${\omega_2}\circ{\omega_1}$-連続である.
$K\in\{\mathbb{R},\mathbb{C}\}$とし,$(X,d_X)$を距離空間,$(W,\|\cdot\|_W)$を$K$-ノルム空間とする.このとき,次のことが成り立つ.
- $x\in X$,$a,b\in K$とし,$\omega_1,\omega_2$を連続度とする.
このとき写像$f,g:X\to W$が$x$においてそれぞれ$\omega_1$-連続,$\omega_2$-連続であれば,$af+bg$は$x$において$|a|\omega_1+|b|\omega_2$-連続である. - $x\in X$と連続度$\omega$に対して,次の集合は$W^X$の凸部分集合である:
\begin{align*} C_{x,\omega}(X,W)&:=\{f\in W^X\mid \text{$f$ は $x$ において $\omega$-連続である}\}, \\ C_{\omega}(X,W)&:=\{f\in W^X\mid \text{$f$ は $\omega$-連続である}\}. \end{align*} - $x\in X$と連続度$\omega$に対して
\begin{align*} C_{x,[0,\infty)\omega}(X,W)&:=\{f\in W^X\mid \text{$f\in C_{x,L\omega}(X,W)$ を満たす $L\in[0,\infty)$ が存在する}\}, \\ C_{[0,\infty)\omega}(X,W)&:=\{f\in W^X\mid \text{$f\in C_{L\omega}(X,W)$ を満たす $L\in[0,\infty)$ が存在する}\} \end{align*}
と定め,$[{\cdot}]_{x,\omega}:C_{x,[0,\infty)\omega}(X,W)\to[0,\infty)$と$[{\cdot}]_{\omega}:C_{[0,\infty)\omega}(X,W)\to[0,\infty)$を
\begin{align*} [f]_{x,\omega}&:=\inf\{L\in[0,\infty)\mid f\in C_{x,L\omega}(X,W)\}, \\ [f]_{\omega}&:=\inf\{L\in[0,\infty)\mid f\in C_{L\omega}(X,W)\} \end{align*}
で定義する.このとき,$[{\cdot}]_{x,\omega},[{\cdot}]_{\omega}$はそれぞれ$C_{x,[0,\infty)\omega}(X,W),C_{[0,\infty)\omega}(X,W)$上のセミノルムとなる.つまり次のことが成り立つ.- 任意の$f\in C_{x,[0,\infty)\omega}(X,W)$と$a\in K$に対して,$[af]_{x,\omega}=|a|[f]_{x,\omega}$である.
(任意の$f\in C_{[0,\infty)\omega}(X,W)$と$a\in K$に対して,$[af]_{\omega}=|a|[f]_{\omega}$である.) - 任意の$f,g\in C_{x,[0,\infty)\omega}(X,W)$に対して,$[f+g]_{x,\omega}\le [f]_{x,\omega}+[g]_{x,\omega}$である.
(任意の$f,g\in C_{[0,\infty)\omega}(X,W)$に対して,$[f+g]_{\omega}\le [f]_{\omega}+[g]_{\omega}$である.)
- 任意の$f\in C_{x,[0,\infty)\omega}(X,W)$と$a\in K$に対して,$[af]_{x,\omega}=|a|[f]_{x,\omega}$である.
任意の$x'\in X$に対して
\begin{align*} \|(af+bg)(x)-(af+bg)(x')\|_W &=\|a(f(x)-f(x'))+b(g(x)-g(x'))\|_W \\ &\le |a|\|f(x)-f(x')\|_W+|b|\|g(x)-g(x')\|_W \\ &\le |a|\omega_1(d_X(x,x'))+|b|\omega_2(d_X(x,x'))\\ &=(|a|\omega_1+|b|\omega_2)(d_X(x,x')) \end{align*}
が成り立つから,$af+bg$は$|a|\omega_1+|b|\omega_2$-連続である.任意の$f,g\in C_{x,\omega}(X,W)$と$t\in[0,1]$に対して,(1)より$(1-t)f+tg$も$x$において$\omega$-連続となるから,$C_{x,\omega}(X,W)$は凸集合である.すると「凸集合たちの共通部分は凸集合である」という事実(参考:凸集合と基本性質)と次の等式
$$ C_{\omega}(X,W)=\bigcap_{x\in X}C_{x,\omega}(X,W) $$
から,$C_{\omega}(X,W)$の凸性も従う.まず注意として,$[{\cdot}]_{x,\omega},[{\cdot}]_\omega$の定義式の中にある$\inf$は$\min$で置き換えてよい.
補足:$\inf$を$\min$で置き換えてよい理由
$f\in C_{[0,\infty)\omega}(X,W)$が$[f]_{\omega}\omega$-連続であることを確かめればよい(各点における議論も同様).
$[f]_\omega$の定義から$f\in C_{L\omega}(X,W)$を満たす$L\in[[f]_\omega,[f]_\omega+1)$が存在するが,このとき任意の$\delta\in[0,\infty]$に対して$[f]_\omega\omega(\delta)\le L\omega(\delta)$が成り立つから$f$は$[f]_\omega\omega$-連続でもある.
これを踏まえると,(1) から容易に (3) が示される.簡単のため()内のみ示すが,他方も同様.- $f$は$[f]_\omega\omega$-連続だから,(1)より$af$は$|a|[f]_\omega\omega$-連続であり,$[af]_\omega\le|a|[f]_\omega$を得る.逆向きの不等式$[af]_\omega\ge|a|[f]_\omega$は,$a=0$のときは自明であり,$a\ne 0$のときは既に示した不等式
$$ \bigg[\frac{1}{a}\cdot af\bigg]_\omega\le \bigg|\frac{1}{a}\bigg|[af]_\omega $$
を整理すれば得られる. - $f$は$[f]_\omega\omega$-連続で$g$は$[g]_\omega\omega$-連続だから,(1)より$f+g$は$[f]_\omega\omega+[g]_\omega\omega$-連続であり,$[f+g]_\omega\le[f]_\omega+[g]_\omega$を得る.
- $f$は$[f]_\omega\omega$-連続だから,(1)より$af$は$|a|[f]_\omega\omega$-連続であり,$[af]_\omega\le|a|[f]_\omega$を得る.逆向きの不等式$[af]_\omega\ge|a|[f]_\omega$は,$a=0$のときは自明であり,$a\ne 0$のときは既に示した不等式
この命題の (3) から,$C_{x,[0,\infty)\omega}(X,W)$や$C_{[0,\infty)\omega}(X,W)$上の任意のノルム$\|\cdot\|$に対して,$\|\cdot\|+[\cdot]_{x,\omega}$や$\|\cdot\|+[\cdot]_{\omega}$がそれぞれ新たなノルムになることがわかる.
$(X,d_X),(Y,d_Y)$を距離空間,$x\in X$とし,$\omega$を連続度とする.
このとき,$x$において$\omega$-連続な写像の列$\seq{f_n:X\to Y}{n}$がある写像$f:X\to Y$に各点収束するならば,$f$も$x$において$\omega$-連続である.
任意の$x'\in X$に対して
\begin{align*}
d_Y(f(x),f(x'))
&\le d_Y(f(x),f_n(x))+d_Y(f_n(x),f_n(x'))+d_Y(f_n(x'),f(x')) \\
&\le d_Y(f(x),f_n(x))+\omega(d_X(x,x'))+d_Y(f_n(x'),f(x')) \\
&\to \omega(d_X(x,x')) & (n\to\infty)
\end{align*}
が成り立つから,$f$も$x$において$\omega$-連続である.
$K\in\{\mathbb{R},\mathbb{C}\}$,$(X,d_X)$を距離空間,$(W,\langle\cdot,\cdot\rangle_W)$を$K$-内積空間,$x\in X$とし,$\omega_1,\omega_2$を連続度とする.
このとき,写像$f,g:X\to W$が$x$においてそれぞれ$\omega_1$-連続,$\omega_2$-連続であり,
$$ \|f\|_\infty:=\sup_{x\in X}\|f(x)\|_W, \quad \|g\|_\infty:=\sup_{x\in X}\|g(x)\|_W $$
がいずれも有限値であれば,次の写像
$$ \langle f(\cdot),g(\cdot)\rangle_W:X\ni z\mapsto \langle f(z),g(z)\rangle_W\in K $$
は$x$において$\|g\|_\infty\omega_1+\|f\|_\infty\omega_2$-連続である.
任意の$x'\in X$に対して
\begin{align*}
|{\langle f(x),g(x)\rangle_W-\langle f(x'),g(x')\rangle_W}|
&=|{\langle f(x)-f(x'),g(x)\rangle_W+\langle f(x'),g(x)-g(x')\rangle_W}| \\
&\le \|f(x)-f(x')\|_W\|g(x)\|_W+\|f(x')\|_W\|g(x)-g(x')\|_W \\
&\le \omega_1(d_X(x,x'))\|g\|_\infty+\|f\|_\infty\omega_2(d_X(x,x')) \\
&=(\|g\|_\infty\omega_1+\|f\|_\infty\omega_2)(d_X(x,x'))
\end{align*}
が成り立つから,$\langle f(\cdot),g(\cdot)\rangle_W$は$x$において$\|g\|_\infty\omega_1+\|f\|_\infty\omega_2$-連続である.
$(X,d_X)$を距離空間,$x\in X$,$\omega$を連続度とし,$x$において$\omega$-連続な写像の空でない族$\family{f_\lambda:X\to\mathbb{R}}{\lambda\in\Lambda}$を考える.
このとき,次の写像
\begin{align*}
\inf_{\lambda\in\Lambda}f_\lambda
&:X\ni z\mapsto \inf_{\lambda\in\Lambda}f_\lambda(z)\in\mathbb{R}\cup\{-\infty\}, \\
\sup_{\lambda\in\Lambda}f_\lambda
&:X\ni z\mapsto \sup_{\lambda\in\Lambda}f_\lambda(z)\in\mathbb{R}\cup\{\infty\}
\end{align*}
の値域が$\mathbb{R}$に含まれるなら,その写像も$x$において$\omega$-連続である.
任意の$x'\in X$と$\mu\in\Lambda$に対して,次の評価
\begin{align*}
\inf_{\lambda\in\Lambda}f_\lambda(x)\le f_\mu(x)\le f_\mu(x')+|f_\mu(x)-f_\mu(x')|\le f_\mu(x')+\omega(d_X(x,x'))
\end{align*}
より
$$ \bigg|\inf_{\lambda\in\Lambda}f_\lambda(x)-\inf_{\lambda\in\Lambda}f_\lambda(x')\bigg|\le \omega(d_X(x,x')) $$
を得るから,$\displaystyle\inf_{\lambda\in\Lambda}f_\lambda$は$\omega$-連続である.$\displaystyle\sup_{\lambda\in\Lambda}f_\lambda$についても同様に示せる.
上の命題の状況で,$\omega([0,\infty))\subset[0,\infty)$であり,かつ$\displaystyle\inf_{\lambda\in\Lambda}f_\lambda(x_0)\in\mathbb{R}$を満たす$x_0\in X$が存在するならば,$\displaystyle\inf_{\lambda\in\Lambda}f_\lambda$の値域は$\mathbb{R}$に含まれる.
実際,$z\in X$と$\mu\in\Lambda$を任意に取ると
$$ \inf_{\lambda\in\Lambda}f_\lambda(x_0)-f_\mu(z)\le f_\mu(x_0)-f_\mu(z)\le \omega(d_X(x_0,z)) $$
より
$$ -\infty<\inf_{\lambda\in\Lambda}f_\lambda(x_0)-\omega(d_X(x_0,z))\le \inf_{\lambda\in\Lambda}f_\lambda(z) $$
を得る.$\displaystyle\sup_{\lambda\in\Lambda}f_\lambda$についても同様.
連続度の定義から単調増加性を除くこともあるが,その場合であっても適当に上限を取ることで単調増加にすることができる.
写像$\omega:[0,\infty]\to[0,\infty]$が次の2条件を満たすとする:
- $\omega(0)=0$.
- $\delta\to +0$のとき$\omega(\delta)\to 0$である.
このとき,次式で定める写像$\tilde{\omega}:[0,\infty]\to[0,\infty]$は連続度である:
$$ \tilde{\omega}(\delta):=\sup_{r\in[0,\delta]}\omega(r) \qquad (\delta\in[0,\infty]). $$
また,任意の$\delta\in[0,\infty]$に対して$\omega(\delta)\le\tilde{\omega}(\delta)$が成り立つ.
- $0\le\delta_1\le\delta_2\le\infty$のとき,$[0,\delta_1]\subset[0,\delta_2]$より$\tilde{\omega}(\delta_1)\le\tilde{\omega}(\delta_2)$である.
- $\delta\to +0$のとき$\tilde{\omega}(\delta)\to 0$である.実際,任意の$\varepsilon\in(0,\infty)$に対して「各$r\in[0,\delta]$に対して$\omega(r)\le\varepsilon$が成り立つ」という性質を満たす$\delta\in(0,\infty)$が存在するが,この性質は$\tilde{\omega}(\delta)\le\varepsilon$を意味する.
距離空間の部分集合上で定義された実数値一様連続写像は,(特定の条件下において)その連続度を保ったまま,定義域を距離空間全体へと拡張することができる.
$(X,d_X)$を距離空間,$A$を$X$の空でない部分集合とし,連続度$\omega$は次の2条件を満たすとする.
- $\omega([0,\infty))\subset[0,\infty)$である.
- 任意の$\delta_1,\delta_2\in[0,\infty]$に対して$\omega(\delta_1+\delta_2)\le\omega(\delta_1)+\omega(\delta_2)$が成り立つ(劣加法性).
また,$\omega$-連続な写像$f:A\to\mathbb{R}$に対して写像$f_{\omega},f^{\omega}:X\to\mathbb{R}$を
\begin{align*}
f_{\omega}(x)
&:=\sup_{a\in A}(f(a)-\omega(d_X(x,a))), \\
f^{\omega}(x)
&:=\inf_{a\in A}(f(a)+\omega(d_X(x,a))) \qquad (x\in X)
\end{align*}
で定める.このとき,次のことが成り立つ.
- $f_\omega|_{A}=f^\omega|_{A}=f$である.
- $f_\omega,f^\omega$は$\omega$-連続である.
- 写像$g:X\to\mathbb{R}$が$g|_{A}=f$を満たし,かつ$\omega$-連続ならば,任意の$x\in X$に対して$f_\omega(x)\le g(x)\le f^\omega(x)$である.
$x\in A$を任意に取ると,まず$f_\omega,f^\omega$の定義より
$$ f^\omega(x)\le f(x)+\omega(d_X(x,x))=f(x)=f(x)-\omega(d_X(x,x))\le f_\omega(x), $$
つまり$f^\omega(x)\le f(x)\le f_\omega(x)$を得る.また$f$の$\omega$-連続性より,任意の$a\in A$に対して
$$ f(a)-\omega(d_X(x,a))\le f(x)\le f(a)+\omega(d_X(x,a)) $$
が成り立つから$f_\omega(x)\le f(x)\le f^\omega(x)$を得る.よって$f_\omega(x)=f(x)=f^\omega(x)$が示された.写像の族$\family{g_a^{\pm}:X\to\mathbb{R}}{a\in A}$を次式で定める:
$$ g_a^{\pm}(x):=f(a)\pm\omega(d_X(x,a)) \qquad (a\in A,\ x\in X). $$
このとき$\omega$の劣加法性より,各$g_a^{\pm}$は$\omega$-連続である:実際,任意の$x,x'\in X$に対して
$$ |g_a^{\pm}(x)-g_a^{\pm}(x')|=|\omega(d_X(x,a))-\omega(d_X(x',a))|\le \omega(d_X(x,x')) $$
が成り立つからである.よって,既に示したこと から$\displaystyle f_\omega=\sup_{a\in A}g_a^{-}$と$\displaystyle f^\omega=\inf_{a\in A}g_a^{+}$も$\omega$-連続である.$g$の$\omega$-連続性と$g|_{A}=f$より,任意の$a\in A$に対して
$$ f(a)-\omega(d_X(x,a))=g(a)-\omega(d_X(x,a))\le g(x)\le g(a)+\omega(d_X(x,a))=f(a)+\omega(d_X(x,a)) $$
が成り立つから$f_\omega(x)\le g(x)\le f^\omega(x)$を得る.
上の定理の仮定は,たとえばヘルダー連続写像やリプシッツ連続写像で成り立つから,次の系を得る.
(つまり実数値ヘルダー連続写像は,ヘルダー連続性と"ヘルダー係数"を保ったまま,その定義域を全空間へと拡張できる.)
$(X,d_X)$を距離空間,$A$を$X$の空でない部分集合,$\alpha\in(0,1]$,$L\in(0,\infty)$とし,連続度$\omega$を
$$ \omega(\delta)=L\delta^\alpha \qquad (\delta\in[0,\infty])$$
で定める.このとき,$\omega$-連続な写像$f:A\to\mathbb{R}$に対して写像$f_{\omega},f^{\omega}:X\to\mathbb{R}$を前定理のように
\begin{align*}
f_{\omega}(x)&=\sup_{a\in A}(f(a)-Ld_X(x,a)^\alpha),\\
f^{\omega}(x)&=\inf_{a\in A}(f(a)+Ld_X(x,a)^\alpha) \qquad (x\in X)
\end{align*}
で定めれば,次のことが成り立つ.
- $f_{\omega}|_{A}=f^{\omega}|_{A}=f$である.
- $f_{\omega},f^{\omega}$は$\omega$-連続(特に$\alpha$-ヘルダー連続)である.
- 写像$g:X\to\mathbb{R}$が$g|_{A}=f$を満たし,かつ$\omega$-連続ならば,任意の$x\in X$に対して$f_{\omega}(x)\le g(x)\le f^{\omega}(x)$である.
![リプシッツ連続写像!FORMULA[605][1786189965][0]の,!FORMULA[606][80230590][0]上へのリプシッツ最大拡張!FORMULA[607][1551038891][0](赤い線)・最小拡張!FORMULA[608][1354525386][0](青い線)](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FYaY3dIT2DIwfBRSig2hG.png?alt=media) リプシッツ連続写像$f:[-\pi,\pi]\ni x\mapsto \sin{x}\in\mathbb{R}$の,$\mathbb{R}$上へのリプシッツ最大拡張$f^{\omega}$(赤い線)・最小拡張$f_{\omega}$(青い線)
リプシッツ連続写像$f:[-\pi,\pi]\ni x\mapsto \sin{x}\in\mathbb{R}$の,$\mathbb{R}$上へのリプシッツ最大拡張$f^{\omega}$(赤い線)・最小拡張$f_{\omega}$(青い線)
![!FORMULA[609][-153580035][0]の定義の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FWMukiOLUxbohFHoJa4Qw.gif?alt=media) $f_\omega,f^\omega$の定義の図示
$f_\omega,f^\omega$の定義の図示
また連続度の劣加法性はそれほど強い仮定ではなく,たとえばノルム空間の凸部分集合上で定義された写像の最適連続度は自動的に劣加法性を満たす.
$(V,\|\cdot\|)$をノルム空間,$C$を$V$の凸部分集合,$(Y,d)$を距離空間とし,写像$f:C\to Y$の最適連続度を$\omega_f:[0,\infty]\to[0,\infty]$とする.
このとき,次のことが成り立つ.
- $\delta_1,\delta_2\in[0,\infty]$に対して,$\omega_f(\delta_1+\delta_2)\le\omega_f(\delta_1)+\omega_f(\delta_2)$である.
- $\delta\in[0,\infty)$と$n\in\mathbb{N}$に対して,$\omega_f(n\delta)\le n\omega_f(\delta)$である.
- $\delta,\lambda\in[0,\infty)$に対して,$\omega_f(\lambda\delta)\le(\lfloor\lambda\rfloor+1)\omega_f(\delta)$である.
$\delta_1,\delta_2\in(0,\infty)$の場合のみ考える(そうでない場合は個別に考えれば容易に示せる).
$\|v-v'\|\le\delta_1+\delta_2$を満たす$v,v'\in C$を任意に取る.このとき
$$ v'':=\frac{\delta_2}{\delta_1+\delta_2}v+\frac{\delta_1}{\delta_1+\delta_2}v' $$
とおけば,$v''\in C$かつ$\|v-v''\|\le \delta_1$かつ$\|v''-v'\|\le\delta_2$が成り立つから
\begin{align*} d(f(v),f(v')) &\le d(f(v),f(v''))+d(f(v''),f(v')) \le \omega_f(\delta_1)+\omega_f(\delta_2) \end{align*}
となる.$v,v'$は任意だったから,$\omega_f(\delta_1+\delta_2)\le\omega_f(\delta_1)+\omega_f(\delta_2)$が示された.$\delta\in[0,\infty)$を任意に取り,$n$に関する数学的帰納法で示す.$n=1$の場合は明らか.
ある$n\in\mathbb{N}$について$\omega_f(n\delta)\le n\omega_f(\delta)$が成り立っていたと仮定すると,(1)より
\begin{align*} \omega_f((n+1)\delta) &=\omega_f(n\delta+\delta) \le \omega_f(n\delta)+\omega_f(\delta) \le n\omega_f(\delta)+\omega_f(\delta) =(n+1)\omega_f(\delta) \end{align*}
となる.したがって,任意の$n\in\mathbb{N}$に対して$\omega_f(n\delta)\le n\omega_f(\delta)$であることが示された.$n:=\lfloor\lambda\rfloor$とおくと$n\le\lambda< n+1$だから,(2)より
\begin{align*} \omega_f(\lambda\delta) &\le\omega_f((n+1)\delta) \le (n+1)\omega_f(\delta) = (\lfloor\lambda\rfloor+1)\omega_f(\delta). \end{align*}
連続度の使用例
不等式$d_Y(f(x),f(x'))\le\omega(d_X(x,x'))$等を使うと,$d_X(x,x')$の大きさを一旦気にせずに$d_Y(f(x),f(x'))$に関する評価を先へ進めることができます.
このように連続度を用いて評価した後で$f$の連続性
$$ \lim_{\delta\to +0}\omega(\delta)=0$$
を使えば,$\varepsilon$-$\delta$論法だけを使った煩雑な計算よりもシンプルに議論できて非常に便利です.
いくつか使用例を見てみましょう.
有界閉区間上の連続写像$f:[a,b]\to\mathbb{R}$は$[a,b]$上でリーマン積分可能であることを示せ.
解答例
$[a,b]$の任意の分割
$$ \Delta:{a=x_0< x_1<\cdots< x_{k-1}< x_{k}=b}$$
に対して,$\Delta$に関する$f$の過剰和$S_\Delta$と不足和$s_\Delta$の差は,各小区間$[x_{j},x_{j+1}]$における$f$の最大点と最小点をそれぞれ$x_{\text{max}}^{(j)},x_{\text{min}}^{(j)}$とおけば
\begin{align*}
S_\Delta-s_\Delta
&=\sum_{j=0}^{k-1}{\color{red}(f(x_{\text{max}}^{(j)})-f(x_{\text{min}}^{(j)}))}(x_{j+1}-x_{j}) \\
&\le \sum_{j=0}^{k-1}{\color{red}\omega_{f}(|x_{\text{max}}^{(j)}-x_{\text{min}}^{(j)}|)}(x_{j+1}-x_{j}) \\
&\le \sum_{j=0}^{k-1}\omega_{f}(|\Delta|)(x_{j+1}-x_{j}) \\
&=\omega_{f}(|\Delta|)(b-a)
\end{align*}
と評価できる.ここで,$\omega_f$は$f$の最適連続度とし,$|\Delta|$は分割$\Delta$の幅
$$ |\Delta|:=\max_{j\in\{0,1,\ldots,k-1\}}(x_{j+1}-x_{j}) $$
とした(ここまではどんな分割$\Delta$でも成り立つ議論であることに注意).さて,任意の$\varepsilon\in(0,\infty)$に対して,$f$の一様連続性より
$$ \omega_f(\delta)\le \frac{\varepsilon}{b-a} $$
を満たす$\delta\in(0,\infty)$が取れるから,$|\Delta|<\delta$なる任意の分割$\Delta$に対して$S_\Delta-s_\Delta\le\varepsilon$が成り立つ.したがって,$f$は$[a,b]$上でリーマン積分可能である.
$\Omega$を$\mathbb{R}^n$の可測集合,$f:\Omega\to\mathbb{R}$を可積分写像とし,$g:\mathbb{R}^m\times\Omega\to\mathbb{R}$を有界かつ一様連続な写像とする.
このとき,次式で定める写像$F:\mathbb{R}^m\to\mathbb{R}$
$$ F(x):=\int_{\Omega}f(y)g(x,y)\,dy \qquad (x\in\mathbb{R}^m)$$
は一様連続であることを示せ.
解答例
任意の$x,x'\in\mathbb{R}^m$に対して
\begin{align*}
\abs{F(x)-F(x')}
&= \abs{\int_{\Omega} f(y)g(x,y)\,dy-\int_{\Omega} f(y)g(x',y)\,dy} \\
&\le \int_{\Omega} \abs{f(y)} {\color{red}\abs{g(x,y)-g(x',y)}} \,dy \\
&\le \int_{\Omega} \abs{f(y)} {\color{red}\omega_{g}(\abs{x-x'})} \,dy \\
&= \|f\|_{L^1(\Omega)}\omega_{g}(\abs{x-x'})
\end{align*}
が成り立つから,$F$は$\|f\|_{L^1(\Omega)}\omega_{g}$-連続である.
写像$f:\mathbb{R}^n\to\mathbb{R}$は有界かつ一様連続であるとし,写像の族$\family{K_t:\mathbb{R}^n\to\mathbb{R}}{t\in(0,\infty)}$を
$$ K_t(x):=\frac{1}{(4\pi t)^{n/2}}\exp\bigg({-\frac{|x|^2}{4t}}\bigg) \qquad (t\in(0,\infty),\ x\in\mathbb{R}^n)$$
で定める.このとき,合成積の族$\family{K_t\ast f:\mathbb{R}^n\to\mathbb{R}}{t\in(0,\infty)}$
$$ (K_t\ast f)(x)=\int_{\mathbb{R}^n}K_t(y)f(x-y)\,dy \qquad (t\in(0,\infty),\ x\in\mathbb{R}^n)$$
は$t\to +0$のとき$f$に一様収束することを示せ.
解答例
計算を頑張ると,$\family{K_t}{t\in(0,\infty)}$は次の2性質を満たすことが確かめられる(本題から逸れるため割愛).
- 任意の$t\in(0,\infty)$に対して,$\displaystyle\int_{\mathbb{R}^n}K_t(x)\,dx=1$である.
- 任意の$\delta\in(0,\infty)$に対して,$\displaystyle\lim_{t\to +0}\int_{|x|\ge \delta}K_t(x)\,dx=0$である.
\begin{align*} |(K_t\ast f)(x)-f(x)| &=\bigg|\int_{\mathbb{R}^n}K_t(y)f(x-y)\,dy-f(x)\int_{\mathbb{R}^n}K_t(y)\,dy\bigg| \\ &\le \int_{\mathbb{R}^n}K_t(y){\color{red}|f(x-y)-f(x)|}\,dy \\ &\le \int_{|y|\le\delta}K_t(y){\color{red}\omega_f(|y|)}\,dy+2M\int_{|y|\ge\delta}K_t(y)\,dx \\ &\le \omega_f(\delta)+2M\int_{|y|\ge \delta}K_t(y)\,dy \end{align*}
が成り立つから
$$ \sup_{x\in\mathbb{R}^n}|(K_t\ast f)(x)-f(x)|\le \omega_f(\delta)+2M\int_{|y|\ge \delta}K_t(y)\,dy $$
であり,$t\to +0$の上極限を取ることで
$$ \limsup_{t\to +0}\sup_{x\in\mathbb{R}^n}|(K_t\ast f)(x)-f(x)|\le \omega_f(\delta)+2M\lim_{t\to +0}\int_{|y|\ge \delta}K_t(y)\,dy=\omega_f(\delta) $$
を得る.最後に$\delta\to +0$とすれば,$f$の一様連続性とはさみうちの原理から
$$ \limsup_{t\to +0}\sup_{x\in\mathbb{R}^n}|(K_t\ast f)(x)-f(x)|=0 $$
となり所望の結論が示された.
もし間違い等ありましたら,ご指摘ください.
ここまで読んでいただき,ありがとうございました.
