文献あり

角運動量の合成と球面スピノル

【はじめに】

本記事は角運動量代数の表現と球面調和関数の続きです
本記事はRef.Igiに基づいています

軌道角運動量とスピン

この記事で角運動量の合成に関して述べました。本記事ではそのひとつの重要な応用例を示します。

相対論的な量子力学において、スピン1/2をもつ自由粒子（例えば電子）の波動関数$\psi$は以下のDirac方程式に従います：
\begin{align} \hspace{1.5cm} i\hbar \frac{\partial \psi}{\partial t}=H\psi, \ \ \ H=-i\hbar c{\boldsymbol{\alpha}}\cdot\boldsymbol{\nabla}+mc^2\beta \end{align}
$\hbar,c$は換算プランク定数および光速、$m$は粒子の質量です。$\boldsymbol{\alpha},\beta$は以下の関係を満たします：
\begin{align} \hspace{1.5cm}\{\alpha_i,\alpha_j\}=2\delta_{ij}, \ \ \alpha_i\beta+\beta\alpha_i=0 \ \ \ (i=1,2,3) \end{align}
これを満たす行列には例えば以下のようなものがあります
\begin{align} \hspace{1.5cm} \alpha_i= \begin{pmatrix} 0 & \sigma_i\\ \sigma_i & 0 \end{pmatrix} , \ \ \ \beta= \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \end{align}
ここで$\sigma_i \ (i=1,2,3)$はパウリ行列、$0,1$はそれぞれ2行2列の零行列と単位行列です。

注

上の式が相対論的と言われる所以は、この式がLorentz変換に対して共変だからです。以下簡単にこれを確認します。

この式を書き換えると以下のようになります：
\begin{align} \hspace{1.5cm} &(i\centernot{D}-m)\psi=0,\tag{A} \\ &\centernot{D}:=\gamma^\mu\partial_\mu,\\ &\gamma^0:=\beta, \ \ \ \gamma^i=\beta\alpha_i \ (i=1,2,3)\\ &\text{※ 自然単位系 }\hbar=c=1\text{ を採用している} \end{align}
$\gamma^\mu$は次の反交換関係：$\{\gamma^\mu,\gamma^\nu\}=2g^{\mu\nu}, \ \ \ g^{\mu\nu}=\mathrm{diag}(1,-1,-1,-1)$を満たします（※4x4の単位行列を省略している）。

この形にするとLorentz変換に対する変換性がわかりやすいです。ベクトル量はLorentz変換$\Lambda^\mu{}_\nu$により、スピノルは$S(\Lambda)$によりLorentz変換を受けるとすると
\begin{align} \hspace{1.5cm} x\to x'^\mu=\Lambda^\mu{}_\nu x^\nu, \ \partial_\mu\to\partial'_\mu=\Lambda_\mu{}^\nu \partial_\nu,\ \psi(x)\to \psi'(x')=S(\Lambda)\psi(x) \end{align}
になります。無限小Lorentz変換:$\Lambda^\mu{}_\nu=\delta^\mu{}_\nu+\epsilon^\mu{}_\nu, \ \ |\epsilon^\mu{}_\nu|\ll 1$（$\epsilon^\nu{}_\mu$は反対称）に対し、
\begin{align} \hspace{1.5cm}S\simeq 1-\frac{i}{4}\epsilon_{\mu\nu}\sigma^{\mu\nu},\ \ \ \sigma^{\mu\nu}:=\frac{i}{2}[\gamma^\mu,\gamma^\nu] \end{align}
です。すると
\begin{align} \hspace{1.5cm} \Lambda^\nu{}_\mu S\gamma^\mu S^{-1}= \gamma^\nu+\frac{i}{4}\left\{\gamma^\nu\epsilon_{\alpha\beta}\sigma^{\alpha\beta} -\epsilon_{\alpha\beta}\sigma^{\alpha\beta}\gamma^\nu\right\}+\epsilon^\nu{}_\mu \gamma^\mu+\mathcal{O}(\epsilon^2) \end{align}
となります。ここで
\begin{align} \hspace{1.5cm}A[B,C]=\{A,B\}C-B\{A,C\}-\{A,C\}B+C\{A,B\}+[B,C]A \end{align}
を用いて中括弧内の第1項を書き換えることで
\begin{align} \hspace{1.5cm}\frac{i}{4}\{\gamma^\nu \epsilon_{\alpha\beta}\sigma^{\alpha\beta}-\epsilon_{\alpha\beta}\sigma^{\alpha\beta}\gamma^\nu\}=-\epsilon^\nu{}_\mu\gamma^\mu \end{align}
であることを示せます。ゆえに$\mathcal{O}(\epsilon)$で
\begin{align} \hspace{1.5cm} \Lambda^\nu{}_\mu S\gamma^\mu S^{-1}=\gamma^\nu \tag{B} \end{align}
が成立します。Eq.(A)に左から$S$をかけて
\begin{align} \hspace{1.5cm}S(i\gamma^\mu \partial_\mu-m)\psi(x)=0 \end{align}
とし、$\psi$を$S^{-1}S\psi$として上式に代入してEq.(B)を用いると　
\begin{align} \hspace{1.5cm} &\left[iS\gamma^\mu S^{-1}\partial_\mu -m\right]S\psi(x)=0\\ &\leftrightarrow\left[i\Lambda^\nu{}_\mu S\gamma^\mu S^{-1}\partial'_\nu -m\right]\psi'(x')=0 \ \ \ (\because \partial_\mu=\Lambda^\nu{}_\mu \partial'_\nu \ \ \ (\Lambda\text{は転置で不変}))\\ &\leftrightarrow [i\gamma^\nu\partial'_\nu -m]\psi'(x')=0 \ \ \ (\because \text{Eq.(B)}) \end{align}
を得ます。最後の式はEq.(A)を新たな座標で書いたものになっています。よってEq.(A)はLorentz変換により共変です。${}_\blacksquare$

このハミルトニアンが特徴的なのは、運動項$-i\hbar c\boldsymbol{\alpha}\cdot\boldsymbol{\nabla}= c\boldsymbol{\alpha}\cdot\boldsymbol{p}$が運動量$\boldsymbol{p}$の1次であることです。このために自由粒子でさえ角運動量演算子${\boldsymbol{L}}:=\boldsymbol{x}\times \boldsymbol{p}$（以降これを軌道角運動量と呼ぶ）とハミルトニアンは交換しません：
\begin{align} \hspace{1.5cm}[L_i,H]=i\hbar c({\boldsymbol{\alpha}}\times \boldsymbol p)_i \end{align}
（ちなみに非相対論的な運動エネルギー$\boldsymbol{p}^2/2m$は${\boldsymbol{L}}$と交換します）
一方軌道角運動量とスピンを足した演算子
\begin{align} \hspace{1.5cm} \boldsymbol{J}&=\boldsymbol{L}+\boldsymbol{S},\\ \boldsymbol{S}&:=\frac{\hbar}{2}\boldsymbol{\Sigma},\ \ \ \boldsymbol{\Sigma}:= \begin{pmatrix} \boldsymbol{\sigma} & 0\\ 0 & \boldsymbol{\sigma} \end{pmatrix} \end{align}
は、$[S_i,H]=-i\hbar c({\boldsymbol{\alpha}}\times{\boldsymbol{p}})_i$なので上記の$[L_i,H]$と打消し合うためハミルトニアンと交換します：$[\boldsymbol{J},H]=0$。

この事実は、相対論的な量子力学では軌道角運動量$\boldsymbol{L}$とスピンはそれぞれでは保存せず、それらを足した量が保存されることを示しています。よってハミルトニアンの固有状態はそれらを合成した状態により記述されます。そのため例えば水素原子をDirac方程式を用いて解析すると、そのエネルギー準位は全角運動量（軌道角運動量の大きさとスピンの大きさを足した量）に依存します。

軌道角運動量とスピンの合成

ということで軌道角運動量とスピンを合成します。合成の一般論に関してはRef.Mathlog_02をご参照ください。

スピンとは角運動量の大きさが$1/2$の状態です。よってここから行うことは、角運動量の大きさが$l$（0以上の整数）と$1/2$の状態の合成です。以下$l$は与えられた定数とします。

Ref.Mathlog_02より、次のことがわかります (Ref.Mathlog_02で$j_1\to l, j_2\to 1/2$とする):

全角運動量の大きさ$j$は$l+1/2$から$|l-1/2|=l-1/2$までとります。すなわち
\begin{align} \hspace{1.5cm}j=l+1/2,\ \ \ l-1/2 \end{align}
の2つが可能な$j$です。
$j=l+1/2$において$m$が異なる状態は、この$j$で最も$m$が大きい$|l+1/2,l+1/2\rrangle=|l,l\rangle|1/2,1/2\rangle$の状態に$\hat j^-:=\hat l^-+\hat s^-$を再帰的に作用させることで構成されます。ここで$\hat l^-$は軌道角運動量の下降演算子、$\hat s^-$はスピン角運動量の下降演算子です。$|j,m\rrangle$のように右側が2重カッコになっている記号は合成系の状態を表します。その構成の様子を描いたのが図1です。
$j=j_\text{max}$の状態の構成。$|j_\text{max},j_\text{max}\rrangle$から$\hat j^-$により$m$を減らしていく。
図の$(a,b)$はスピン角運動量の固有状態の$m$が$a$、軌道角運動量の固有状態の$m$が$b$の状態の直積を表します。図の見方の詳細はRef.Mathlog_02をご参照ください。図1より可能な$m$は$m=l+1/2,l-1/2,\cdots,l+1/2-(2l+1)$です。$j_\text{max}:=l+1/2$とすると、$j=j_\text{max}$における各$m$の状態$|j_\text{max},m\rrangle$は

\begin{align} \hspace{1.5cm} &|j_\text{max},m\rrangle=c^{j_\text{max}}_{m+1/2,-1/2}|l,m+1/2\rangle|1/2,-1/2\rangle+ c^{j_\text{max}}_{m-1/2,1/2}|l,m-1/2\rangle|1/2,1/2\rangle,\tag{1}\\ &m=l+1/2,l-1/2,\cdots,l+1/2-(2l+1) \end{align}

と書けることがわかります。$c^{j_\text{max}}_{m+1/2,-1/2}, \ c^{j_\text{max}}_{m-1/2,1/2}$は線形結合の係数です。これらは$|j_\text{max},j_\text{max}\rrangle$から$m$を$\hat j^-$で落とすことによって定まります。

同様に$j=l-1/2$において$m$の最も大きな状態から$\hat j^-$で落とした図が図2です。
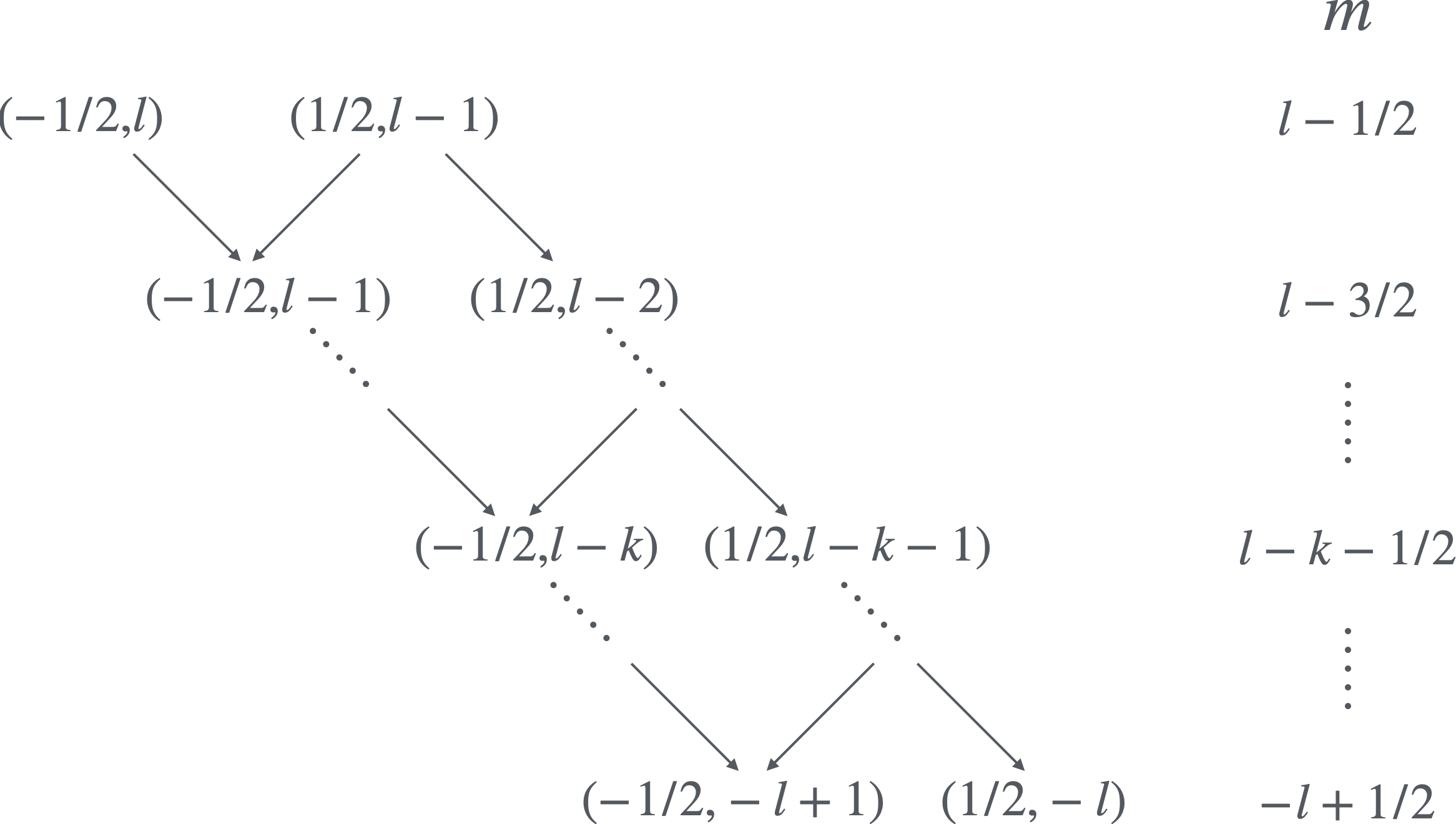画像の名前
図2より、$j=l-1/2$の状態も
\begin{align} \hspace{1.5cm} &|j_\text{max}-1,m\rrangle = c^{j_\text{max}-1}_{m+1/2,-1/2}|l,m+1/2\rangle|1/2,-1/2\rangle+ c^{j_\text{max}-1}_{m-1/2,1/2}|l,m-1/2\rangle|1/2,1/2\rangle,\tag{2}\\ &m=l-1/2,l-3/2,\cdots,l-1/2-(2(l-1)+1) \end{align}
のように書けます。そしてこの場合、Eq.(1)の係数$c^{j_\text{max}}_{m+1/2,-1/2},c^{j_\text{max}}_{m-1/2,1/2}$が求まっていれば、$j=l-1/2$における$c^{j_\text{max}-1}_{m+1/2,-1/2},c^{j_\text{max}-1}_{m-1/2,1/2}$は各$m$におけるEq.(1)とEq.(2)の状態の直交条件および規格化条件からただちに
\begin{align} \hspace{1.5cm} c^{j_\text{max}-1}_{m+1/2,-1/2}=c^{j_\text{max}}_{m-1/2,1/2}, \ \ \ c^{j_\text{max}-1}_{m-1/2,1/2}=-c^{j_\text{max}}_{m+1/2,-1/2} \tag{3} \end{align}
のように求まります（※一意ではありません）。今まで行ってきたように$m$最大の状態から下降演算子で落とす必要はありません。これは$m=l-1/2,\cdots,-l+1/2$における状態がEq.(1)(2)のようにすべて2つの基底で記述されることによります。

係数の決定

$j=l+1/2$における基底の係数（Clebsch-Goradn係数）を定めます。まず以下の公式が成立することに注意します：

\begin{align} \hspace{1.5cm} (\hat l^-)^{j-m}|l,l\rangle= \sqrt{\frac{(2l)!(j-m)!}{(2l-j+m)!}}|l,l-j+m\rangle \end{align}

公式1の証明はここをクリック

$\hat l^-$の$|l,m\rangle$への作用は
\begin{align} \hspace{1.5cm}\hat l^- |l,m\rangle=\sqrt{l(l+1)-m(m-1)}|l,m-1\rangle \end{align}
です。これを繰り返し用いれば以下のように公式1を示せます：
\begin{align} (\hat l^-)^{j-m}|l,l\rangle &= \sqrt{l(l+1)-l(l-1)} \sqrt{l(l+1)-(l-1)(l-2)}\cdots\\ &\hspace{1cm}\times\sqrt{l(l+1)-(l-k)(l-k-1)}\cdots \sqrt{l(l+1)-(l-j+m+1)(l-j+m)} |l,l-j+m\rangle\\ &=\sqrt{2l}\sqrt{4l-2}\cdots\sqrt{(2l-k)(k+1)}\cdots\sqrt{l(l+1)-(l-j+m+1)(l-j+m)} |l,l-j+m\rangle\\ &=\prod_{k=0}^{j-m-1}\sqrt{(2l-k)(k+1)}|l,l-j+m\rangle\\ &=\sqrt{(2l)(2l-1)\cdots(2l-j+m+1)\times 1\cdot 2\cdot \cdots \cdot (j-m)}|l,l-j+m\rangle\\ &=\sqrt{\frac{(2l)!(j-m)!}{(2l-j+m)!}}|l,l-j+m\rangle \ \ \ \ {}_\blacksquare \end{align}

$\hat j^-=\hat l^-+\hat s^-$として、$(\hat j^-)^{j_\text{max}-m}$を$|j_\text{max},j_\text{max}\rrangle=|l,l\rangle|1/2,1/2\rangle$に作用させれば$|j_\text{max},m\rrangle$を得ることができます。公式1で$\hat l^-\to\hat j^-$、$j\to j_\text{max}$、$l\to j_\text{max}$とすれば
\begin{align} \hspace{1.5cm} |j_\text{max},m\rrangle&=\sqrt{\frac{(j_\text{max}+m)!}{(2j_\text{max})!(j_\text{max}-m)!}}(\hat j^-)^{j_\text{max}-m}|j_\text{max},j_\text{max}\rrangle\\ &=\sqrt{\frac{(j_\text{max}+m)!}{(2j_\text{max})!(j_\text{max}-m)!}}(\hat l^-+\hat s^-)^{j_\text{max}-m}|l,l\rangle|1/2,1/2\rangle \end{align}
となります。ここで$\hat s^-$が2回かかるとスピン1/2の状態は消えることを用いると
\begin{align} \hspace{1.5cm} (\hat j^-)^{j_\text{max}-m}=(\hat l^-+\hat s^-)^{j_\text{max}-m} =(\hat l^-)^{j_\text{max}-m}+(j_\text{max}-m)(\hat l^-)^{j_\text{max}-m-1}\hat s^- \end{align}
としてよいです。これと公式1を用いれば以下のようになります：
\begin{align} \hspace{1.5cm} |j_\text{max},m\rrangle &= \sqrt{\frac{(j_\text{max}+m)!}{(2j_\text{max})!(j_\text{max}-m)!}} \{ (\hat l^-)^{j_\text{max}-m}|l,l\rangle|1/2,1/2\rangle +(j_\text{max}-m)(\hat l^-)^{j_\text{max}-m-1}\hat s^-|l,l\rangle|1/2,1/2\rangle \} \\ &=\sqrt{\frac{(j_\text{max}+m)!}{(2j_\text{max})!(j_\text{max}-m)!}} \Bigg\{ \sqrt{\frac{(2l)!(j_\text{max}-m)!}{(2l-j_\text{max}+m)!}}|l,m-1/2\rangle|1/2,1/2\rangle \\ &\hspace{6cm}+(j_\text{max}-m)\sqrt{\frac{(2l)!(j_\text{max}-m-1)!}{(2l-j_\text{max}+m+1)!}}|l,m+1/2\rangle|1/2,-1/2\rangle \Bigg\} \end{align}
$j_\text{max}=l+1/2$を代入し整理すれば
\begin{align} \hspace{1.5cm} |l+1/2,m\rrangle=\sqrt{\frac{l+m+1/2}{2l+1}}|l,m-1/2\rangle|1/2,1/2\rangle +\sqrt{\frac{l-m+1/2}{2l+1}}|l,m+1/2\rangle|1/2,-1/2\rangle \tag{4} \end{align}
を得ます。

$\ket{l-1/2,m}\!\rangle$はEq.(3)からただちに求まります：
\begin{align} \hspace{1.5cm} |l-1/2,m\rrangle=\sqrt{\frac{l-m+1/2}{2l+1}}|l,m-1/2\rangle|1/2,1/2\rangle -\sqrt{\frac{l+m+1/2}{2l+1}}|l,m+1/2\rangle|1/2,-1/2\rangle \end{align}
これはEq.(4)と同じ基底から構成され、直交し、かつ規格化されていることはすぐわかります。

まとめると以下のようになります

軌道角運動量の大きさ$l$とスピン$1/2$の合成

軌道角運動量の大きさが$l$（0以上の整数）およびスピン$1/2$を合成した系の全角運動量$j$は
\begin{align} \hspace{1.5cm} j=l+1/2\text{ と }j=l-1/2 \end{align}
の2つが可能であり、それぞれ状態は以下のようになる。

$j=l+1/2$:
\begin{align} \hspace{1cm} &|l+1/2,m\rrangle=\sqrt{\frac{l+m+1/2}{2l+1}}|l,m-1/2\rangle|1/2,1/2\rangle +\sqrt{\frac{l-m+1/2}{2l+1}}|l,m+1/2\rangle|1/2,-1/2\rangle,\\ &m=l+1/2,l-1/2,\cdots,l+1/2-(2l+1) \end{align}
...計$2l+2$コの状態が存在
$j=l-1/2$:
\begin{align} \hspace{1cm} &|l-1/2,m\rrangle=\sqrt{\frac{l-m+1/2}{2l+1}}|l,m-1/2\rangle|1/2,1/2\rangle -\sqrt{\frac{l+m+1/2}{2l+1}}|l,m+1/2\rangle|1/2,-1/2\rangle,\\ &m=l-1/2,l-3/2,\cdots,l-1/2-(2(l-1)+1) \end{align}
...計$2(l-1)+2$コの状態が存在

球面スピノル

$|l,m\rangle$の状態を極座標表示して球面調和関数（Ref.Mathlog参照のこと）として表し、またスピンの状態を
\begin{align} \hspace{1.5cm} |1/2,1/2\rangle\leftrightarrow \begin{pmatrix}1\\0\end{pmatrix}, \ \ \ \ |1/2,-1/2\rangle \leftrightarrow \begin{pmatrix}0\\1\end{pmatrix} \end{align}
のように2成分ベクトルに対応させます。このようにして角運動量$l$とスピン$1/2$を合成した状態を具体的に表示したものは球面スピノルと呼ばれ、以下のようになります：

球面スピノル

\begin{align} \hspace{1.5cm} {\mathscr{Y}}^{l+1/2,m}(\theta,\varphi) &= \begin{pmatrix} \displaystyle\sqrt{\frac{l+1/2+m}{2l+1}}Y_l^{m-1/2}(\theta,\varphi)\\ \displaystyle\sqrt{\frac{l+1/2-m}{2l+1}}Y_l^{m+1/2}(\theta,\varphi) \end{pmatrix} \\ {} \\ {\mathscr{Y}}^{l-1/2,m}(\theta,\varphi) &= \begin{pmatrix} \displaystyle\sqrt{\frac{l+1/2-m}{2l+1}}Y_l^{m-1/2}(\theta,\varphi)\\ -\displaystyle\sqrt{\frac{l+1/2+m}{2l+1}}Y_l^{m+1/2}(\theta,\varphi) \end{pmatrix} \end{align}
ここで$Y_l^{m\pm 1/2}(\theta,\varphi)$は球面調和関数。Ref.Mathlog参照のこと。

まとめ

本記事では角運動量の合成の重要な応用である、軌道角運動量とスピンの合成に関して述べました。

軌道角運動量の大きさを$l$とすると、スピン1/2の状態と合成することで全角運動量$j$は$j=l+1/2$と$j=l-1/2$の２つの状態をとることが可能です。$j=l+1/2$における最大の$m$の状態$|l+1/2,l+1/2\rrangle$を下降演算子で落としていくことで$j=l+1/2$の全状態を構成することができます。一方$j=l-1/2$の状態は、各$m$で$|j+1/2,m\rrangle$と直交する条件、および規格化条件から定まります。

これらの状態に関し、軌道部分（角度依存性）を極座標を用いて表示し、またでスピンのアップ（$m=1/2$）とダウン（$m=-1/2$）をベクトルの2成分により表したものが球面スピノルです。

最初の章で述べたように、相対論的な量子力学では軌道角運動量とスピンはそれぞれでは保存せず合成したものが保存します。そのため例えばDirac方程式で水素原子の波動関数を求める際、その$\theta,\varphi$依存性およびスピン状態を記述するのに球面スピノルが用いられます。これに関してはそのうち記事にします。

おしまい。${}_\blacksquare$