f(x)/(x+t)の積分2
prpo41,46
前の回
の続きです.前回の最後に,
\begin{align}
\int_0^1\frac{\kappa(1-x)}{\sqrt x}\frac{dx}{1-xt},\int_0^1\kappa(x)\kappa(1-x)\frac{dx}{1-xt}
\end{align}
について触れました.$|x|,|t|\lt1$において,
\begin{align}
\frac{1}{1-xt}=\sum_{n\geq0}x^nt^n
\end{align}
なので,$I\subset(-1,1),|t|\lt1$において,
\begin{align}
\int_If(x)\frac{dx}{1-xt}=F(t)
\end{align}
はmoment$\int_Ix^nf(x)dx$の母関数になっています.
例えば,
\begin{align}
\int_0^1\frac{\kappa(1-x)}{\sqrt x}\frac{dx}{1-xt}=\pi\kappa(t)\Leftrightarrow\int_0^1x^{n-\frac{1}{2}}\kappa(1-x)dx=\pi\beta_n^2
\end{align}
\begin{align}
\int_0^1\kappa(x)\kappa(1-x)\frac{dx}{1-xt}=\frac{\pi}{2}\kappa(t)^2\Leftrightarrow\int_0^1x^{n}\kappa(x)\kappa(1-x)dx=\frac{\pi}{2}\sum_{k=0}^{n}\beta_k^2\beta_{n-k}^2
\end{align}
がわかります.
\begin{align} \int_0^1x^n\ _2F_1\left[\begin{matrix}\frac13,\frac13\\ \frac23 \end{matrix};1-x\right]\frac{dx}{x^{1/3}(1-x)^{1/3}}=\Gamma\left(\frac23\right)^2\frac{\left(\frac23\right)^2_n}{n!^2} \end{align}
これは,
\begin{align}
\int_0^1\frac{_2F_1\left[\begin{matrix}
\frac13,\frac13\\ \frac23
\end{matrix};1-x\right]}{x^{1/3}(1-x)^{1/3}}\frac{dx}{1-xt}=\Gamma\left(\frac23\right)^2\ _2F_1\left[\begin{matrix}\frac23,\frac23\\ 1 \end{matrix};t\right]
\end{align}
と同値です.
この積分は,$\int_0^1\frac{\kappa(1-x)}{\sqrt x}\frac{dx}{1-xt}$の解法と同じ方針で示せます.
偏角を$(-\pi,\pi]$とします.
\begin{eqnarray}
_2F_1\left[\begin{matrix}a,b\\c
\end{matrix};z\right]&:=&\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1t^{b-1}(1-t)^{c-b-1}(1-zt)^{-a}dt\\
\end{eqnarray}
$z\in\mathbb{R},z\in(0,1)$で,
\begin{eqnarray}
_2F_1\left[\begin{matrix}a,b\\c
\end{matrix};\frac{1}{z}\pm0i\right]&=&\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\left(\int_0^z+\int_z^1\right)t^{b-1}(1-t)^{c-b-1}\left(1-\left(\frac{1}{z}\pm0i\right)t\right)^{-a}dt\\
&=&\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\left(\int_0^1z^bt^{b-1}(1-zt)^{c-b-1}(1-t)^{-a}dt+\int_0^1(1-(1-z)t)^{b-1}(1-z)^{c-b}t^{c-b-1}\left(1-\left(\frac{1}{z}\pm0i\right)(1-(1-z)t)\right)^{-a}
dt\right)\\
&=&\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\left(\frac{\Gamma(b)\Gamma(1-a)}{\Gamma(1-a+b)}z^b\ _2F_1\left[\begin{matrix}1+b-c,b\\ 1-a+b\end{matrix};z\right]+e^{\pm a\pi i}z^a(1-z)^{c-b-a}\int_0^1t^{c-b-1}(1-t)^{-a}(1-(1-z)t)^{b-1}dt\right)\\
&=&\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\left(\frac{\Gamma(b)\Gamma(1-a)}{\Gamma(1-a+b)}z^{b}\ _2F_1\left[\begin{matrix}1+b-c,b\\ 1-a+b\end{matrix};z\right]+e^{\pm a\pi i}\frac{\Gamma(1-a)\Gamma(c-b)}{\Gamma(1-a-b+c)}z^a(1-z)^{c-b-a}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-z\right]\right)\\
&=&\frac{\Gamma(c)\Gamma(1-a)}{\Gamma(c-b)\Gamma(1-a+b)}z^b\ _2F_1\left[\begin{matrix}
1+b-c,b\\1-a+b
\end{matrix};z \right]+e^{\pm a\pi i}\frac{\Gamma(1-a)\Gamma(c)}{\Gamma(b)\Gamma(1-a-b+c)}z^a(1-z)^{c-b-a}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-z \right]
\end{eqnarray}
\begin{align}
f(z)=\frac{1}{z-t}\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};z \right]
\end{align}
について次の積分経路$C$で考えます.
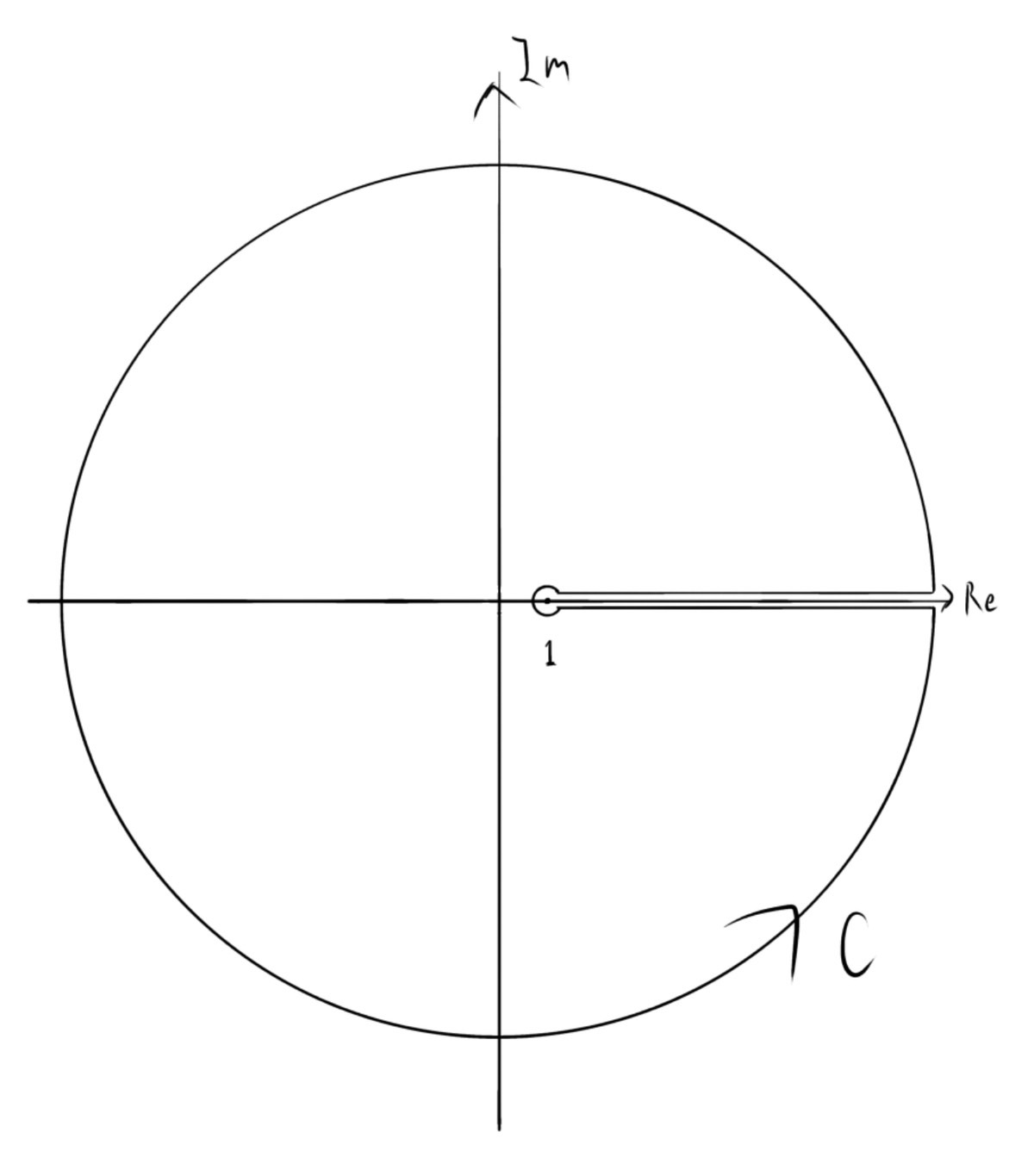
\begin{align}
\oint_Cf(z)dz=\int_1^{\infty}f(x+0i)-f(x-0i)dx+\int_{-\pi}^{\pi}f(\infty e^{ix})\infty ie^{ix}dx-\int_{-\pi}^{\pi}f(1+0e^{ix})0ie^{ix}dx
\end{align}
であり,$a\gt0$で
\begin{align}
\lim_{R\to\infty}\int_{-\pi}^{\pi}\frac{i}{1-\frac{t}{Re^{ix}}}\frac{\Gamma(c)}{\Gamma(b)\Gamma(c-b)}\int_0^1y^{b-1}(1-y)^{c-b-1}(1-Re^{ix}y)^{-a}dydx\to0
\end{align}
また,$|z|\lt1,c-a-b\notin\mathbb{Z}$で
\begin{align}
_2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};1-z \right]=\frac{\Gamma(c)\Gamma(c-a-b)}{\Gamma(c-a)\Gamma(c-b)}\ _2F_1\left[\begin{matrix}
a,b\\a+b-c+1
\end{matrix};z \right]+\frac{\Gamma(c)\Gamma(a+b-c)}{\Gamma(a)\Gamma(b)}z^{c-a-b}\ _2F_1\left[\begin{matrix}
c-a,c-b\\c-a-b+1
\end{matrix};z \right]
\end{align}
なので,$c-a-b\notin\mathbb{Z}$で
\begin{align}
\lim_{\varepsilon\to0}\int_{-\pi}^{\pi}\frac{i\varepsilon e^{ix}}{\varepsilon e^{ix}-t}\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};1+\varepsilon e^{ix} \right]dx\to0
\end{align}
が容易にわかります.
$c-a-b=0$のとき,
\begin{align}
_2F_1\left[\begin{matrix}
a,b\\a+b
\end{matrix};1-z \right]=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\left(\ln\frac1z\ _2F_1\left[\begin{matrix}
a,b\\1
\end{matrix};z \right]+\sum_{n\geq0}\frac{(a,b)_n}{n!^2}z^n\left(2\psi(1+n)-\psi(a+n)-\psi(b+n)\right)\right)
\end{align}
だそうで,これでも
\begin{align}
\lim_{\varepsilon\to0}\int_{-\pi}^{\pi}f(1+\varepsilon e^{ix})\varepsilon ie^{ix}dx\to0
\end{align}
です.
このとき,
\begin{eqnarray}
\oint_Cf(z)dz&=&\int_1^{\infty}f(x+0i)-f(x-0i)dx
&=&2\pi i\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};t \right]
\end{eqnarray}
であり,
\begin{eqnarray}
\int_1^{\infty}f(x+0i)-f(x-0i)dx&=&\frac{\Gamma(1-a)\Gamma(c)}{\Gamma(b)\Gamma(1-a-b+c)}\int_1^{\infty}2i\sin(a\pi)x^{-a}\left(1-\frac{1}{x}\right)^{c-a-b}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-\frac{1}{x} \right]\frac{dx}{x-t}\\
&=&2i\sin(a\pi)\frac{\Gamma(1-a)\Gamma(c)}{\Gamma(b)\Gamma(1-a-b+c)}\int_0^1\frac{x^{a-1}(1-x)^{c-a-b}}{1-xt}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-x \right]dx
\end{eqnarray}
以上より,
\begin{align}
\int_0^1\frac{x^{a-1}(1-x)^{c-a-b}}{1-xt}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-x \right]dx=\frac{\pi}{\sin(a\pi)}\frac{\Gamma(b)\Gamma(1-a-b+c)}{\Gamma(c)\Gamma(1-a)}\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};t \right]
\end{align}
です.
$a=b=\frac23,c=1$とすれば,
\begin{align}
\int_0^1\frac{x^{-1/3}(1-x)^{-1/3}}{1-xt}\ _2F_1\left[\begin{matrix}
\frac13,\frac13\\\frac23
\end{matrix};1-x \right]dx=\Gamma\left(\frac{2}{3}\right)^3\ _2F_1\left[\begin{matrix}
\frac13,\frac13\\1
\end{matrix};t \right]
\end{align}
がわかります.
この方法では二つの超幾何級数の積に関する積分は,
\begin{align}
\int_0^1x^{a-b-1}(1-x)^{c-a-b}\left(\ _2F_1\left[\begin{matrix}
1+b-c,b\\1-a+b
\end{matrix};x \right]\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-x \right]+\cos(a\pi)\frac{\Gamma(c-b)\Gamma(1-a+b)}{\Gamma(b)\Gamma(1-a-b+c)}x^{a-b}(1-x)^{c-b-a}\ _2F_1\left[\begin{matrix}
1-b,c-b\\1-a-b+c
\end{matrix};1-x \right]^2\right)\frac{dx}{1-xt}\\
=\frac{\pi}{2\sin(a\pi)}\frac{\Gamma(b)\Gamma(c-b)\Gamma(1-a+b)\Gamma(1-a-b+c)}{\Gamma(1-a)^2\Gamma(c)^2}\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};t \right]^2
\end{align}
となりそうです.
MrMathsterさんから
Meijir-G function
)を用いた
解法
が挙げられました.このMeijier-G functionは
Mellin-Barnes integral
の一般化になっているものだと思いますが,ここから上の式は得られるのでしょうか.
\begin{align} \int_0^1\frac{\kappa(x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}=\frac{\pi\kappa(1-t)}{t\kappa(t)}-\frac{4\ln2-\ln\frac{t}{1-t}}{t} \end{align}
これも$\frac{1}{x+t}$を含む積分となっています.
\begin{eqnarray}
\int_0^1\frac{\kappa(x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}&=&\int_0^1\left(1-\frac{\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\right)\frac{dx}{1-xt}\\
&=&-\frac{\ln(1-t)}{t}-\int_0^1\frac{\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}\\
\end{eqnarray}
なので,
\begin{align}
\int_0^1\frac{\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}=\frac{4\ln2-\ln t}{t}-\frac{\pi\kappa(1-t)}{t\kappa(t)}
\end{align}
と同値です.
この積分は
$K^2+K'^2$を分母にもつ関数の定積分
にあるものです.
\begin{align}
f(z)=\frac{\kappa(1-z)}{\kappa(z)}\frac{1}{z(z-t)}
\end{align}
の複素積分を考えます.偏角を$(-\pi,\pi]$としたとき,
$\kappa(z)$は$z\in(1,\infty)$で正則でないので,$f(z)$は$z\in(-\infty,0)$と$z\in(1,\infty)$で正則でないです.
そのため次のような積分経路で複素積分を考えます.
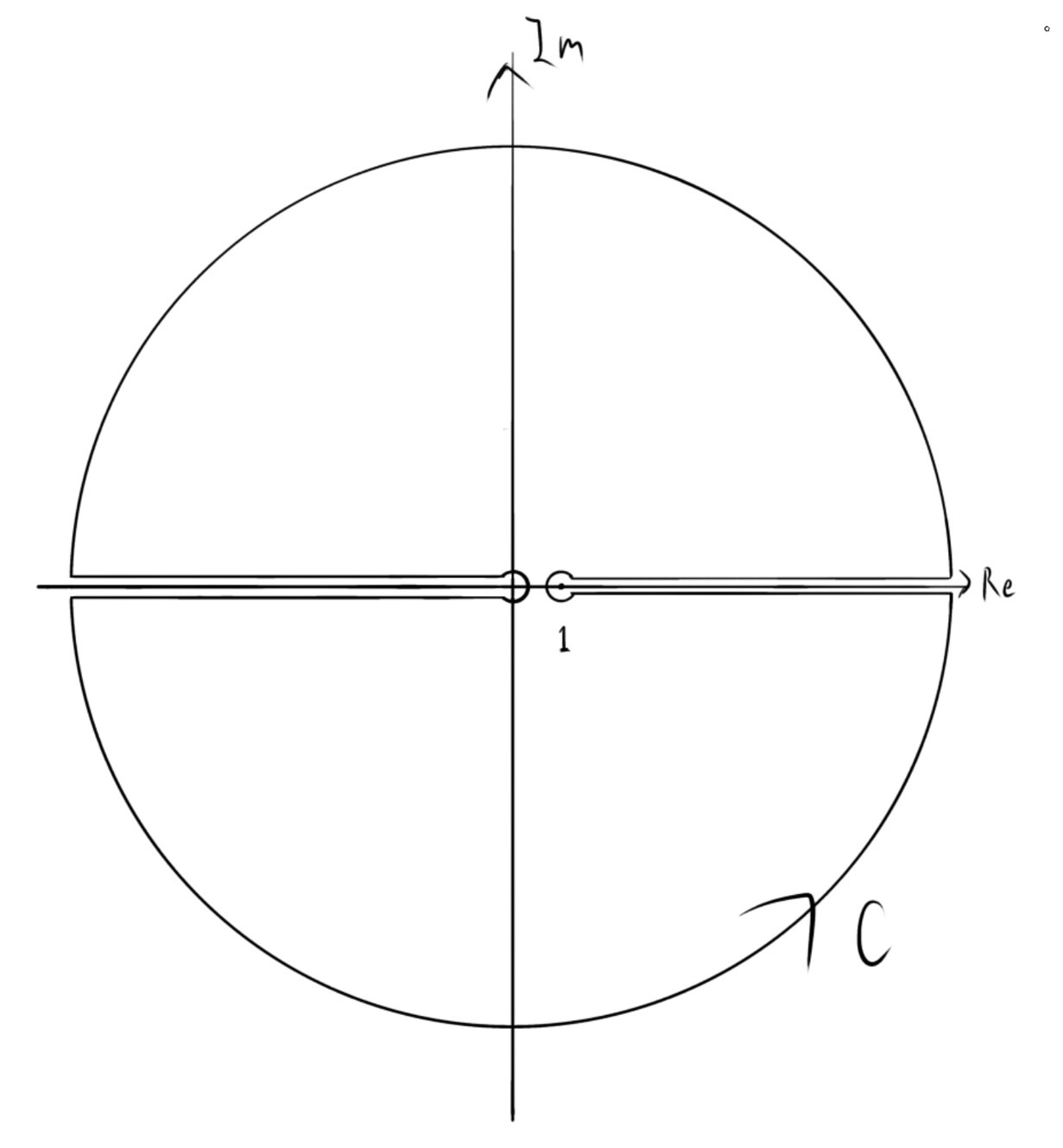
$R\to\infty,\varepsilon\to0$で
\begin{align}
\oint_Cf(z)dz=\int_1^{R}f(x+0i)-f(x-0i)dx+\int_{-R}^{-\varepsilon}f(x+0i)-f(x-0i)dx+\int_{-\pi}^{\pi}f(Re^{ix})Rie^{ix}dx-\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx-\int_{-\pi}^{\pi}f(1+\varepsilon e^{ix})\varepsilon ie^{ix}dx
\end{align}
となります.また,経路内は$z=t$以外で正則なので,留数定理より,
\begin{align}
\oint_Cf(z)dz=2\pi i\frac{\kappa(1-t)}{t\kappa(t)}
\end{align}
です.
\begin{align}
\int_{-\pi}^{\pi}f(Re^{ix})Re^{ix}dx=\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon e^{ix}dx\to0
\end{align}
\begin{eqnarray} \int_{-\pi}^{\pi}\frac{\kappa(1-Re^{ix})}{\kappa(Re^{ix})}\frac{dx}{Re^{ix}-t}&=&\int_{-\pi}^{\pi}\frac{\int_0^1\frac{du}{\sqrt{u(1-u)(1-(1-Re^{ix})u)}}}{\int_0^1\frac{du}{\sqrt{u(1-u)(1-Re^{ix}u)}}}\frac{dx}{Re^{ix}-t}\\ &=&\int_{-\pi}^{\pi}\frac{\int_0^1\frac{du}{\sqrt{u(1-u)(e^{ix}u+\frac{1-u}{R})}}}{\int_0^1\frac{du}{\sqrt{u(1-u)(-e^{ix}u+\frac{1}{R})}}}\frac{dx}{Re^{ix}-t}\\ &\overset{R\to\infty}{=}&0 \end{eqnarray}
\begin{eqnarray} \int_{-\pi}^{\pi}f(1+\varepsilon e^{ix})\varepsilon e^{ix}dx&=&\int_{-\pi}^{\pi}\frac{\kappa(-\varepsilon e^{ix})}{\kappa(1+\varepsilon e^{ix})}\frac{dx}{\varepsilon e^{ix}-t}\\ &\overset{\varepsilon\to0}{=}&0\ \left(\because\kappa(1+\varepsilon e^{ix})\approx-\frac{1}{\pi}\ln\varepsilon\right) \end{eqnarray}
と,
\begin{eqnarray} \int_1^{\infty}f(x+0i)-f(x-0i)dx&=&\int_1^{\infty}\left(\frac{\sqrt{x}}{\kappa(\frac1x)+i\kappa(1-\frac1x)}-\frac{\sqrt x}{\kappa(\frac1x)-i\kappa(1-\frac1x)}\right)\frac{\kappa(1-x)}{x(x-t)}dx\\ &=&\int_1^{\infty}\frac{-2i\kappa(1-\frac{1}{x})}{\kappa(\frac{1}{x})^2+\kappa(1-\frac{1}{x})^2}\frac{\sqrt{x}\kappa(1-x)}{x(x-t)}dx\\ &=&\int_0^1\frac{-2i\kappa(1-x)}{\kappa(x)^2+\kappa(1-x)^2}\frac{\frac{1}{\sqrt{x}}\kappa(1-\frac{1}{x})}{1-xt}dx\\ &=&\int_0^1\frac{-2i\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt} \end{eqnarray}
(途中$\kappa(\frac{x-1}{x})=\sqrt{x}\kappa(1-x)$を用いました.)
$x\in(0,1)$で
\begin{eqnarray} \kappa\left(1-\frac1x\right)&=&\frac{1}{\pi}\int_0^1\frac{dt}{\sqrt{t(1-t)(1-(1-\frac1x)t)}}\\ &=&\frac1\pi\int_0^1\frac{dt}{\sqrt{(1-t)t(1-(1-\frac1x)(1-t))}}\\ &=&\frac{1}{\pi}\int_0^1\frac{\sqrt{x}}{\sqrt{(1-t)t(1-(1-x)t)}}dt\\ &=&\sqrt{x}\kappa(1-x) \end{eqnarray}
なので,
\begin{eqnarray} \oint_Cf(z)dz=2\pi i\frac{\kappa(1-t)}{t\kappa(t)}\\ \Leftrightarrow\int_0^1\frac{\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}&=&-\pi \frac{\kappa(1-t)}{t\kappa(t)}+\lim_{\varepsilon\to0}\frac{1}{2i}\left(\int_{-\infty}^{-\varepsilon}f(x+0i)-f(x-0i)dx-\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx\right) \end{eqnarray}
となります.
$x\in(1,\infty)$で,
\begin{align} \kappa(x\pm0i)=\frac{1}{\sqrt x}\left(\kappa\left(\frac{1}{x}\right)\pm i\kappa\left(1-\frac1x\right)\right) \end{align}
なので,$x\in(-\infty,0)$で,
\begin{align} \kappa(1-x\pm0i)=\frac{1}{\sqrt{1-x}}\left(\kappa\left(\frac{1}{1-x}\right)\pm i\kappa\left(1-\frac{1}{1-x}\right)\right) \end{align}
なので,
\begin{eqnarray} \int_{-\infty}^{-\varepsilon}f(x+0i)-f(x-0i)dx&=&\int_{-\infty}^{-\varepsilon}\left(\frac{1}{\sqrt {1-x}}\left(\kappa\left(\frac{1}{1-x}\right)-i\kappa\left(1-\frac{1}{1-x}\right)\right)-\frac{1}{\sqrt{1-x}}\left(\kappa\left(\frac{1}{1-x}\right)+i\kappa\left(1-\frac{1}{1-x}\right)\right)\right)\frac{dx}{\kappa(x)x(x-t)}\\ &=&\int_{-\infty}^{-\varepsilon}\frac{-2i\kappa(1-\frac1{1-x})}{\sqrt{1-x}\kappa(x)}\frac{dx}{x(x-t)}\\ &=&\int_{-\infty}^{-\varepsilon}\frac{-2i}{x(x-t)}dx\\ &=&\int_{\varepsilon}^{\infty}\frac{-2i}{x(x+t)}dx\\ &=&-\frac{2i}{t}\left[\ln\frac{x}{x+t}\right]_{\varepsilon}^{\infty}\\ &=&\frac{2i}{t}\left(\ln\varepsilon-\ln(t+\varepsilon)\right) \end{eqnarray}
となります.
次に,$|z|\lt1$で
\begin{align} \frac{\kappa(1-z)}{\kappa(z)}=\frac{4\ln2-\ln z}{\pi}-\frac{z}{2\pi}+O(z^2) \end{align}
なので,
\begin{eqnarray} \int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx&=& \int_{-\pi}^{\pi}\frac{\kappa(1-\varepsilon e^{ix})}{\kappa(\varepsilon e^{ix})}\frac{i}{\varepsilon e^{ix}-t}dx\\ &=&\int_{-\pi}^{\pi}\left(\frac{4\ln-\ln\varepsilon-ix}{\pi}+O(\varepsilon)\right)\left(-\frac{1}{t}-\frac{\varepsilon e^{ix}}{t^2}+O(\varepsilon^2)\right)idx\\ &=&-2i\frac{4\ln2-\ln\varepsilon}{t} \end{eqnarray}
となります.($\int_{-\pi}^{\pi}e^{nix}dx=\int_{-\pi}^{\pi}xdx=0\ (n\in\mathbb{Z}_{\ne0})$より$O(\varepsilon)$等が消える.)
故に,
\begin{eqnarray} \lim_{\varepsilon\to0}\left(\int_{-\infty}^{-\varepsilon}f(x+0i)-f(x-0i)dx-\int_{-\pi}^{\pi}f(\varepsilon e^{ix})\varepsilon ie^{ix}dx\right)&=&\lim_{\varepsilon\to0}\left(\frac{2i}{t}(\ln\varepsilon-\ln(\varepsilon+t))+2i\frac{4\ln2-\ln\varepsilon}{t}\right)\\ &=&2i\frac{4\ln2-\ln t}{t} \end{eqnarray}
以上より,
\begin{align} \int_0^1\frac{\kappa(1-x)^2}{\kappa(x)^2+\kappa(1-x)^2}\frac{dx}{1-xt}=\frac{4\ln2-\ln t}{t}-\frac{\pi\kappa(1-t)}{t\kappa(t)} \end{align}
となります.
f(x)/(x+t)の積分
prop46に関しては,
\begin{eqnarray}
\int_0^1x^{s-1}(1-x)^{t-1}\ _2F_1\left[\begin{matrix}
a,b\\c
\end{matrix};1-x \right]dx&=&\frac{\Gamma(s)\Gamma(t)}{\Gamma(s+t)}\ _3F_2\left[\begin{matrix}
a,b,s\\c,s+t
\end{matrix};1 \right]
\end{eqnarray}
なので,先ほどの結果は$s=c$というだけの結果になっています.
つまり,右辺が$_2F_1[...;1]$になり容易に計算可能になっているわけです.
$_3F_2[...;1]$が計算できる定理として,Dixon,Watson,Whipple,Saalschutzの定理がありますが,それらにつながるような結果ではなかったです.
上のような超幾何級数を含む積分で次の積分らが知られています.
\begin{align}
P_v(x):=\ _2F_1\left[\begin{matrix}
-v,v+1\\1
\end{matrix};\frac{1-x}{2} \right],Q_v(x):=\frac{\pi}{2\sin(\pi v)}(P_v(x)\cos(\pi v)-P_v(-x))
\end{align}
\begin{eqnarray}
p.v.\frac12\int_{-1}^1(1+z)^{v-n}P_v(z)\frac{dz}{x-z}&=&
(1+x)^{v-n}Q_v(x)\ \left(n\in\mathbb{Z}_{\geq0},\mathrm{Re}(v-n)\gt-1,-1\lt x\lt1\right)\\
p.v.\int_{-1}^{1}\frac{P_v(z)P_v(-z)}{x-z}dz&=&\frac{\pi}{2\sin(\pi v)}\left(P_{v}(x)^2-P_v(-x)^2\right)\ (v\in\mathbb{C\setminus Z},-1\lt x\lt1)
\end{eqnarray}
$P_v(x)$はルジャンドル多項式$P_n(x)$の$n$を実数に拡張したものになっていると思います.
$v=-\frac12$なら,$P_{-\frac12}(x)=\kappa(\frac{1-x}{2}),Q_{-\frac{1}{2}}(x)=\kappa(\frac{1+x}{2})$となります.
これらは次の論文で挙げられているものです.
(これは前々回の記事の[1]論文です.)
この論文では$P_v,P_v^2$等が満たす微分方程式から,
\begin{align}
T_{n,v}:=\int_{-1}^{1}P_{n}(x)P_{v}(x)P_{v}(-x)dx
\end{align}
の満たす漸化式を得たり,上に挙げた有限ヒルベルト変換から,
\begin{align}
\int_{-1}^{1}xP_v(x)^3P_v(-x)dx=\frac{\sin(2\pi v)\cos(\pi v)}{(2v+1)^2\pi}\ \left(v\in\mathbb{C}\right)
\end{align}
($v=-\frac12$は極限を取る)などを求めたり,
\begin{align}
\int_0^1K'(x)^3dx=\frac{10}{3}\int_0^1K(x)^3dx=5\int_0^1xK(x)^3dx=3\int_0^1K(x)^2K'(x)dx=2\int_0^1K(x)K'(x)^2dx=6\int_0^1xK(x)^2K'(x)dx=\frac{\Gamma(\frac14)^8}{128\pi^2}
\end{align}
を示したりしています.
