1点を除いて定数関数な関数で学ぶ位相空間
どうも
こんにちは ごててんです 社会人も2年目に突入し、いよいよ数学もかなり忘れました(泣)
この記事は、位相空間を少し学んだくらいの人向けの記事です! やさしい記事にする予定ですので、位相空間の定義を知ったくらいの人もどうぞ! 位相空間の色々な分野をつまみ食いする記事になります!!!
あ、イプシロンデルタくらいは使える想定の記事です
本題?
今回は「1点を除いて定数関数な関数が連続でない」ことを証明していこうと思います。
そんなの簡単だ!と思われるかもしれませんが、簡単です。ですが証明の記事を書いていこうと思います。よろしくお願いします。
主張
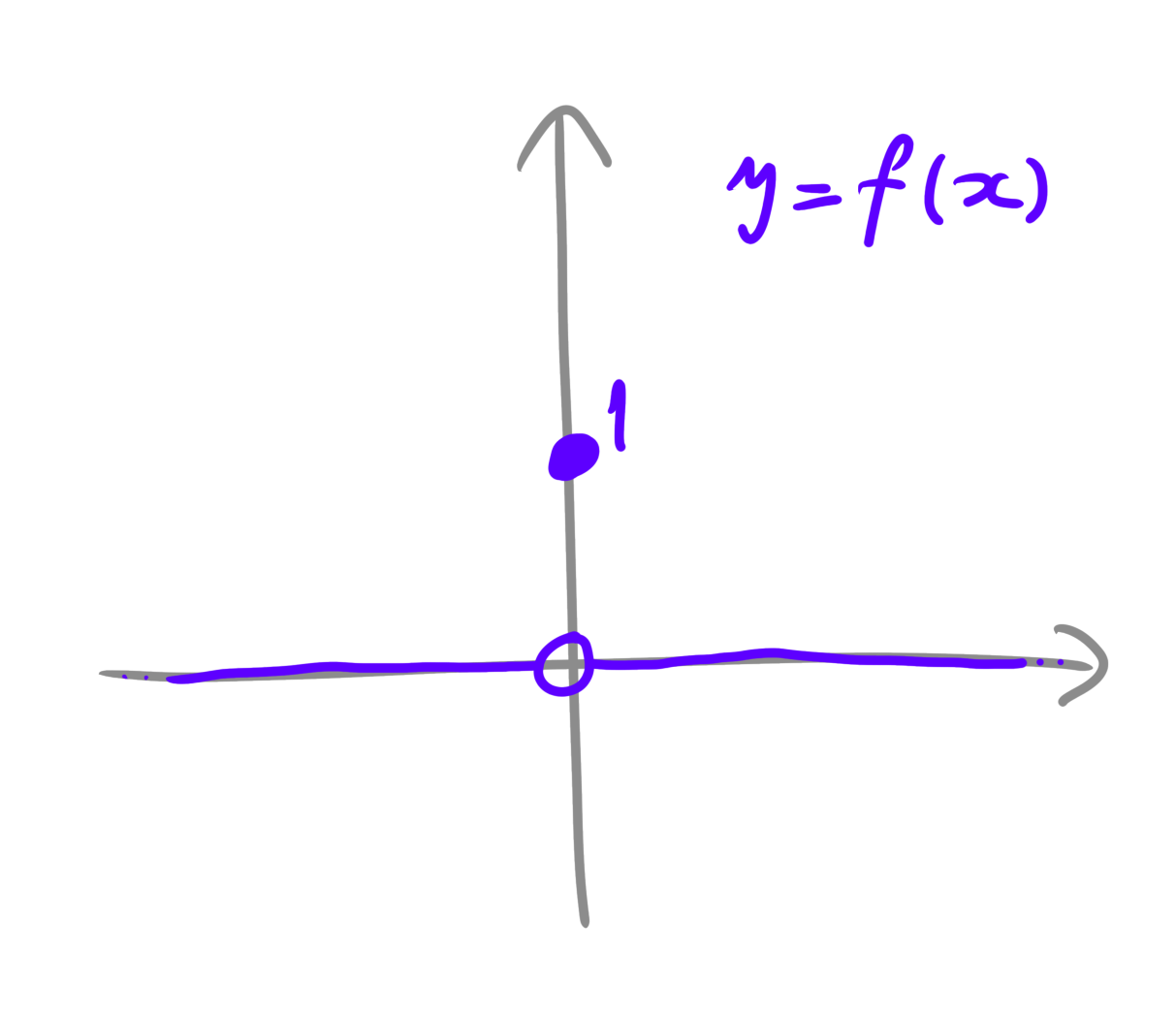
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
$x=0$でだけ$1$, それ以外は$0$をとる関数です。絶対に連続関数ではなさそうですね。
 iPadとペンシル買いました
iPadとペンシル買いました
解き方
さて、この関数が連続関数でないことを示していきましょう!
連続であることの定義からそのままやっていきます。$x=0$の点で連続でないことを示します。
(や、やばい!スッとイプシロンデルタを書けなくなってる!!!)
証明すればいいのは、「$\epsilon > 0$が存在して、任意の$\delta>0$について $0<|x-0|<\delta$となる$x$が存在して$|f(x)-f(0)| \ge \epsilon$」です。連続の否定ってなんか、いつ見ても不安になりますね(合ってるか本当に不安です)(合ってますよね......?)
式を整理すると、「$\epsilon > 0$が存在して、任意の$\delta>0$について $0<|x|<\delta$となる$x$が存在して$|1-0| = 1 \ge \epsilon$」ですね。はい。 $0<\epsilon \le 1$となる実数を何かひとつ出せれば終わりです。う~~~~~~~~~~ん $\pi/4$ がありますね。証明終わり!!!
いや、待て
この回答は頭を使いすぎです。ここは Mathlog ですし、せっかくなので少々、奇を衒いましょう。この問題を位相空間で考えてみます。
位相空間編
基礎知識?
位相空間の勉強をしていると「連続写像」の概念にたどり着くと思います。それと今回扱う実連続関数との関連を一応述べておきます。実連続関数とは、値域が$\mathbb{R}$(通常の位相です)の連続写像のことを指します。定義域が$\mathbb{R}$で、こちらも通常の位相を考えている場合には、解析学における連続関数と一致します。
位相空間の場合の連続写像を一応定義しておきましょう。(今回使うものだけ書いておきます)
$(X,\mathcal{O}_X), (Y,\mathcal{O}_Y)$を位相空間, $f:X \rightarrow Y$を写像とするとき, $f$が連続写像であるとは次が成立することである. (実際には同値であるので, どれか一つが成立していればよい.)
- $Y$の任意の開集合$O$に対して, その逆像$f^{-1}(O)$も開集合.
- $X$の任意の部分集合$A$に対して, つねに$f( \overline{A} ) \subset \overline{f(A)}$が成立する. ($\overline{A}$は$A$の閉包を指す.)
解き方2
じゃあ、やってみましょう。上の定義の(1)を使ってみます。問題文をもう一度貼っておきます。
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
怪しい部分を小突いていきましょう。開区間$I=(1/2,3/2)$を考えてその逆像を取ると、$f^{-1}(I) = \{0\}$で、これは開集合ではありません。よって、$f$は連続ではありません!簡単ですね~
解き方3
では(2)の方も使ってみましょう。$A= \mathbb{R} - \{0\}$とすると, $\overline{A} = \mathbb{R},$ $f(\overline{A})=\{0,1\},$ $ f(A)=\{0\},$$\overline{f(A)} = \{0\}$です。よって、$f( \overline{A} ) \not \subset \overline{f(A)}$なので、連続ではありません。
点列連続性を見てみよう
点列について解説を書いておこうと思います。まあ正直読み飛ばしてもいいですが、少し頑張って書いたことだけは主張しておきます(チラ)
位相空間でも点列の収束を定義できます。定義は次のようになります。
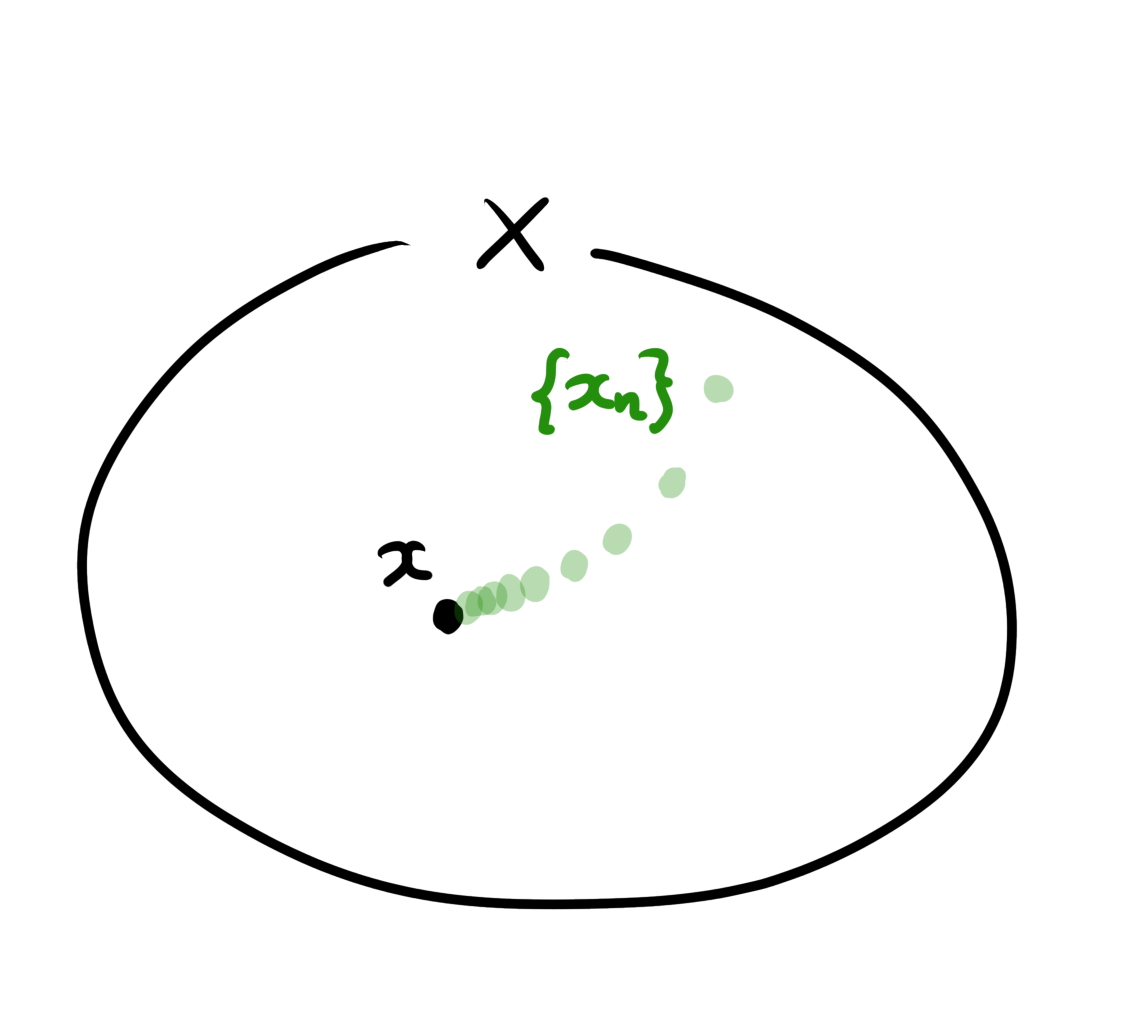
$(X,\mathcal{O})$を位相空間とする. 点列$\{x_n\}_{n\in\mathbb{N}}$が点$x \in X$に収束する($x$が点列の極限値)とは, 次を満たすことである.
・任意の点$x$の近傍$N \subset X$に対し$n_0 \in \mathbb{N}$が存在して, $n > n_0$となる任意の$n \in \mathbb{N}$について$x_n \in N$が成立する.
 記事は適度に空白と挿絵がある方が読みやすい
記事は適度に空白と挿絵がある方が読みやすい
点列が与えられて、そこに極限が存在するとしても、それが一意とは限りません!
ハウスドルフ空間なら収束先は一つです。
収束先が一意でない例も出しておきましょう。(ここは読み飛ばしても大丈夫です)
$X$を元の数が$2$以上の集合、そして密着位相が入っているとしましょう。すると、任意の点列は任意の点に収束します。一応説明を書いておきます。
$\{x_n\}$を点列, $x$を$X$の点とします。さて、密着位相において、近傍となりうる集合は全体集合しかありえません。なぜなら近傍は何か空でない開集合を含んでいなければなりませんが、密着位相において空でない開集合は全体集合のみであるからです。これを念頭において収束の条件を一睨すると、任意の点列が任意の点に収束することがわかると思います。
離散位相や密着位相についてイメージが湧いていない場合はこの記事( 離散位相の「離散」ってなんだよ!!!!!!!!!!!!!!! )をチェックしてみましょう!!!!!!!!!!!!!!!(我田引水)
さて、この記事のメインテーマは連続関数です。関連して点列連続性について述べておきます。
$(X,\mathcal{O}_X), (Y,\mathcal{O}_Y)$を位相空間, $f:X \rightarrow Y$を写像, $x \in X$とする. 写像$f$が点$x$において点列連続であるとは, 次を満たすことである.
・点$x$に収束するどんな$X$の点列$\{x_n\}$に対しても, $Y$の点列$\{f(x_n)\}$がつねに$f(x)$に収束する.
 杜撰な図3
杜撰な図3
そしてこれについて、次の命題が成り立ちます。
$(X,\mathcal{O}_X), (Y,\mathcal{O}_Y)$を位相空間, $f:X \rightarrow Y$を写像とする.
このとき, 写像$f$が点$x \in X$で連続なら, $f$は点$x$で点列連続.
(写像の、各点ごとの連続性についてこの記事では定義していませんが、まあここを読んでる人は知ってるでしょうしいいかなと思って省きました。書くのが面倒だったわけではありません)
さて、初等的な解析学を勉強した皆さんは、この逆が成り立つか気になるかもしれません。この逆ですが、必ず成立するというわけではありません!位相空間$(X,\mathcal{O}_X)$が第1可算公理を満たしている必要があります。興味が出ましたら調べてみてください!私の記事もありますよ!!!
 第1可算公理を点列わいわい公理と呼びたい
第1可算公理を点列わいわい公理と呼びたい
あ、あと点列に興味が出た!という場合はですね、よりうまく位相空間の収束を扱える概念として「フィルター」がありますので ネットで位相空間におけるフィルターについて調べてみましょう!
解き方4
いや、点列連続の説明でつかれた...... ではようやく運用の段階です
まあ、あの、お気づきの方はいると思うのですが点列連続の説明をする必要って全く無かったんですよね 実数関数の場合って別に 初等的な解析学としてみなさんすでに学んでいると思いますし 説明したかったので書きました(てへ)
問題文をもう一度貼っておきます。
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
では解き方4です。
点列$\{x_n\}_{n>0}$を$x_n = 1/n$で定義するとこれは$0$に収束します。そして、$\{f(x_n)\}_{n>0}=\{0\}_{n>0}$は$0 \ne f(0)$に収束します。
よって$f$は$0$において点列連続でないので、連続ではありません!
連結性
まだ行きますよ!次は連結性の話です。
位相空間は幾何学を考えているので、空間が繋がっているとかそういうのも扱いたいわけです。
早速、連結性を定義します。
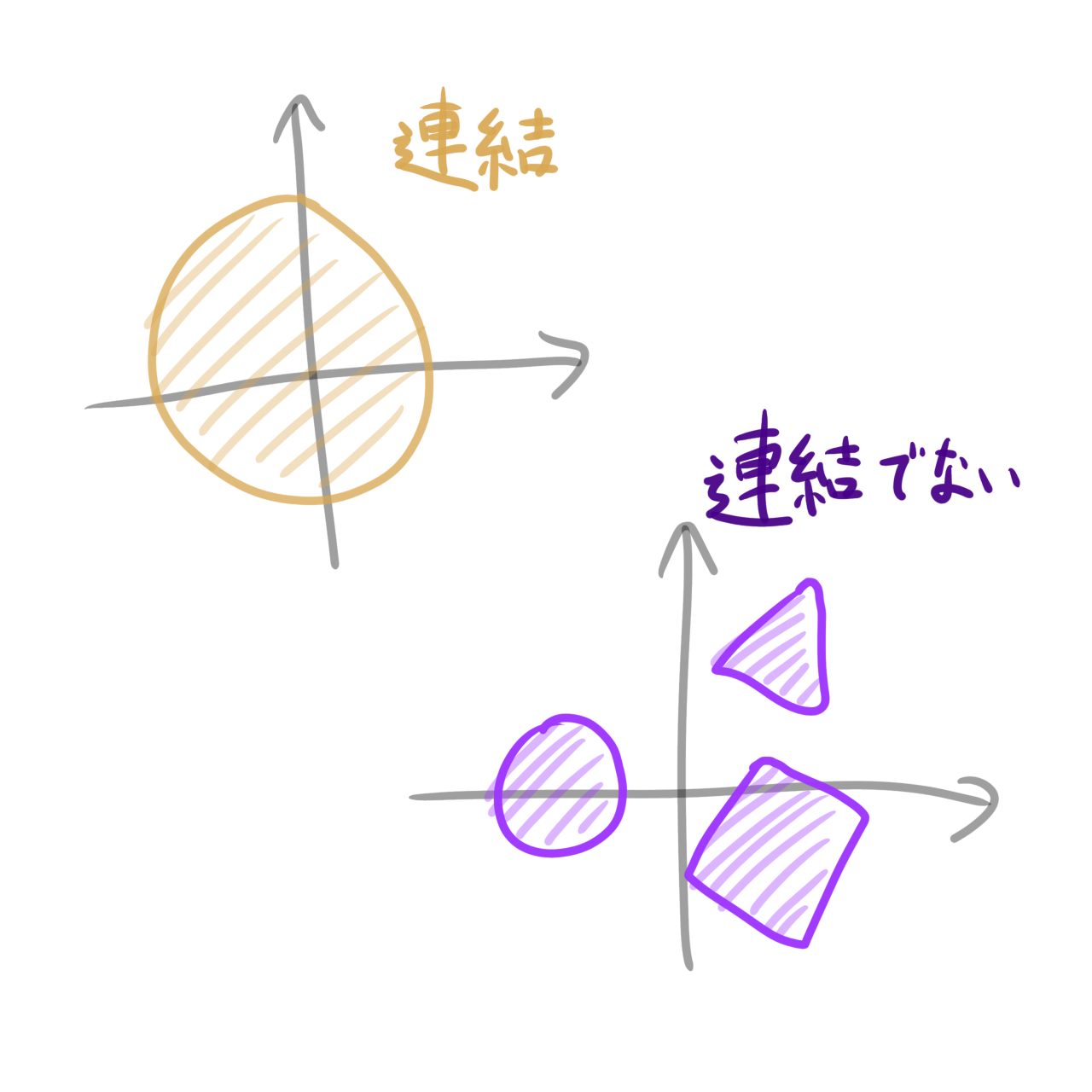
$(X,\mathcal{O})$を位相空間とする. $X$が連結であるとは, 開集合かつ閉集合である$X$の部分集合が全体集合$X$と空集合$\emptyset$のみであるということである.
これだけを見てもピンと来ないかもしれません。例を考えてみましょう。
$\mathbb{R}$に通常の位相を考えたものは、連結です。
点が2個以上からなる離散位相は連結ではありません。なぜなら任意の部分集合が開集合であり、閉集合だからです。
密着位相はいつでも連結です。看板に偽りなしです。
$\mathbb{R}$に通常の位相を考えたものは連結ですが、その部分集合に相対位相を考えたものは連結とは限りません。(相対位相はこちらのぼくの記事で!!!→
相対位相って何
)
たとえば$\mathbb{R}-\{0\}$に相対位相を考えると、これは連結ではありません!その位相における開集合かつ閉集合の部分集合は、全体と空集合のほかに 開区間$(-\infty,0), (0,+\infty)$があります。
まあ普通の連結性についてはこの例を知っていれば大丈夫な気がします。弧状連結とか弧連結とか色々考えて行くなら例として足りないので、興味がお有りでしたら位相空間における連結について調べてみてください!(弧連結 $\Longrightarrow$ 弧状連結 $\Longrightarrow$ 連結 が成立します!)
 アイキャッチ
アイキャッチ
さて、連結性について次が成立します。これが書きたかったものです。
$(X,\mathcal{O}_X), (Y,\mathcal{O}_Y)$を位相空間, $f:X \rightarrow Y$を連続写像とする.
このとき, 部分集合$A \subset X$に$X$の相対位相を入れたものが連結ならば, 部分集合$f(A) \subset Y$に$Y$の相対位相を入れたものも連結.
ではこれを使ってみましょう!
解き方5
問題文をもう一度貼っておきます。
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
$\mathbb{R}$は連結ですが、$f(\mathbb{R})=\{0,1\}$に相対位相を入れたものは連結ではありません!終わり!!!
中間値の定理
ここでは位相空間バージョンの中間値の定理を紹介します!なんと拡張があるんですね~
$(X,\mathcal{O})$を連結な位相空間, $f:X \rightarrow \mathbb{R}$を連続関数, $x_1,x_2$を$f(x_1) < f(x_2)$を満たす$X$の点とする. また$\alpha = f(x_1), \beta = f(x_2)$としておく.($\alpha < \beta$が成立している.)
このとき$\alpha < \gamma < \beta$となる$\gamma$について, $f(x) = \gamma$となる$X$の点$x$が存在する.
証明は書きませんが、頑張れば自力で証明できるくらいの感じなので、一度やってみるといいかもしれません!
解き方6
まあ、あの、お気づきの方はいると思うのですが位相空間版の中間値の定理を説明する必要って全く無かったんですよね 実数関数の場合って別に 初等的な解析学としてみなさんすでに学んでいると思いますし 説明したかったので書きました(真顔)
問題文をもう一度貼っておきます。
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
では解き方6です。$f$が連続であるとすると、$\mathbb{R}$が連結なので中間値の定理が使えます。つまり$0<1/2<1$より$f(x)=1/2$となる$x$が存在するはずです。矛盾!!!ゲームセット!!!勝負あり!!!フルタイム!!!ノーサイド!!!
稠密な部分集合とは
ま、まだやるか!? 作ろうと思えばまだ別解を作れそうですが、私が好きな定理を用いる証明で締めくくろうと思います。では稠密の定義から。
$(X,\mathcal{O}_X)$を位相空間とするとき, 部分集合$A \subset X$が稠密であるとは, $\overline{A} = X$が成立することをいう。
超有名な例を書いておきます。
通常の位相を考えた$\mathbb{R}$の部分集合$\mathbb{Q}$は稠密な部分集合になります。
このような、高々可算な稠密部分集合をもつ位相空間を可分空間と呼んだりします。
「稠」の字にまつわる余談
「稠」の字のつくりは「周」ではない、という言説があります。よく見ると「土」の下にまで線が突き出ています。ですが、「周」で書いたとしても「同じ字種の別の書き方」でしかないのでこれは「間違い」ではありません。漢検でも◯になります。以上余談でした。
 チョウと読むときもある
チョウと読むときもある
好きな定理を紹介
さて、好きな定理を紹介します!!!それは次の主張になります。
$f,g$を位相空間$(X,\mathcal{O}_X)$上の実連続関数, $D$を$X$の稠密な部分集合とする.
このとき, $D$の任意の点$x$において$f(x)=g(x)$が成立するなら$f=g$となる.
驚きの定理です。まあでも納得感はありますよね。さっきの例で言えば、有理数全体で等しい実連続関数は実数全体でも等しいということです。
解き方7
問題文をもう一度貼っておきます。
$\mathbb{R}$上の関数$f:\mathbb{R} \rightarrow \mathbb{R}$を、$f(0)=1, f(x)=0$ $(x \ne 0)$で定める. このとき$f$は連続関数でないことを示せ.
それではこの定理を使ってみます!!!$\mathbb{R}$において$D=\mathbb{R}-\{0\}$は稠密な部分集合です。このとき$D$の上で$f$と、つねに$0$をとる定数関数は同じ値を取ります。ですが実際は異なる関数です。これは$f$が連続関数でないことを意味します!!!
終わりに
ここまで読んでいただきありがとうございます。位相空間の基本を身につける勉強というのは大変だと思います。抽象的ですし、面白い講義を行うのも難しい分野なのだと思います。そもそも位相空間を楽しんで学べる人などいるのか?とすら思ってしまうかもしれません。
当時の私も位相空間の基本的な事項を学ぶのは辛かったです。ですが特徴的な具体例について考えたり、解析学で証明したものが位相空間のレベルに拡張できる例に触れたりなど、おもしろ情報の存在に助けられて位相空間を好きになることができました。(位相空間に触れてから好きになるまで3年くらいかかってますが。)
この記事はそういうおもしろコラムをつまみ食いできるテーマとして、連続でない関数を選んで書いてみた、というものになります。この記事を通して位相空間を「楽しい分野」と捉えることができた人が一人でも増えることを願っています。
(思わず真面目に文章を書いてしまいました もし面白かったという方は記事の高評価お願いします! それでは~~~)
