デデキント・マクニール完備化
Wikipediaを眺めていたら
デデキント・マクニール完備化
(Dedekind-MacNeille completion) という概念を知ったので,勉強したことを書き残しておきます.
デデキント・マクニール完備化とは,半順序集合に対して,それを含む最小の完備束を構成する操作のことです.
上の画像が何をしているのかイメージできるようになることを目標に解説していきます.
詳しくは後述しますが,デデキント・マクニール完備化は冪集合の部分集合として構成されます.
![半順序集合!FORMULA[0][37205][0]を,冪集合!FORMULA[1][754177012][0]に含まれるある完備束!FORMULA[2][1329949504][0]に埋め込む](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FPOczfBLCsP6wyTdKl2b1.jpeg?alt=media) 半順序集合$S$を,冪集合$\powerset{S}$に含まれるある完備束$\dm{S}$に埋め込む
半順序集合$S$を,冪集合$\powerset{S}$に含まれるある完備束$\dm{S}$に埋め込む
準備
上界・下界
$S$を半順序集合とし,$A$を$S$の部分集合とする.
このとき$A$の上界全体の集合を$\upper{A}$と書き,$A$の下界全体の集合を$\lower{A}$と書く.
\begin{align*}
\upper{A}&:=\{u\in S\mid \text{任意の $a\in A$ に対して $a\le u$ が成り立つ}\}, \\
\lower{A}&:=\{l\in S\mid \text{任意の $a\in A$ に対して $l\le a$ が成り立つ}\}.
\end{align*}
$(S,\le)$を半順序集合とし,$x,y\in S$とする.このとき,次の3条件は同値である.
- $x\le y$.
- $\lower{\{x\}}\subset\lower{\{y\}}$.
- $\upper{\{x\}}\supset\upper{\{y\}}$.
- $(\Rightarrow)$:$z\in\lower{\{x\}}$を任意に取ると,$z\le x\le y$より$z\in\lower{\{y\}}$が成り立つ.
- $(\Leftarrow)$:反射律より$x\in\lower{\{x\}}\subset\lower{\{y\}}$となるから$x\le y$である.
$(S,\le)$を半順序集合とし,$A,B$を$S$の部分集合とする.このとき,次のことが成り立つ.
- $A\subset \dmcl{A}$と$A\subset A^{\mathrm{lu}}$が成り立つ.
- $A\subset B$であれば,$\upper{A}\supset\upper{B}$と$\lower{A}\supset\lower{B}$が成り立つ.
- $A\subset B$であれば,$\dmcl{A}\subset\dmcl{B}$と$A^{\mathrm{lu}}\subset B^{\mathrm{lu}}$が成り立つ.
- $A^{\mathrm{ulu}}=\upper{A}$と$A^{\mathrm{lul}}=\lower{A}$が成り立つ.
- $a\in A$を任意に取る.このとき任意の$u\in\upper{A}$に対して$a\le u$が成り立つから,$a$は$\upper{A}$の下界であり$a\in\dmcl{A}$を得る.同様に,任意の$l\in\lower{A}$に対して$l\le a$が成り立つから,$a$は$\lower{A}$の上界であり$a\in A^{\mathrm{lu}}$も成り立つ.
- $u\in\upper{B}$と$a\in A$を任意に取ると,$A\subset B$より$a\in B$だから$a\le u$が成り立ち,$u\in\upper{A}$を得る.$\lower{A}\supset\lower{B}$も同様に示せる.
- (2)より$\upper{A}\supset\upper{B}$が成り立つから,再び(2)を使えば$\dmcl{A}\subset\dmcl{B}$を得る.$A^{\mathrm{lu}}\subset B^{\mathrm{lu}}$も同様に示せる.
- (1)より$A\subset \dmcl{A}$が成り立つから,(2)より$\upper{A}\supset A^{\mathrm{ulu}}$である.また,(1)より$\upper{A}\subset A^{\mathrm{ulu}}$でもある.$A^{\mathrm{lul}}=\lower{A}$も同様に示せる.
特に次の3性質が成り立つことに注意しておきます.
- $A\subset\dmcl{A}$である.
- $A\subset B$ならば,$\dmcl{A}\subset\dmcl{B}$である.
- $\dmcl{(\dmcl{A})}=\dmcl{A}$である.
前命題 (1),(2) より${\upper{(\,\cdot\,)}}:\powerset{X}\rightleftarrows\powerset{X}:{\lower{(\,\cdot\,)}}$は
Galois接続
である.
(4) が成り立つことや$A\mapsto\dmcl{A}$が閉包作用素となること(に対応する主張)は,一般のGalois接続に対しても全く同様に示される.
$\dmcl{\emptyset}=\emptyset$を満たさない半順序集合$S$の例を一つ挙げよ.
$\upper{\emptyset}=S$だから,最小元をもつ半順序集合を考えればよい.たとえば大小関係による半順序集合$\mathbb{N}$は$0$を最小元にもつから
$$ \dmcl{\emptyset}=\lower{\mathbb{N}}=\{0\}$$
である.
完備束
任意の部分集合が上限と下限をもつような半順序集合を 完備束 といいますが,この定義は「次の2条件 (1), (2) のどちらか一方を満たすこと」と弱めることができます.
半順序集合$S$について,次の2条件は同値である.
- $S$の任意の部分集合が上限をもつ.
- $S$の任意の部分集合が下限をもつ.
$S$の任意の部分集合$A$に対して,下記2点より$\sup_{S}(\lower{A})$が$A$の下限となる.
- $\sup_{S}(\lower{A})=\min(A^{\mathrm{lu}})$と$A^{\mathrm{lu}}\supset A$より,$\sup_{S}(\lower{A})$は$A$の下界である.
- $A$の下界$x\in S$を任意に取ると,$x\in\lower{A}$より$x\le \sup_{S}(\lower{A})$が成り立つ.
この証明から,次のこともわかります.
完備束$L$とその部分集合$A$に対して,$\sup_L(A)=\inf_L(\upper{A})$と$\inf_L(A)=\sup_L(\lower{A})$が成り立つ.
順序埋め込み
半順序集合$S,L$と写像$\iota:S\to L$を考える.
- $\iota$が単調増加であるとは,$x\le y$を満たす任意の$x,y\in S$に対して$\iota(x)\le\iota(y)$が成り立つことをいう.
- $\iota$が順序を反映するとは,$\iota(x)\le \iota(y)$を満たす任意の$x,y\in S$に対して$x\le y$が成り立つことをいう.
- $\iota$が順序埋め込みであるとは,$\iota$が単調増加かつ順序を反映することをいう.
半順序集合$S,L$と順序を反映する写像$\iota:S\to L$について,$\iota$は単射である.
$x,y\in S$が$\iota(x)=\iota(y)$を満たすとき,反射律より$\iota(x)\le\iota(y)$かつ$\iota(x)\ge\iota(y)$が成り立つ.すると$\iota$が順序を反映することから$x\le y$かつ$x\ge y$となり,反対称律より$x=y$を得る.
デデキント・マクニール完備化
定義と最小性
デデキント・マクニール完備化の定義を述べる前に,次の命題を示しておきます.
$L$を完備束とし,写像$\operatorname{Cl}:L\ni x\mapsto x^{\ast}\in L$は次の3条件を満たすとする.
- 任意の$x\in L$に対して,$x\le x^{\ast}$が成り立つ.
- $x\le y$を満たす任意の$x,y\in L$に対して,$x^{\ast}\le y^{\ast}$が成り立つ.
- 任意の$x\in L$に対して,$x^{\ast\ast}\le x^{\ast}$が成り立つ.
このとき,次のことが成り立つ.
- 任意の$x\in L$に対して,$x^{\ast\ast}=x^{\ast}$が成り立つ.
- $\pushout{\operatorname{Cl}}(L)=\{x\in L\mid x^{\ast}=x\}$である.(ただし,$\pushout{\operatorname{Cl}}(L)$は$\operatorname{Cl}$による$L$の像とした.(矢印記法))
- $\pushout{\operatorname{Cl}}(L)$の部分集合$S$に対して,($\pushout{\operatorname{Cl}}(L)$における)$S$の上限・下限がともに存在して
\begin{align*} \sup\nolimits_{\pushout{\operatorname{Cl}}(L)}(S)&=\sup\nolimits_{L}(S)^{\ast}, \\ \inf\nolimits_{\pushout{\operatorname{Cl}}(L)}(S)&=\inf\nolimits_{L}(S) \end{align*}
が成り立つ.よって,$\pushout{\operatorname{Cl}}(L)$は($L$の半順序部分集合として)完備束である.
- 条件1より$x\le x^{\ast}$だから,条件2より$x^{\ast}\le x^{\ast\ast}$となる.これと条件3を合わせればよい.
- 任意の$x\in\pushout{\operatorname{Cl}}(L)$に対して,$x=y^{\ast}$を満たす$y\in L$を取れば$x^{\ast}=y^{\ast\ast}=y^{\ast}=x$となる.逆の包含は明らか.
- まず上限について,任意の$x\in S$に対して
$$ x\le\sup\nolimits_L(S)\le\sup\nolimits_L(S)^{\ast}$$
が成り立つから,$\sup\nolimits_L(S)^{\ast}$は$S$の上界である.また$S$の上界$u\in\pushout{\operatorname{Cl}}(L)$を任意に取ると,$\sup_L(S)\le u$より
$$ \sup\nolimits_L(S)^{\ast}\le u^{\ast}=u$$
が成り立つから,$\sup\nolimits_L(S)^{\ast}$は$S$の上界の最小元であり$\sup_{\pushout{\operatorname{Cl}}(L)}(S)=\sup_{L}(S)^{\ast}$を得る.
下限については,$\inf_{L}(S)\in\pushout{\operatorname{Cl}}(L)$であることを示せばよい.任意の$x\in S$に対して,$\inf_{L}(S)\le x$より$\inf_{L}(S)^{\ast}\le x^{\ast}=x$が成り立つ($x\in S\subset\pushout{\operatorname{Cl}}(L)$に注意).よって$\inf_{L}(S)^{\ast}$は$L$における$S$の下界だから$\inf_{L}(S)^{\ast}\le \inf_{L}(S)$を得る.
$L=\powerset{S}$,$\operatorname{Cl}(A)=\dmcl{A}$に対して上の命題を使えば,次の完備束$\dm{S}$が得られます.
半順序集合$S$に対して,そのデデキント・マクニール完備化$\dm{S}$を
$$ \dm{S}:=\{A\in\powerset{S}\mid \dmcl{A}=A\}$$
で定める.
半順序集合$S$のデデキント・マクニール完備化$\dm{S}$は(包含関係に関して)完備束である.
前命題から従う.
半順序集合$S$は,そのデデキント・マクニール完備化$\dm{S}$に埋め込むことができます.
つまり,$x\in S$と$\lower{\{x\}}\in\dm{S}$を同一視することによって,$S$を$\dm{S}$の半順序部分集合とみなせます.
$S$を半順序集合とし,各$x\in S$に対して$\iota(x):=\lower{\{x\}}$とおく.
- 任意の$x\in S$に対して,$\iota(x)\in\dm{S}$が成り立つ.
- 写像$\iota:S\to\dm{S}$は順序埋め込みである.
- 既に示した通り$\lower{\{x\}}=\{x\}^{\mathrm{lul}}$が成り立つから,$\iota(x)=\dmcl{\iota(x)}$である.
- 既に示した通り,$x,y\in S$について$x\le y$であることと$\lower{\{x\}}\subset\lower{\{y\}}$であることは同値である.
またデデキント・マクニール完備化$\dm{S}$は,次の意味で$S$を含む最小の完備束になっています.
半順序集合$S$と完備束$L$および順序埋め込み$j:S\to L$に対して,$j=j'\circ\iota$を満たす順序埋め込み$j':\dm{S}\to L$が存在する.
写像$j':\dm{S}\ni A\mapsto \sup_{L}(\pushout{j}(A))\in L$が所望の性質を満たすことを確認する.まず任意の$x\in S$に対して,下記2点より$j(x)=(j'\circ \iota)(x)$が成り立つ.
- 任意の$y\in\iota(x)$に対して$y\le x$より$j(y)\le j(x)$が成り立つから,$j(x)$は$\pushout{j}(\iota(x))$の上界である.
- 反射律$x\in\iota(x)$より$j(x)\in\pushout{j}(\iota(x))$であることを踏まえると,$\pushout{j}(\iota(x))$の任意の上界$u\in L$に対して$j(x)\le u$が成り立つ.
また,下記2点より$j'$は順序埋め込みである.
- $A,B\in\dm{S}$が$A\subset B$を満たすとき,$\pushout{j}(A)\subset\pushout{j}(B)$より$j'(A)\le j'(B)$である.
- $A,B\in\dm{S}$が$j'(A)\le j'(B)$を満たすとし,$a\in A$と$u\in\upper{B}$を任意に取る.このとき$j$の単調増加性より$j(u)$は$\pushout{j}(B)$の上界となるので
$$ j(a)\le \sup\nolimits_{L}(\pushout{j}(A))=j'(A)\le j'(B) =\inf\nolimits_{L}(\upper{\pushout{j}(B)})\le j(u)$$
より$a\le u$が成り立ち,$a\in \dmcl{B}=B$である.
半順序集合$S$とその部分集合$A\in\dm{S}$に対して
$$ A=\bigcup\pushout{\iota}(A)=\bigcap \pushout{\iota}(\upper{A}) $$
が成り立つことを示せ.
次の2式を示せば十分.
$A\subset\bigcup\pushout{\iota}(A)\subset\dmcl{A}$.
$a\in A$のとき,反射律より$a\in\iota(a)$が成り立つから$$ a\in \bigcup\{\iota(a')\mid a'\in A\}=\bigcup\pushout{\iota}(A)$$である.また$x\in\bigcup\pushout{\iota}(A)$のとき,$x\in\iota(a)$を満たす$a\in A$が存在する.このとき任意の$u\in\upper{A}$に対して$x\le a\le u$が成り立つから,$x\in\dmcl{A}$となる.
$A\subset\bigcap \pushout{\iota}(\upper{A})\subset\dmcl{A}$.
$a\in A$のとき,任意の$u\in\upper{A}$に対して$a\le u$より$a\in\iota(u)$が成り立つから
$$ a\in \bigcap\{\iota(u)\mid u\in\upper{A}\}=\bigcap\pushout{\iota}(\upper{A})$$
である.また$x\in\bigcap\pushout{\iota}(\upper{A})$のとき,任意の$u\in\upper{A}$に対して$x\in\iota(u)$より$x\le u$が成り立つから,$x\in\dmcl{A}$となる.
$S,T$を半順序集合とし,$f:S\to T$を単調増加写像とする.このとき,ある単調増加写像$\dm{f}:\dm{S}\to\dm{T}$が存在して,任意の$x\in S$に対して
$$ \dm{f}(\{s\in S\mid s\le x\})=\{t\in T\mid t\le f(x)\}$$
が成り立つことを示せ.
解答例
(デデキント・マクニール完備化の最小性の証明で「$j$が順序を反映すること」は「$j'$が順序を反映すること」を示すためにしか使わなかったことに注意して,$j=\iota_T\circ f$に対して同じ議論をすればよい.)
$\iota_S:S\ni x\mapsto\{s\in S\mid s\le x\}\in\dm{S}$,$\iota_T:T\ni y\mapsto\{t\in T\mid t\le y\}\in\dm{T}$とし,
$$ \dm{f}(A):=\sup\nolimits_{\dm{T}}(\pushout{(\iota_T\circ f)}(A))$$
で定める写像$\dm{f}:\dm{S}\to\dm{T}$が所望の性質を満たすことを確認する.
- $x\in S$を任意に取る.このとき任意の$s\in\iota_S(x)$に対して
$$ (\iota_T\circ f)(s)\le(\iota_T\circ f)(x)$$
が成り立つことに注意すれば
\begin{align*} \dm{f}(\iota_S(x)) &=\sup\nolimits_{\dm{T}}(\pushout{(\iota_T\circ f)}(\iota_S(x))) \\ &=(\iota_T\circ f)(x). \end{align*} - $A\subset B$を満たす$A,B\in\dm{S}$を任意に取る.このとき
$$ \pushout{(\iota_T\circ f)}(A)\subset\pushout{(\iota_T\circ f)}(B)$$
より$\dm{f}(A)\subset\dm{f}(B)$を得る.
例
$\dm{\mathbb{N}}$は$\mathbb{N}\cup\{\infty\}$と順序同型である.($\mathbb{Q},\mathbb{N}\cup\{\infty\}$は大小関係によって全順序集合とみなしている)
$\mathbb{N}$の部分集合$A$に対して,次のことが成り立つ.
- $A$が上に有界である場合:$\upper{A}$の最小元$n$が存在して$\dmcl{A}=\{0,1,\ldots,n\}$が成り立つ.
- $A$が上に有界でない場合:$\dmcl{A}=\lower{\emptyset}=\mathbb{N}$が成り立つ.
したがって$\dm{\mathbb{N}}=\{\{0,1,\ldots,n\}\mid n\in\mathbb{N}\}\cup\{\mathbb{N}\}$である.すると,次の写像$j:\mathbb{N}\cup\{\infty\}\to\dm{\mathbb{N}}$は明らかに順序同型である.
$$ j(n):=\begin{cases}\{0,1,\ldots,n\} & (n\in\mathbb{N}),\\\mathbb{N} & (n=\infty).\end{cases}$$
$\dm{\mathbb{Q}}$は$\overline{\mathbb{R}}=\mathbb{R}\cup\{-\infty,\infty\}$と順序同型である.($\mathbb{Q},\overline{\mathbb{R}}$は大小関係によって全順序集合とみなしている)
順序埋め込み$\iota:\mathbb{Q}\ni x\mapsto(-\infty,x]\cap\mathbb{Q}\in\dm{\mathbb{Q}}$と包含写像$j:\mathbb{Q}\to\overline{\mathbb{R}}$に対して,$j=j'\circ\iota$を満たす順序埋め込み$j':\dm{\mathbb{Q}}\to\overline{\mathbb{R}}$が存在し,この$j'$の全射性が次のように示せる.
- $y\in\mathbb{R}$を任意に取り,$A:=(-\infty,y]\cap\mathbb{Q}$とおく.このとき$\mathbb{Q}$の稠密性より
$$ \dmcl{A}=\lower{([y,\infty)\cap\mathbb{Q})}=(-\infty,y]\cap\mathbb{Q}=A$$
が成り立つから,$A\in\dm{\mathbb{Q}}$であり拡大実数$j'(A)\in\overline{\mathbb{R}}$を考えることができる.$y=j'(A)$を示すため$\varepsilon\in(0,\infty)$を任意に取ると,$y-\varepsilon< x_{-}\le y\le x_{+}< y+\varepsilon$を満たす有理数$x_{-},x_{+}\in\mathbb{Q}$が存在し,$j'$が順序埋め込みであることから
$$ y-\varepsilon< x_{-}=j'((-\infty,x_{-}]\cap\mathbb{Q})\le j'(A)\le j'((-\infty,x_{+}]\cap\mathbb{Q})=x_{+}< y+\varepsilon$$
が成り立つ.よって$\varepsilon$の任意性より$y=j'(A)$を得る. - $\dmcl{\emptyset}=\lower{\mathbb{Q}}=\emptyset$より$\emptyset\in\dm{\mathbb{Q}}$であることに注意すると,拡大実数$j'(\emptyset)\in\overline{\mathbb{R}}$を考えることができる.ところで$j'$は順序埋め込みだから,任意の有理数$x\in\mathbb{Q}$に対して
$$ x=j(x)=j'((-\infty,x]\cap\mathbb{Q})\ge j'(\emptyset)$$
が成り立ち,$j'(\emptyset)=-\infty$を得る.同様にして$j'(\mathbb{Q})=\infty$も成り立つ.
他にも簡単な例をいくつか挙げておきます.
(どのような半順序を考えているか説明するのは大変なので,ハッセ図で済ませます.)
 デデキント・マクニール完備化によって最大元と最小元が増えた
デデキント・マクニール完備化によって最大元と最小元が増えた
2個以上の元をもつ集合$S$を等号$=$によって半順序集合とみなす.このとき,デデキント・マクニール完備化$\dm{S}$は$S\cup\{\perp,\top\}$と順序同型であることを示せ.ただし,${\perp},{\top}$は$S$に属さないある元であり,$S\cup\{\perp,\top\}$は次の半順序
$$ x\le y\iff \text{$x={\perp}$ または $y={\top}$ または $x=y$}$$
によって$S$を含む半順序集合とみなしている.
解答例
$S$の部分集合$A$について,次のことが成り立つ.
- $A=\emptyset$のとき,$\dmcl{A}=\lower{S}=\emptyset$である.
- $\#A=1$のとき,$\dmcl{A}=\lower{A}=A$である.
- $\#A\ge 2$のとき,$\dmcl{A}=\lower{\emptyset}=S$である.
$$ j(x):=\begin{cases}\emptyset&(x={\perp}),\\\{x\}&(x\in S),\\S&(x={\top}).\end{cases}$$
有限全順序集合$S$は完備束だから,そのデデキント・マクニール完備化$\dm{S}$は$S$と順序同型である.
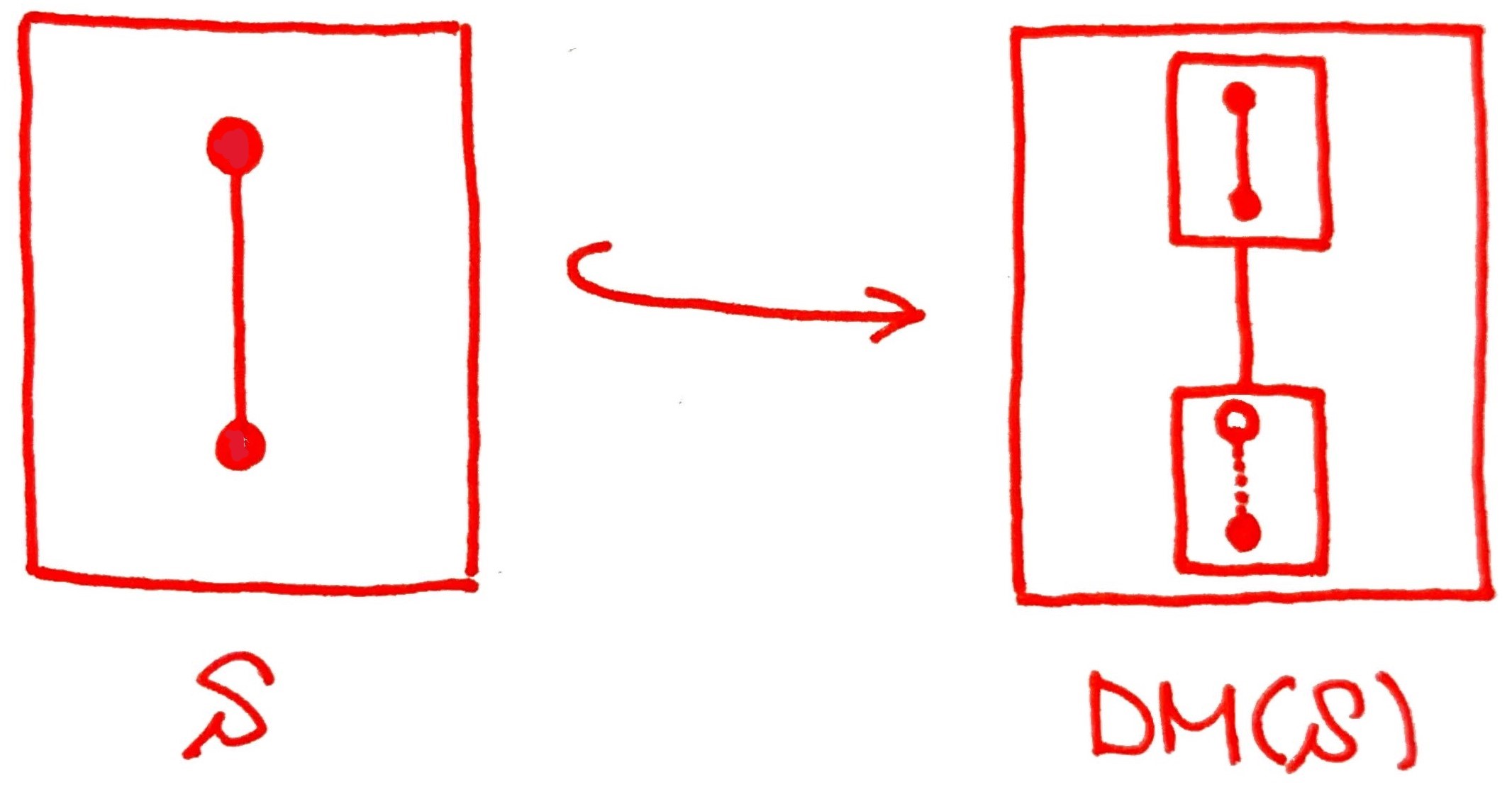 デデキント・マクニール完備化しても変わらない(その1)
デデキント・マクニール完備化しても変わらない(その1)
 デデキント・マクニール完備化しても変わらない(その2)
デデキント・マクニール完備化しても変わらない(その2)
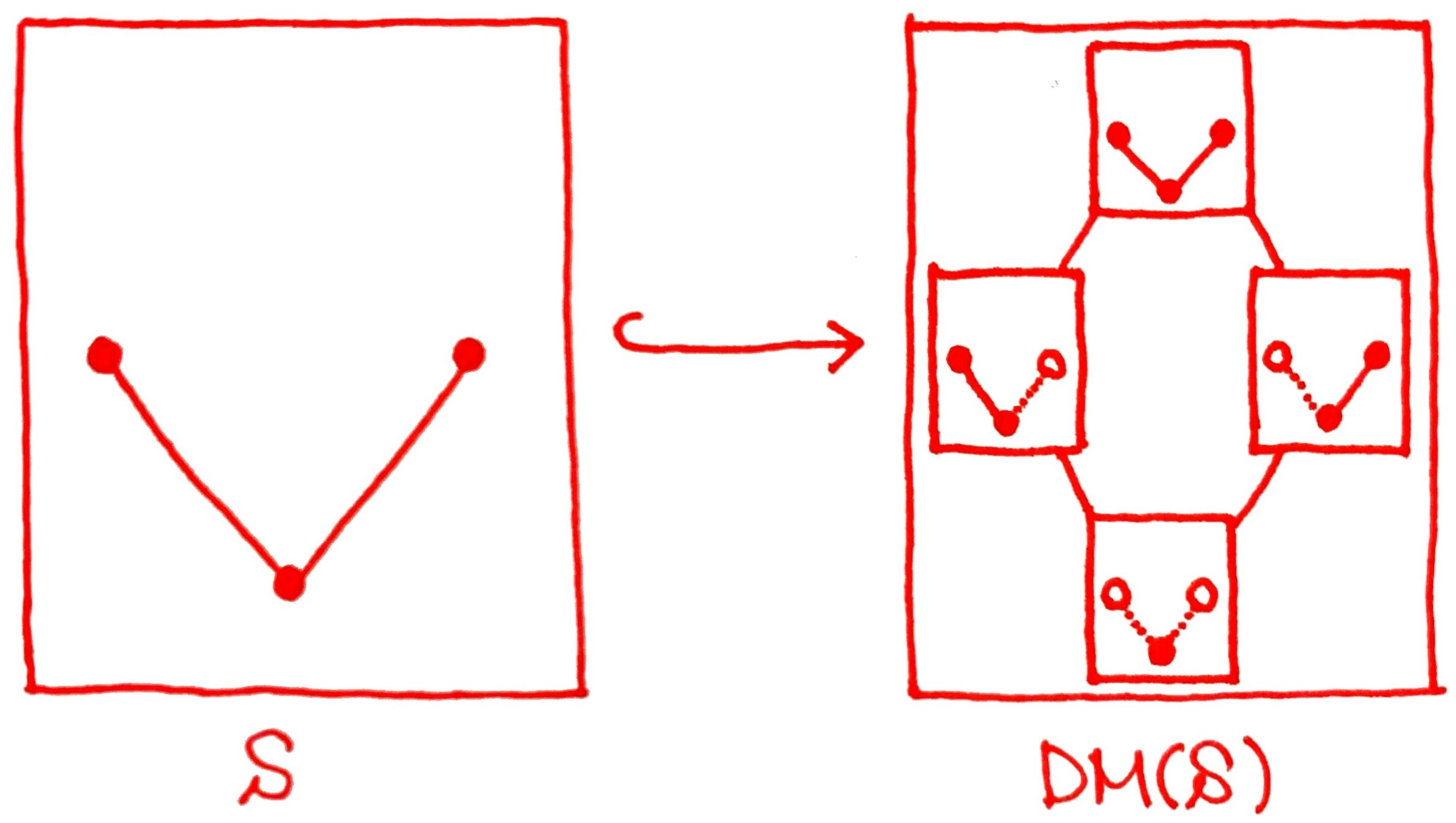 デデキント・マクニール完備化によって最大元が増えた
デデキント・マクニール完備化によって最大元が増えた
 デデキント・マクニール完備化によって最小元が増えた
デデキント・マクニール完備化によって最小元が増えた
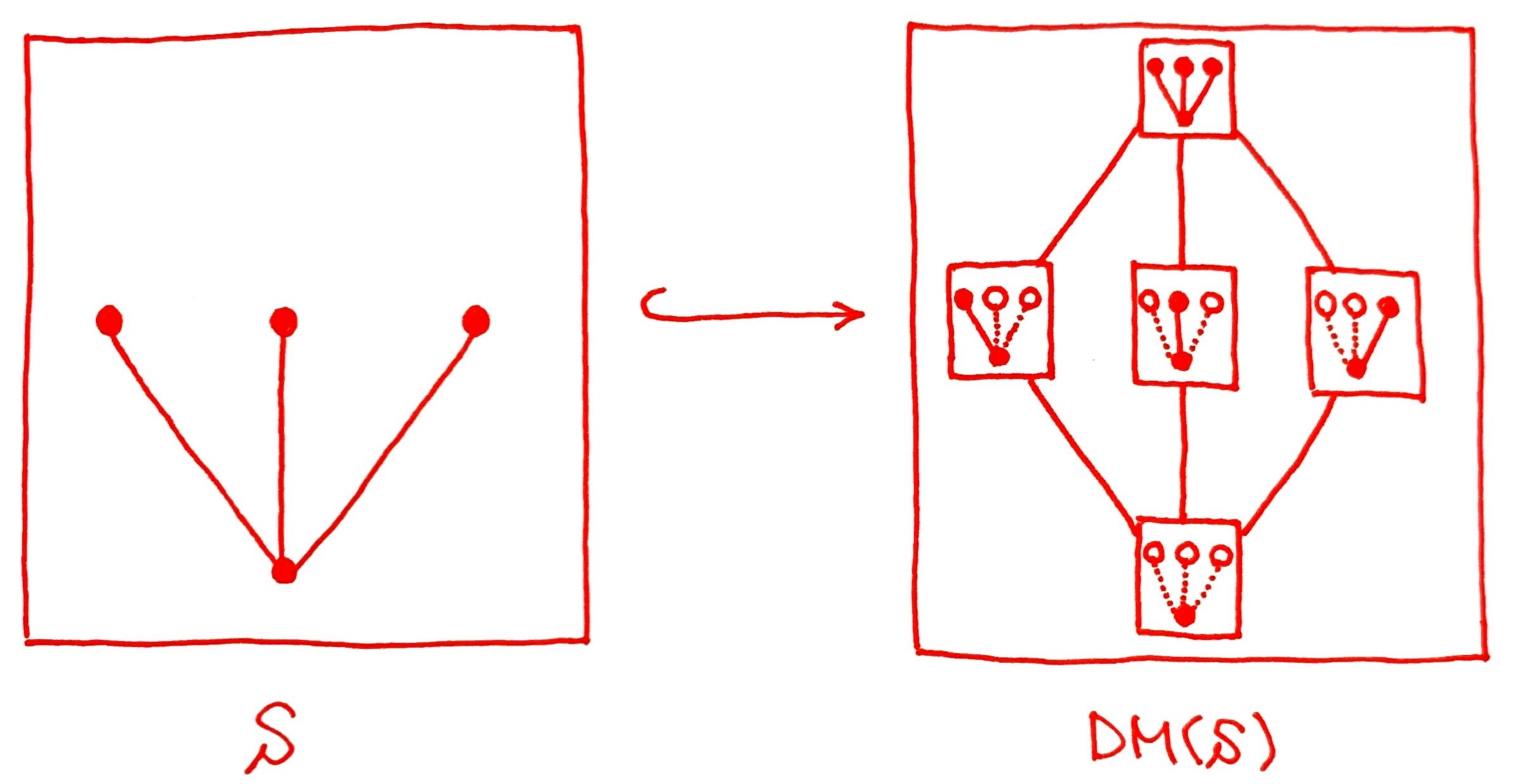 デデキント・マクニール完備化によって最大元が増えた
デデキント・マクニール完備化によって最大元が増えた
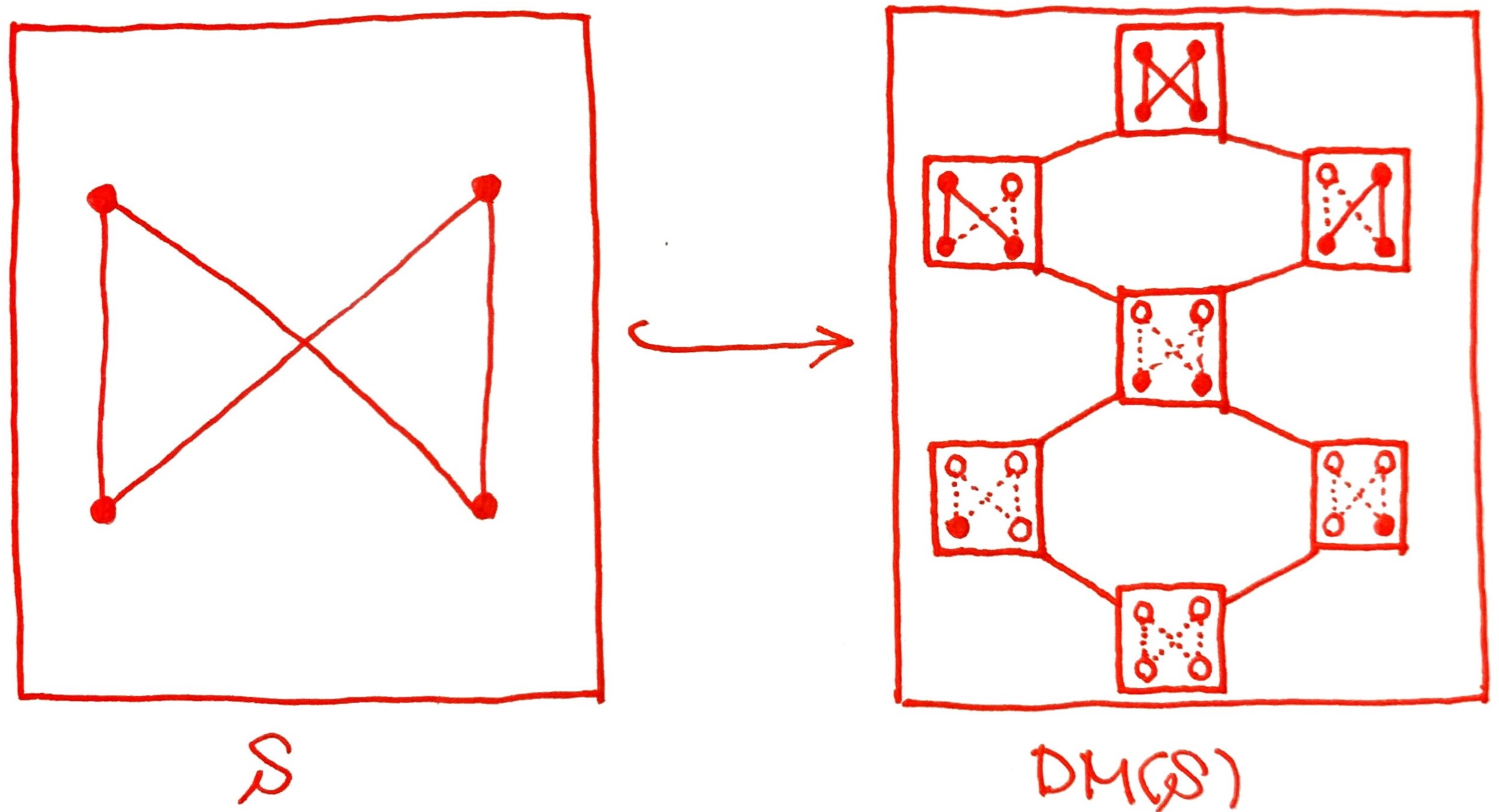 デデキント・マクニール完備化によって3つの元が増えた
デデキント・マクニール完備化によって3つの元が増えた
$4$点からなる次の半順序集合に対して,そのデデキント・マクニール完備化のハッセ図を描け.
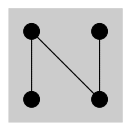 N字のハッセ図
N字のハッセ図
解答例
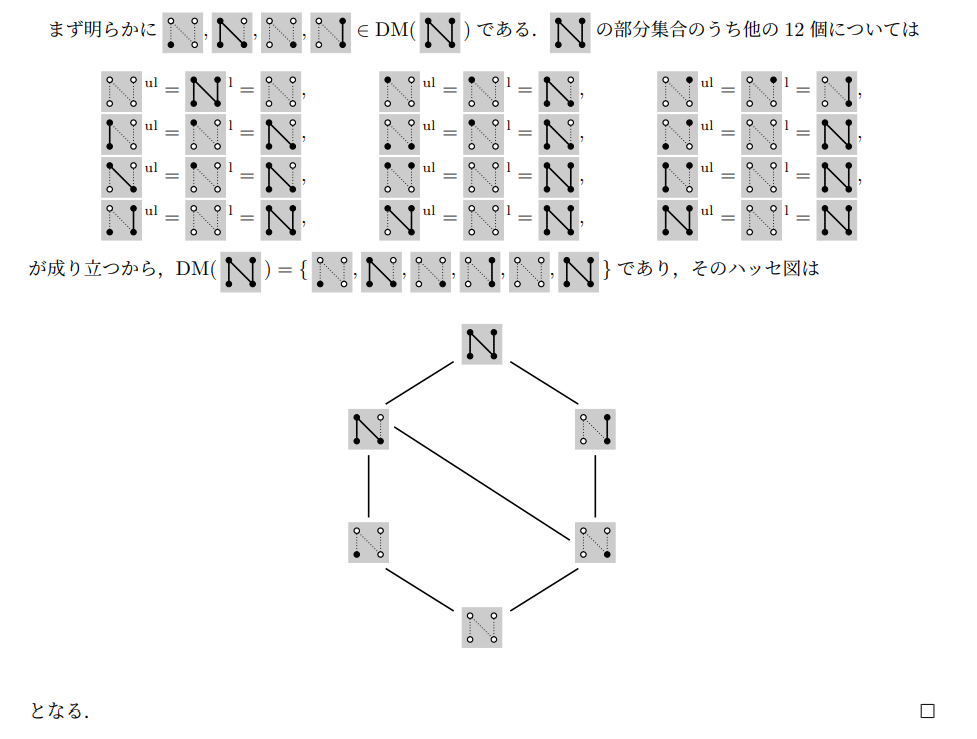 解答例
解答例
誤りがあればご指摘いただけると幸いです.
ここまでお読みいただきありがとうございました.
に載っていた[画像](https://commons.wikimedia.org/wiki/File:Dedekind-Macneille_completion.svg)](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FXAh8Qzq5cGvKCKcEOwZF.png?alt=media)
